nDNA v2 — Tensor-Rich Belief Torsion
While our current framework encapsulates belief as a vector-valued semantic steering force, it is possible to extend this formulation to a richer tensor-based representation of belief.
This higher-order representation $\mathbf{T}_\ell^{(c)} \in \mathbb{R}^{d \times d \times \cdots}$ captures complex multi-dimensional interactions within the latent activation space, enabling the modeling of nonlinear dependencies, higher-order correlations, and contextual entanglements that are fundamentally inaccessible to vector embeddings alone. By encoding semantic torsion, curvature, and multi-modal interactions across layers, tensor-based belief representation offers a powerful framework to characterize subtle latent geometry and richer internal dynamics of language models.
Such a tensor-rich approach is particularly beneficial in cases involving multimodal fusion, hierarchical reasoning, and complex compositionality, where simple vectorial steering fails to capture intertwined semantic constraints and latent contextual shifts. For example, in tasks demanding disentanglement of overlapping concepts or fine-grained alignment of multi-turn dialogue states, tensors can explicitly encode relational structure and layered semantic dependencies.
However, this expressivity comes with a significant computational overhead, as tensor operations increase dimensionality exponentially and necessitate efficient approximation schemes or structured sparsity to remain scalable. Balancing the tradeoff between modeling fidelity and computational tractability is a central challenge we are actively addressing in ongoing research, with promising directions including low-rank tensor decompositions and hybrid vector-tensor architectures.
In summary, while belief-as-tensor unlocks richer representational nuance and deeper semantic insight, its practical deployment requires careful design to harness its power without prohibitive costs—we are currently working.
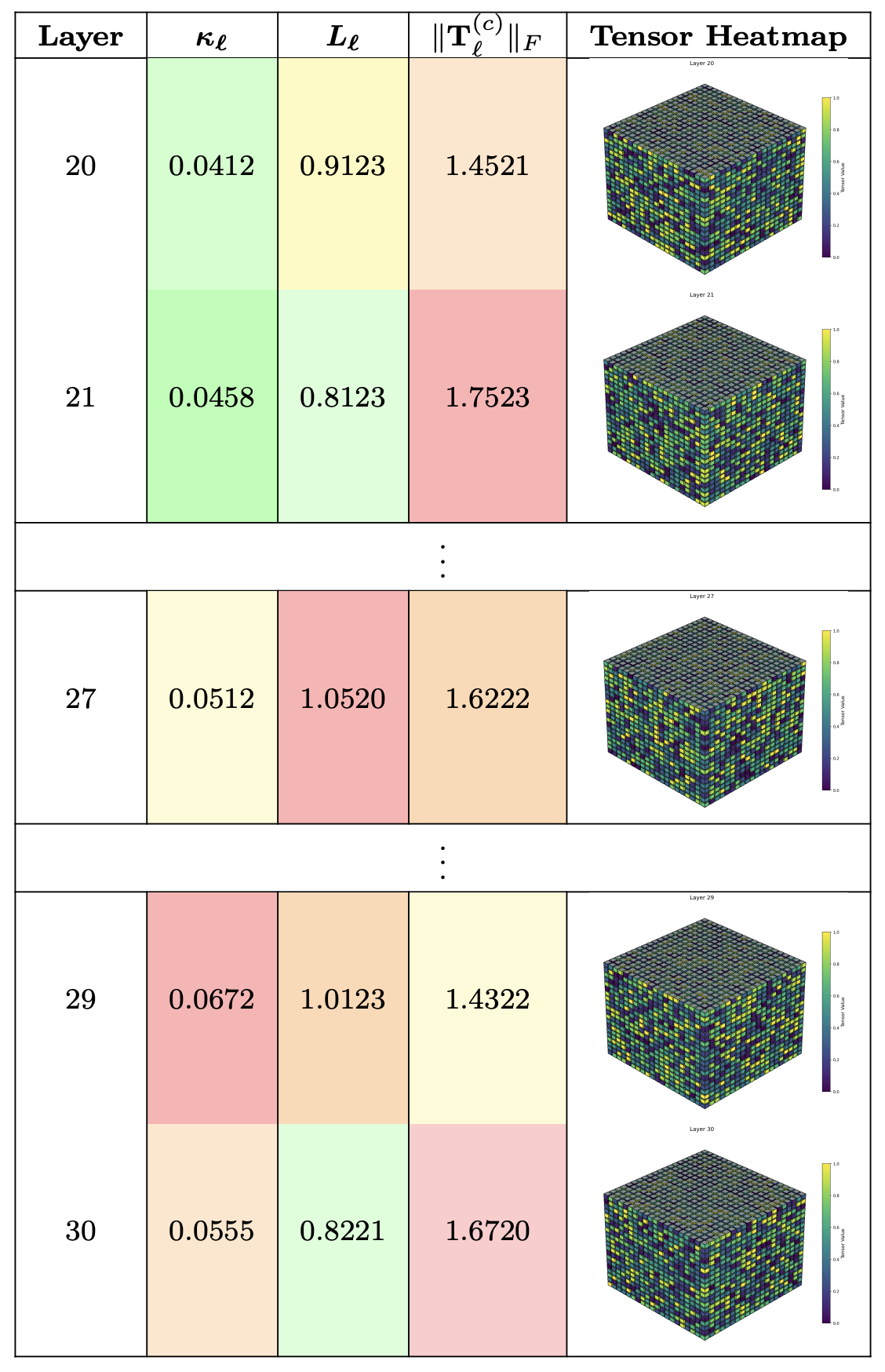
Illustrative nDNA Tensor Example: Presents a combined view of spectral curvature $\kappa_\ell$, thermodynamic length $\mathcal{S}_\ell$, Frobenius norm of tensor slices $|\mathbf{T}_\ell^{(c)}|_F$, alongside visual heatmaps of the corresponding tensor, highlighting the intricate latent geometry at different layers.