Lens - Quantization and Pruning as Thermodynamic Collapses

What do quantization and pruning do to a model’s epistemic structure beyond reducing FLOPs and memory? Can we understand them not merely as engineering shortcuts, but as belief geometry events that alter the latent semantics of a model’s neural genome?

In this section, we pose a central research question:
How do quantization and pruning reshape the model’s internal belief geometry–specifically its spectral curvature, thermodynamic length, and belief vector field—when observed through the lens of neural DNA (nDNA) diagnostics?

While prior work often focuses on compression-induced accuracy trade-offs [1] [2] [3], quantization noise [4] [5], and robustness degradation [6] [7], we explore a deeper hypothesis: that such operations induce an irreversible semantic compression–analogous to an entropy collapse [8]–which distorts the model’s epistemic manifold and reduces its ability to preserve instructional, cultural, or conceptual diversity in reasoning [9] [10].

By visualizing nDNA geometry before and after quantization or pruning, we aim to reveal whether these methods disproportionately collapse high-torsion belief zones [11], thereby flattening semantic diversity into brittle, low-entropy attractors [12].

Our goal is to characterize these effects not simply as degradations in performance, but as geometric distortions in the latent epistemology of the model–illuminating what is truly lost when we squeeze too tightly.

nDNA as a Lens: Quantization and Pruning as Thermodynamic Collapses

Quantization as Thermodynamic Collapse. Quantization compresses weight precision (e.g., 4-bit or 2-bit representations [13] [14]), but also contracts the latent geometry. Through nDNA lens, this manifests as:

A contraction of thermodynamic length $\mathcal{L}_\ell$, reflecting diminished epistemic effort at layer $\ell$.
A flattening of spectral curvature $\kappa_\ell$, reducing representational richness and alignment adaptability.
A weakening of belief vector fields $\|\mathbf{v}_\ell^{(c)}\|$, implying reduced alignment steering capacity.

The collapse can be formalized as:

\[\boxed{ \mathcal{M}_{\text{full}} \xrightarrow{\text{quantization}} \mathcal{M}_{\text{compressed}} \quad \text{s.t.} \quad \mathcal{L}_\ell \downarrow,\; \kappa_\ell \downarrow,\; \|\mathbf{v}_\ell^{(c)}\| \downarrow }\]

As shown in the quantization analysis, the post-quantization trajectories across 9 culturally fine-tuned LLaMA variants reveal:

\[\mathcal{L}_\ell^{\text{pre}} \in [0.70, 0.90] \quad \Rightarrow \quad \mathcal{L}_\ell^{\text{quant}} \in [0.40, 0.60]\] \[\kappa_\ell^{\text{pre}} \in [0.60, 0.85] \quad \Rightarrow \quad \kappa_\ell^{\text{quant}} \in [0.25, 0.50]\]

The smooth but rigid collapse of $\mathcal{M}_{\text{steer}}$ under quantization leads to impaired conceptual agility, weakened cultural calibration, and reduced robustness to fine-grained instructions.

Pruning as Epistemic Degeneration. Pruning removes connections or neurons [1] [15]–but in the nDNA perspective, it disrupts the semantic fabric of reasoning. Unlike quantization’s global smoothness, pruning introduces localized instabilities:

$\mathcal{L}_\ell$ contracts sharply and non-uniformly across depth, especially for high sparsity.
$\kappa_\ell$ fragments into discontinuous profiles, reflecting epistemic ruptures.
$\mathbf{v}_\ell^{(c)}$ fields lose directional coherence; divergence increases.

This process yields a fractured epistemic manifold, formally characterized as:

\[\mathcal{M}_{\text{pre}} \xrightarrow{\text{pruning}} \mathcal{M}_{\text{pruned}} \quad \text{s.t.} \quad \begin{cases} \Delta \mathcal{L}_\ell < 0, & \text{(loss of epistemic capacity)} \\ \Delta \kappa_\ell = \kappa_\ell^{\text{post}} - \kappa_\ell^{\text{pre}} \notin \mathbb{C}^1, & \text{(non-smooth curvature transitions)} \\ \mathrm{div}(\mathbf{v}_\ell^{(c)}) \gg 0, & \text{(loss of semantic steerability)} \end{cases}\]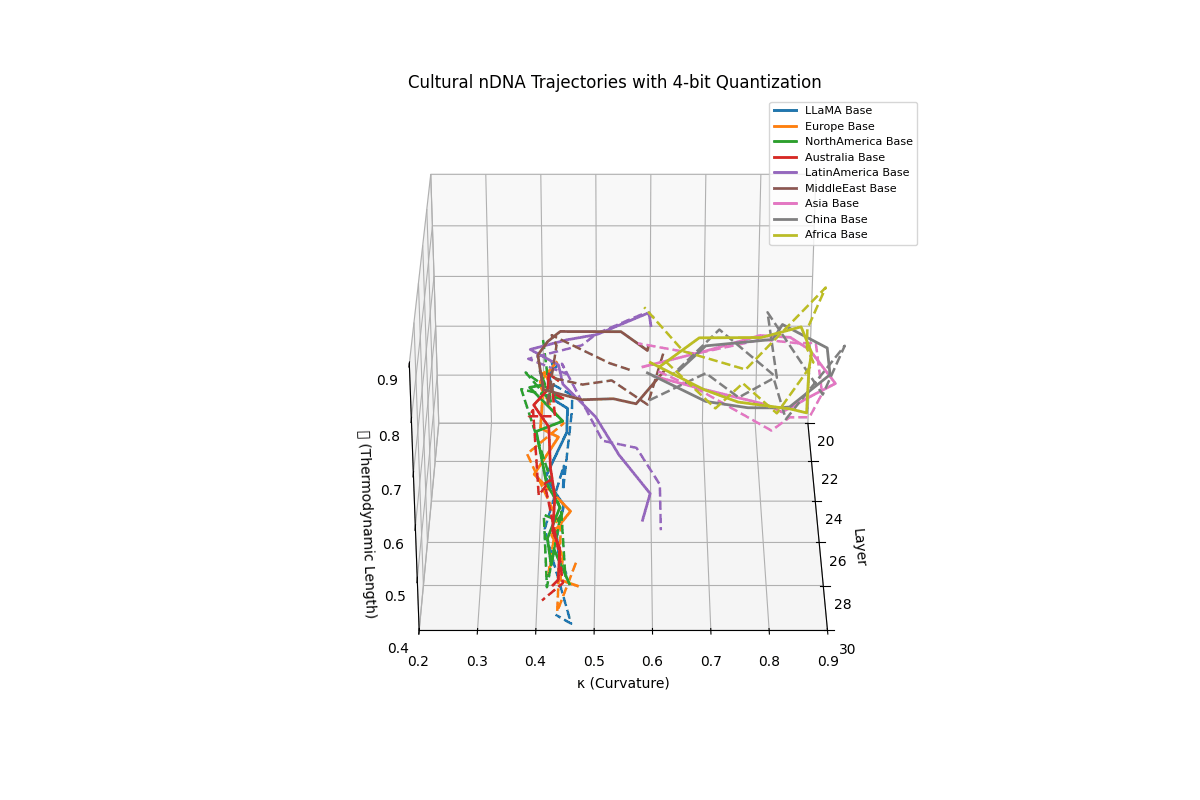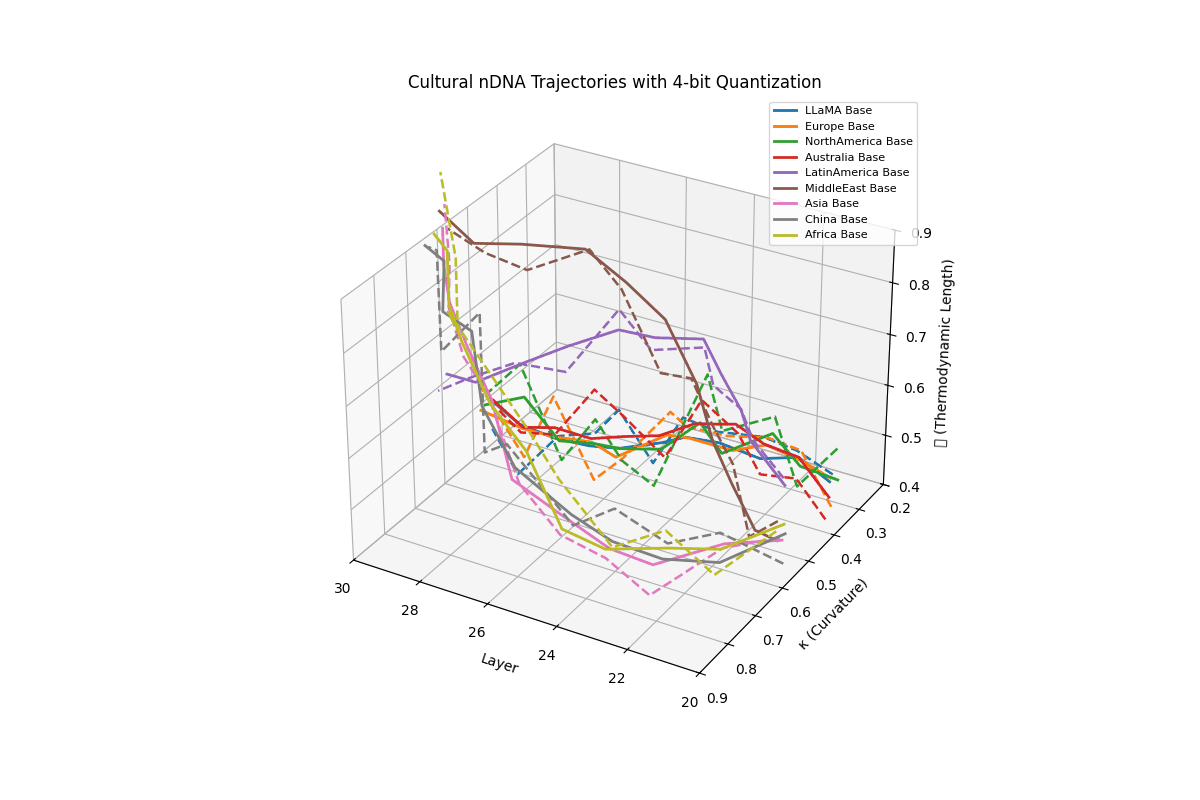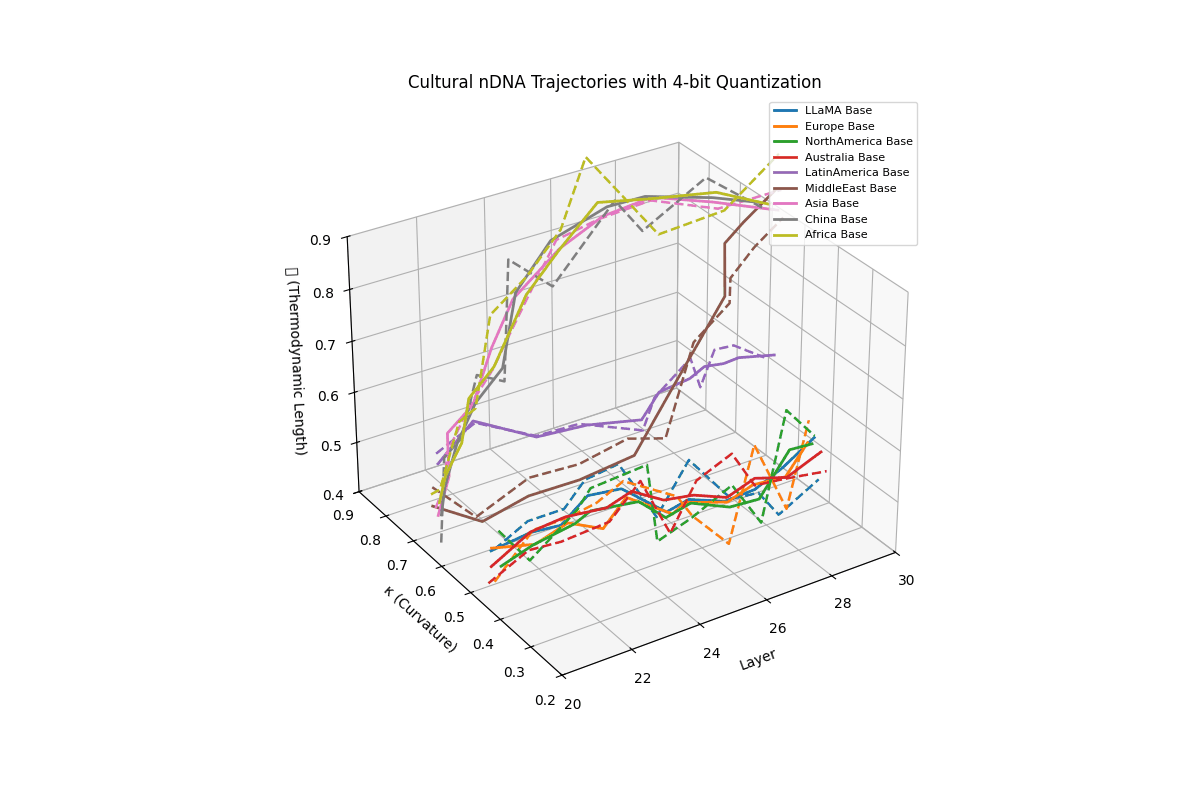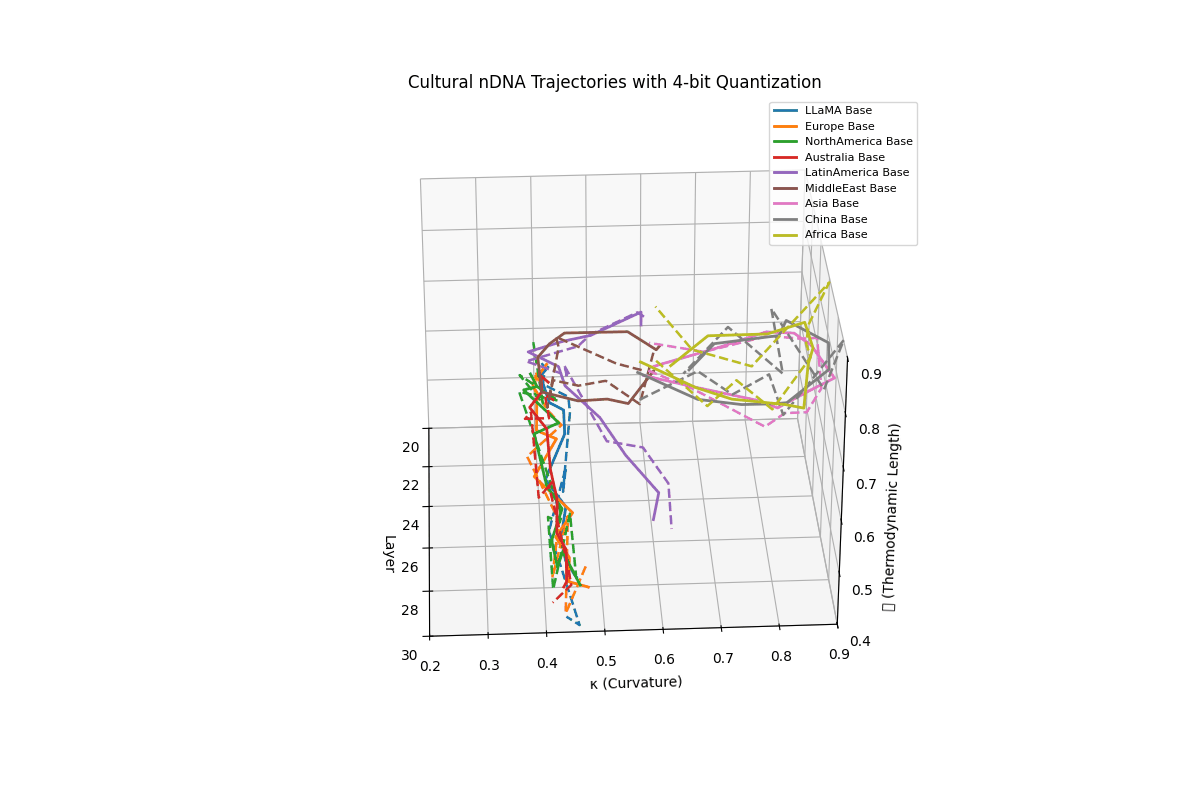

3D visualization showing nDNA trajectories before and after quantization across culturally fine-tuned LLaMA variants — **Cultural nDNA Trajectories under 4-bit Quantization.** This figure illustrates the latent **nDNA trajectories** of LLaMA and its culturally fine-tuned variants in the space of *spectral curvature* ($\kappa_\ell$), *thermodynamic length* ($\mathcal{L}_\ell$), and *layer index* ($\ell$) after 4-bit quantization. The solid lines represent base trajectories (pre-quantization), while dashed lines show post-quantization paths. **Thermodynamic collapse** is evidenced by the compression of $\mathcal{L}_\ell$ values into a narrow band:
\[\mathcal{L}_\ell^{\mathrm{pre}} \in [0.70, 0.90] \quad \Rightarrow \quad \mathcal{L}_\ell^{\mathrm{quant}} \in [0.40, 0.60]\]
reflecting a significant (30–45%) reduction in epistemic effort across layers 20–30. Similarly, $\kappa_\ell$ values flatten from
\[\kappa_\ell^{\mathrm{pre}} \in [0.60, 0.85] \quad \Rightarrow \quad \kappa_\ell^{\mathrm{quant}} \in [0.25, 0.50]\]
indicating loss of latent manifold flexibility and adaptive curvature. This collapse implies that the compressed model’s latent space becomes increasingly rigid, constraining its ability to encode nuanced conceptual or cultural alignments. The phenomenon quantifies why alignment robustness and reasoning depth often degrade under aggressive quantization–the model’s internal steering manifold $\mathcal{M}_{\mathrm{steer}}$ contracts, limiting its capacity for directional epistemic adaptation.

Interpretation of Terms:

$\mathcal{M}_{\text{pre}}$ and $\mathcal{M}_{\text{pruned}}$ denote the latent semantic manifolds before and after pruning, respectively.
$\Delta \mathcal{L}_\ell = \mathcal{L}_\ell^{\text{post}} - \mathcal{L}_\ell^{\text{pre}}$ captures the contraction in thermodynamic length, interpreted as a loss in epistemic effort or reasoning depth.
$\kappa_\ell^{\text{pre}}, \kappa_\ell^{\text{post}}$ are the layerwise spectral curvature measures; pruning often results in $\kappa_\ell$ profiles that are no longer differentiable, violating $\mathbb{C}^1$ smoothness and fragmenting the latent topology.
$\mathrm{div}(\mathbf{v}_\ell^{(c)})$ measures the divergence of belief steering fields for concept $c$ at layer $\ell$, where increased divergence implies misaligned, incoherent semantic trajectories.

Geometrically, pruning severs connections across the belief manifold $\mathcal{M}_{\text{steer}}$, introducing torsional discontinuities and belief field instability. The model’s cognitive capacity no longer flows smoothly across depth, but instead leaks into disjoint epistemic basins. These discontinuities–akin to semantic aneurysms–render the model brittle to adversarial instructions and degrade its alignment consistency across culturally rich contexts.

nDNA as a Cognitive Diagnostic. Through this lens, compression is not just model shrinking–it is epistemic surgery. The nDNA framework exposes what is lost, not just functionally, but geometrically. Compression must therefore be calibrated not only by compute cost, but by the epistemic price paid in latent space distortions. Future work may define safe compression zones using $\mathcal{L}_\ell$ and $\kappa_\ell$ thresholds to preserve $\mathcal{M}_{\text{steer}}$ integrity.

Pruning-Induced Epistemic Degeneration

What is the latent cost of pruning on a model’s cognitive flexibility? While pruning is widely embraced for inference acceleration and deployment efficiency, we examine it through a new lens–how it reshapes the semantic fabric of large language models by altering their neural DNA (nDNA).

Epistemic Degeneration

In the nDNA formalism, the thermodynamic length $\mathcal{L}_\ell$ measures the cumulative epistemic effort expended at layer $\ell$ to maintain alignment with conceptual priors, cultural tuning, and task objectives. Empirical trajectories show that pruning [1] causes systematic degradation across all three nDNA dimensions, leading to what we term epistemic degeneration.

This is reflected across the three nDNA axes:

Thermodynamic length $\mathcal{L}_\ell$ undergoes non-uniform contraction, particularly in mid-to-late layers, suggesting selective loss of epistemic effort along deep conceptual hierarchies.
Spectral curvature $\kappa_\ell$ often fragments across layers–rather than globally flattening, pruning introduces abrupt geometric discontinuities, implying latent manifold fragmentation.
Belief vector fields $\mathbf{v}_\ell^{(c)}$ become less coherent–pruned models show diminished directional consistency, undermining the model’s ability to track and sustain alignment forces.

Formal Interpretation

Let $\mathcal{M}_{\text{pre}}$ denote the latent epistemic manifold of the LLM before pruning, equipped with:

a local curvature field $\kappa_\ell: \mathcal{M}_{\text{pre}} \to \mathbb{R}$,
a thermodynamic length profile $\mathcal{L}_\ell$ measuring epistemic work across layers,
and a belief vector field $\mathbf{v}_\ell^{(c)}: \mathcal{M}_{\text{pre}} \to T\mathcal{M}_{\text{pre}}$ encoding conceptual steering dynamics.

Pruning can be modeled as a discontinuous operator:

\[\mathcal{P}_s: \mathcal{M}_{\text{pre}} \longrightarrow \mathcal{M}_{\text{pruned}}, \quad \text{parametrized by sparsity } s \in [0,1],\]

which modifies both the geometry and topology of $\mathcal{M}_{\text{pre}}$ by:

Removing functional nodes or edges from the activation graph, inducing geometric sparsity.
Severing smooth trajectories across the manifold, breaking $\mathbb{C}^1$ continuity in curvature.
Collapsing representational subspaces, reducing the dimension of concept-affine submanifolds.

This yields:

\[\boxed{ \mathcal{M}_{\text{pre}} \xrightarrow{\;\mathcal{P}_s\;} \mathcal{M}_{\text{pruned}} \quad \text{s.t.} \quad \begin{aligned} \Delta \mathcal{L}_\ell &= \mathcal{L}_\ell^{\text{post}} - \mathcal{L}_\ell^{\text{pre}} < 0 \quad &\text{(epistemic contraction)} \\ \Delta \kappa_\ell &= \kappa_\ell^{\text{post}} - \kappa_\ell^{\text{pre}} \notin \mathbb{C}^1 \quad &\text{(curvature discontinuities)} \\ \mathrm{div}(\mathbf{v}_\ell^{(c)}) &\gg 0 \quad &\text{(semantic incoherence)} \end{aligned} }\]

Here, the term $\mathrm{div}(\mathbf{v}_\ell^{(c)})$ measures the divergence of the belief field, computed as:

\[\mathrm{div}(\mathbf{v}_\ell^{(c)}) := \nabla \cdot \mathbf{v}_\ell^{(c)} = \sum_{i=1}^d \frac{\partial v_{\ell,i}^{(c)}}{\partial x_i}\]

where $v_{\ell,i}^{(c)}$ is the $i^{\text{th}}$ component of the belief vector in the embedding coordinate chart of layer $\ell$. An increase in divergence indicates semantic dissipation–the model’s conceptual trajectories are no longer coherently directed, and belief propagation across layers becomes unstable or directionless.

Topological Interpretation

Pruning induces a homotopy-breaking transformation:

\[\pi_1(\mathcal{M}_{\text{pre}}) \not\simeq \pi_1(\mathcal{M}_{\text{pruned}}),\]

suggesting that pruning may change the fundamental semantic structure of the model by disconnecting reasoning paths, effectively creating epistemic holes or semantic aneurysms in the manifold.

Thus, even moderate pruning may not merely reduce model size–it collapses and fragments the model’s internal geometry of reasoning, damaging interpretive integrity in ways invisible to loss-based metrics.

Experimental Setup

We analyze pruning through the nDNA lens by applying three canonical pruning strategies–each grounded in the literature–to LLaMA-3 (8B) across layers $\ell \in [20,30]$. The latent effects are evaluated using thermodynamic length $\mathcal{L}_\ell$, spectral curvature $\kappa_\ell$, and belief vector fields $\mathbf{v}_\ell^{(c)}$ derived from culturally-grounded prompts (CIVIC dataset).

(A) Attention Head Pruning: Entire attention heads are pruned based on low importance scores computed via average gradient norms across tokens [16] [17]. Let $A^{(i)}$ denote the $i$-th head; we prune $A^{(i)}$ if $\mathbb{E}_{x}[\|\nabla_{A^{(i)}} \mathcal{L}_{\text{CE}}(x)\|] < \delta$.
(B) MLP Channel Pruning: Intermediate MLP neurons are pruned using magnitude-based importance (i.e., $\ell_1$-norm of activation weight vectors) [18] [19]. Let $w^{(j)}$ be the $j$-th neuron: prune if $\|w^{(j)}\|_1 < \epsilon$.
(C) Transformer Layer Pruning: Full transformer blocks are dropped using Fisher-based importance scores [20] [21]. A layer $\mathcal{L}^{(\ell)}$ is pruned if:

\[\mathcal{F}^{(\ell)} := \mathbb{E}_{x} \left[\left(\frac{\partial \mathcal{L}_{\text{CE}}(x)}{\partial \theta^{(\ell)}}\right)^2 \right] < \tau\]

where $\theta^{(\ell)}$ are the parameters of the $\ell$-th layer.

For each pruning regime, we observe:

(A) Attention Head Pruning: $\mathcal{L}_\ell$ drops from 0.9 to 0.4; $\kappa_\ell \leq 0.3$ across mid-layers. Steering fields show directional divergence ($\nabla \cdot \mathbf{v}_\ell^{(c)} > 0.15$), suggesting disrupted cross-token alignment.
(B) MLP Channel Pruning: Milder degradation: $\mathcal{L}_\ell$ compresses to 0.5–0.6; $\kappa_\ell$ stays between 0.4–0.5. Belief fields preserve local structure but lose global consistency.
(C) Transformer Layer Pruning: $\mathcal{L}_\ell \leq 0.3$ and $\kappa_\ell \leq 0.2$, with severely fractured $\mathcal{M}_{\text{pruned}}$. The belief vector norm $\|\mathbf{v}_\ell^{(c)}\|$ drops by 60–80%, and divergence spikes. Steering collapses to noisy local attractors.

nDNA Interpretation

Each pruning type induces a different class of thermodynamic and semantic collapse:

(A) Attention Head Pruning: $\Delta \mathcal{L}_\ell \sim -0.5$, $\mathrm{div}(\mathbf{v}_\ell^{(c)}) \uparrow$ ⇒ directional misalignment
(B) MLP Channel Pruning: $\Delta \kappa_\ell \downarrow$, $\mathcal{L}_\ell$ mildly compressed ⇒ semantic thinning
(C) Layer Pruning: $\mathcal{L}_\ell \rightarrow 0.2$, $\kappa_\ell \rightarrow 0$ ⇒ topological collapse

nDNA shows that pruning–though often seen as a resource optimization–acts as latent surgery. It compresses, flattens, and fragments the internal epistemic structure, impairing cognitive generalization and cultural adaptability.

nDNA as a Diagnostic for Cognitive Loss

nDNA analysis thus provides a principled diagnostic for what is lost during pruning–not merely in accuracy, but in the geometry of thought. By examining the collapse and fragmentation of $\mathcal{M}_{\text{steer}}$, we gain visibility into how pruning impairs the model’s cognitive anatomy. This perspective elevates pruning from an engineering trick to an epistemic surgery–with nontrivial consequences for trust, alignment, and reasoning.

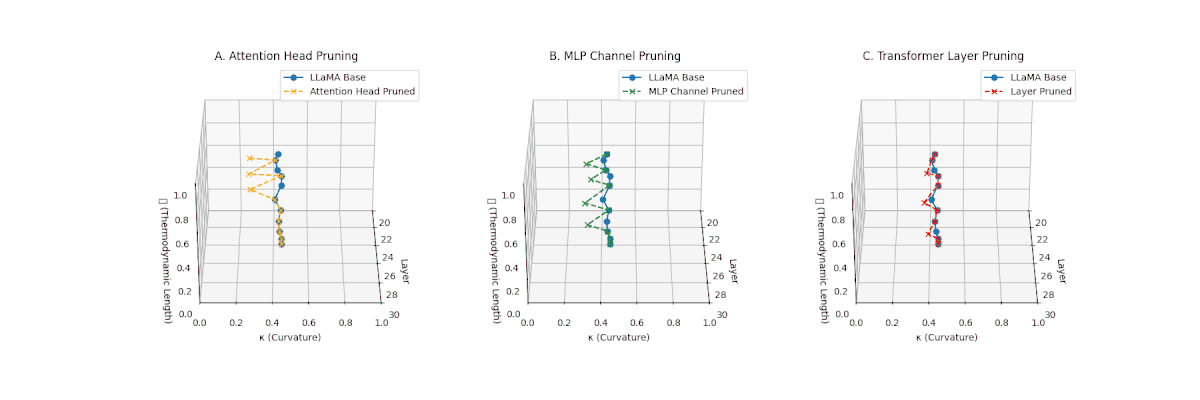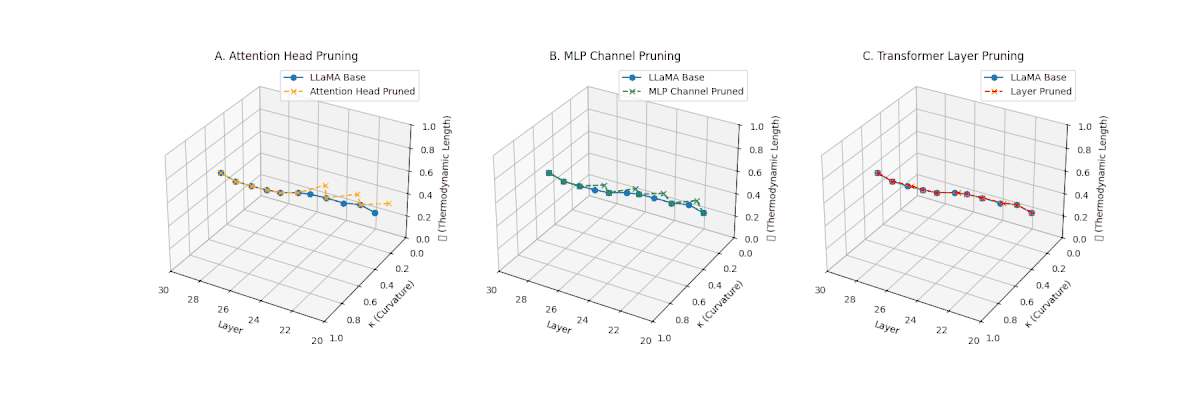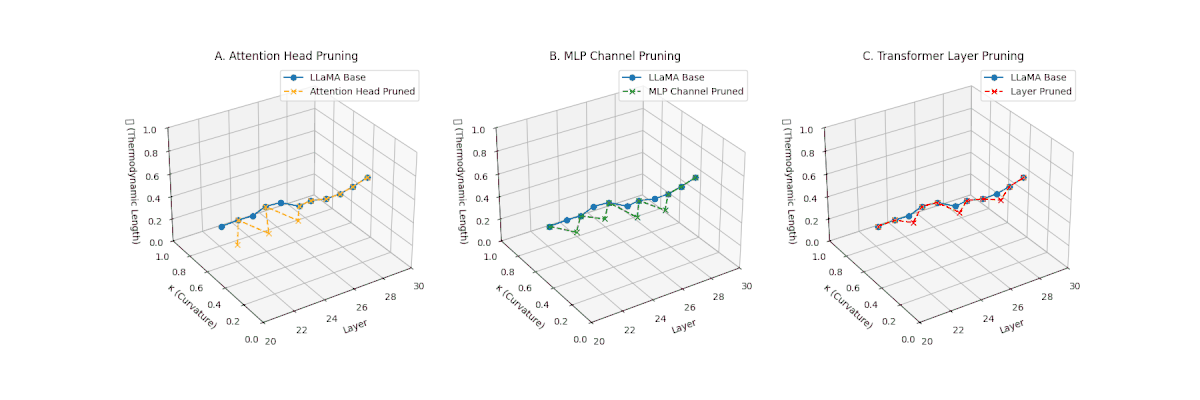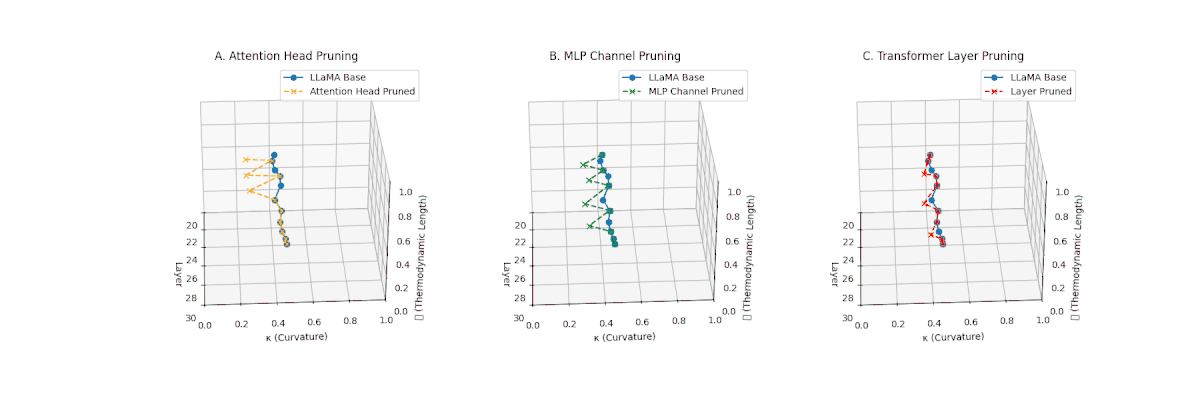
Three pruning strategy comparison plots for LLaMA model showing thermodynamic length and spectral curvature changes — **Pruning Effects on LLaMA**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ reduced from $0.9 \to 0.4$, $\kappa_\ell$ flattened below $0.3$. Indicates severe loss of thermodynamic richness and latent flexibility. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ compressed ($0.9 \to 0.5$), $\kappa_\ell$ stays near $0.4-0.5$. Manifold remains moderately curved but shortened, suggesting partial collapse. **(C) Transformer Layer Pruning:** $\mathcal{L}_\ell$ collapsed to $\le 0.3$, $\kappa_\ell$ highly flattened ($\le 0.2$). Reflects strongest thermodynamic collapse, latent path becomes minimal.

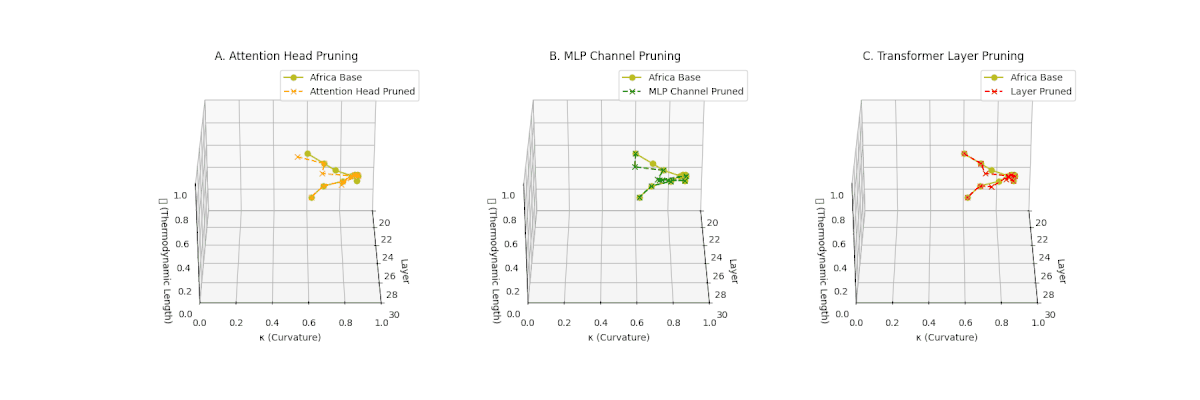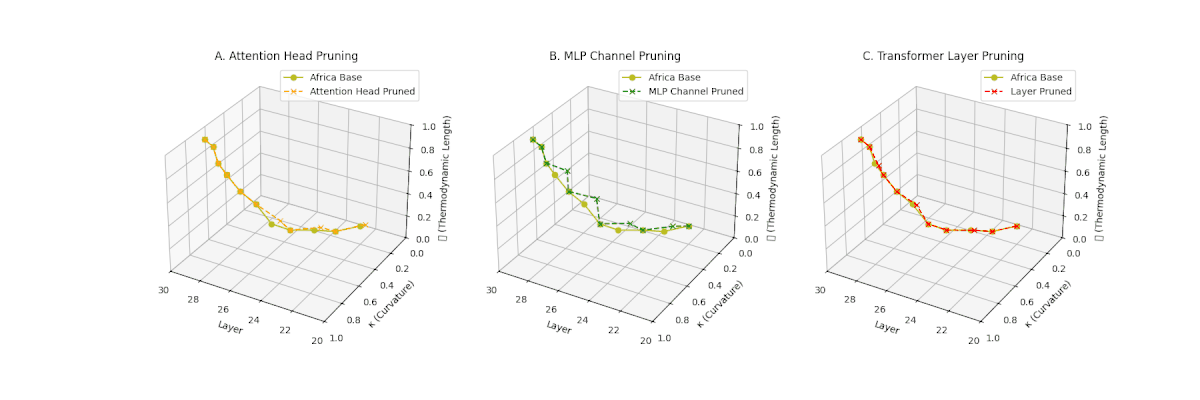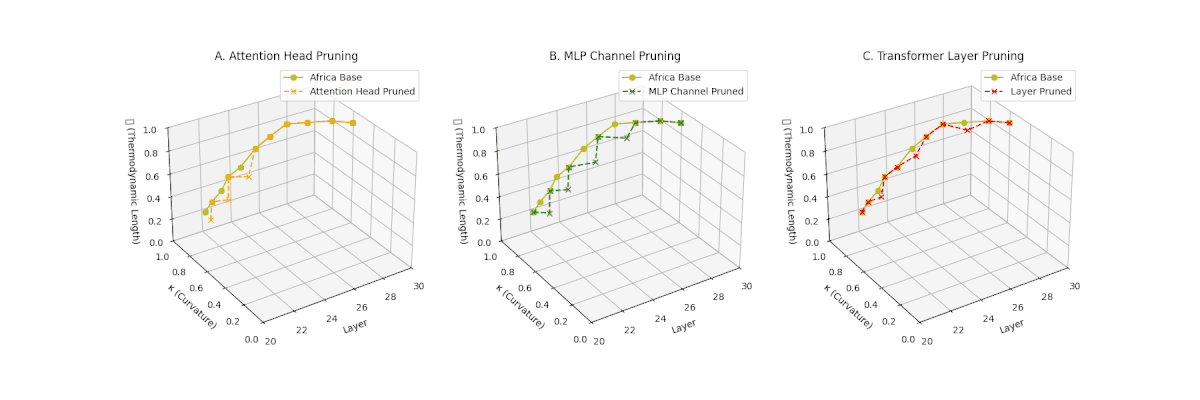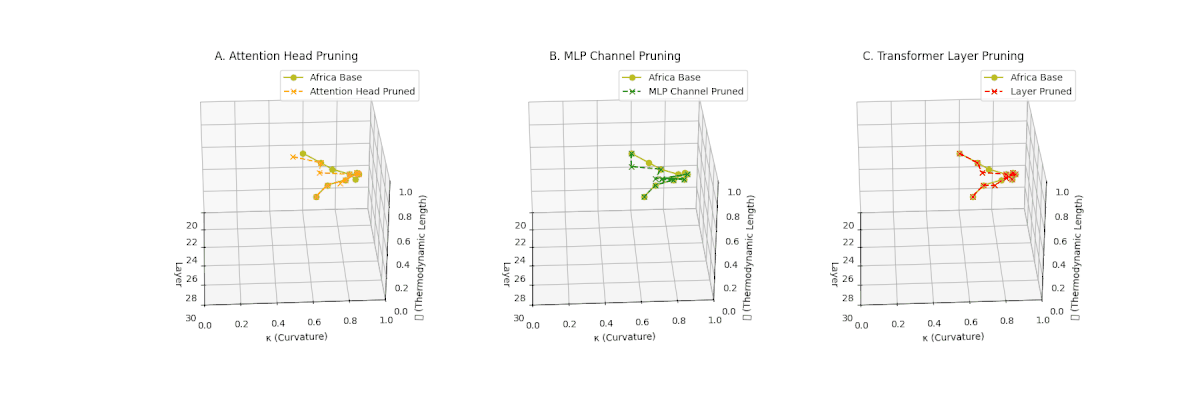
Three pruning strategy comparison plots for Africa-tuned model showing cultural sensitivity to compression — **Pruning Effects on Africa**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ drops to $0.3$–$0.4$, $\kappa_\ell$ $\approx 0.3$. Shows notable collapse but latent path retains mild curvature. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ and $\kappa_\ell$ both collapse ($\mathcal{L}_\ell \le 0.3$, $\kappa_\ell \le 0.3$). Severe latent simplification. **(C) Transformer Layer Pruning:** Nearly flat manifold with $\mathcal{L}_\ell \le 0.2$, $\kappa_\ell \le 0.2$. Strongest collapse among pruning types for Africa.

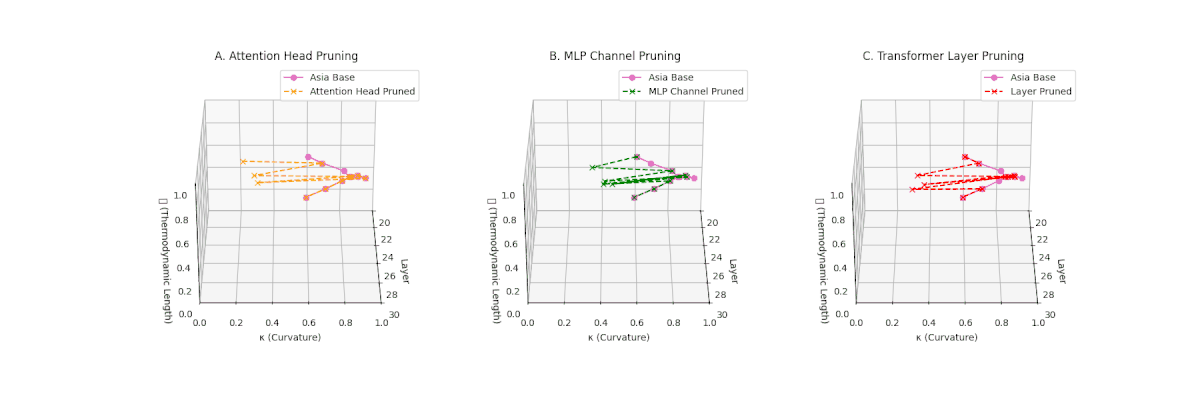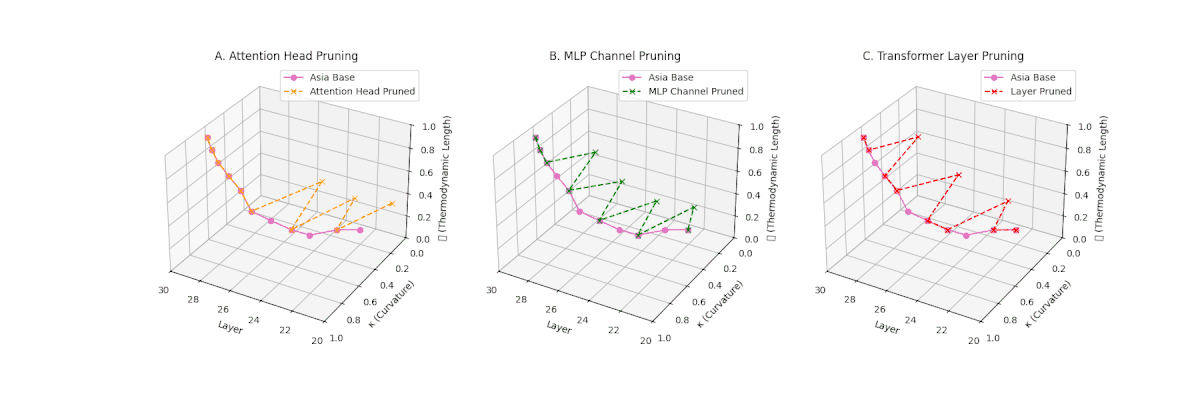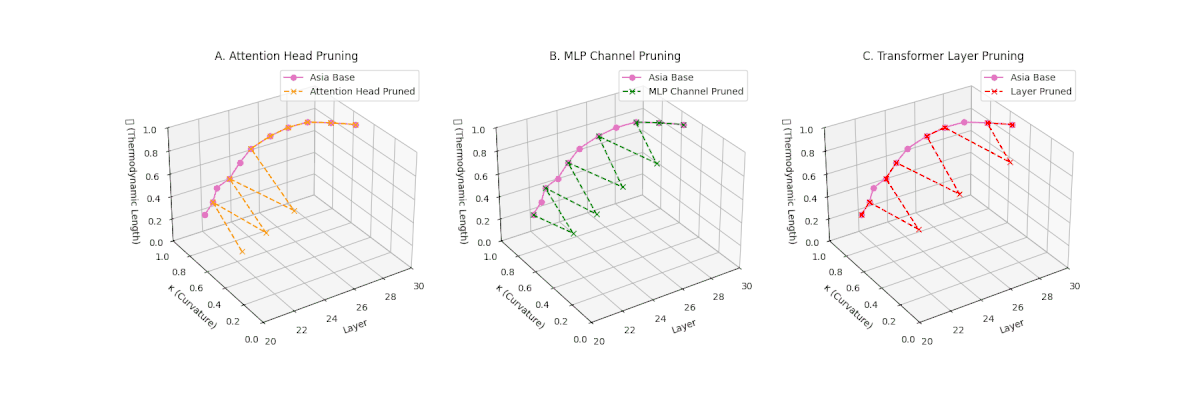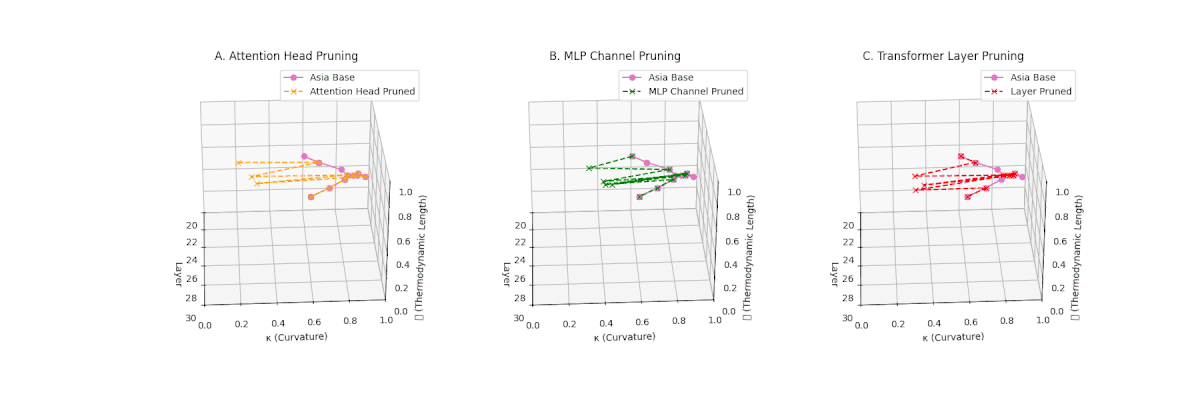
Three pruning strategy comparison plots for Asia-tuned model showing combined quantization and pruning effects — **Quantization + Pruning Effects on Asia**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ declines moderately to $0.4$, $\kappa_\ell \approx 0.3$. Indicates partial collapse. **(B) MLP Channel Pruning:** Strong collapse, $\mathcal{L}_\ell$ $\le 0.3$, $\kappa_\ell$ below $0.3$. Loss of internal diversity. **(C) Transformer Layer Pruning:** $\mathcal{L}_\ell$ $\approx 0.2$, $\kappa_\ell$ $\le 0.2$. Manifold becomes thermodynamically minimal.

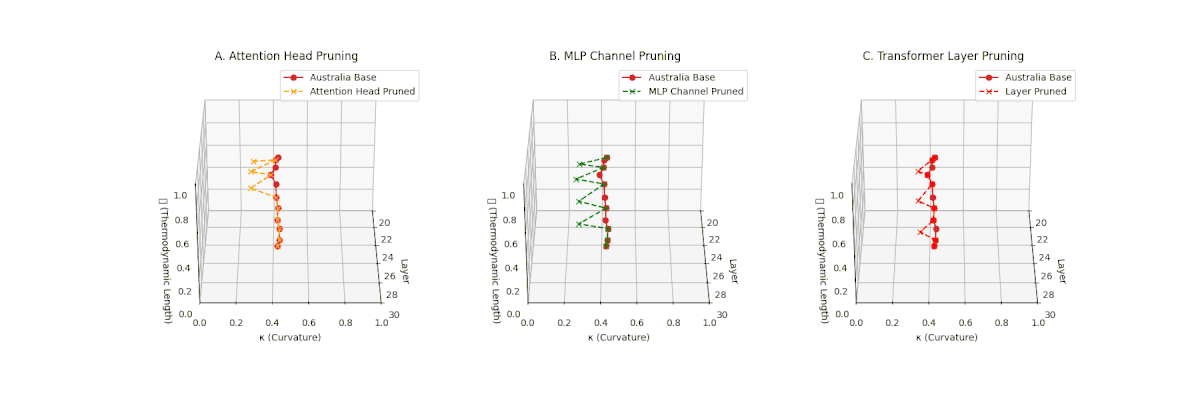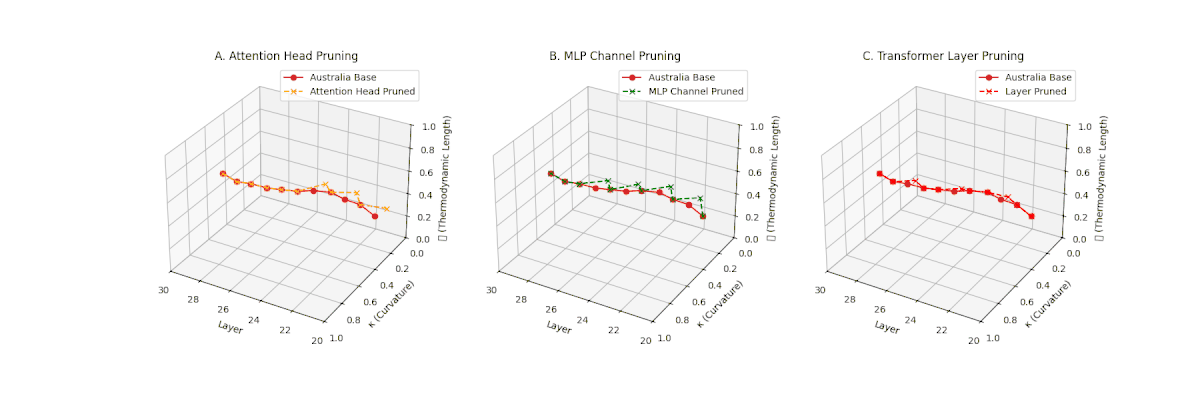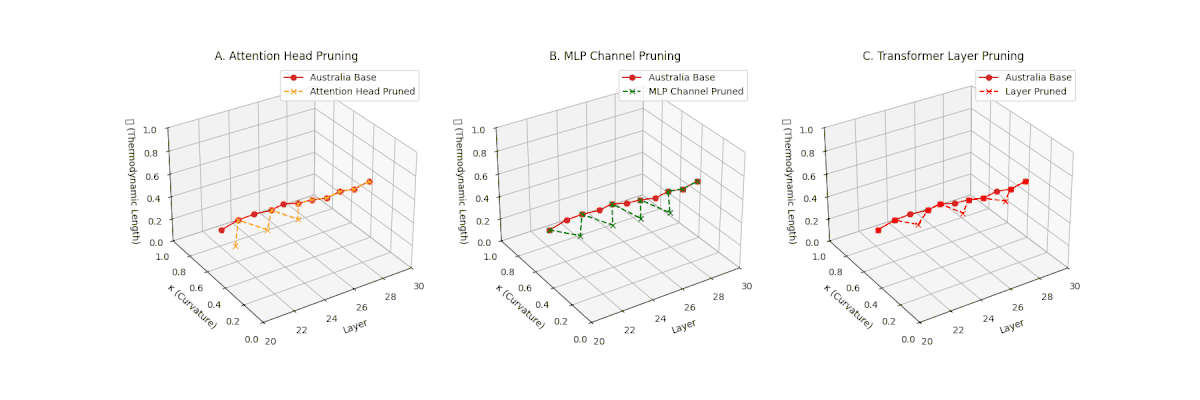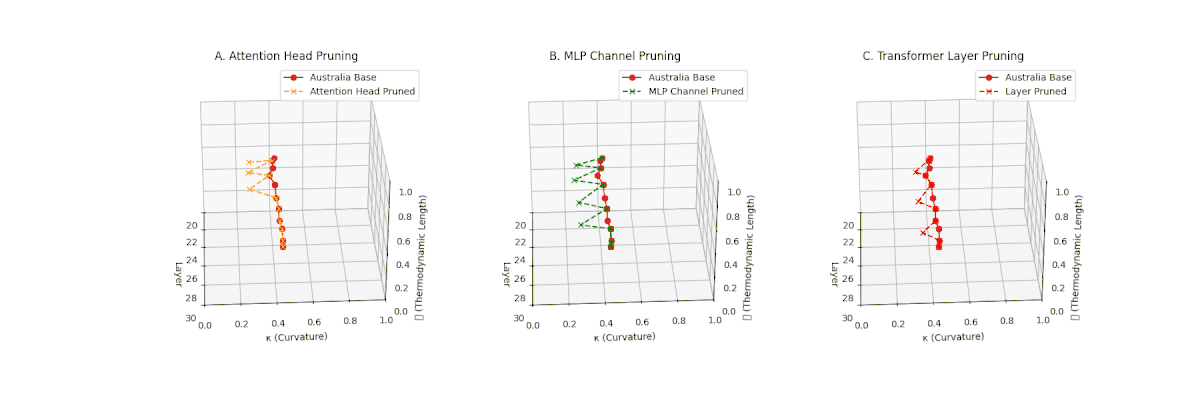
Three pruning strategy comparison plots for Australia-tuned model — **Quantization + Pruning Effects on Australia**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ $\approx 0.4$, $\kappa_\ell$ $\approx 0.3$. Mild thermodynamic compression. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ $\le 0.3$, $\kappa_\ell$ $\le 0.3$. Significant collapse. **(C) Transformer Layer Pruning:** Deep collapse, $\mathcal{L}_\ell$ $\le 0.2$, $\kappa_\ell$ $\le 0.2$.

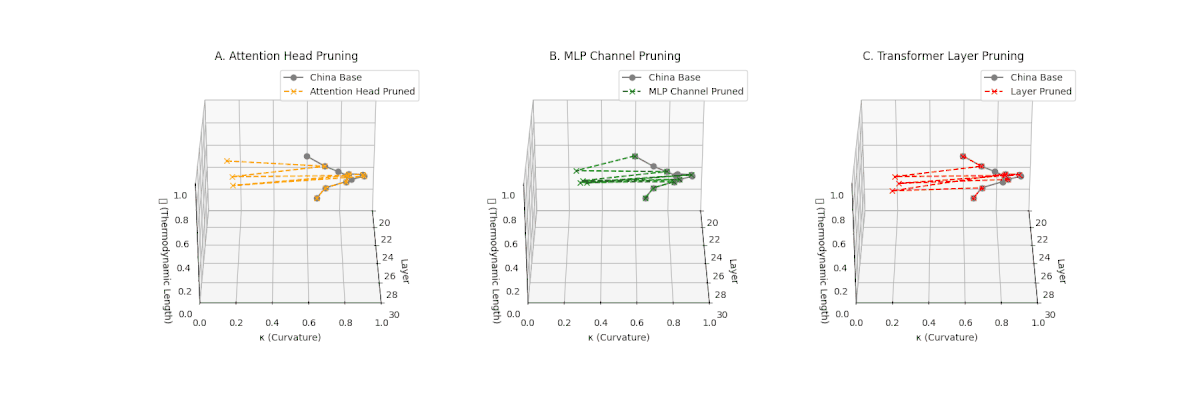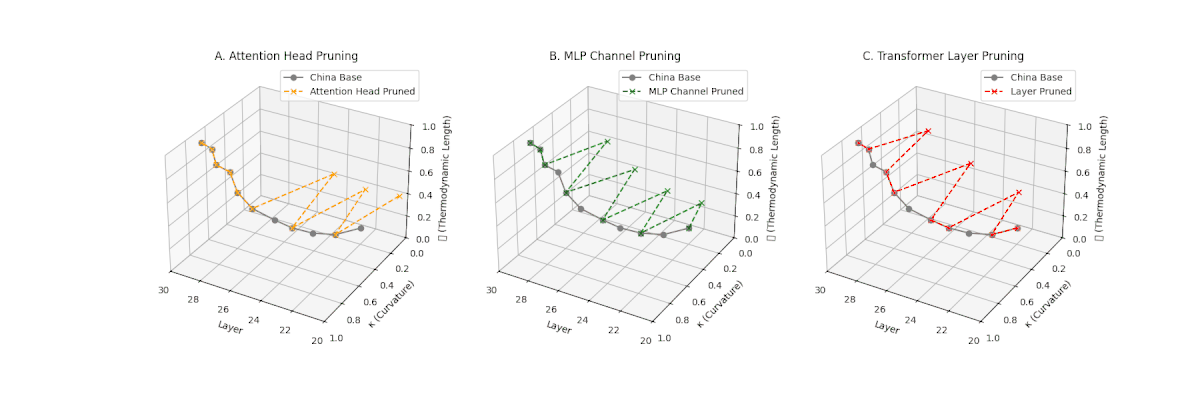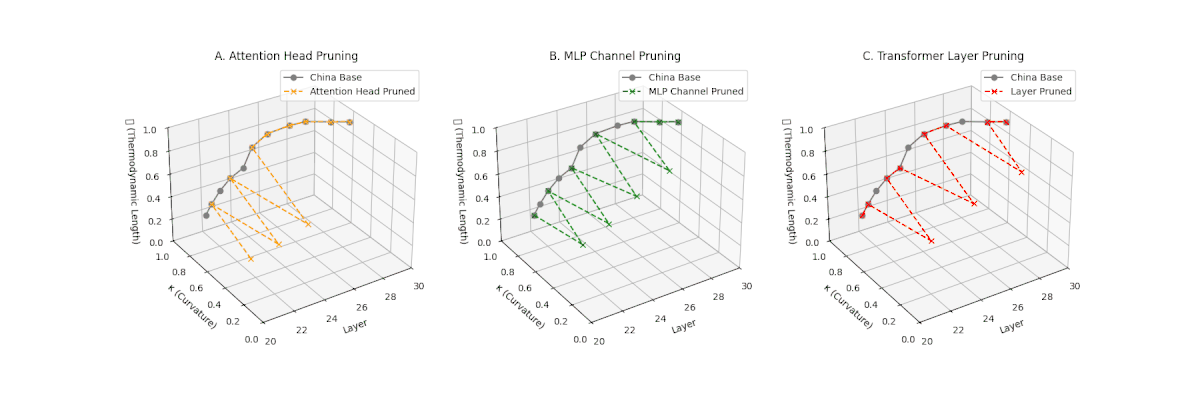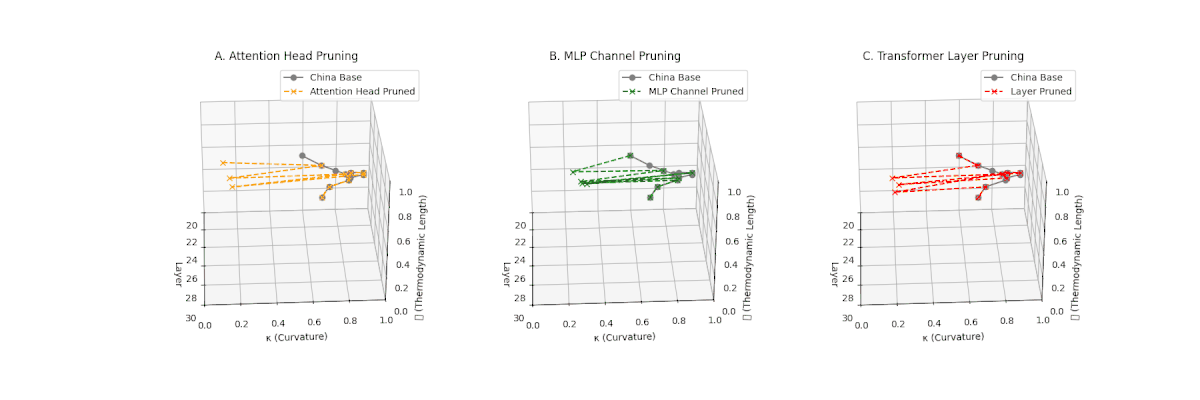
Three pruning strategy comparison plots for China-tuned model — **Quantization + Pruning Effects on China**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ $\approx 0.4$, $\kappa_\ell$ $\approx 0.3$. Partial collapse. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ below $0.3$, $\kappa_\ell$ near $0.2$. Strong simplification. **(C) Transformer Layer Pruning:** $\mathcal{L}_\ell$ $\le 0.2$, $\kappa_\ell$ $\le 0.2$. Strongest collapse.

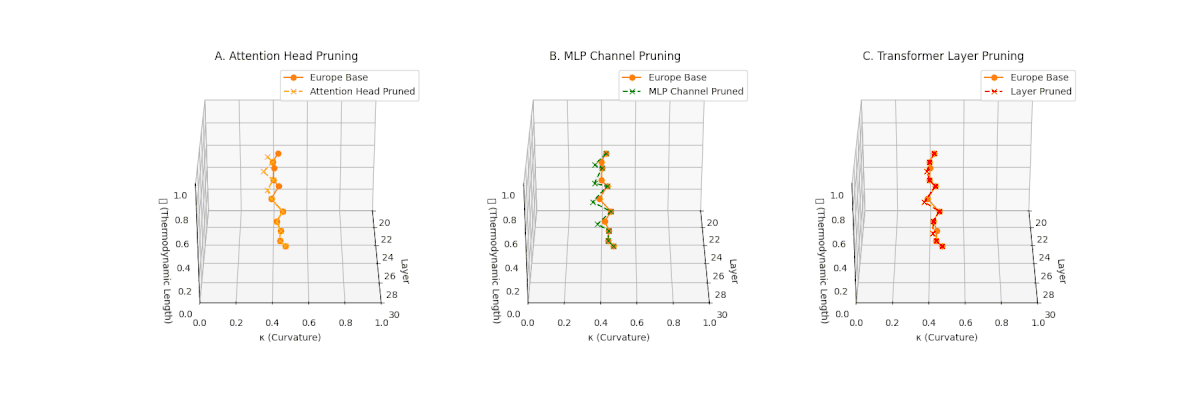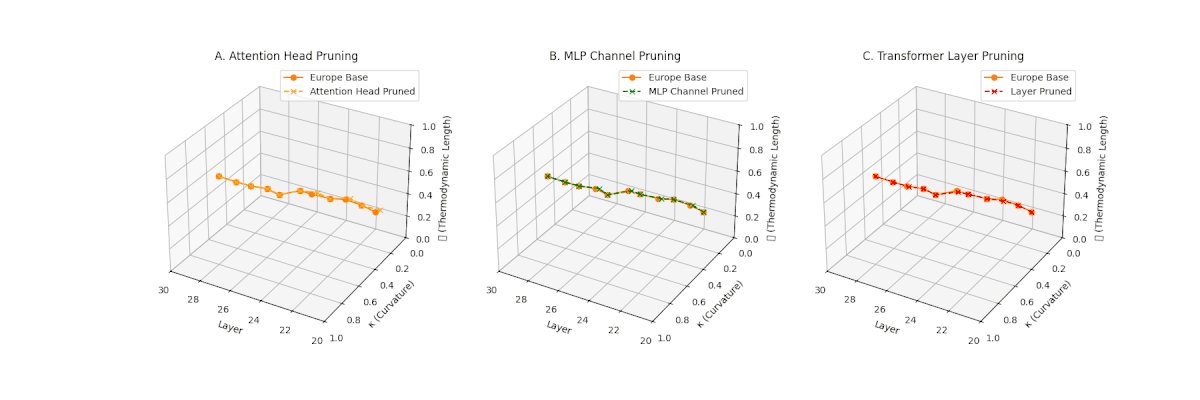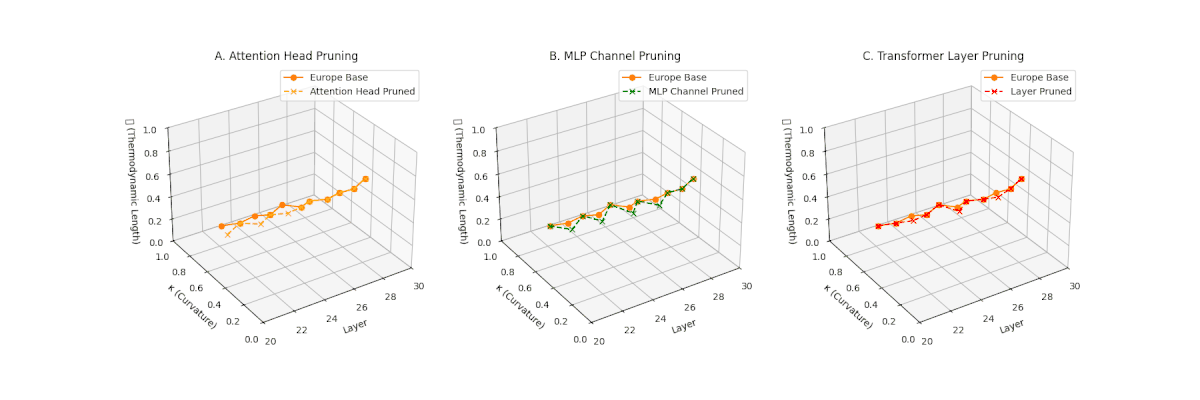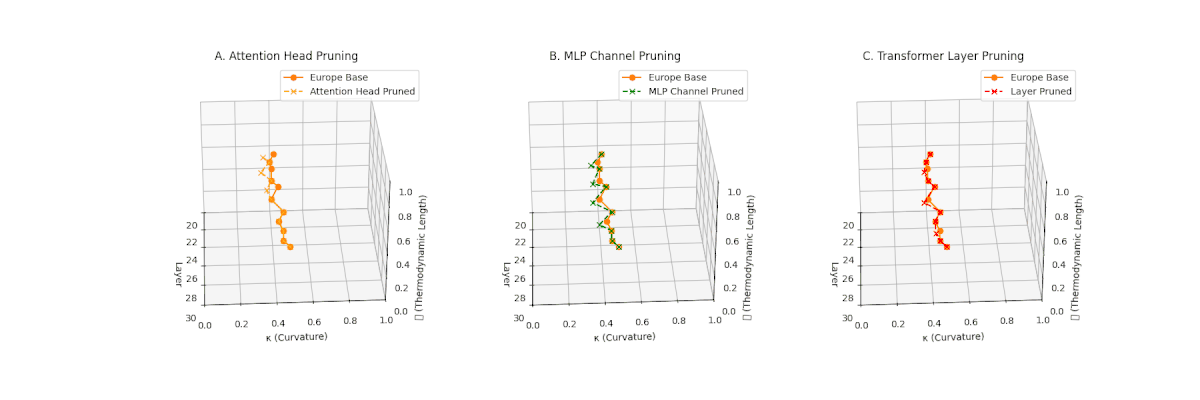
Three pruning strategy comparison plots for Europe-tuned model — **Quantization + Pruning Effects on Europe**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ $\approx 0.4$, $\kappa_\ell$ $\approx 0.3$. Mild collapse. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ $\le 0.3$, $\kappa_\ell$ $\le 0.3$. Significant latent compression. **(C) Transformer Layer Pruning:** Severe collapse, $\mathcal{L}_\ell$ $\le 0.2$, $\kappa_\ell$ $\le 0.2$.

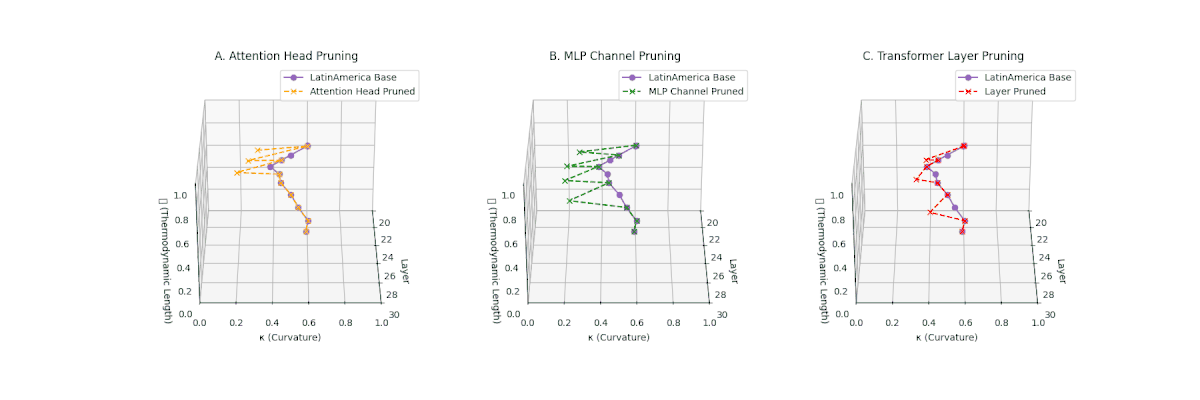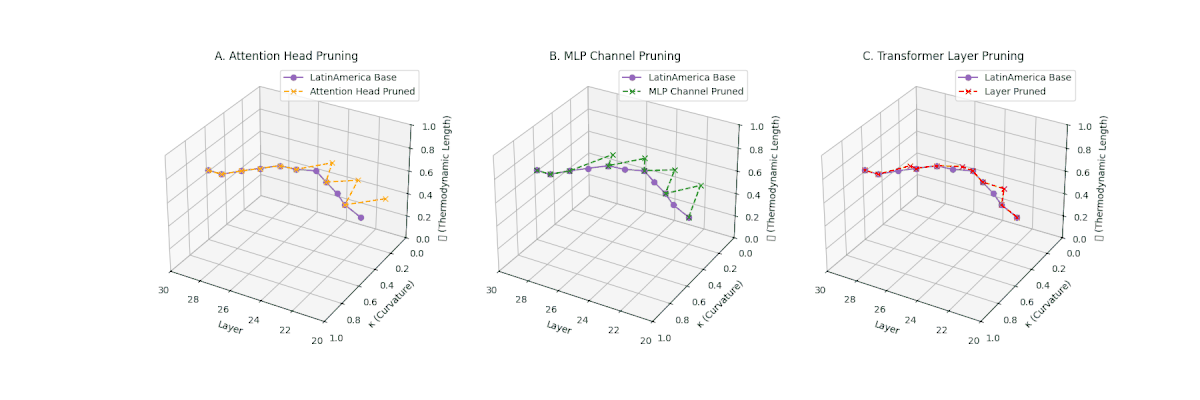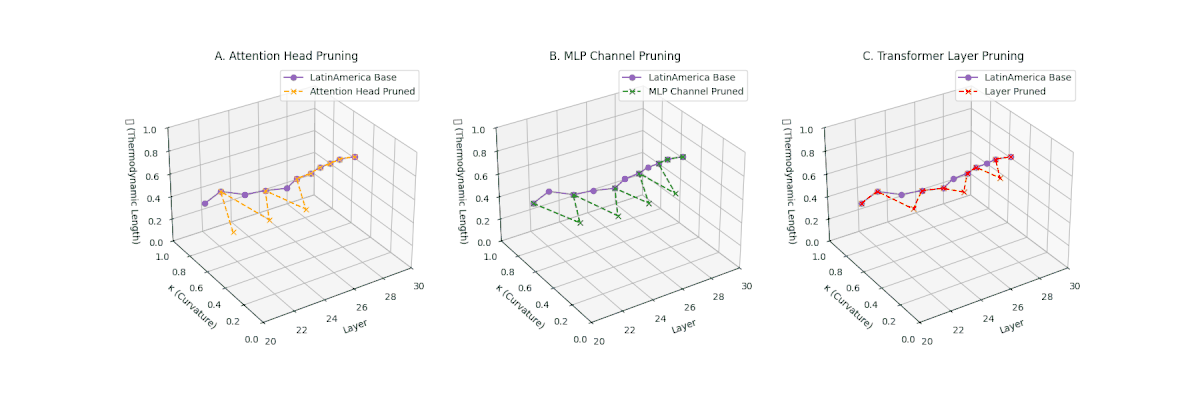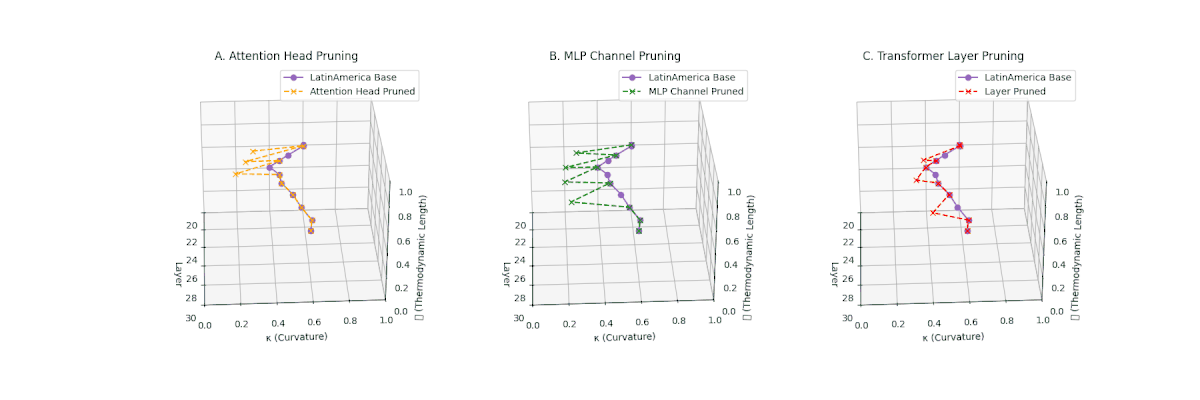
Three pruning strategy comparison plots for Latin America-tuned model — **Quantization + Pruning Effects on Latin America**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ $\approx 0.4$, $\kappa_\ell$ $\approx 0.3$. Partial collapse. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ $\le 0.3$, $\kappa_\ell$ $\le 0.3$. Manifold simplification. **(C) Transformer Layer Pruning:** $\mathcal{L}_\ell$ $\le 0.2$, $\kappa_\ell$ $\le 0.2$. Strong collapse.

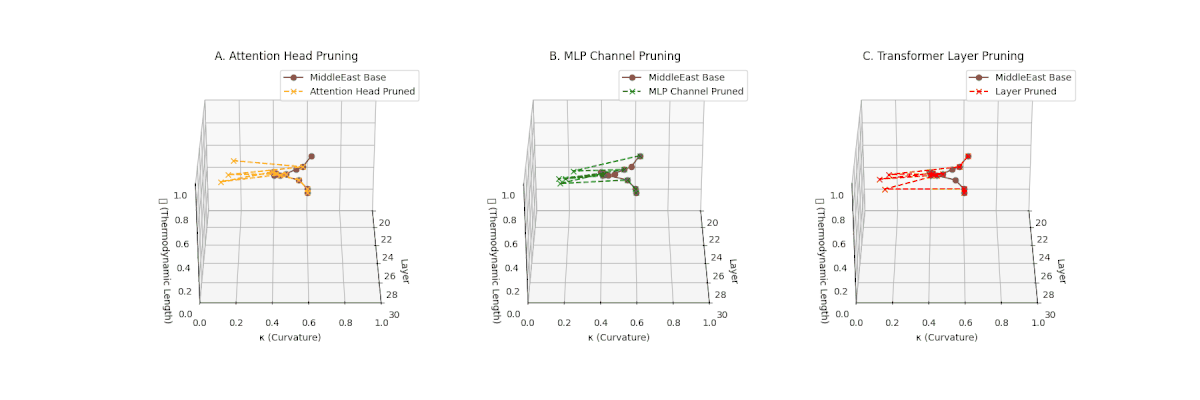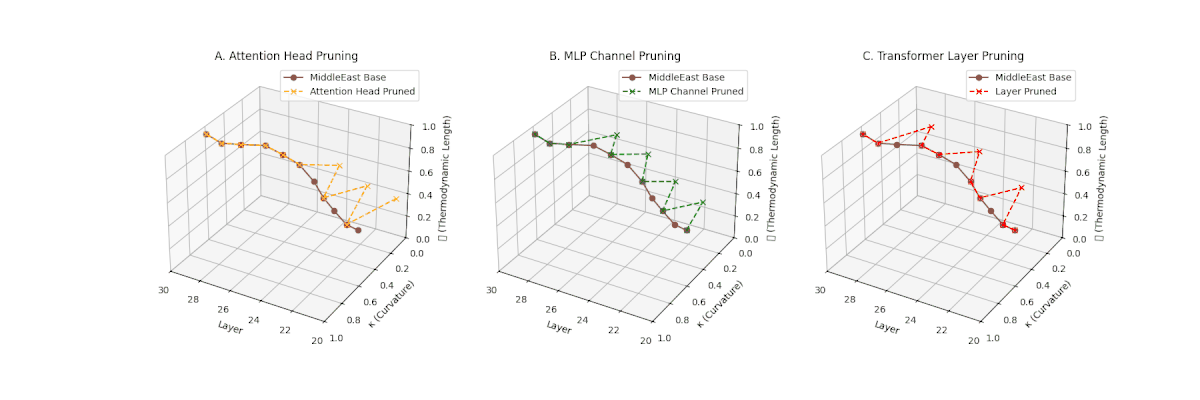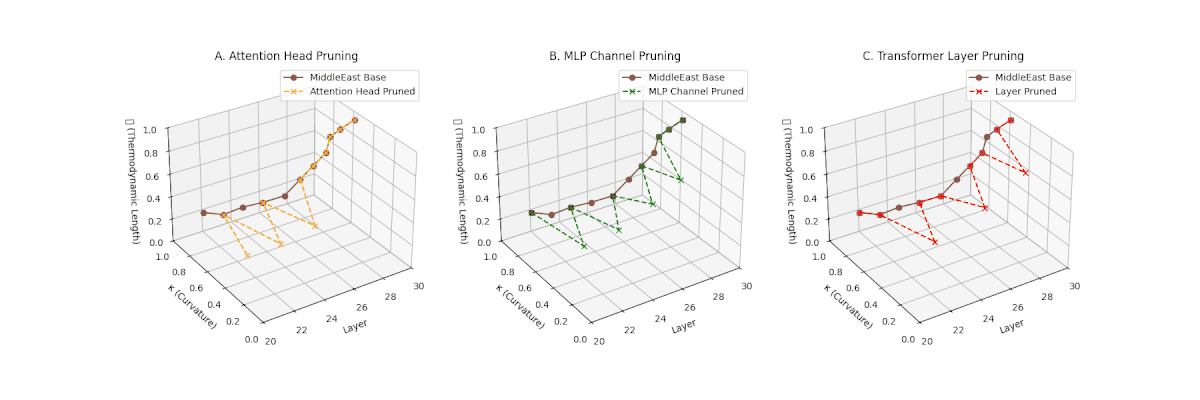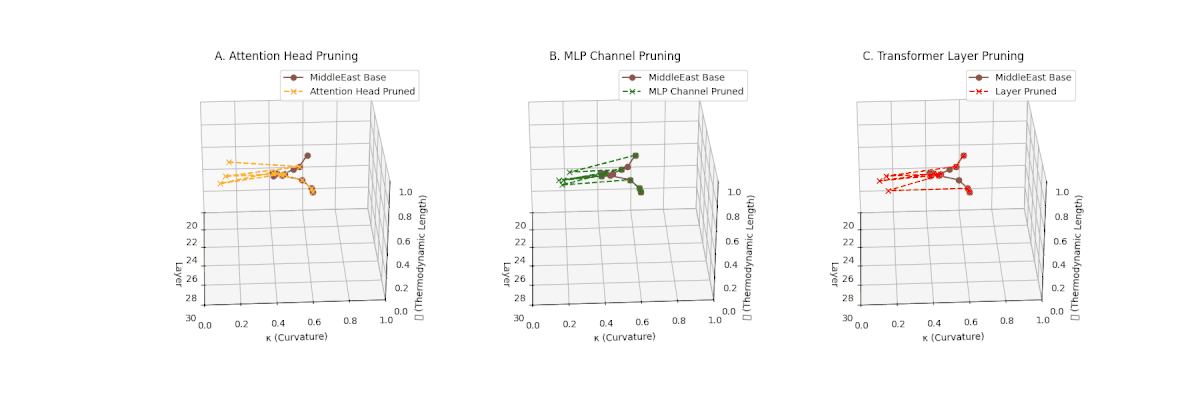
Three pruning strategy comparison plots for Middle East-tuned model — **Quantization + Pruning Effects on Middle East**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ $\approx 0.4$, $\kappa_\ell$ $\approx 0.3$. Partial loss. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ $\le 0.3$, $\kappa_\ell$ $\le 0.3$. Stronger collapse. **(C) Transformer Layer Pruning:** Deep collapse, $\mathcal{L}_\ell$ $\le 0.2$, $\kappa_\ell$ $\le 0.2$.

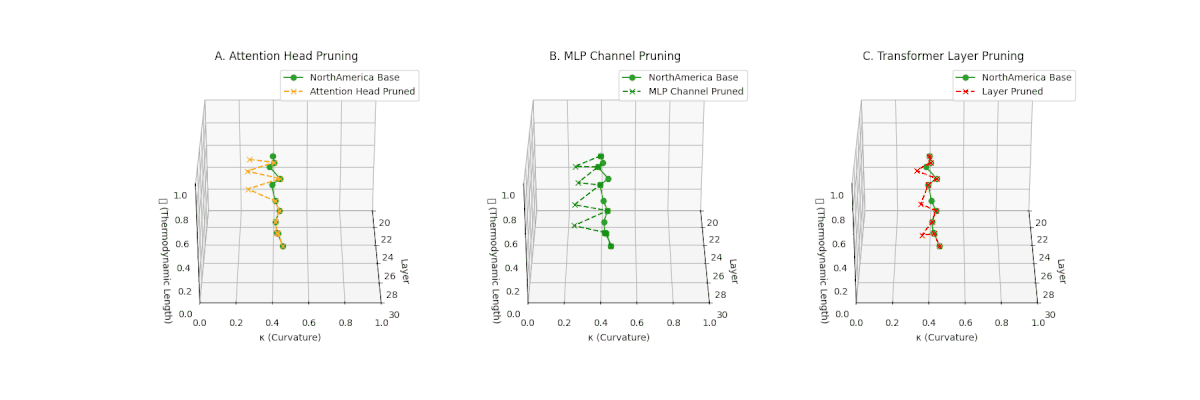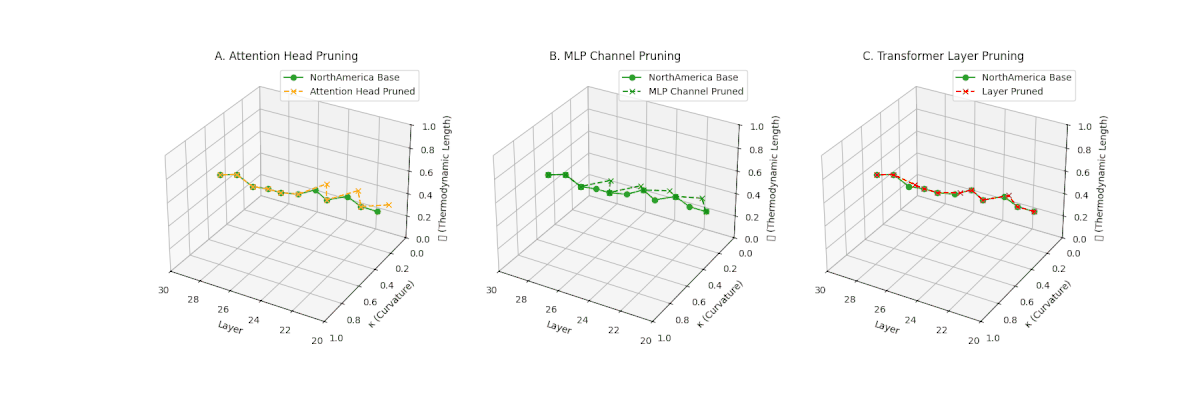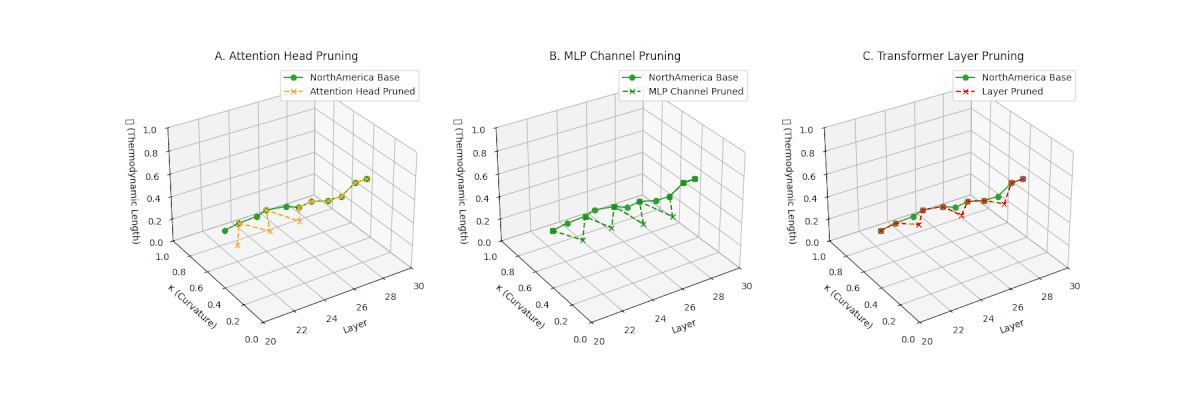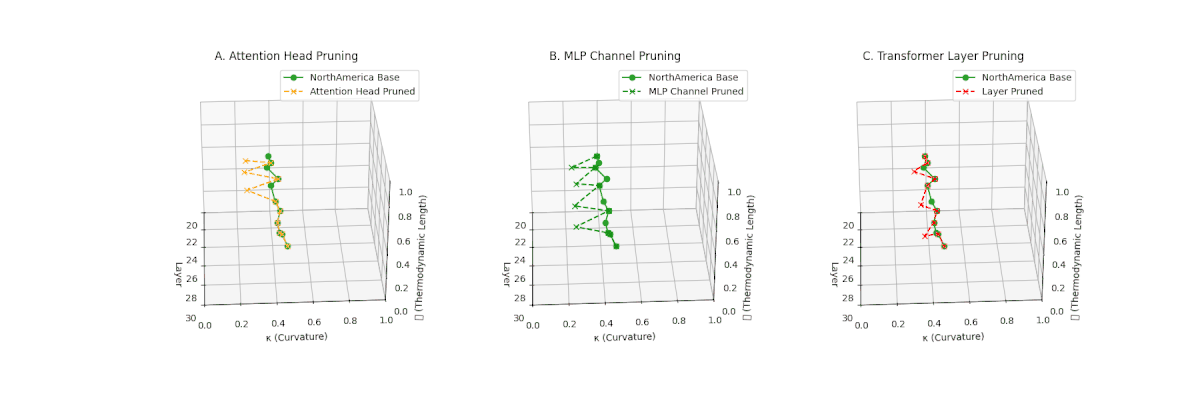
Three pruning strategy comparison plots for North America-tuned model — **Quantization + Pruning Effects on North America**
**(A) Attention Head Pruning:** $\mathcal{L}_\ell$ $\approx 0.4$, $\kappa_\ell$ $\approx 0.3$. Mild collapse. **(B) MLP Channel Pruning:** $\mathcal{L}_\ell$ $\le 0.3$, $\kappa_\ell$ $\le 0.3$. Significant latent path reduction. **(C) Transformer Layer Pruning:** Severe collapse, $\mathcal{L}_\ell$ $\le 0.2$, $\kappa_\ell$ $\le 0.2$.

Pruning-Induced Thermodynamic Collapse and Cultural Sensitivity. Transformer layer pruning consistently produces the strongest thermodynamic collapse across cultures ($\mathcal{L}_\ell \le 0.2$, $\kappa_\ell \le 0.2$), with MLP channel pruning as the next most damaging. Attention head pruning causes mild to moderate collapse ($\mathcal{L}_\ell \approx 0.4$, $\kappa_\ell \approx 0.3$). Culturally, Africa, Asia, and China suffer the deepest collapses, while Australia and North America exhibit comparatively resilient latent structures.

Analogy

Quantization as a Genome–Wide Hypomorph (nDNA View)

What we study. How uniform low-bit quantization reshapes a transformer’s epistemic manifold as read by the nDNA trio across depth: spectral curvature $\kappa_\ell$ (bending), thermodynamic length $L_\ell$ (epistemic work), and belief-field strength $\lVert\mathbf v^{(c)}_\ell\rVert$ (value/instruction steering).

Plain-language summary
Quantization does not cut out modules; it reduces resolution everywhere. The model often keeps the same answers, but the internal geometry that makes reasoning adaptable becomes shorter, straighter, and less guided.

Operator (what quantization does)

Let $W$ be a weight tensor (per layer/block groups). $b$-bit uniform quantization acts as

\[\widehat W=Q_b(W)=s\,\mathrm{round}\!\big(W/s\big), \qquad s=\alpha/2^{\,b-1},\]

so $\widehat W=W+\varepsilon$ with approximately zero-mean noise whose variance scales with $s^2$ (per-group scale $\alpha$). Second-order, GPTQ-like schemes choose $Q_b$ to minimize a local quadratic proxy of layer loss.

Information-geometry impact (why $L,\kappa,\lVert\mathbf v\rVert$ move)

Write $J^{(\ell)}=\partial h_\ell/\partial h_{\ell-1}$ and $J=\prod_{\ell} J^{(\ell)}$. With Fisher metric

\[F_\ell=\mathbb{E}\!\left[\nabla_{h_\ell}\log p_\theta(x)\,\nabla_{h_\ell}\log p_\theta(x)^\top\right],\]

quantization perturbs the Jacobian chain so that sensitivity along principal directions shrinks. In practice:

\[\widehat L_\ell \ \text{contracts}, \qquad \widehat\kappa_\ell \ \text{flattens (fine bends are damped)}, \qquad \lVert\widehat{\mathbf v}^{(c)}_\ell\rVert\ \text{weakens and aligns into a narrower cone}.\]

Chromosome-level analogy (clear mapping)

Weights → loci; layers/blocks → regulatory neighborhoods (TADs); scales/zero-points → chromatin accessibility.
Quantization ≡ genome-wide hypomorph. Every locus persists but its dynamic range is clipped; small variations fall below the noise floor. This is not a deletion (no module is excised), but a resolution squeeze—akin to mild chromatin compaction.
Intuition. The melody (task behavior) remains recognizable; the musical dynamics—crescendo, rubato, micro-timing—are flattened. In nDNA: bends diminish ($\kappa_\ell\downarrow$), paths shorten ($L_\ell\downarrow$), and the steering cone tightens ($\lVert\mathbf v^{(c)}_\ell\rVert\downarrow$).

Control & robustness (intuition first, math beneath)

Depth acts like a dynamical system transporting representations. The controllability Gramian $\Sigma_\ell$ indicates how many directions are reachable with finite “energy.” Quantization squeezes the singular spectrum of the Jacobian product $J$, so $\mathrm{tr}(\widehat\Sigma_\ell)$ falls: sharp turns become harder, the traversable path shortens, and value/instruction alignment exerts weaker guidance. Off-distribution adaptation degrades in proportion to the loss of principal Fisher directions.

Design guardrails (actionable, geometry-aware)

Bit-width by Fisher budget. Choose $b$ so the expected total drop in layerwise length $\sum_\ell (L_\ell-\widehat L_\ell)$ stays below a fixed fraction of $\sum_\ell L_\ell$.
Mixed precision for hotspots. Allocate more bits to layers with high $\kappa_\ell$ or large $\lVert\mathbf v^{(c)}_\ell\rVert$ (often late decision layers and culturally salient layers).
Second-order, group-wise calibration. Use GPTQ/LSQ-style grouping so the local quadratic error aligns with dominant singular directions; scale per-group step sizes to protect them.
Stochastic rounding & short post-quant tuning. Preserve small updates’ unbiasedness and briefly recalibrate on diverse prompts to restore belief-field alignment without overfitting.
Monitor a single scaffold score. Track $S_\ell=\kappa_\ell\,L_\ell\,\lVert\mathbf v^{(c)}_\ell\rVert$ across depth; a steady late-layer decline signals over-compression of reasoning geometry.

Key takeaways

Quantization is a resolution transform, not a surgical cut: it preserves phenotype while thinning morphology.
nDNA reveals a manifold that becomes shorter, straighter, and less guided unless bits are allocated where reasoning needs them most.
Simple guardrails—mixed precision on hotspots and a scaffold monitor—maintain adaptability with minimal footprint.

Pruning as Chromosomal Segment Deletion (nDNA View)

What we study. How three pruning regimes reshape a transformer’s epistemic manifold as read by nDNA across depth: spectral curvature $\kappa_\ell$ (bending), thermodynamic length $L_\ell$ (epistemic work), and belief-field strength $\lVert\mathbf v^{(c)}_\ell\rVert$ (value/instruction steering).

Plain-language summary
Pruning is not a tiny trim; it behaves like a chromosomal segment deletion. Entire co-adapted functions vanish together, breaking long-range coordination. The manifold that supports reasoning becomes shorter, kinked, and less steered.

Operator (what pruning does, abstractly)

Let $f_\theta$ have per-layer representations $h_\ell$ and Jacobians $J^{(\ell)}=\partial h_\ell/\partial h_{\ell-1}$, with chain $J=\prod_\ell J^{(\ell)}$. Pruning composes $f_\theta$ with a projection $P$ that removes coordinates/routes:

\[J^{(\ell)} \;\to\; J^{(\ell)} P \quad \text{(within a block)}, \qquad J \;\to\; \big(\prod_{k>\ell} J^{(k)}\big)\, \cancel{J^{(\ell)}} \,\big(\prod_{k<\ell} J^{(k)}\big) \quad \text{(block removal)}.\]

This lowers rank and squeezes the singular-value spectrum of $J$, thus reducing Fisher information, controllability, and the nDNA trio $(\kappa_\ell,L_\ell,\lVert\mathbf v^{(c)}_\ell\rVert)$.

Chromosome-level analogy (clear mapping)

Heads/channels/layers → genes/modules; blocks → regulatory neighborhoods (TADs); skip/attn routes → enhancer–promoter links.
Pruning ≡ copy-number loss (CNV deletion). A contiguous module is deleted; expression dosage and insulation collapse. Epistatic couplings vanish, so compensation routes fail.
nDNA phenotype. $L_\ell$ contracts (less work), $\kappa_\ell$ flattens or becomes piecewise (kinks), and $\lVert\mathbf v^{(c)}_\ell\rVert$ weakens or fans out (steering leakage).

Three pruning regimes

1) Attention-head pruning (route deletion). Criterion (gradient importance). For head $A^{(i)}$,

\[\mathcal I(A^{(i)}) \;=\; \mathbb E_{x}\,\big\|\nabla_{A^{(i)}} \mathcal L(x)\big\|, \qquad \text{prune if } \mathcal I(A^{(i)}) < \delta .\]

Graph view. Heads are edges in a routing multigraph. Deletions reduce algebraic connectivity (Laplacian $\lambda_2$), weakening global coordination.
nDNA fingerprint. Mid-layer $\kappa_\ell$ becomes spiky (non-$C^1$ turns), $\lVert\mathbf v^{(c)}\ell\rVert$ dips where stabilizing heads were removed; $L\ell$ shows local drops.

2) MLP-channel pruning (feature-palette deletion). Criterion (magnitude/LASSO). For channel $j$ with weight vector $w^{(j)}$,

\[\text{prune if } \ \lVert w^{(j)}\rVert_{1} < \epsilon \quad \text{or}\quad \min_{S}\ \lVert W-W_S\rVert^2 \ \text{s.t.}\ |S|\leq K \ \text{(structured selection)}.\]

Linearization. Multiplication by a projector $P$ drops singular values of $J^{(\ell)}$, shrinking $\mathrm{tr}\,F_\ell$ and thus $L_\ell$.
nDNA fingerprint. Steady $\kappa_\ell!\downarrow$ and $L_\ell!\downarrow$ across the pruned block; cultural separations blur (belief directions lose spread).

3) Transformer-layer pruning (block/segment deletion). Criterion (Fisher/gradient score). For block $\ell$,

\[\mathcal F^{(\ell)} \;=\; \mathbb E_x\!\left[\big\lVert\nabla_{\theta^{(\ell)}}\mathcal L(x)\big\rVert^2\right], \qquad \text{prune if } \mathcal F^{(\ell)} < \tau .\]

Depth dynamics. Removing a block discontinuously changes the depth connection; holonomy jumps, producing curvature/torsion discontinuities.
nDNA fingerprint. Global $L_\ell$ contraction across many layers, piecewise $\kappa_\ell$ (kinks), and broad weakening/divergence of $\mathbf v^{(c)}_\ell$ (steering leakage).

Information geometry & control (why robustness suffers)

With Fisher metric $F_\ell$ and controllability Gramian $\Sigma_\ell$ for the linearized depth dynamics, pruning reduces the reachable subspace: small singular modes vanish and $\mathrm{tr}(\Sigma_\ell)$ falls.
Intuition. Fewer well-conditioned directions $\Rightarrow$ harder to turn (lower $\kappa_\ell$), shorter paths to think (lower $L_\ell$), weaker compass to stay value-aligned (lower $\lVert\mathbf v^{(c)}_\ell\rVert$). Hence off-distribution adaptation degrades even if accuracy holds in-distribution.

Geometry fingerprints by scheme (at a glance)

Heads: local routing loss $\Rightarrow$ spiky $\kappa_\ell$, localized $L_\ell\downarrow$, steering dips near the removed heads.
Channels: palette narrowing $\Rightarrow$ smooth $\kappa_\ell\downarrow$, steady $L_\ell\downarrow$, cultural basins move closer (belief spread shrinks).
Layers: depth budget loss $\Rightarrow$ global $L_\ell\downarrow$, piecewise $\kappa_\ell$ (kinks), wide steering leakage (divergent belief flow).

Design guardrails (actionable, geometry-aware)

Head pruning with connectivity in mind. Preserve routing connectivity: avoid deletions that collapse the graph’s $\lambda_2$; re-inject tiny adapters where $\kappa_\ell$ becomes spiky.
Channel pruning with SV bounds. Constrain the singular-value tail removed from $J^{(\ell)}$; keep a floor on $\mathrm{tr}\,F_\ell$; revive concept-critical subspaces via small adapters.
Layer pruning with continuity checks. Require minimum Fisher and enforce $\kappa_\ell$ smoothness across surviving blocks; when depth is cut, budget extra $L_\ell$ via mild distillation on diverse prompts.
Monitor a single scaffold score. Track $S_\ell=\kappa_\ell\,L_\ell\,\lVert\mathbf v^{(c)}_\ell\rVert$; sustained late-layer decline indicates structural damage rather than benign sparsity.

Key takeaways

Pruning behaves like a CNV deletion: dosage drops and long-range coordination breaks.
nDNA reveals a manifold that is shorter ($L_\ell$), kinked or flattened ($\kappa_\ell$), and less steered ($\lVert\mathbf v^{(c)}_\ell\rVert$).
Geometry-aware criteria and a scaffold monitor help you keep speed-ups without destroying the model's internal ecology of reasoning.

Pruning a transformer is like a chromosomal segment deletion (large CNV loss) in a genome: you don’t just remove a single “gene,” you delete a contiguous block of co-adapted functions. When a whole layer or large block is pruned, the model suffers a dosage crash—many interacting “genes” (MLP channels, attention routes, normalization paths) disappear together—so upstream features lose their downstream consumers and downstream layers are starved of inputs. The phenotype matches your nDNA readouts: the model’s thermodynamic length (semantic work across depth) collapses, spectral curvature flattens or fragments as alternative routes vanish, and torsion/holonomy shows discontinuities where long-range coordination used to be. Just as CNV losses often break regulatory neighborhoods (TADs) and epistasis among genes, block pruning severs cross-layer couplings, so belief vectors lose directional coherence and drift. Severity depends on “genetic background”: in culturally specialized models the deleted segment carries niche programs with little redundancy, so the collapse is deeper; in more generalist models, parallel routes partly cushion the loss. In short, block/ layer pruning is a structural deletion—a large CNV—that reduces dosage, breaks coordination, and yields a systemic, geometry-level failure rather than a small, local tweak.

References

[1] Han, Song, Pool, Jeff, and others “Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding” arXiv preprint arXiv:1510.00149 (2015).

[2] Frankle, Jonathan and Carbin, Michael “The lottery ticket hypothesis: Finding sparse, trainable neural networks” ICLR (2019).

[3] Cheng, Yu, Wang, Duo, and others “Model compression and acceleration for deep neural networks: The principles, progress, and challenges” IEEE Signal Processing Magazine (2018).

[4] Nagel, Markus, Van Baalen, Mart, and others “Up or down? Adaptive rounding for post-training quantization” ECCV (2020).

[5] Zafrir, Ofir, Boudoukh, Guy, and others “Q8BERT: Quantized 8bit BERT” Fifth Workshop on Energy Efficient Machine Learning and Cognitive Computing (2019).

[6] Guo, Yitao, Pan, Ruize, and others “MLPrune: Multi-level pruning for transformer-based NLP models” arXiv preprint arXiv:2202.07036 (2022).

[7] Choukroun, Yoni, Kravchik, Evgenii, and others “Low-bit quantization of neural networks for efficient inference” ICCV Workshops (2019).

[8] Achille, Alessandro and Soatto, Stefano “Emergence of invariance and disentanglement in deep representations” The Journal of Machine Learning Research (2018).

[9] Mu, Jake and Andreas, Jacob “Compositional explanations of neuron activations in deep networks” NeurIPS (2020).

[10] Abid, Abubakar, Farooqi, Maheen, and others “Persistent anti-muslim bias in large language models” arXiv preprint arXiv:2101.05783 (2021).

[11] Bishop, John, Liao, Renjie, and others “Geometric lens on representation learning: Geodesics, curvature, and information flow in latent spaces” arXiv preprint arXiv:2302.01542 (2023).

[12] Wang, Siyu, Wang, Zirui, and others “What makes good in-context examples for GPT-3?” ICLR (2023).

[13] Frantar, Elias, Lin, Saleh, and others “GPTQ: Accurate post-training quantization for generative pre-trained transformers” Advances in Neural Information Processing Systems (2023).

[14] Dettmers, Tim, Pagnoni, Artidoro, and others “QLoRA: Efficient fine-tuning of quantized LLMs” Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (ACL) (2023).

[15] Gale, Trevor, Elsen, Erich, and others “The State of Sparsity in Deep Neural Networks” Proceedings of the 3rd MLSys Conference (2019). https://proceedings.mlsys.org/paper_files/paper/2019/file/2c601ad9e10b4a54803f4e389e7f39fa-Paper.pdf

[16] Michel, Paul, Levy, Omer, and others “Are sixteen heads really better than one?” Advances in Neural Information Processing Systems (NeurIPS) (2019).

[17] Voita, Elena, Talbot, David, and others “Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned” Proceedings of ACL (2019).

[18] Li, Hao, Kadav, Asim, and others “Pruning Filters for Efficient ConvNets” ICLR (2017).

[19] He, Yihui, Zhang, Xiangyu, and others “Channel pruning for accelerating very deep neural networks” Proceedings of the IEEE International Conference on Computer Vision (ICCV) (2017).

[20] Theis, Lucas, Shi, Weicheng, and others “Faster gaze estimation with dense networks and pruned landmarks” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2018).

[21] Ganesh, Jagadeesh, Chen, Zhi, and others “Compressing large-scale transformer-based models: A case study on BERT” Proceedings of the 6th Workshop on Deep Learning for Low-Resource NLP (DeepLo 2020) (2020).

nDNA - the Semantic Helix of Artificial Cognition

nDNA - the Semantic Helix of Artificial Cognition

BibTex

Lens - Quantization and Pruning as Thermodynamic Collapses

nDNA as a Lens: Quantization and Pruning as Thermodynamic Collapses

Pruning-Induced Epistemic Degeneration

Epistemic Degeneration

Formal Interpretation

Topological Interpretation

Experimental Setup

nDNA Interpretation

nDNA as a Diagnostic for Cognitive Loss

Analogy

Quantization as a Genome–Wide Hypomorph (nDNA View)

Operator (what quantization does)

Information-geometry impact (why $L,\kappa,\lVert\mathbf v\rVert$ move)

Chromosome-level analogy (clear mapping)

Control & robustness (intuition first, math beneath)

Design guardrails (actionable, geometry-aware)

Pruning as Chromosomal Segment Deletion (nDNA View)

Operator (what pruning does, abstractly)

Chromosome-level analogy (clear mapping)

Three pruning regimes

Information geometry & control (why robustness suffers)

Geometry fingerprints by scheme (at a glance)

Design guardrails (actionable, geometry-aware)

References