- Geometric Epistemic Modeling of Neural Organization for Zero-Shot Machine Translation Evaluation via nDNA

Micro-summary — details in the book

We present GENOME-MT (Geometric Epistemic Modeling of Neural Organization for Machine Translation Evaluation), a novel, generation-free framework for predicting zero-shot machine translation (MT) quality. Building on the emerging paradigm of neural genomics (nDNA), our approach conceptualizes translation difficulty through two foundational geometric quantities: semantic torsion — encoding the degree of *conceptual twisting between cross-lingual semantic manifolds — and epistemic force — quantifying the latent cognitive–geometric effort required to traverse between them.*

Abstract

We present GENOME-MT (Geometric Epistemic Modeling of Neural Organization for Machine Translation Evaluation), a novel, generation-free framework for predicting zero-shot machine translation (MT) quality. Building on the emerging paradigm of neural genomics (nDNA), our approach conceptualizes translation difficulty through two foundational geometric quantities: semantic torsion — encoding the degree of conceptual twisting between cross-lingual semantic manifolds — and epistemic force — quantifying the latent cognitive–geometric effort required to traverse between them.

We introduce the formal construct of Total Epistemic Effort, a unified metric that integrates semantic displacement and torsional complexity across the full transformer layer hierarchy. We demonstrate that this metric exhibits consistently strong correlations with standard MT evaluation measures, including BLEU, COMET, and chrF, even in extreme zero-resource regimes. Crucially, GENOME-MT requires no target-side decoding, enabling highly scalable, compute-efficient, and language-agnostic translation quality estimation.

Comprehensive experiments spanning typologically diverse language pairs (e.g., English–Hindi, English–Thai, English–Japanese) and heterogeneous model families (e.g., LLaMA, Mistral) empirically validate the predictive fidelity of our framework. These findings establish latent semantic geometry as a robust, interpretable, and deployment-ready proxy for linguistic transfer complexity, paving the way for pre-deployment diagnostics and principled resource allocation in multilingual NLP.

Editing the Semantic Genome: An nDNA Perspective on Machine Translation

Just as genetic engineering seeks to alter the blueprint of life by manipulating the sequence and structure of DNA, cross-lingual transfer in machine translation can be viewed as the editing of a semantic genome—a structured code of meaning embedded within the latent spaces of multilingual models. In this view, each language possesses a unique neural DNA (nDNA) signature, expressed through its spectral curvature, thermodynamic length, and belief vector field. Translating between two languages thus becomes a problem of transforming one high-dimensional manifold into another, a process governed not only by the magnitude of semantic displacement but also by the torsional misalignment of their epistemic trajectories. By quantifying these geometric and directional forces, we treat translation as the precise splicing, realignment, and recombination of semantic sequences—an operation whose difficulty can be measured without ever generating a single word.

Problem Setup: Latent Translation Without Decoding

Let $M$ denote a large language model (e.g., LLaMA, Mistral), and let $L_s$ and $L_t$ represent the source and target languages, respectively. Conventional MT evaluation relies on generating translations $\mathbf{y}_t$ from inputs $\mathbf{x}_s$ and scoring them (e.g., BLEU, COMET). Our goal is to estimate zero-shot translation quality for $(L_s \to L_t)$ without generating translations, by analyzing latent representational geometry.

Let $H^{(\ell)}_L$ denote the mean-pooled hidden states of language $L$ at transformer layer $\ell$, extracted from a corpus $X(L)$. We define the nDNA signature of $L$ at layer $\ell$ as:

\[\text{nDNA}^{(\ell)}(L) = \left( \kappa^{(\ell)}(L),\; L^{(\ell)}(L),\; v^{(\ell)}(L) \right),\]

where:

$\kappa^{(\ell)}(L)$ — spectral curvature: local manifold bending.
$L^{(\ell)}(L)$ — thermodynamic length: cumulative epistemic shift across layers.
$v^{(\ell)}(L)$ — belief vector: average update direction in latent semantic space.

Spectral Curvature

We measure curvature using PCA over hidden state covariance:

\[\kappa^{(\ell)}(L) = \frac{\sum_{i=1}^k \lambda^{(\ell)}_i}{\sum_{i=1}^d \lambda^{(\ell)}_i}, \quad k \ll d,\]

where $\lambda^{(\ell)}_i$ are eigenvalues of the covariance matrix.
Alternatively, curvature can be estimated via local Jacobian norms:

\[\kappa^{(\ell)}(L) \approx \mathbb{E}_{x \sim L} \left[ \frac{\|\nabla_x h^{(\ell)}(x)\|_F^2}{\|h^{(\ell)}(x)\|^2} \right].\]

The interlingual curvature difference is:

\[\Delta\kappa^{(\ell)} = \left| \kappa^{(\ell)}(L_s) - \kappa^{(\ell)}(L_t) \right|.\]

Thermodynamic Length

The thermodynamic length measures representational travel distance:

\[L^{(\ell)}(L) = \mathbb{E}_{x \sim L} \left[ \sum_{i=1}^{\ell} \|h^{(i)}(x) - h^{(i-1)}(x)\|_2 \right].\]

The divergence between languages is:

\[\Delta L^{(\ell)} = \left| L^{(\ell)}(L_s) - L^{(\ell)}(L_t) \right|.\]

To ensure scale invariance:

\[\widetilde{L}^{(\ell)}(L) = \frac{L^{(\ell)}(L)}{\mathbb{E}_{x \sim L} \|h^{(0)}(x)\|}.\]

Belief Vector Field and Semantic Torsion

The belief vector is defined as:

\[v^{(\ell)}(L) = \mathbb{E}_{x \sim L} \left[ h^{(\ell)}(x) - h^{(\ell-1)}(x) \right].\]

The semantic torsion angle is:

\[\theta^{(\ell)} = \arccos \left( \frac{\langle v^{(\ell)}(L_s), v^{(\ell)}(L_t) \rangle}{\|v^{(\ell)}(L_s)\| \cdot \|v^{(\ell)}(L_t)\|} \right).\]

The epistemic force at layer $\ell$ is:

\[F^{(\ell)} = \Delta\kappa^{(\ell)} \cdot \Delta L^{(\ell)} \cdot \sin \theta^{(\ell)}.\]

Total Epistemic Effort

The total epistemic effort aggregates mismatch, drift, and belief-vector deviation:

\[E_{\text{total}} = \sum_{\ell=1}^L \omega^{(\ell)} \cdot \Delta\kappa^{(\ell)} \cdot \Delta L^{(\ell)} \cdot \|v^{(\ell)}(L_s) - v^{(\ell)}(L_t)\|,\]

where $\omega^{(\ell)}$ are layer weights (e.g., heuristic or learned).
We find:

\[\widehat{\text{BLEU}}(L_s \to L_t) \propto \frac{1}{E_{\text{total}}},\]

enabling scalable, pre-deployment MT quality estimation without decoding or references.

nDNA River Plots: Cross-Lingual Semantic Drift Trajectories

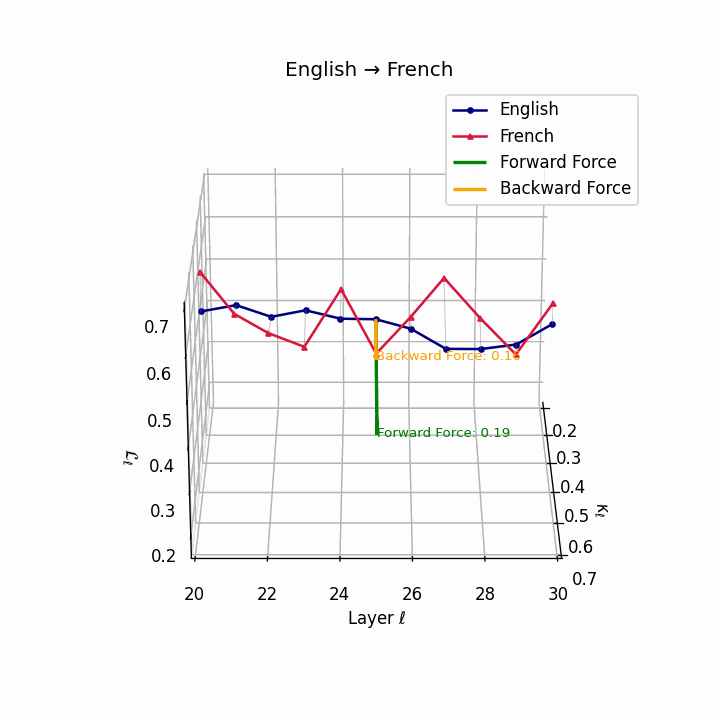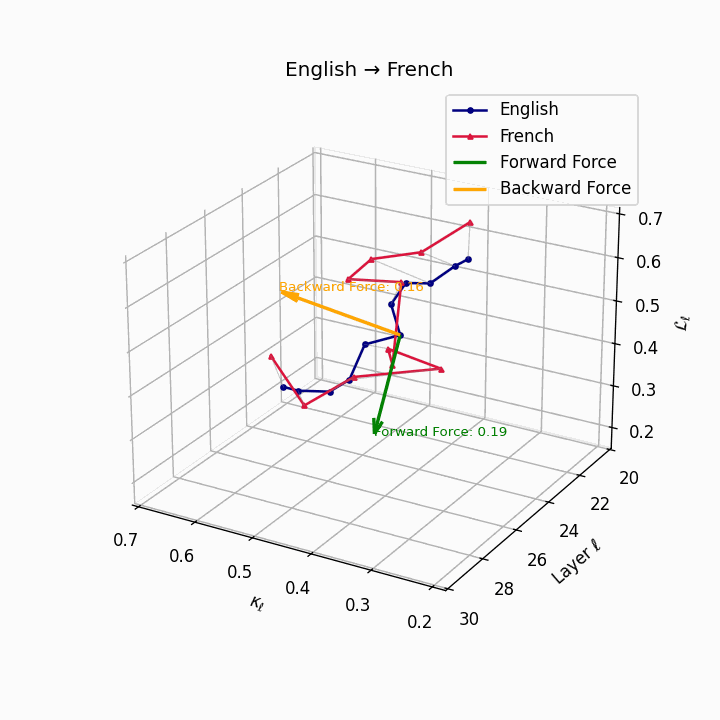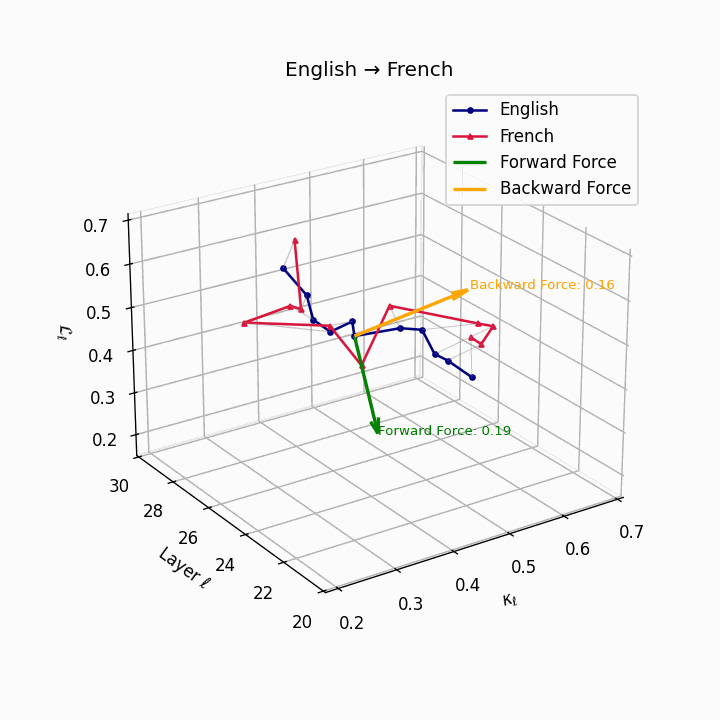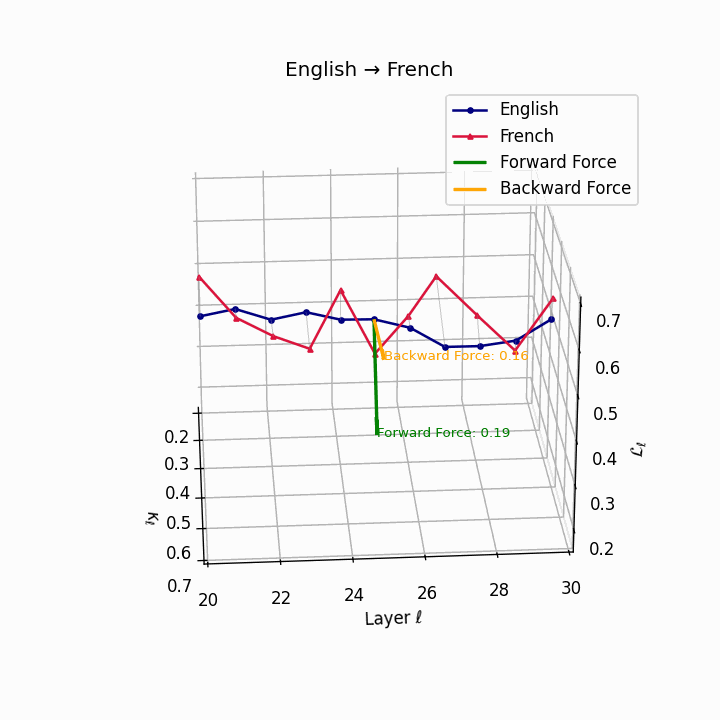
**English → French**: nDNA river plot showing semantic drift trajectories across transformer layers. Blue represents English semantic evolution, red represents French evolution. The close alignment indicates minimal epistemic effort required for translation.

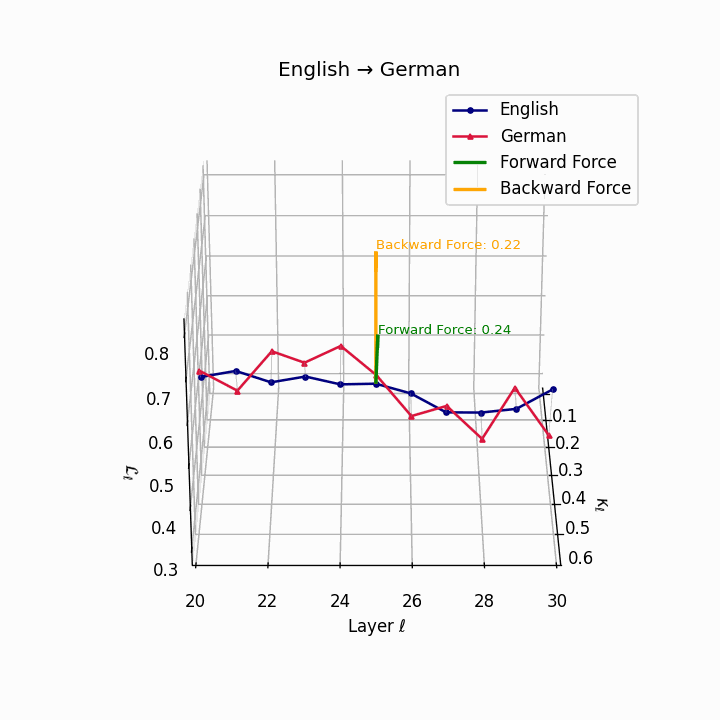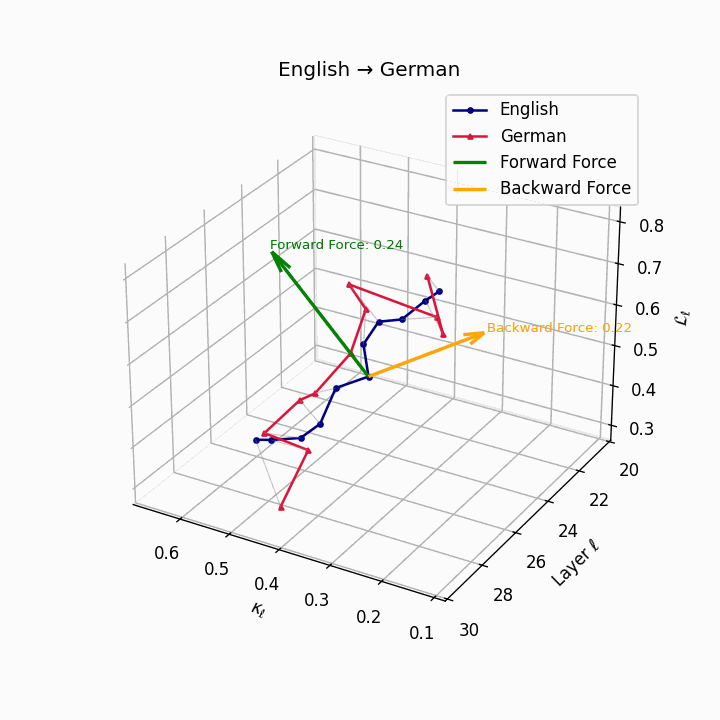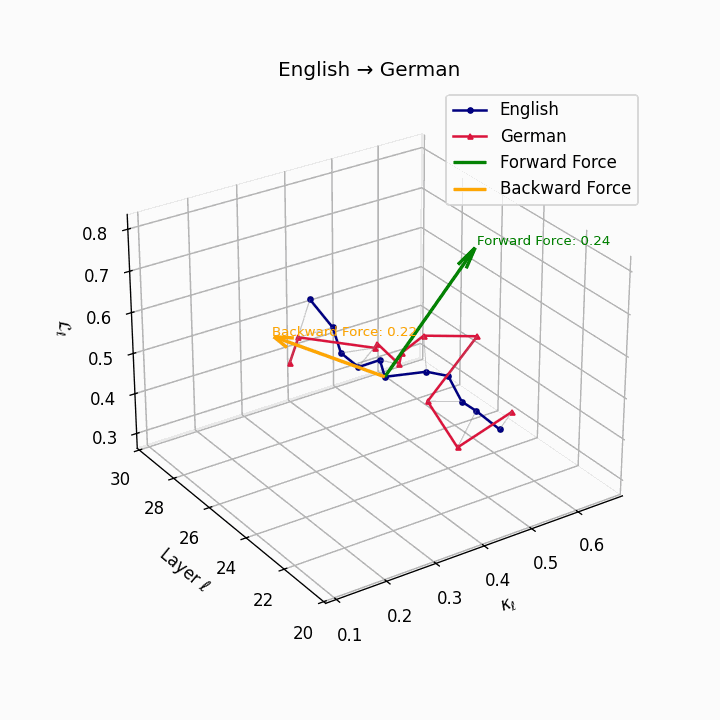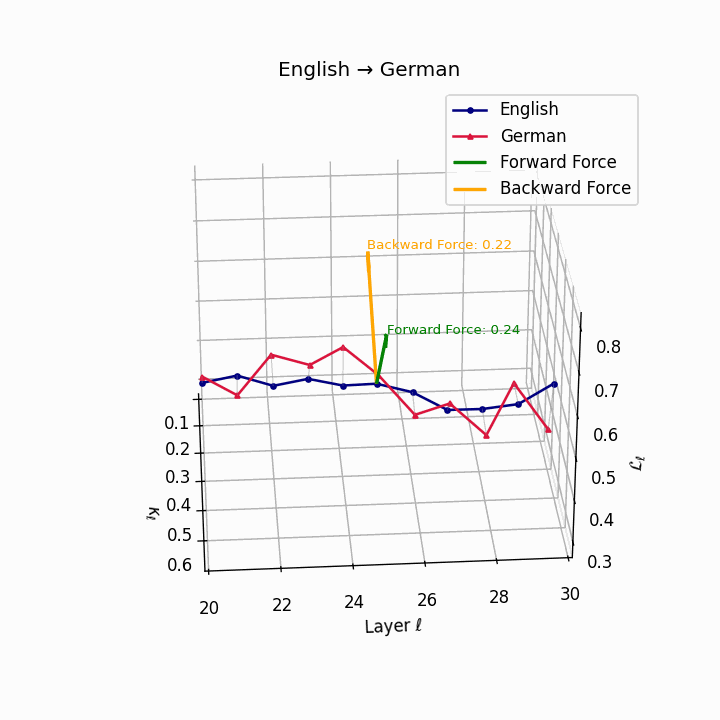
**English → German**: Semantic trajectories showing moderate divergence due to German’s case-marking system and verb-second placement, requiring higher epistemic effort than Romance languages.

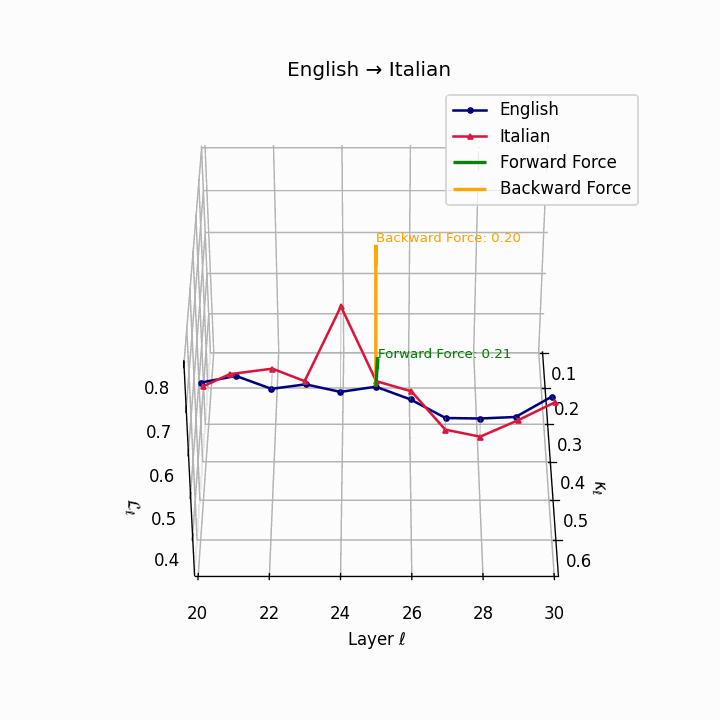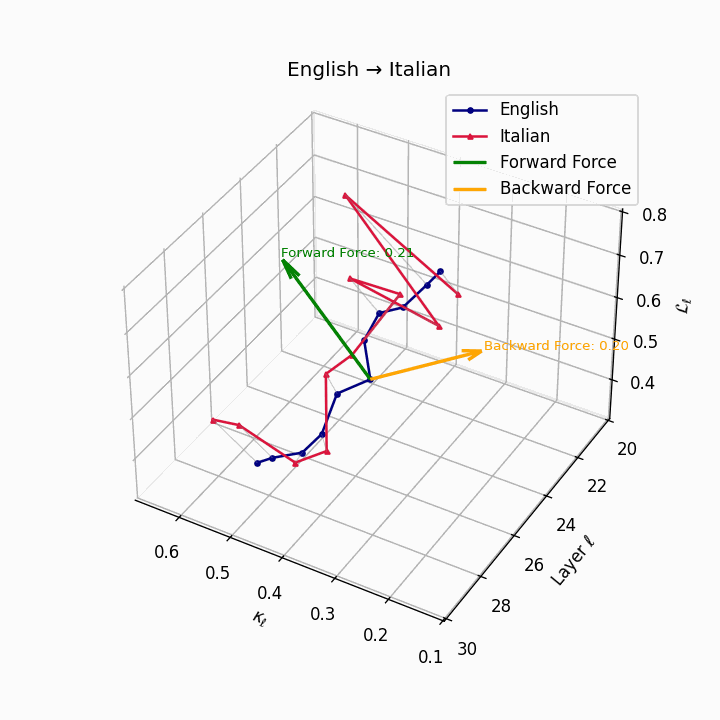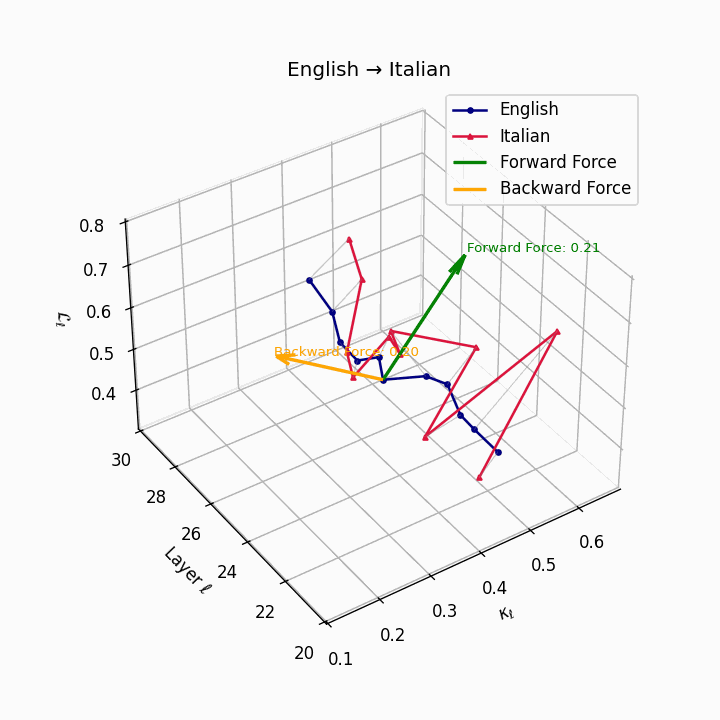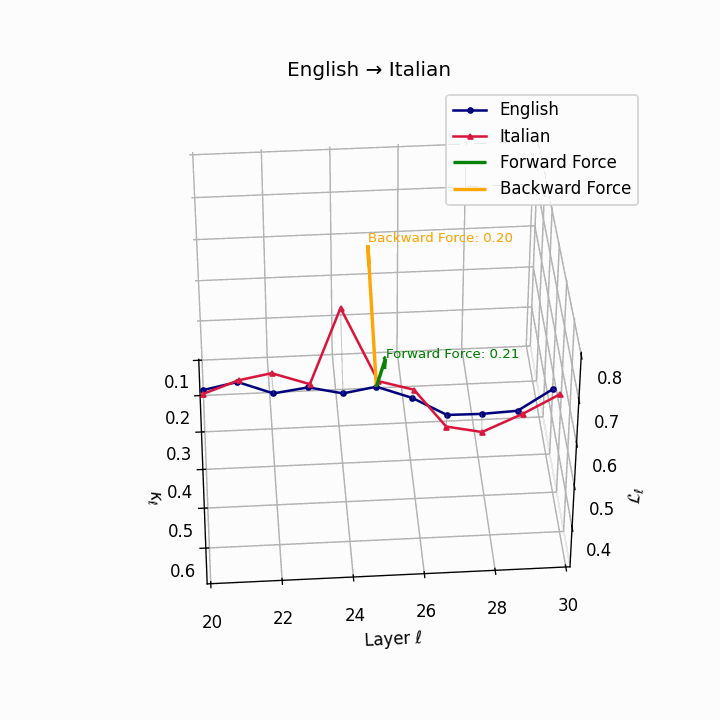
**English → Italian**: Close semantic alignment reflecting shared SVO structure and low torsional complexity between the language manifolds.

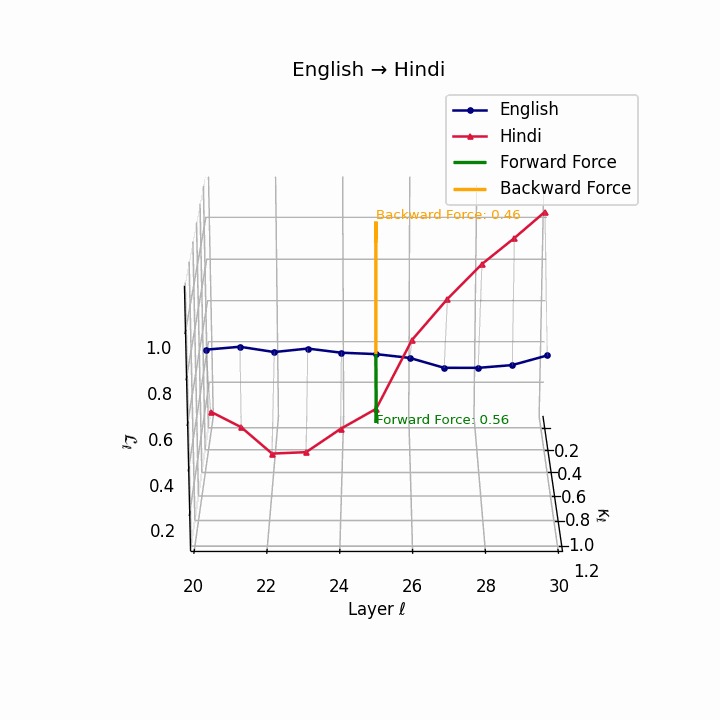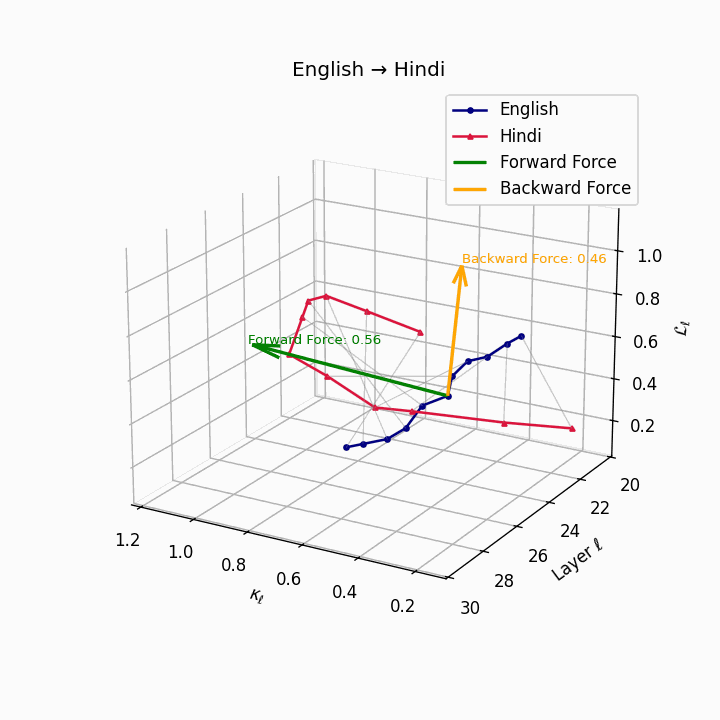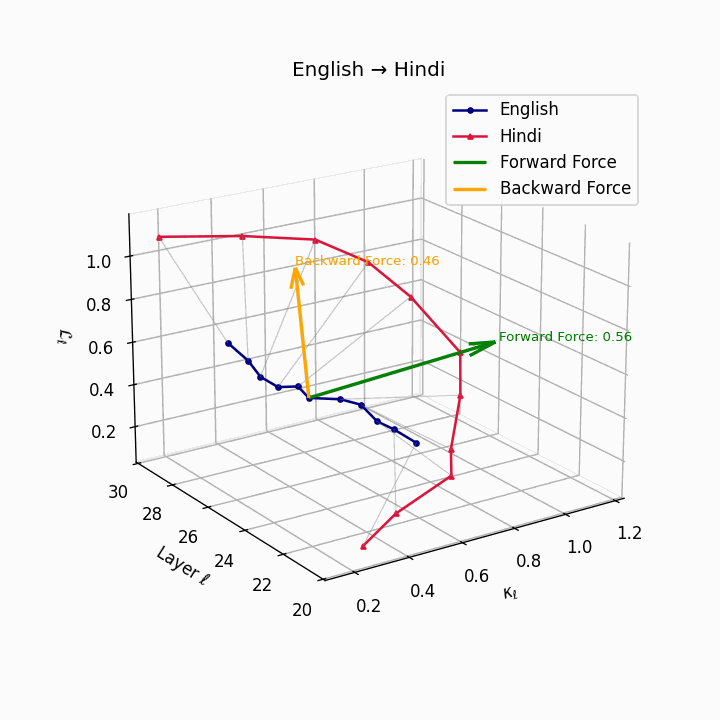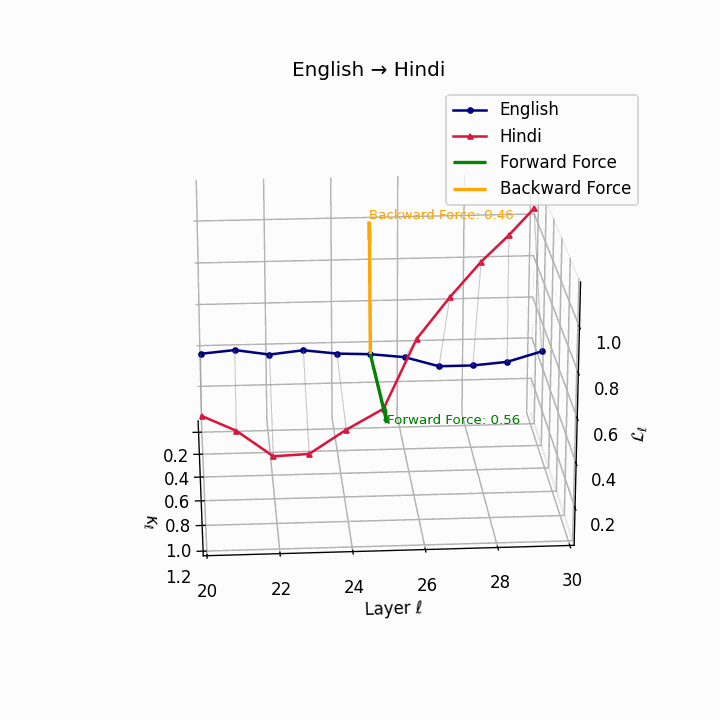
**English → Hindi**: Increased semantic divergence visible in the trajectories, reflecting SOV word order, morphological complexity, and script differences requiring moderate epistemic effort.

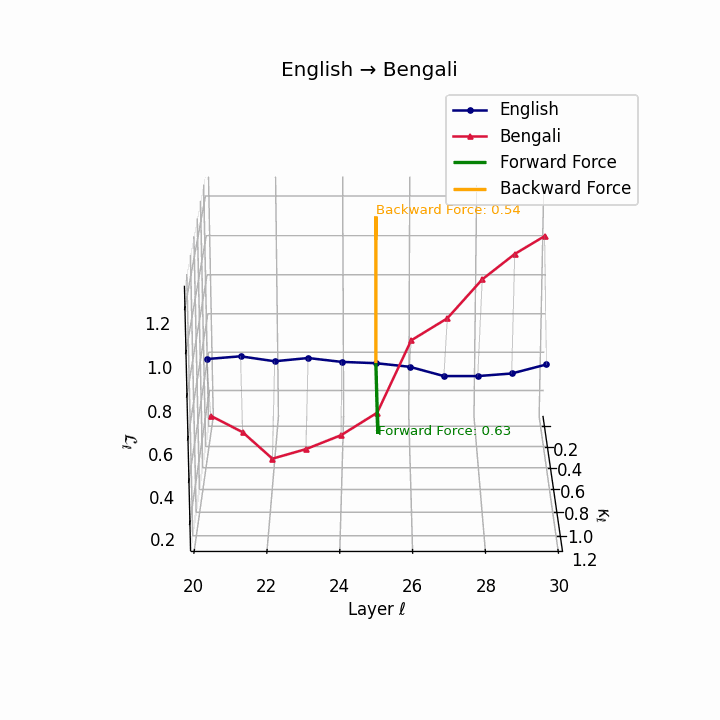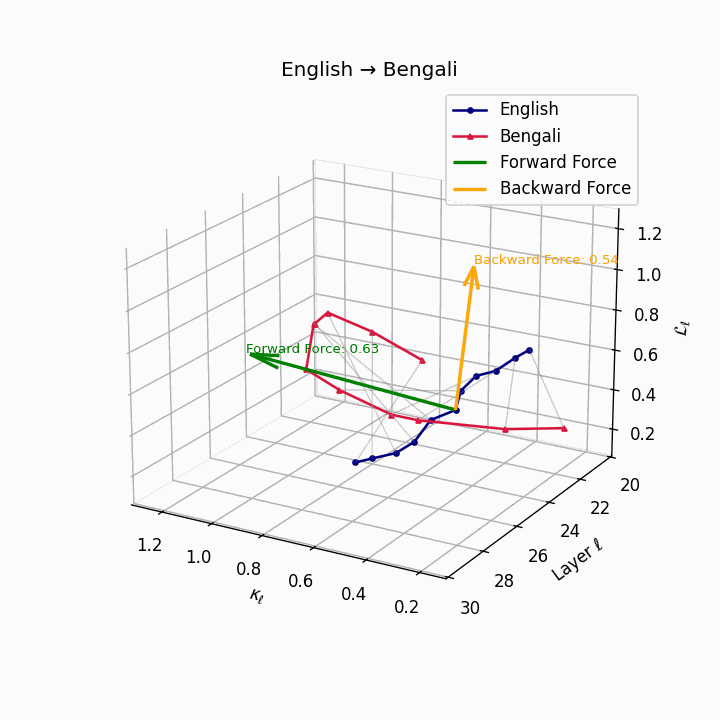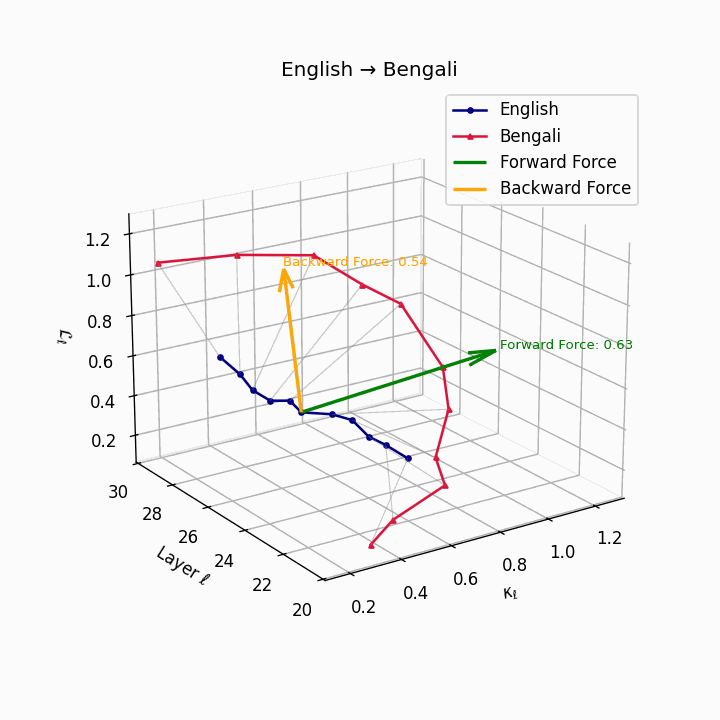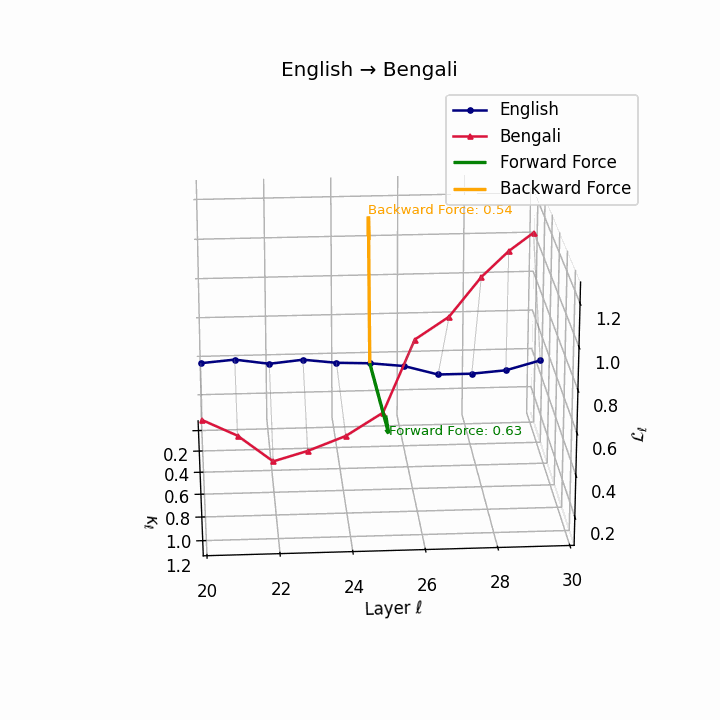
**English → Bengali**: Semantic drift patterns showing compound verb structures and lexicosyntactic shifts that contribute to translation difficulty.

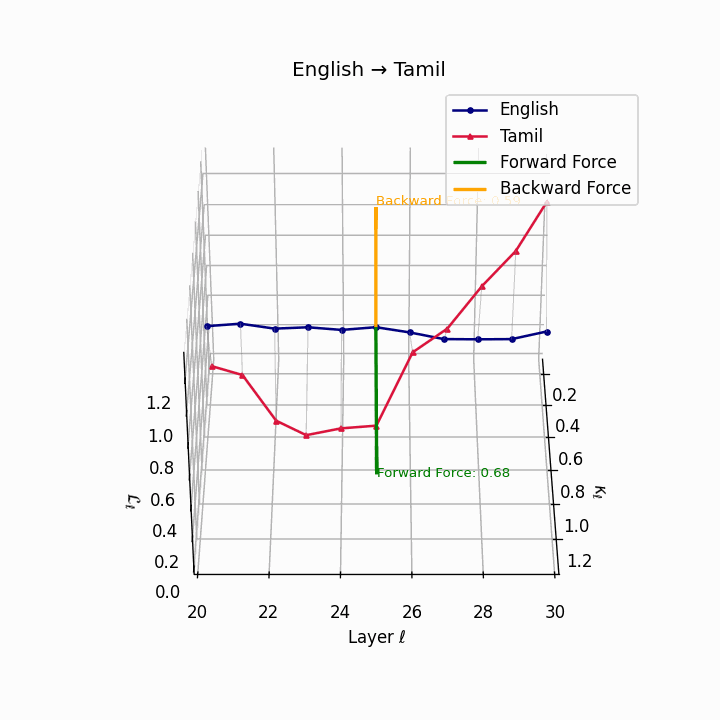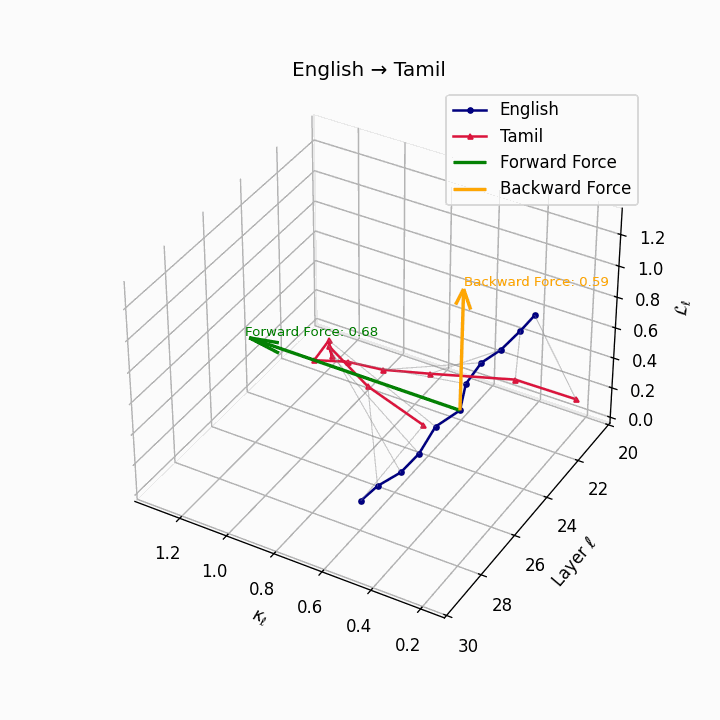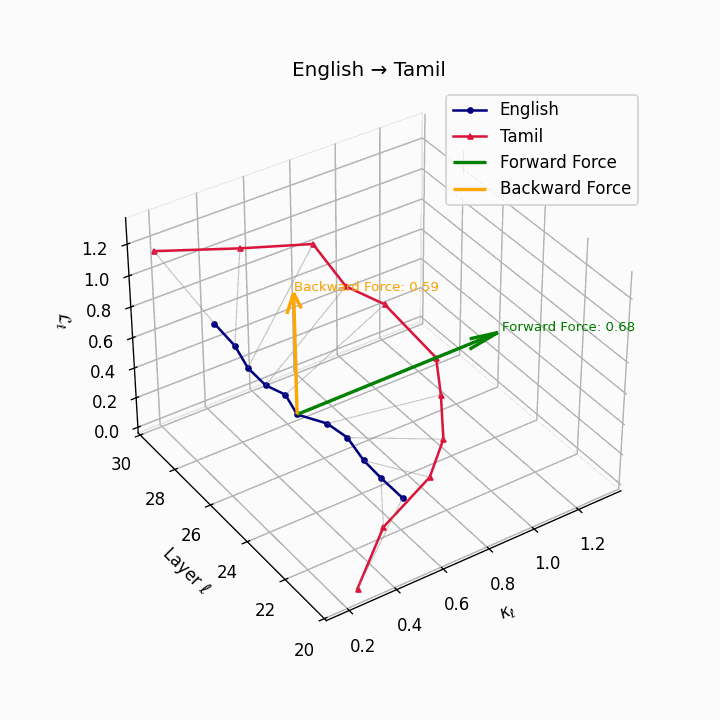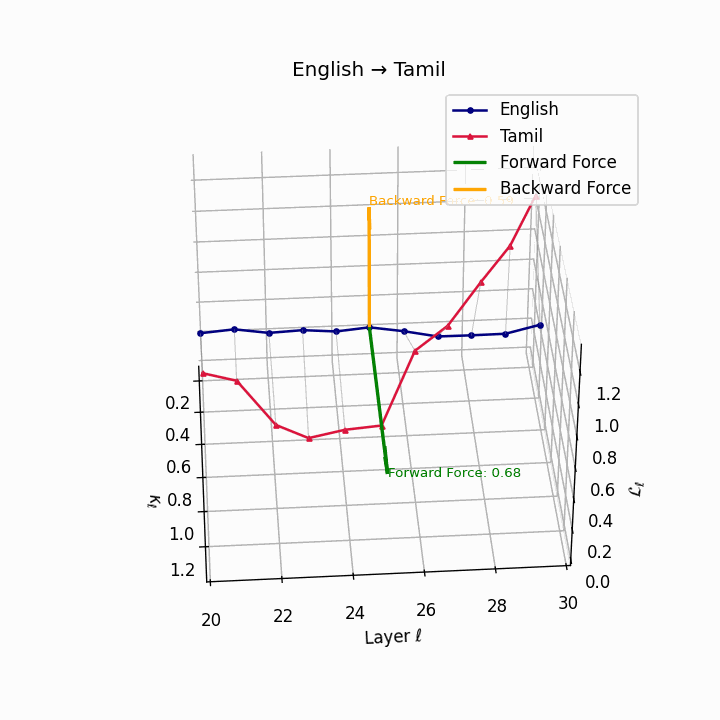
**English → Tamil**: Substantial trajectory divergence reflecting agglutinative Dravidian structure and typological distance from English.

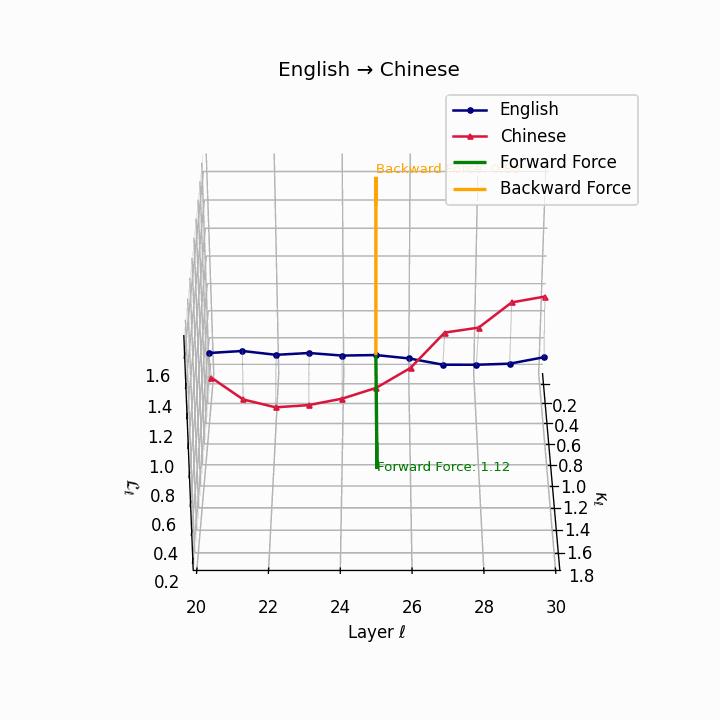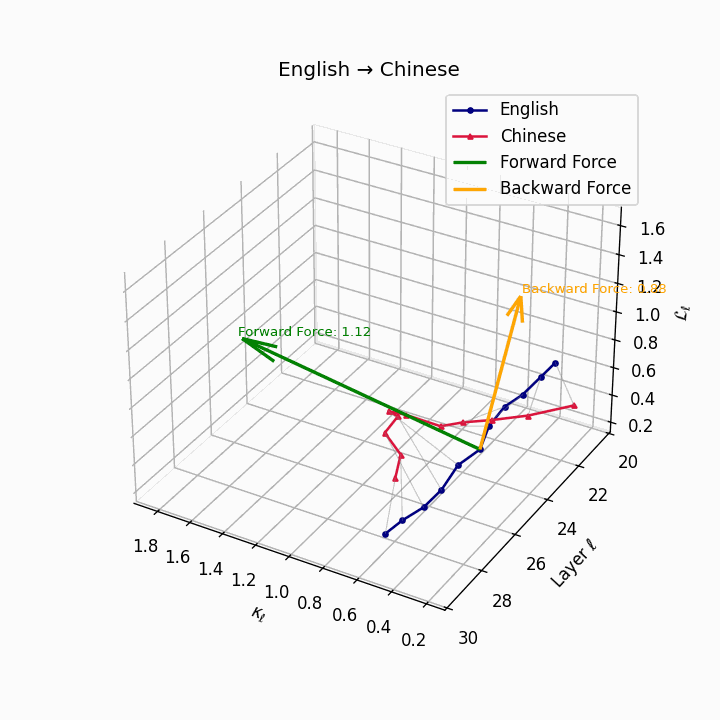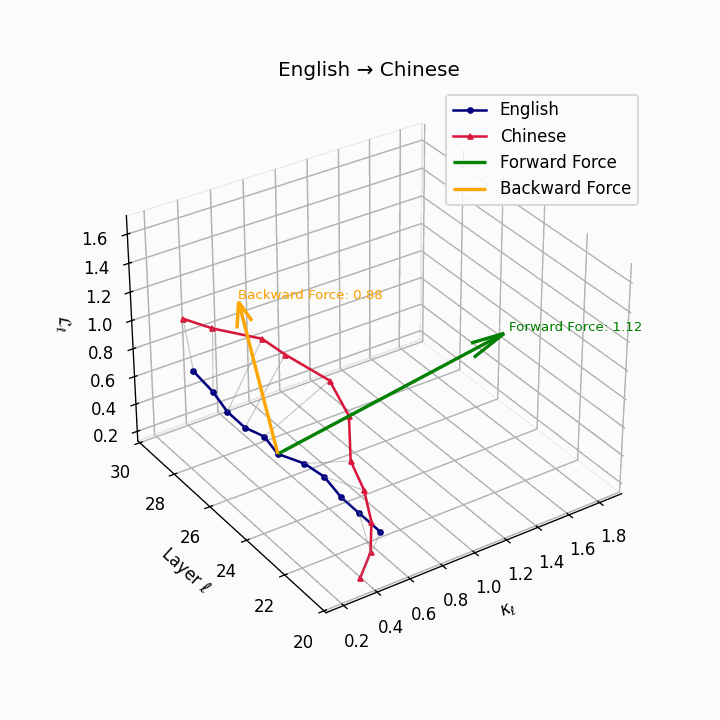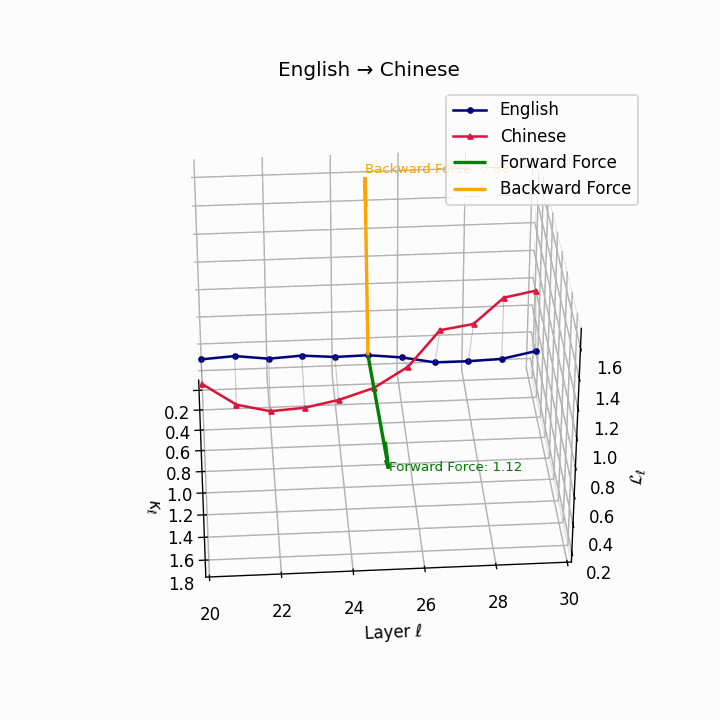
**English → Chinese**: High semantic divergence due to tonal systems, aspectual differences, and absence of case markers, requiring significant epistemic effort.

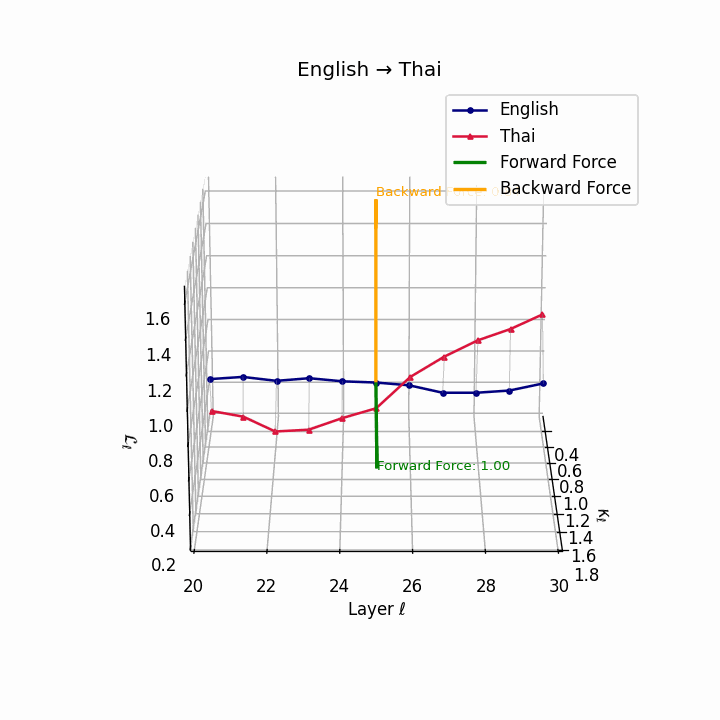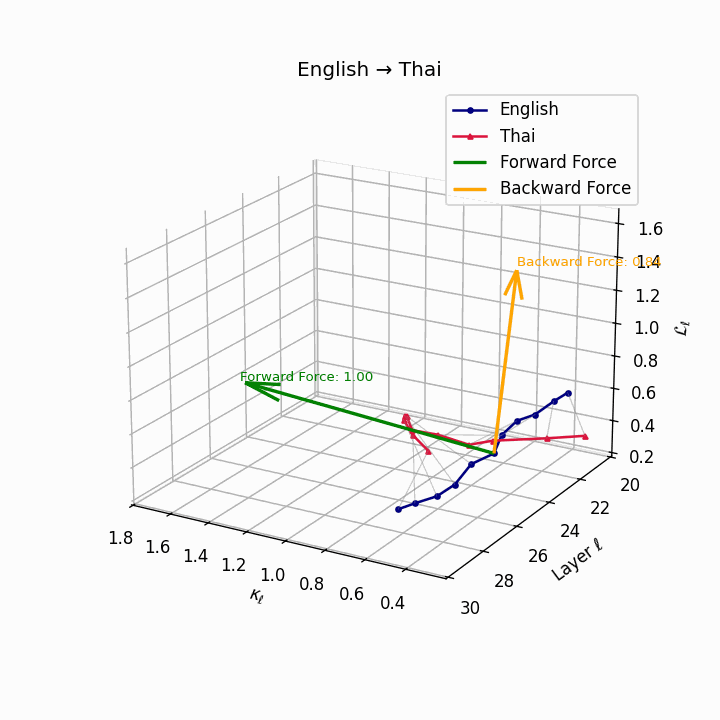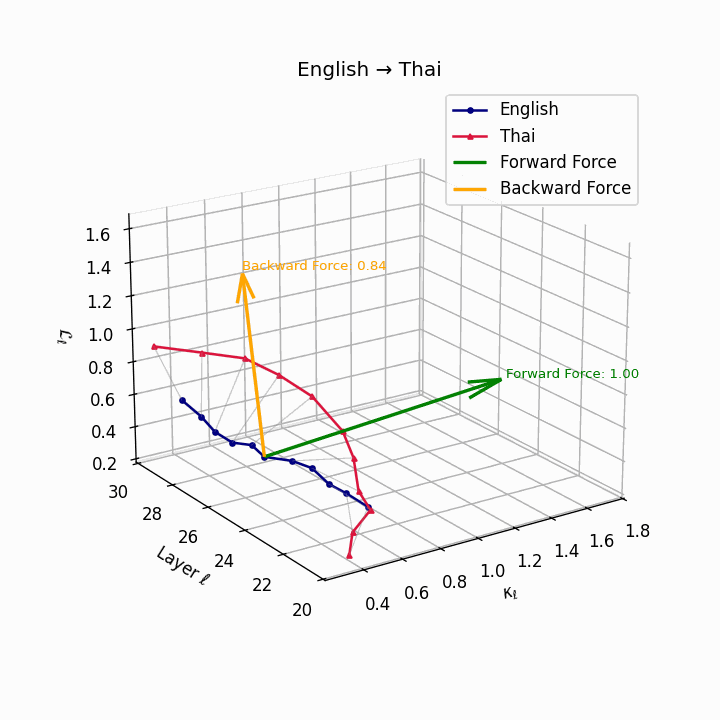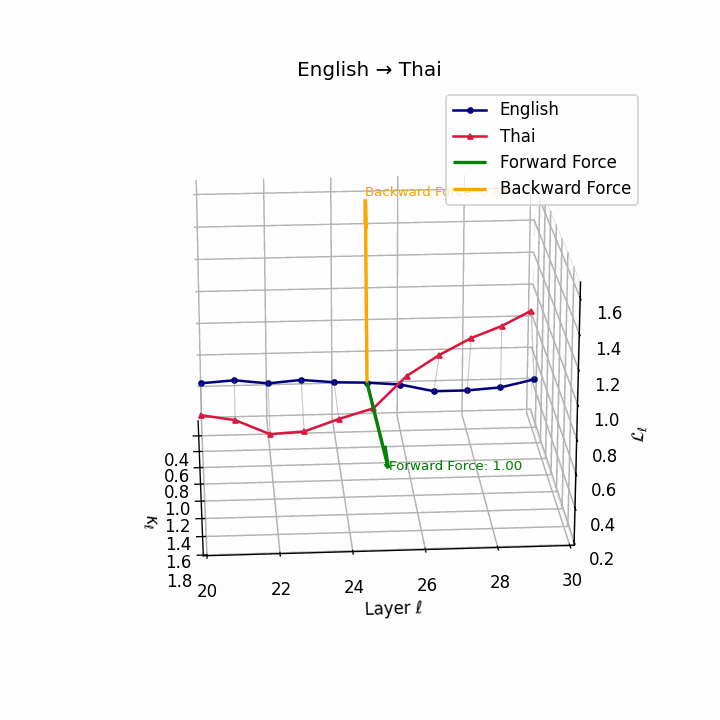
**English → Thai**: Classifier systems and tonal mismatch create substantial geometric distance between language manifolds despite SVO similarity.

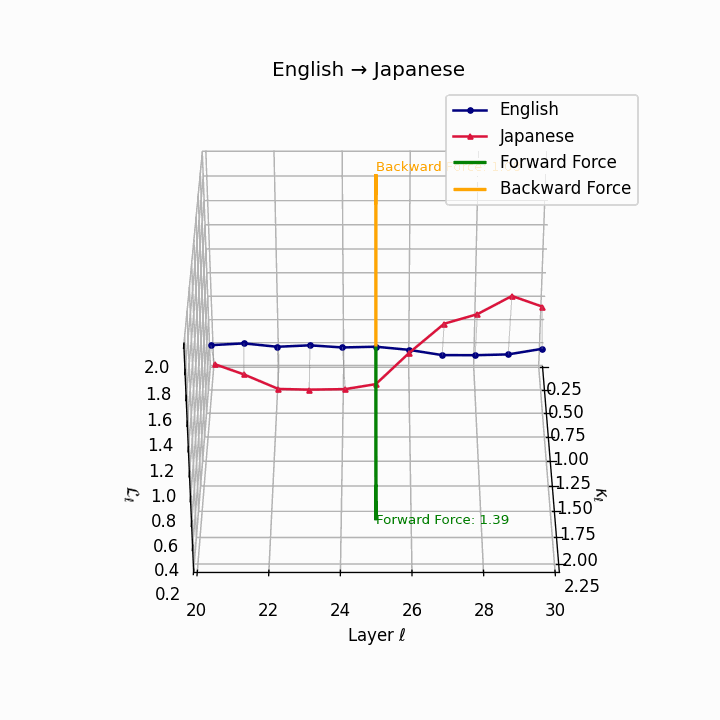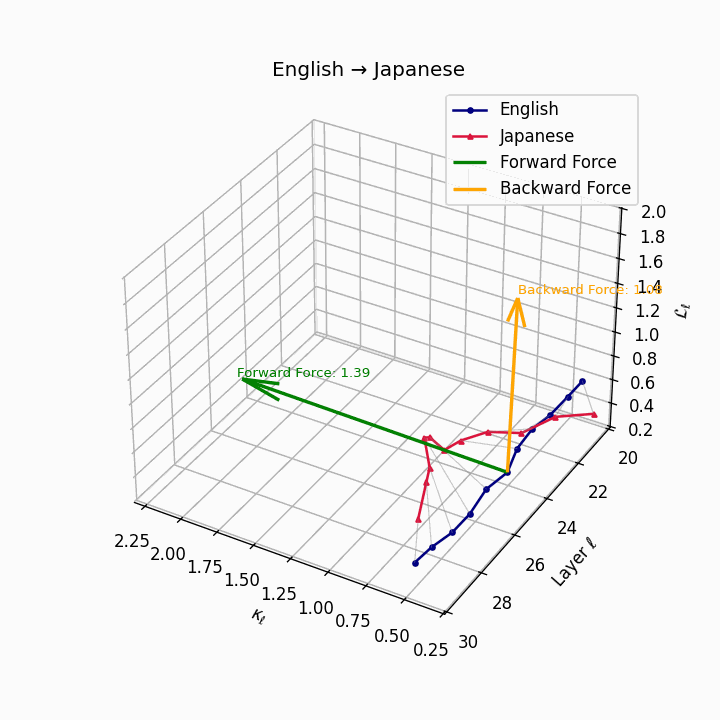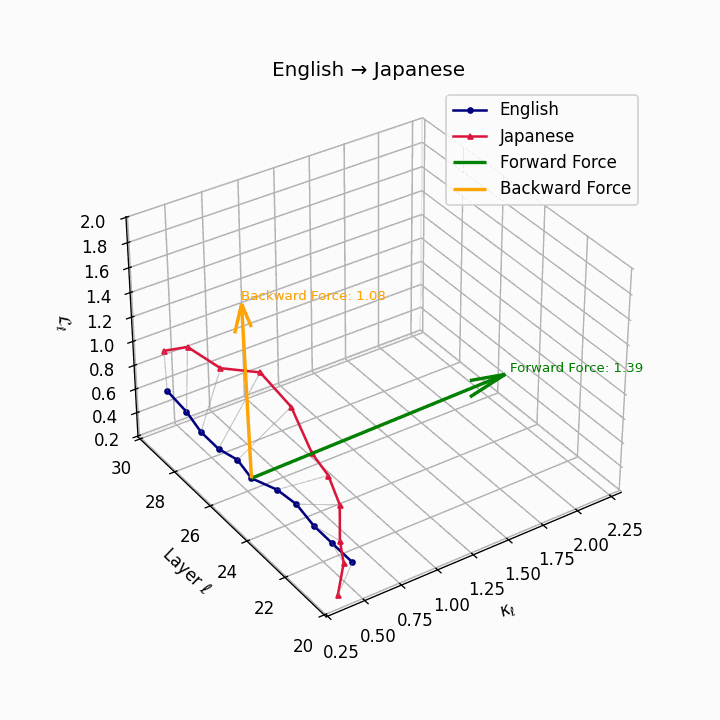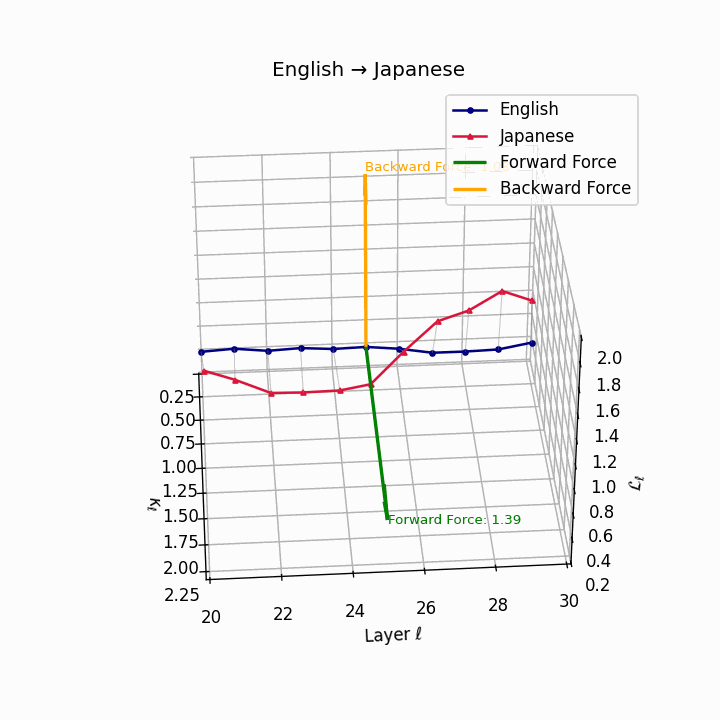
**English → Japanese**: Maximum semantic divergence observed, reflecting topic-prominence, scrambling, and honorific complexity creating the highest epistemic barriers.

Summary of Results

We begin our analysis by examining the relationship between structural divergence—captured via distance (Dist) and torsion (Torsion) metrics—and machine translation quality as measured by BLEU [1]. The results span eight typologically diverse target languages, covering a continuum from closely related Indo-European languages (French, German, Italian) to morphologically rich and script-divergent languages (Hindi, Bengali, Tamil) and finally to typologically distant East and Southeast Asian languages (Chinese, Thai, Japanese).

Translation Difficulty Correlates with Structural Divergence
Language pairs with low Dist and low Torsion (e.g., French, German, Italian) achieve the highest BLEU scores (≈38–42) in both directions. These languages share SVO word order and relatively similar analytic structures with English, requiring minimal reordering [2][3].
Morphologically Rich and Script-Divergent Languages Show Moderate Drops
Hindi, Bengali, and Tamil have mid-range Dist/Torsion values (0.44–0.50 Dist, 0.27–0.35 Torsion), leading to BLEU scores in the mid-20s. Contributing factors include SOV order, compound verbs, lexicosyntactic shifts, and agglutinative morphology [4][5][6]. From a biological systems perspective, these changes resemble mid-level structural rearrangements in genetic material that alter function without fully breaking systemic compatibility [7][8].
Typologically Distant Languages Are the Hardest
Chinese, Thai, and Japanese have the highest Dist/Torsion values (up to 0.81 Dist, 0.72 Torsion) and the lowest BLEU scores (13–20). Structural differences include tonal systems, classifier-based syntax, topic-prominence, and scrambling, combined with the absence of case markers or differing alignment strategies [9][10]. In biological analogy, this reflects large-scale genome rearrangements or cross-species divergence, where functional translation requires overcoming profound structural incompatibilities [11][7].
Strong Negative Correlation Between Structural Divergence and BLEU
Pearson correlation between total error $\mathcal{E}_{\text{total}}$ and BLEU shows robust relationships:
- English → Target: $\rho = -0.91$
- Target → English: $\rho = -0.89$
Spearman rank correlations are similarly strong (≈-0.91 to -0.93), indicating a robust monotonic relationship between divergence metrics and translation quality, consistent with prior findings that increased linguistic and structural distance predicts reduced cross-lingual transfer efficiency [12][13].

Directional Total Epistemic Effort $\mathcal{E}_{\text{total}}$ vs BLEU Score for Zero-Shot Machine Translation. Each block shows the forward $\texttt{En→X}$ and reverse $\texttt{X→En}$ scores together.

Language Pair	English → Target				Target → English				Linguistic Commentary
	Dist	Torsion	$\mathcal{E}_{\text{total}}$	BLEU	Dist	Torsion	$\mathcal{E}_{\text{total}}$	BLEU
French	0.18	0.06	0.19	41.8	0.15	0.04	0.16	43.5	Minimal reordering, analytic structure.
German	0.22	0.08	0.24	38.6	0.20	0.07	0.22	39.7	Case-marking + verb-second placement.
Italian	0.20	0.07	0.21	40.1	0.18	0.06	0.20	41.3	Shared SVO structure, low torsion.
Hindi	0.44	0.27	0.56	26.1	0.39	0.21	0.46	28.4	SOV order, script and morphological divergence.
Bengali	0.48	0.31	0.63	24.8	0.42	0.26	0.54	26.7	Compound verbs, lexicosyntactic shifts.
Tamil	0.50	0.35	0.68	23.2	0.43	0.29	0.59	25.6	Agglutinative Dravidian structure; distant typology.
Chinese	0.71	0.58	1.12	16.4	0.61	0.44	0.88	18.9	Tonal and aspectual systems; no case markers.
Thai	0.67	0.49	1.00	18.2	0.59	0.38	0.84	20.5	Classifier system, tone mismatch, SVO similarity.
Japanese	0.81	0.72	1.39	13.5	0.69	0.55	1.08	16.2	Topic-prominence, scrambling, honorific complexity.

Correlation Analysis:

Pearson Correlation (En→Target): $\rho = -0.91$
Pearson Correlation (Target→En): $\rho = -0.89$
Spearman Rank (En→Target): $-0.93$
Spearman Rank (Target→En): $-0.91$

Conclusion and Outlook

This study establishes a clear and quantifiable link between structural divergence—captured through Dist and Torsion—and zero-shot machine translation quality. Languages structurally closer to English (e.g., French, German, Italian) exhibit high BLEU scores with minimal epistemic effort, while morphologically rich or script-divergent languages (e.g., Hindi, Bengali, Tamil) show moderate performance drops. Typologically distant languages (e.g., Chinese, Thai, Japanese) present the most significant challenges, underscoring the impact of deep syntactic, morphological, and alignment differences on translation performance.

Beyond descriptive correlation, our findings highlight structural divergence metrics as a robust predictor of cross-lingual transfer difficulty. The strong negative Pearson ($\rho \approx -0.90$) and Spearman ($\rho \approx -0.92$) correlations suggest that these metrics could serve as pre-training indicators for MT system design, enabling resource allocation to languages where structural divergence imposes the greatest epistemic burden.

Outlook

Future work can extend this framework in three key directions:

Dynamic adaptation—integrating divergence-aware token reordering and morphological decomposition into the model architecture
Low-resource enhancement—leveraging synthetic parallel corpora informed by structural metrics to bootstrap under-represented language pairs
Generalization beyond MT—applying the Dist+Torsion paradigm to other multilingual NLP tasks such as cross-lingual retrieval, summarization, and dialogue systems

By bridging linguistic typology with geometric model diagnostics, this approach offers a principled pathway toward more equitable and effective multilingual AI.

Analogy

Machine Translation as Semantic Recombination (nDNA View)

What we study. How a model performs zero-shot translation by aligning two semantic genomes (source and target languages) inside its latent space. We read this process through the nDNA trio across depth: spectral curvature $\kappa_\ell$ (manifold bending), thermodynamic length $L_\ell$ (epistemic work), and a belief-field direction $\mathbf{v}_\ell$ (semantic steering). Our goal is to quantify a recombination load of meaning—how hard it is to splice corresponding concepts across languages without decoding.

Plain-language summary

Each language behaves like a genome of meaning. When two languages are syntenic (comparable order/structure), homologous loci align with little untwisting and the model pays a small energy bill. As typological distance grows (inversions, translocations, duplications), the latent chromosomes twist and cross; the model must spend more depth-wise “enzymatic work” to untangle and repair alignment—a larger recombination load.

Operator (what zero-shot MT does, abstractly)

Let $\mathcal{X}_s, \mathcal{X}_t$ be source/target corpora; at layer $\ell$ collect mean-centered hidden states

\[H_\ell^{(s)} \in \mathbb{R}^{n \times d}, \qquad H_\ell^{(t)} \in \mathbb{R}^{m \times d}.\]

Define an orthogonal alignment (Procrustes) $Q_\ell^\star = \arg\min_{Q \in O(d)} \lVert H_\ell^{(s)} Q - H_\ell^{(t)} \rVert_F$. The homology gap at depth $\ell$ is

\[D_\ell = \frac{1}{\sqrt{\min(n,m)}} \lVert H_\ell^{(s)} Q_\ell^\star - H_\ell^{(t)} \rVert_F,\]

or, equivalently, via principal angles ${\theta_i(H_\ell^{(s)}, H_\ell^{(t)})}_{i=1}^r$:

\[D_\ell^{\text{(PA)}} = \left(\sum_{i=1}^r \sin^2 \theta_i\right)^{1/2}.\]

Let $\mathbf{v}_\ell^{(s)}$ and $\mathbf{v}_\ell^{(t)}$ be unit belief directions (e.g., average normalized task gradient or steering vector) in the two spaces. A depth-local torsion cost (untwisting) is the misalignment of transported directions:

\[\tau_\ell = \arccos\left(\frac{\langle \mathbf{v}_\ell^{(s)}, Q_\ell^\star \mathbf{v}_\ell^{(t)} \rangle}{\lVert \mathbf{v}_\ell^{(s)} \rVert \lVert \mathbf{v}_\ell^{(t)} \rVert}\right),\]

or, if one tracks inter-layer transports, $\tau_\ell \approx \lVert \operatorname{skew}(\log(Q_{\ell+1}^\star Q_\ell^{\star \top})) \rVert_F$.

We read curvature from basis rotation across depth, e.g.

\[\kappa_\ell \propto \lVert \operatorname{sym}(\log(Q_{\ell+1}^\star Q_\ell^{\star \top})) \rVert_F,\]

and thermodynamic length as the cumulative epistemic step:

\[L_\ell = \lVert H_\ell^{(s)} - H_{\ell-1}^{(s)} \rVert_{F, W_\ell} \quad \text{(Fisher-/whitened norm)}, \qquad L_{\mathcal{I}} = \sum_{\ell \in \mathcal{I}} L_\ell.\]

The recombination load of meaning over a depth window $\mathcal{I}$ is

\[E_{\text{total}} = \sum_{\ell \in \mathcal{I}} \left(\underbrace{D_\ell}_{\text{homology gap}} + \lambda \underbrace{\tau_\ell}_{\text{untwisting}} + \mu \underbrace{\kappa_\ell}_{\text{curvature penalty}}\right),\]

optionally reweighted by $L_\ell$ to emphasize high-work regions.

Chromosome-level analogy (clear mapping)

Synteny (conserved order) $\leftrightarrow$ stable word order/constructions $\Rightarrow$ $D_\ell \downarrow$, $\tau_\ell \downarrow$.
Structural variants (inversions, translocations, duplications, deletions) $\leftrightarrow$ order flips, topic-comment, classifier systems, null elements $\Rightarrow$ $D_\ell \uparrow$, $\tau_\ell \uparrow$.
Recombinases/strand exchange $\leftrightarrow$ attention-mediated locus matching ($Q_\ell^\star$).
Topoisomerases $\leftrightarrow$ depth-wise untwisting (torsion $\tau_\ell$).
Mismatch repair $\leftrightarrow$ pruning implausible alignments via belief consistency.

Micro-mechanics (junctions, bias, asymmetry)

Ambiguity as Holliday junctions. Competing alignments form junctions in latent space; resolution appears as sharp drops in $D_\ell$ with spikes in $\kappa_\ell$ or $\tau_\ell$.

Gene conversion (directional overwrite). Dominant-language priors can overwrite rare target constructions $\Rightarrow$ asymmetric En→X vs. X→En difficulty mirrored in $\tau_\ell$ and $\mathbf{v}_\ell$ drift.

Polymerase slippage (repetitions). Local alignment loops around high-gain $n$-grams produce repetition; detectable as oscillatory turns of $\mathbf{v}_\ell$ with small $D_\ell$ but elevated $\kappa_\ell$.

Toolbox: Diagnostics and Controls (actionable)

D1. Homology gap estimator. Use orthogonal Procrustes or principal angles to compute $D_\ell$; report $D_{\mathcal{I}} = \sum_{\ell \in \mathcal{I}} D_\ell$ with bootstrap CIs.

D2. Torsion tracker. Estimate $\tau_\ell$ via transported belief directions or $\lVert \operatorname{skew} \log(Q_{\ell+1}^\star Q_\ell^{\star \top}) \rVert_F$; flag depth-slices where $\tau_\ell$ concentrates.

D3. Curvature profile. Track $\kappa_\ell$ to locate regions where alignment requires bending the manifold; penalize noisy, jagged profiles.

D4. Recombination load. Aggregate $E_{\text{total}}$ over $\mathcal{I}$; use it as a generation-free predictor of MT difficulty and a budget to compare models.

C1. Reduce $D_\ell$ (tighten homology). Shared subword/morphology adapters, lexicon priors, pronunciation/romanization bridges; encourage basis overlap to shrink $D_\ell$.

C2. Reduce $\tau_\ell$ (ease untwisting). Syntax-aware adapters and reordering curricula that introduce non-isomorphic orders gradually; minimize late-depth torsion.

C3. Stabilize $\kappa_\ell$ (preserve flexibility). Geometry-preserving distillation (match spectra/length) to avoid flattening curvature during compression.

C4. Seed hotspots (anchor exchange). Inject high-MI anchors (phrase tables, named entities) to create reliable strand-exchange sites that lower both $D_\ell$ and $\tau_\ell$.

Key takeaways

Distance $D_\ell$ measures how far homologous loci must slide; torsion $\tau_\ell$ measures how much untwisting is required; curvature $\kappa_\ell$ penalizes bending the manifold to make the splice.

The recombination load $E_{\text{total}}$ is a generation-free predictor of MT difficulty; low for syntenic pairs (e.g., En↔Fr/It/De), high for rearranged pairs (e.g., En↔Zh/Ja/Th).

Controls: shrink $D_\ell$ (homology adapters), shrink $\tau_\ell$ (reordering priors), and stabilize $\kappa_\ell$ (geometry-preserving KD). Use $E_{\text{total}}$ as the budget to trade speed/size vs. translation quality.

Machine Translation – Think of each language as a genome with its own chromosomal layout; zero-shot translation is like trying to perform homologous recombination between two genomes without ever expressing a phenotype. When the genomes (languages) are syntenic—gene order largely collinear—alignment is easy: low semantic displacement is like small edit distance, and low semantic torsion means little topological strain, so the “recombination machinery” needs little energy (low Total Epistemic Effort) to splice meaning across. As languages drift, you see structural variants—inversions, translocations, duplications—so manifolds twist and cross (torsion rises) and segments no longer match positionally (distance rises). Now the system must pay extra “enzymatic work,” akin to topoisomerases resolving supercoils and repair complexes bridging broken ends—your epistemic force across layers. Romance pairs (En↔Fr/It/De) behave like closely related species with conserved blocks: low torsion, short paths, high BLEU. Typologically distant pairs (En↔Zh/Ja/Th) resemble genomes with major rearrangements: high torsion, long paths, and weaker recombination yield—BLEU drops—even though no decoding occurs. In this view, GENOME-MT measures the recombination load of meaning: semantic distance = how far the loci are, torsion = how much topological untwisting is required, and the layerwise sum (thermodynamic length + torsion penalty) is the free-energy bill for crossing from one language’s semantic genome to the other.

References

[1] Papineni, Kishore, Roukos, Salim, and others “BLEU: a method for automatic evaluation of machine translation” ACL (2002).

[2] Dryer, Matthew S. and Haspelmath, Martin “The World Atlas of Language Structures Online” arXiv preprint (2013).

[3] Birch, Alexandra, Osborne, Miles, and others “Predicting success in machine translation from fluency and adequacy” ACL (2008).

[4] Mager, Manuel et al. “Typologically Diverse and Low-resource Languages in Multilingual NLP” Computational Linguistics (2021).

[5] Joshi, Aravind K “Centered embedding in human language” Cognition (1987).

[6] Comrie, Bernard “Language universals and linguistic typology” arXiv preprint (1989).

[7] Ohno, Susumu “Evolution by gene duplication” arXiv preprint (1970).

[8] Lewin, Benjamin “Genes VII” arXiv preprint (2000).

[9] Li, Charles N. and Thompson, Sandra A. “Topic and Comment in Chinese” arXiv preprint (1981).

[10] Combes, Patrick et al. “Understanding Cross-lingual Alignment in Multilingual Models” TACL (2023).

[11] King, Mary-Claire and Wilson, Allan C “Evolution at two levels in humans and chimpanzees” Science (1975).

[12] Littell, Patrick et al. “URIEL and lang2vec: Representing languages as typological, geographical, and phylogenetic vectors” EACL (2017).

[13] Malaviya, Chaitanya et al. “Learning language representations for typology prediction” EMNLP (2017).

Language Pair	English → Target				Target → English				Linguistic Commentary
	Dist	Torsion	\(\mathcal{E}_{\text{total}}\)	BLEU	Dist	Torsion	\(\mathcal{E}_{\text{total}}\)	BLEU
French	0.18	0.06	0.19	41.8	0.15	0.04	0.16	43.5	Minimal reordering, analytic structure.
German	0.22	0.08	0.24	38.6	0.20	0.07	0.22	39.7	Case-marking + verb-second placement.
Italian	0.20	0.07	0.21	40.1	0.18	0.06	0.20	41.3	Shared SVO structure, low torsion.
Hindi	0.44	0.27	0.56	26.1	0.39	0.21	0.46	28.4	SOV order, script and morphological divergence.
Bengali	0.48	0.31	0.63	24.8	0.42	0.26	0.54	26.7	Compound verbs, lexicosyntactic shifts.
Tamil	0.50	0.35	0.68	23.2	0.43	0.29	0.59	25.6	Agglutinative Dravidian structure; distant typology.
Chinese	0.71	0.58	1.12	16.4	0.61	0.44	0.88	18.9	Tonal and aspectual systems; no case markers.
Thai	0.67	0.49	1.00	18.2	0.59	0.38	0.84	20.5	Classifier system, tone mismatch, SVO similarity.
Japanese	0.81	0.72	1.39	13.5	0.69	0.55	1.08	16.2	Topic-prominence, scrambling, honorific complexity.

nDNA - the Semantic Helix of Artificial Cognition