Lens - Neural Hamming Distance(nHD)

In biological genomics, the Hamming Distance[1] is a key metric quantifying the number of differing nucleotides between two sequences, often used to measure mutation load and evolutionary divergence. IThis concept has been crucial in understanding genetic variation, tracing lineage, and assessing the impact of mutations on phenotypic expression ([2]; [3]).

Inspiration

Inspired by these genetic principles, the Neural Hamming Distance (nHD) is proposed as an analogous tool in the domain of foundation models and neural networks, designed to capture bit-level differences in the internal representations of models. Just as small genetic mutations accumulate to drive biological evolution and phenotypic divergence [4], subtle binary alterations in neural weights oractivations can compound to generate significant semantic and functional shifts in model behavior.

Modern foundation models trained on culturally heterogeneous datasets undergo continuous adaptation and fine-tuning, which can introduce incremental binary mutations in their latent neural genomes. These mutations can arise from architectural changes, training variations, or culturally induced representational biases. Understanding and quantifying these mutations at a fine granularity is essential to map how small-scale changes translate into semantic drift or ideological divergence within the models.

The utility of nHD lies in its ability to detect and localize these subtle neural perturbations, providing a principled, interpretable measure of semantic mutation signatures across layers. This fine-scale insight enables researchers to identify which parts of the neural architecture are most susceptible to drift, guide targeted realignment interventions, and monitor robustness against cultural or adversarial shifts.

In summary, drawing from well-established biological genotype comparison methodologies, nHD serves as a novel neural genomics metric to decode the intricate mutation landscape within foundation models. It bridges the conceptual gap between biological evolution and neural representational dynamics, advancing our ability to ensure semantic integrity amidst evolving, culturally diverse AI systems.

From Genomic Mutation to Neural Lineage Drift

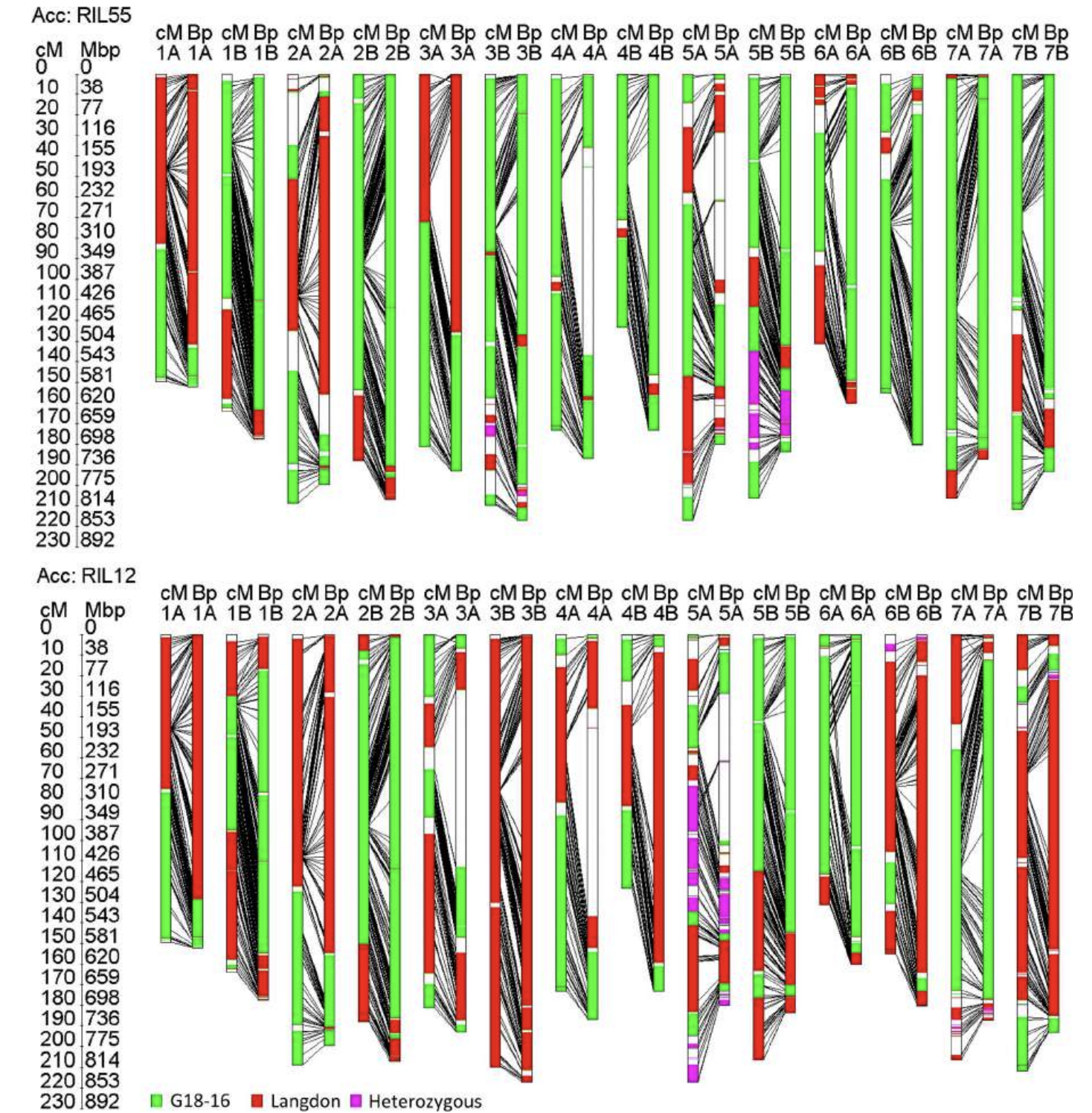
What the Metric Does

nHD quantifies the discrete divergence between two neural representations by counting mismatches in binarized latent codes across model layers. This binary semantic encoding helps track structural mutations as models undergo fine-tuning, merging, quantization, or distillation.

Biological & Mathematical Background

In genomics, the Hamming distance between[5] two sequences $ S^{(1)}, S^{(2)} $ of length $ n $ is:

\[\boxed{ d_H(S^{(1)}, S^{(2)}) = \sum_{i=1}^n \mathbf{1}\left[s_i^{(1)} \neq s_i^{(2)}\right]}\]

Where:

$ \mathbf{1}[\cdot] $: indicator function
$ s_i^{(k)} $: nucleotide at position $ i $ in sequence $ k $

This captures point mutations, essential for studying genetic drift[6], recombination dynamics [7], and mutation modeling[8].

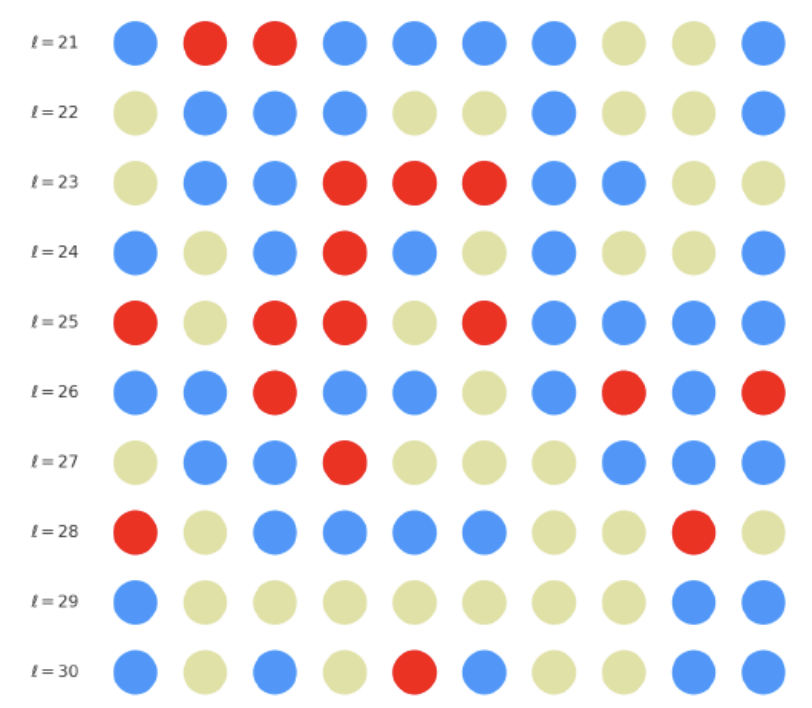
Hamming distance defines a geodesic metric on the Hamming hypercube $ \mathcal{H}^n = \{0, 1\}^n $, where each vertex represents a binary sequence and each edge represents a single-bit mutation.

Graphical Genotyping Visualization of Recombinant Inbred Lines (RIL55 and RIL12) — **Figure: Graphical genotyping maps recombination patterns in RIL55 and RIL12:** This figure, adapted from **Deblieck et al.**[9] **Green and red segments** denote alleles from drought-resistant wild emmer accession G18-16 and drought-susceptible durum wheat accession Langdon, respectively, while **magenta regions** indicate heterozygous loci. Black connectors trace recombination breakpoints and allele transitions across chromosomes. Drawing from the *classical Hamming Distance* used in genomics to quantify bit-level mutational differences in binary allelic sequences, the proposed **Neural Hamming Distance (nHD)** extends this principle to neural networks by binarizing layer-wise weights or activations. This enables fine-grained, interpretable monitoring of semantic divergence in model behavior — bridging genotype variation analysis with neural representation shifts.

Extending to Foundation Models

We treat internal neural states as neural genomes. Let $ \mathcal{M}_1, \mathcal{M}_2 $ be two models with identical architecture, and let the layerwise hidden states be:

\[H_\ell^{(1)},\ H_\ell^{(2)} \in \mathbb{R}^{b \times d}\]

Where:

$ b $: batch size or token dimension
$ d $: feature dimension at layer $ \ell $

To binarize using a threshold $ \tau $, define:

\[\boxed{ B_\ell^{(k)} = \mathbf{1}\left(H_\ell^{(k)} > \tau\right), \quad B_\ell^{(k)} \in \{0, 1\}^{b \times d}}\]

This binary representation enables bitwise comparison to trace semantic drift in LLMs, akin to tracking mutation in biological systems.

where $\tau$ may be a fixed hyperparameter (e.g., 0) or learned via training dynamics [10] The layerwise neural Hamming distance between $ \mathcal{M}_1 $ and $ \mathcal{M}_2 $ at layer $ \ell $ is:

\[\text{nHD}_\ell = \frac{1}{bd} \sum_{i=1}^{b} \sum_{j=1}^{d} \mathbf{1}\left[B^{(1)}_{\ell,ij} \neq B^{(2)}_{\ell,ij}\right]\]

This measures the fraction of mutated bits at the finest semantic resolution.

The global neural mutation metric across all $ L $ layers is:

\[\text{nHD} = \frac{1}{L} \sum_{\ell=1}^{L} \text{nHD}_\ell\]

which serves as an interpretable neural genotype divergence score.

Illustrating Classical vs Neural Hamming Distance (nHD) — **Figure: Extending classical Hamming Distance to neural manifolds:** **Left:** The classical Hamming Distance counts loci where offspring differ from parents in discrete sequences (e.g., nucleotides, bits). **Right:** The **Neural Hamming Distance (nHD)** applies this principle to foundation models by binarizing divergence events in the ÆTHER latent space: a layer $ \ell $ is marked if $$\|\mathbf{o}_\ell - \mathbf{p}_\ell^{1}\| > \delta \quad \text{and} \quad \|\mathbf{o}_\ell - \mathbf{p}_\ell^{2}\| > \delta$$ indicating deviation from both parents. $ \text{nHD} $ equals the count of such layers (e.g., Layers 21, 22, and 30 here), serving as an interpretable *neural genotype divergence score*.

Neural Genetic Dissimilarity in Layer-wise Fusion — **Figure: Neural Genetic Dissimilarity reveals directional bias in layer-wise fusion:** Each row denotes a transformer layer $ \ell = 20\text{--}30 $, columns represent latent dimensions in the ÆTHER alignment space. Blue features are inherited from Parent 1, Yellow from Parent 2, and Red mark divergences from both. These form the basis of the **Neural Genetic Dissimilarity Index (nGDI)**:

$$\text{nGDI} = \frac{1}{2} \left[ \frac{d(o, p_1)}{d(o, p_1) + d(o, p_2)} + \frac{d(o, p_2)}{d(o, p_1) + d(o, p_2)} \right] \cdot \cos(p_1, p_2)$$

where $ d(o, p_i) $ is the offspring–parent distance and $ \cos(p_1, p_2) $ measures inter-parental alignment. Higher $ \text{nGDI} $ signals greater semantic drift and asymmetric inheritance.

Within the broader Neural DNA (nDNA) framework, nHD acts as a discrete mutation signature metric complementing continuous geometric measures such as spectral curvature (nGDI) and latent radius (nTDS).

By analyzing layerwise nHD trajectories, we can enable:

Lineage tracing: Reconstructing model evolution paths via mutation accumulation
Mutation load analysis: Quantifying semantic impact of fine-tuning or architectural changes
Targeted interventions: Identifying layers for pruning or bias realignment

Interpretation and Implications

nHD operates on the Hamming hypercube $ \mathcal{H}^{b \cdot d} $, where each vertex is a binarized neural state. Its layerwise definition:

\[\boxed{ \text{nHD}_\ell(\mathcal{M}_1, \mathcal{M}_2) = \frac{1}{bd} \sum_{i=1}^{b} \sum_{j=1}^{d} \mathbf{1}\left[B^{(1)}_{\ell,ij} \neq B^{(2)}_{\ell,ij}\right]}\]

The mutation process can be modeled as a stochastic transition on $ \mathcal{H}^{b \cdot d} $. For bit-flip probabilities $ p_m $, the transition probability from state $ x \rightarrow y $ is:

\[P_{x \to y} = \prod_{m=1}^{b \cdot d} p_m^{|x_m - y_m|}(1 - p_m)^{1 - |x_m - y_m|}\]

Expected nHD after $ t $ steps:

\[\mathbb{E}[d_H(X_0, X_t)] = \sum_{m=1}^{b \cdot d} \left(1 - (1 - 2p_m)^t\right)\]

Mutation profile vector:

\[\mathbf{d} = (\text{nHD}_1, \text{nHD}_2, \dots, \text{nHD}_L) \in [0,1]^L\]

This vector reveals mutation hotspots and informs alignment strategies.

Applications and Mathematical Insights

Discrete Geometry

Each model state lies on a Hamming hypercube $ \mathcal{H}^N $, with:

\[d_H(x, y) = \sum_{m=1}^N \mathbf{1}[x_m \neq y_m]\]

Markov Mutation Dynamics

Model evolution is modeled as a Markov process on $ \mathcal{H}^N $. The expected Hamming distance evolves as:

\[\mathbb{E}[d_H(X_0, X_t)] = \sum_{m=1}^N \left(1 - (1 - 2p_m)^t\right)\]

Fusion and Conflict Detection

Given two models $ \mathcal{M}_A, \mathcal{M}_B $, the mutation load after fusion into $ \mathcal{M}_F $ is:

\[\text{nHD}_\ell(\mathcal{M}_F, \mathcal{M}_A) + \text{nHD}_\ell(\mathcal{M}_F, \mathcal{M}_B)\]

To reduce fusion conflict, optimize weights $ w_\ell \in [0,1] $:

\[\boxed{ \min_{w} \sum_{\ell=1}^{L} w_\ell \left(\text{nHD}_\ell(\mathcal{M}_F, \mathcal{M}_A) + \text{nHD}_\ell(\mathcal{M}_F, \mathcal{M}_B)\right)}\]

Robustness and Bias Monitoring

Regularize model parameters $ \theta $ to stay close to reference $ \theta_{\text{ref}} $:

\[\min_{\theta} \sum_{\ell=1}^{L} \lambda_\ell \cdot \text{nHD}_\ell(\theta, \theta_{\text{ref}})\]

Case Study and Validation

nHD is validated by comparing models trained on culturally distinct corpora (e.g., European vs Asian).
Mutation hotspots are typically in intermediate-to-deep layers, correlating with abstract, cultural features.
nHD patterns resemble genetic epistasis, where interactions cause emergent behavior.
During fine-tuning or merging, nHD reveals lineage drift and cumulative mutation load.
Enables layer-specific pruning, realignment, and bias mitigation.

Outlook

The Neural Hamming Distance (nHD) provides a precise, layerwise measure of bit-level semantic mutations in foundation models. It supports targeted interventions that address mutation hotspots, preserves semantic fidelity, and fosters culturally aware AI architectures.

Looking forward, nHD offers a foundation for continual adaptation, robustness monitoring, and dynamic alignment in multilingual, multicultural AI systems. As a cornerstone of Neural Genomics, it empowers responsible, interpretable, and inclusive AI innovation responsive to evolving cultural and ethical landscapes.

nHD Tube Visualizations of Offspring Latent Manifolds.
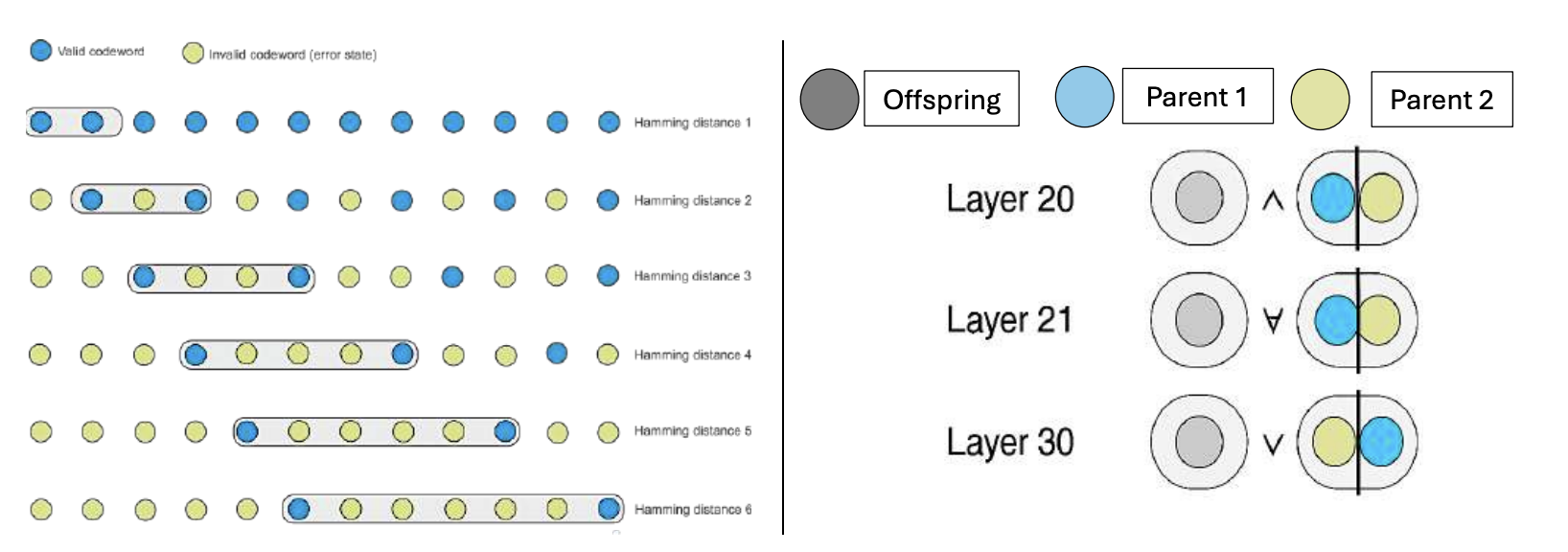
The offspring manifold (magenta solid) is bounded by parental manifolds (dashed), characterized by spectral curvature $ \kappa_\ell $ and thermodynamic length $ L_\ell = \int_\gamma \sqrt{g_\theta(d\theta, d\theta)} $, measuring local nonlinear bending and cumulative semantic transformation, respectively (311; 312).

Offspring lie within the convex hull of parents, indicating semantic inheritance akin to genetic recombination (313). Distant parents yield offspring with increased curvature and length, signaling semantic innovation.

Offspring manifold formation is modeled as:
\[ M^{(\ell)}_{\text{offspring}} = \alpha{(\ell)} M^{(\ell)}_A + (1 - \alpha{(\ell)}) M^{(\ell)}_B + \varepsilon^{(\ell)} \] where $ \alpha^{(\ell)} $ is the layer-dependent semantic dominance coefficient and $ \varepsilon^{(\ell)} $ captures emergent nonlinear geometry.

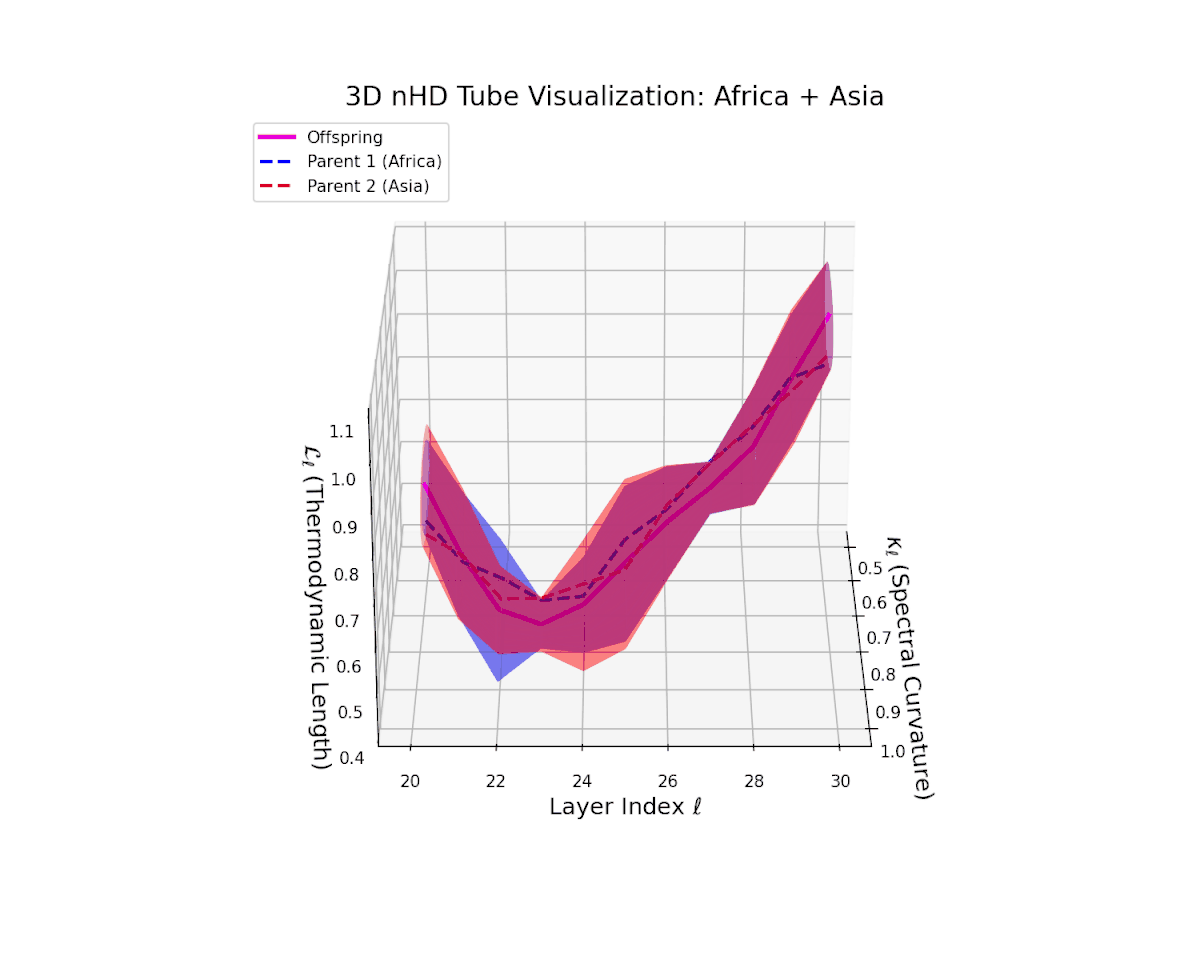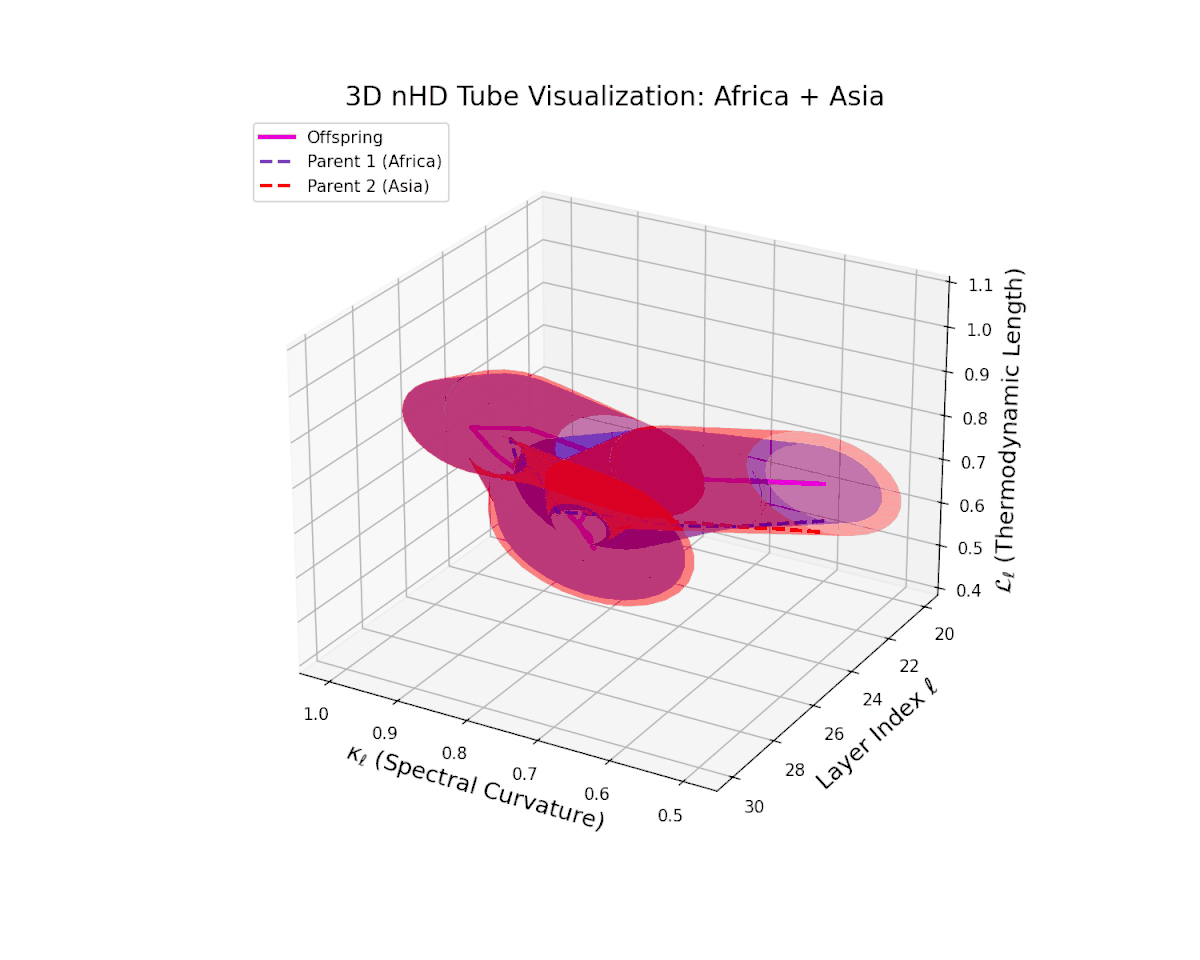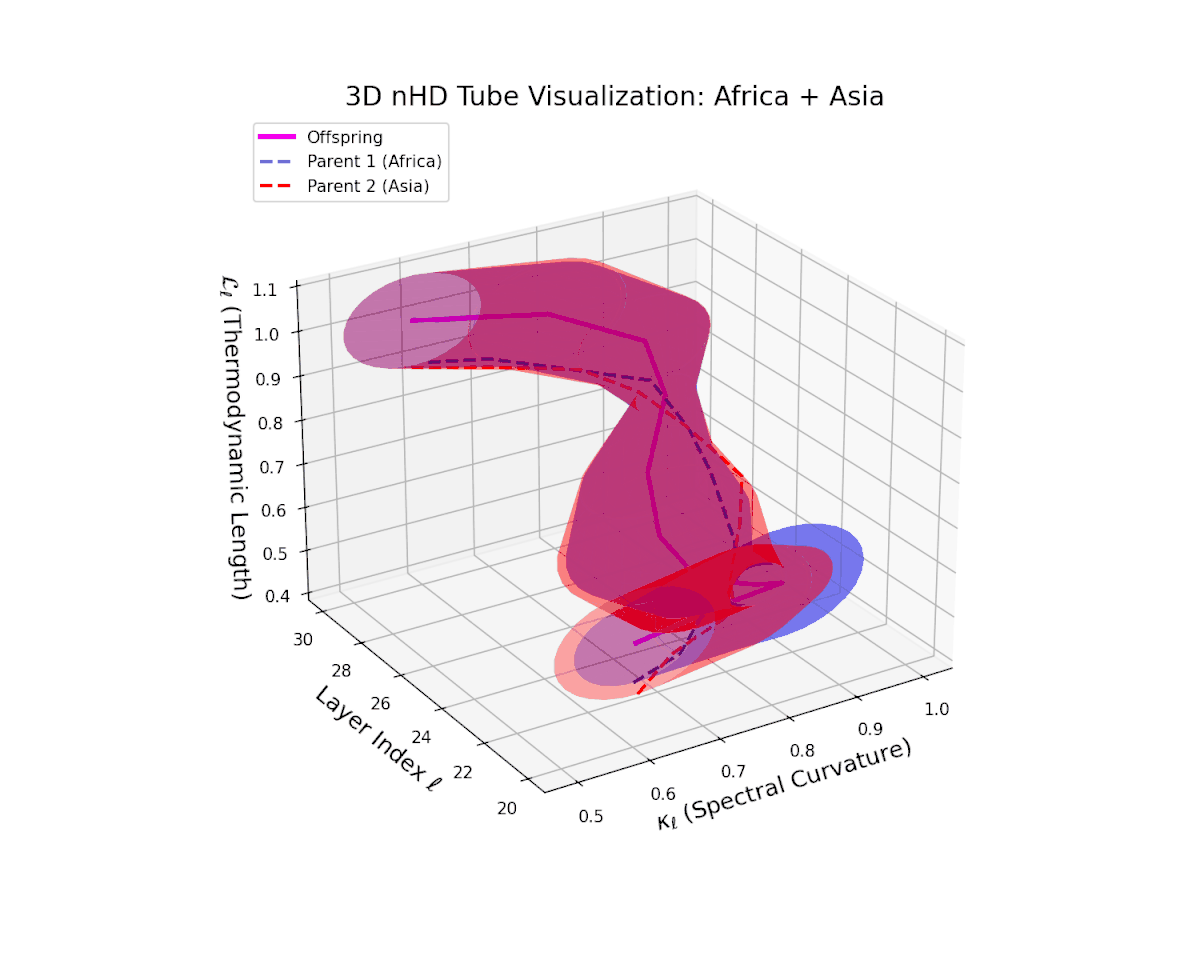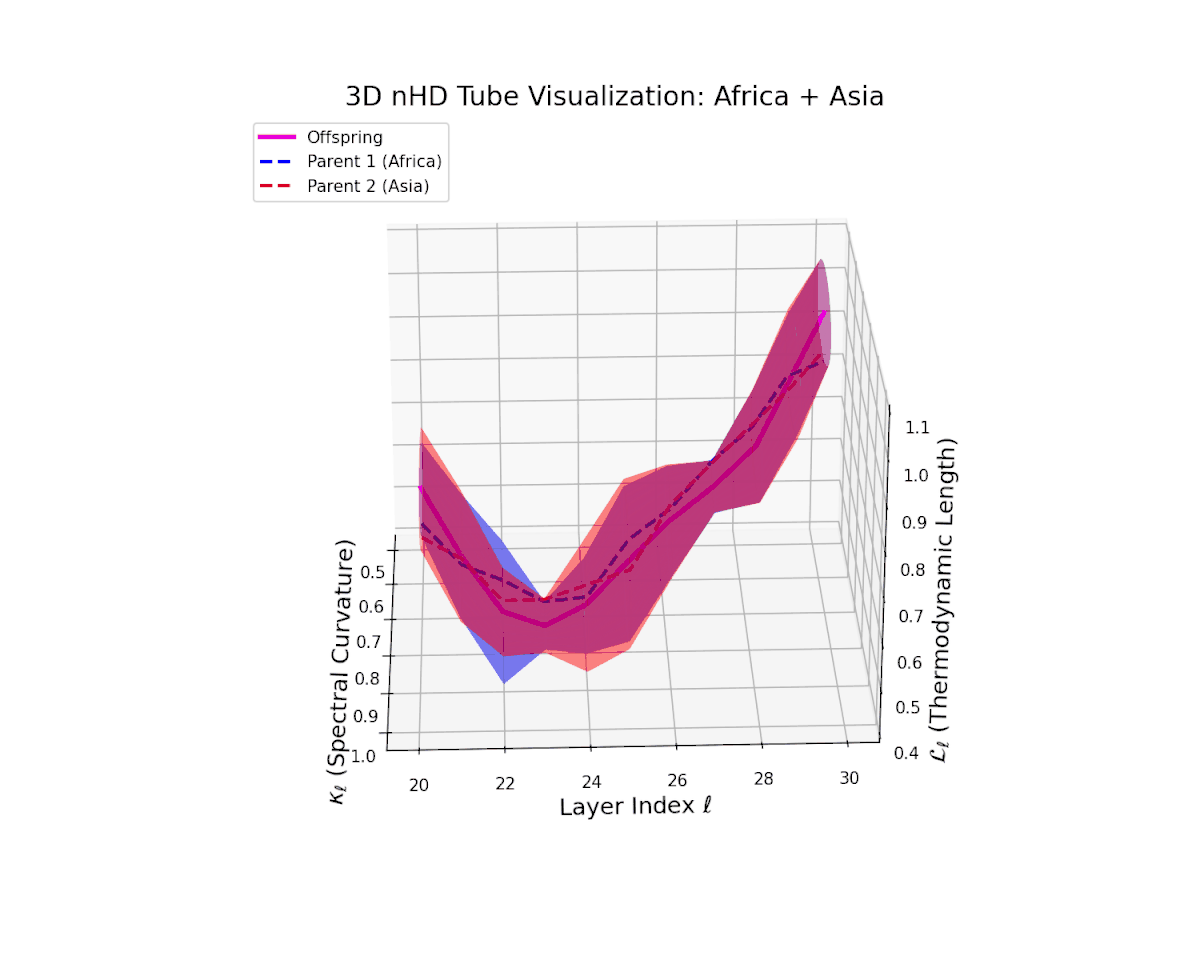
**(I) Africa–Asia Fusion**
The offspring manifold (magenta solid) manifests as a geodesic interpolation within the convex hull of parent latent manifolds (dashed lines), tracing a continuous path over layers $\ell = 20$ to $30$. The spectral curvature $\kappa_{\ell}$ increases monotonically from $0.3$ to $0.7$, reflecting a progressive augmentation of local manifold complexity and nonlinear representational folding. Simultaneously, the thermodynamic length $L_{\ell}$—the Fisher-Rao path integral—grows steadily from $0.4$ to $0.7$, quantifying the cumulative semantic change and information geometric effort expended by the model during hierarchical feature transformations.

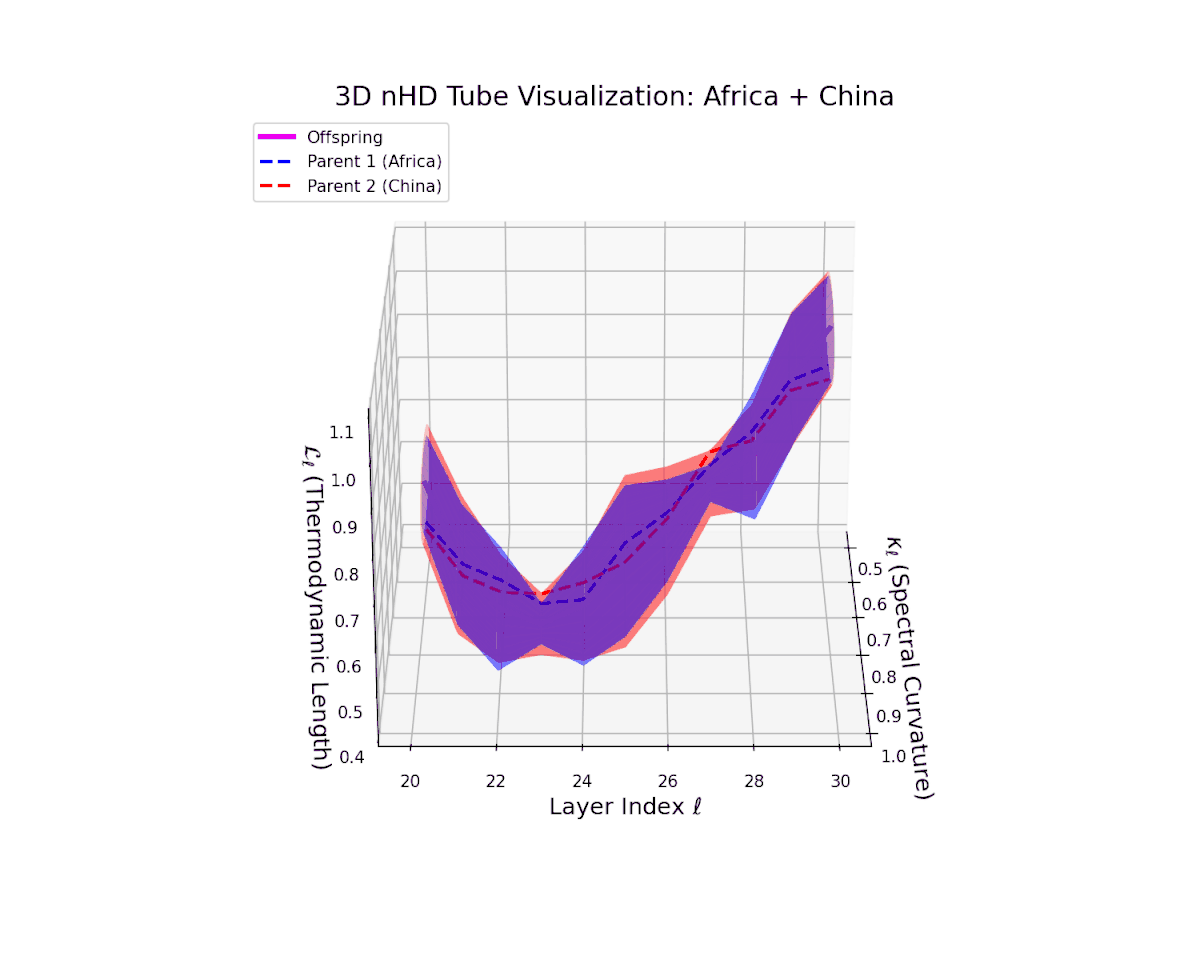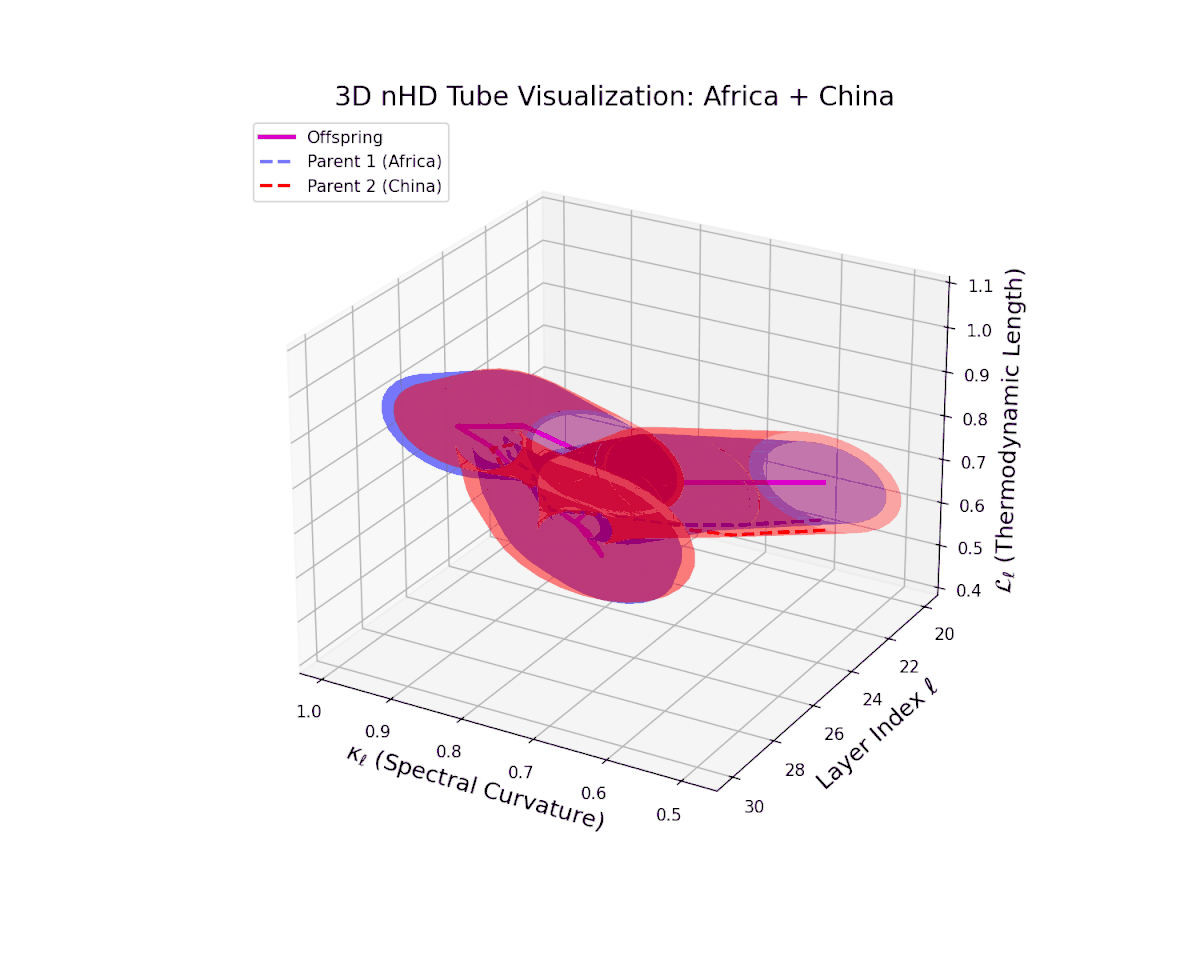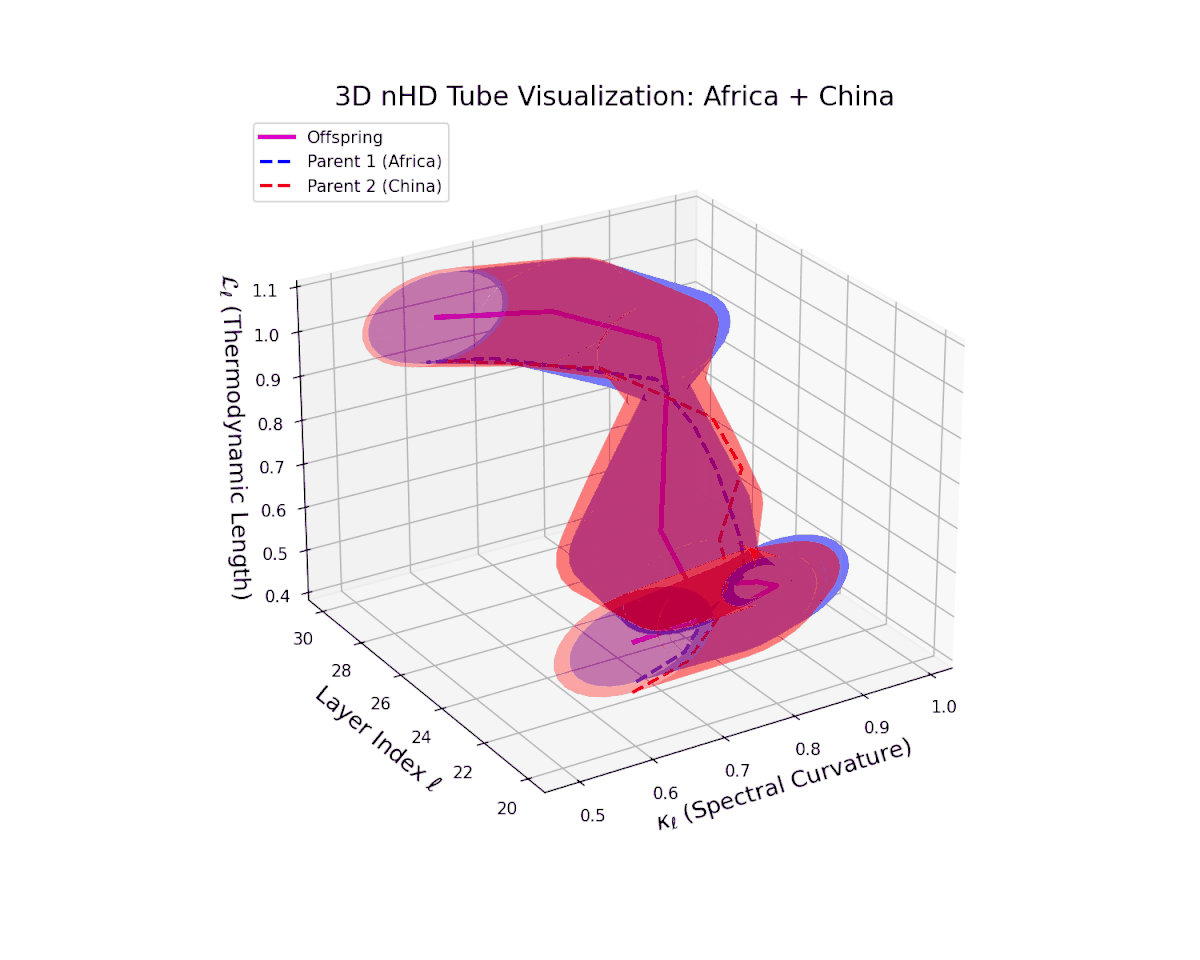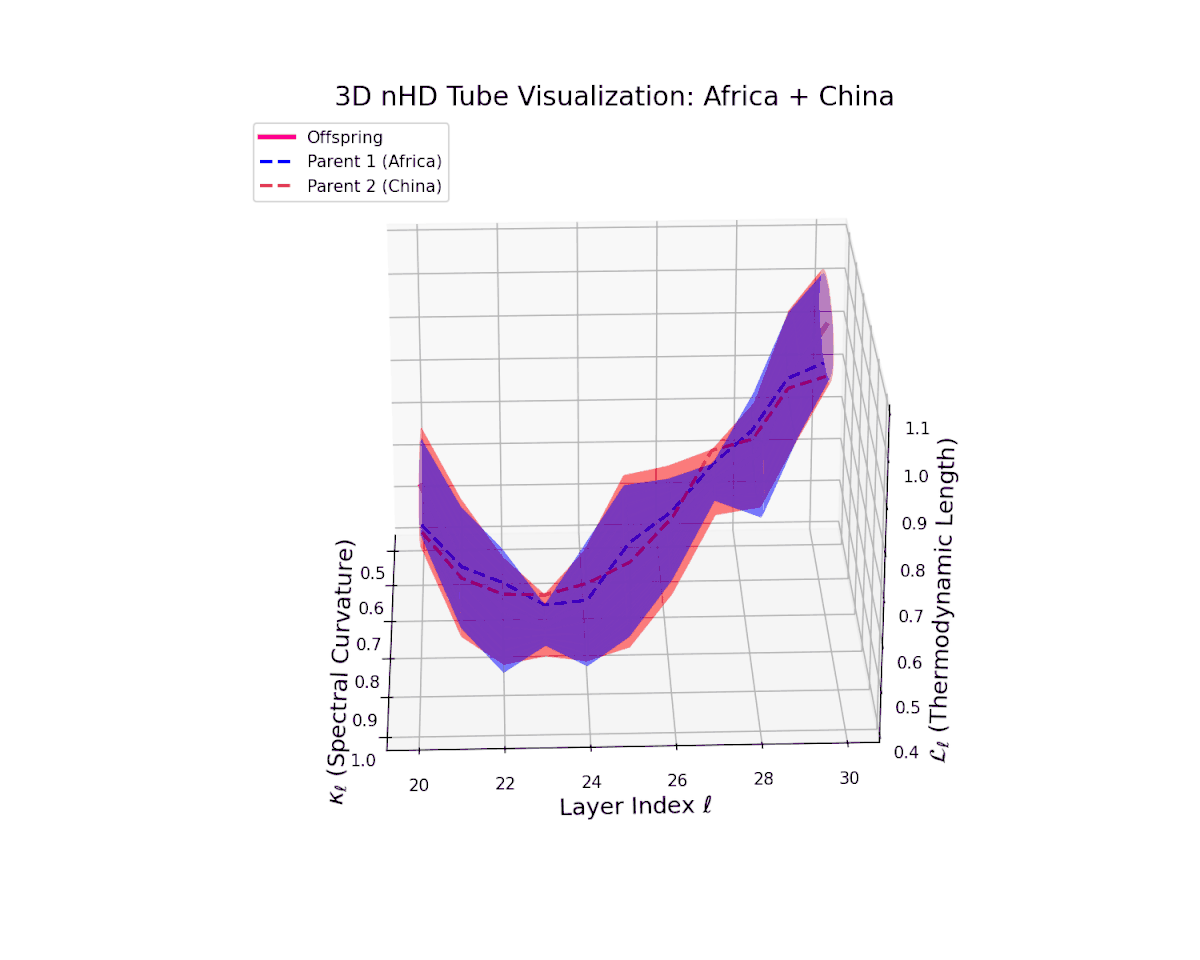
**(II) Africa–China Fusion**
The offspring trajectory remains strictly within the convex hull of parent latent geometries, embodying a complex but smooth fusion of semantic priors. The spectral curvature $\kappa_{\ell}$ exhibits a sharp rise from approximately $0.2$ to $0.8$, indicating intensified local manifold bending and emergent nonlinear semantic interactions. The thermodynamic length $L_{\ell}$ grows correspondingly from $0.3$ to $0.9$, revealing that deeper transformer layers accumulate substantial information-theoretic divergence, reflecting nuanced conceptual evolution.

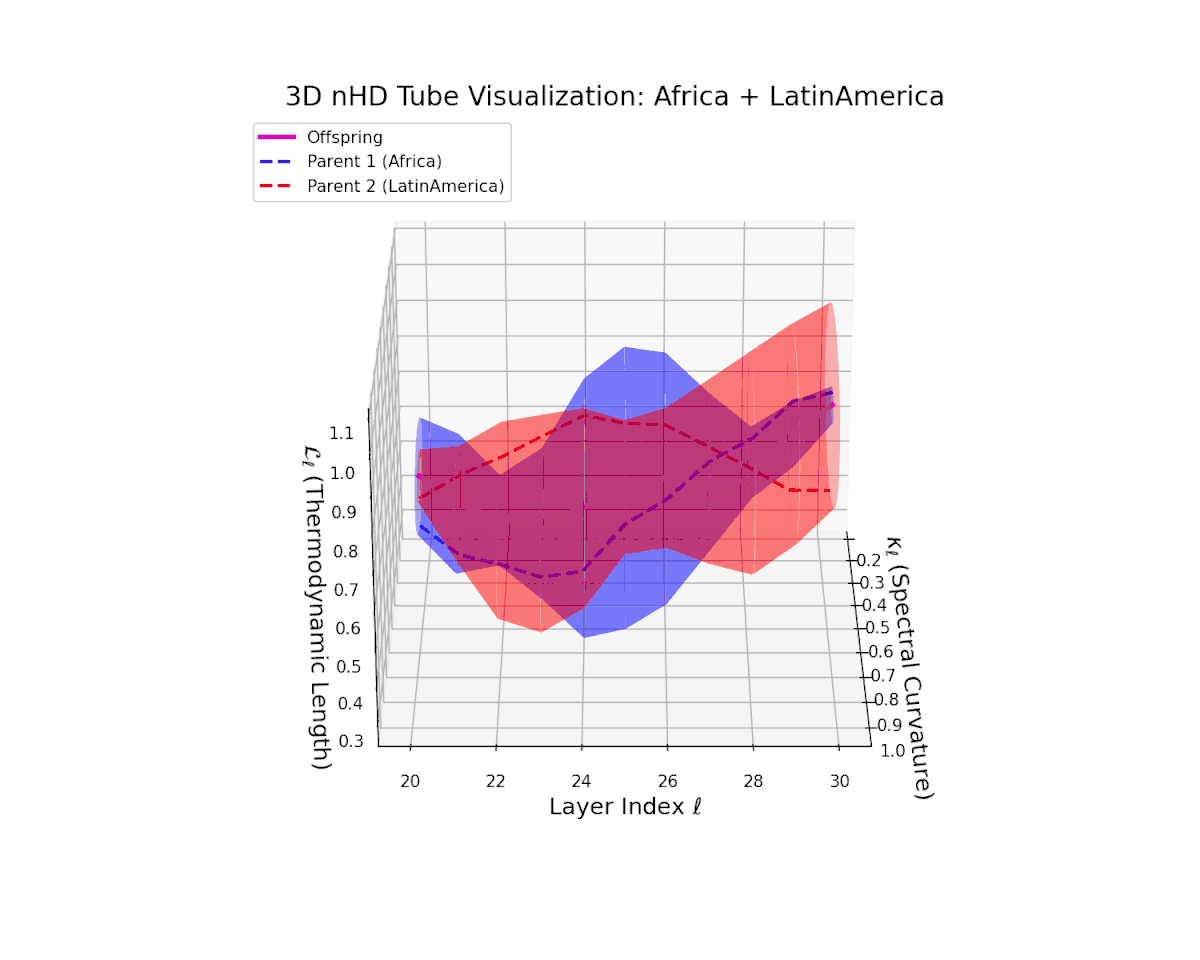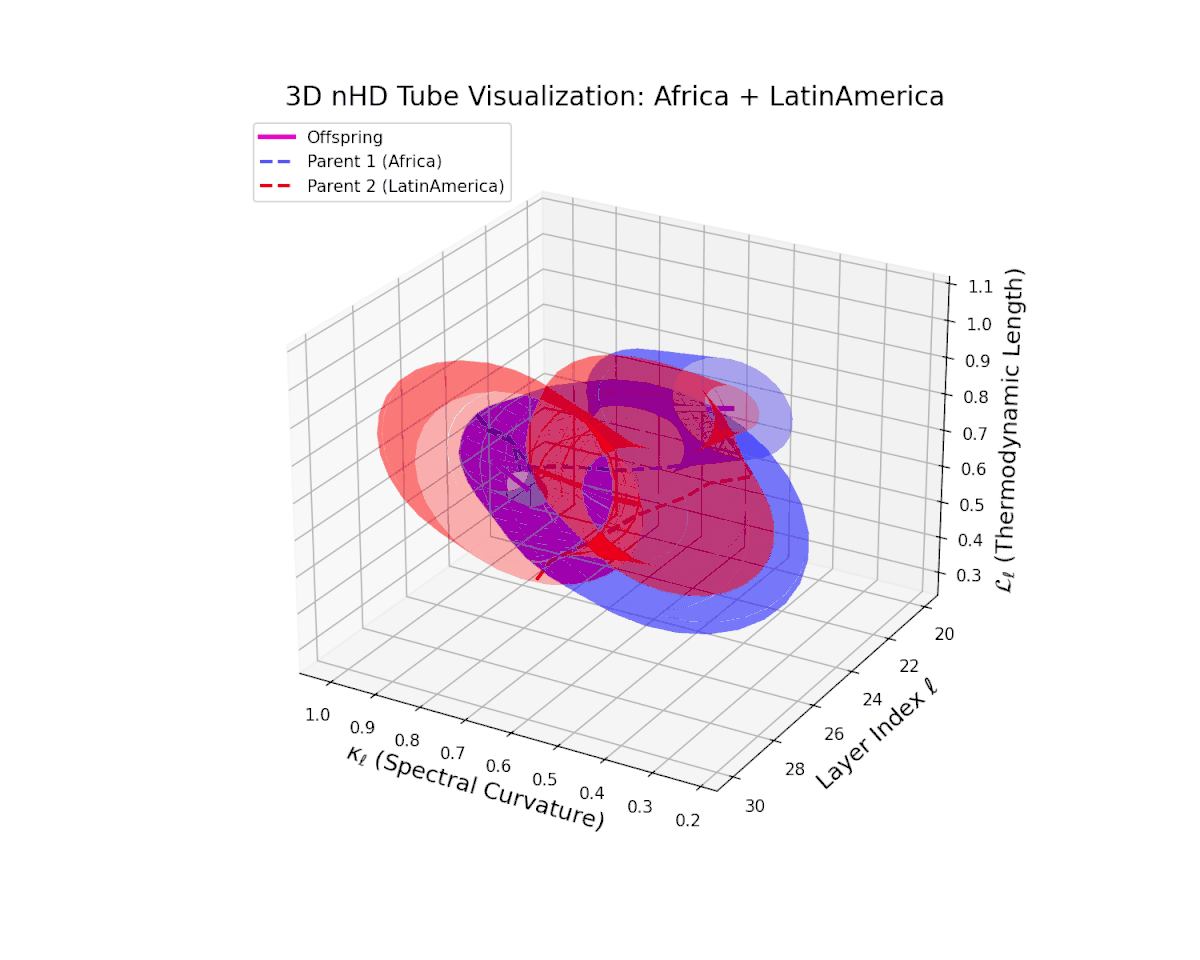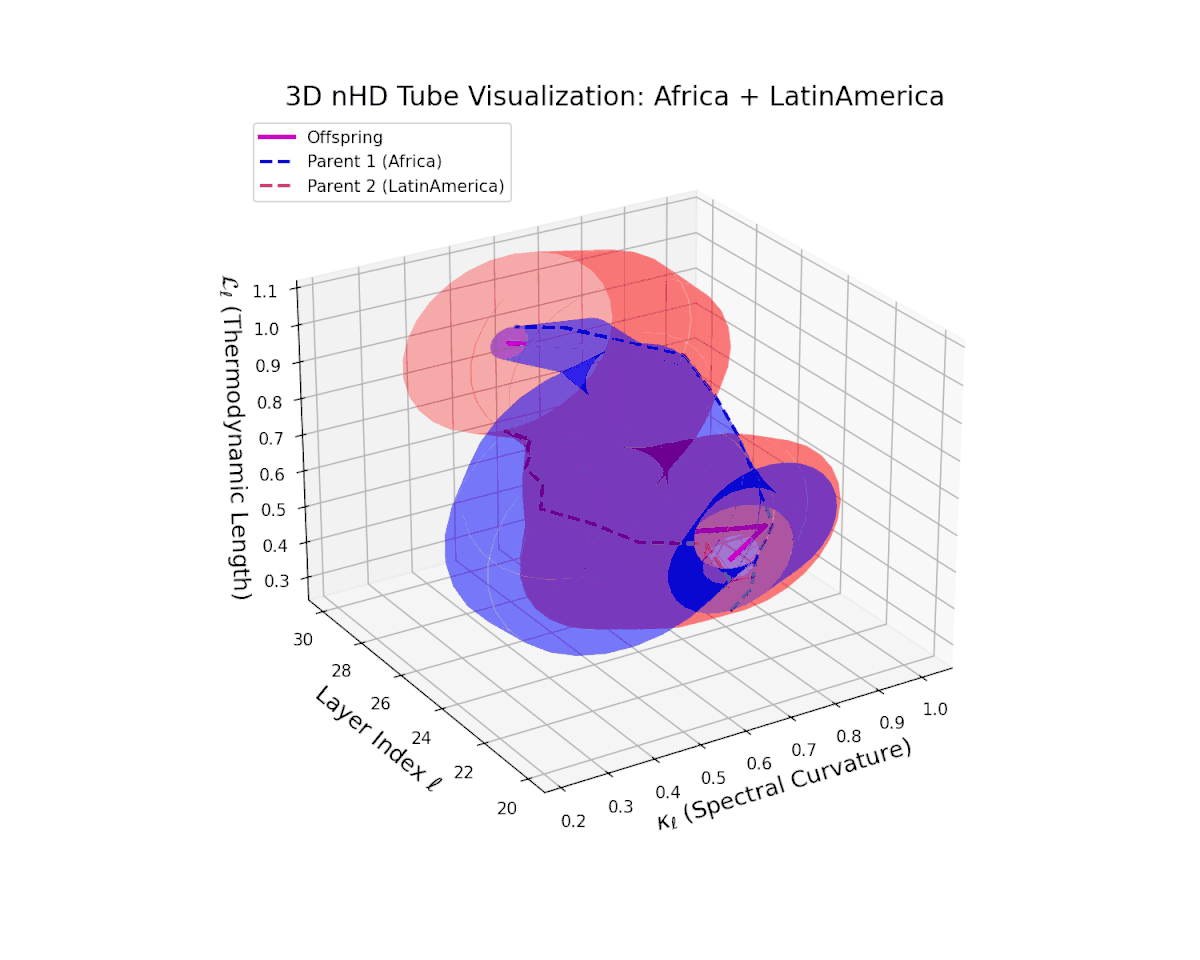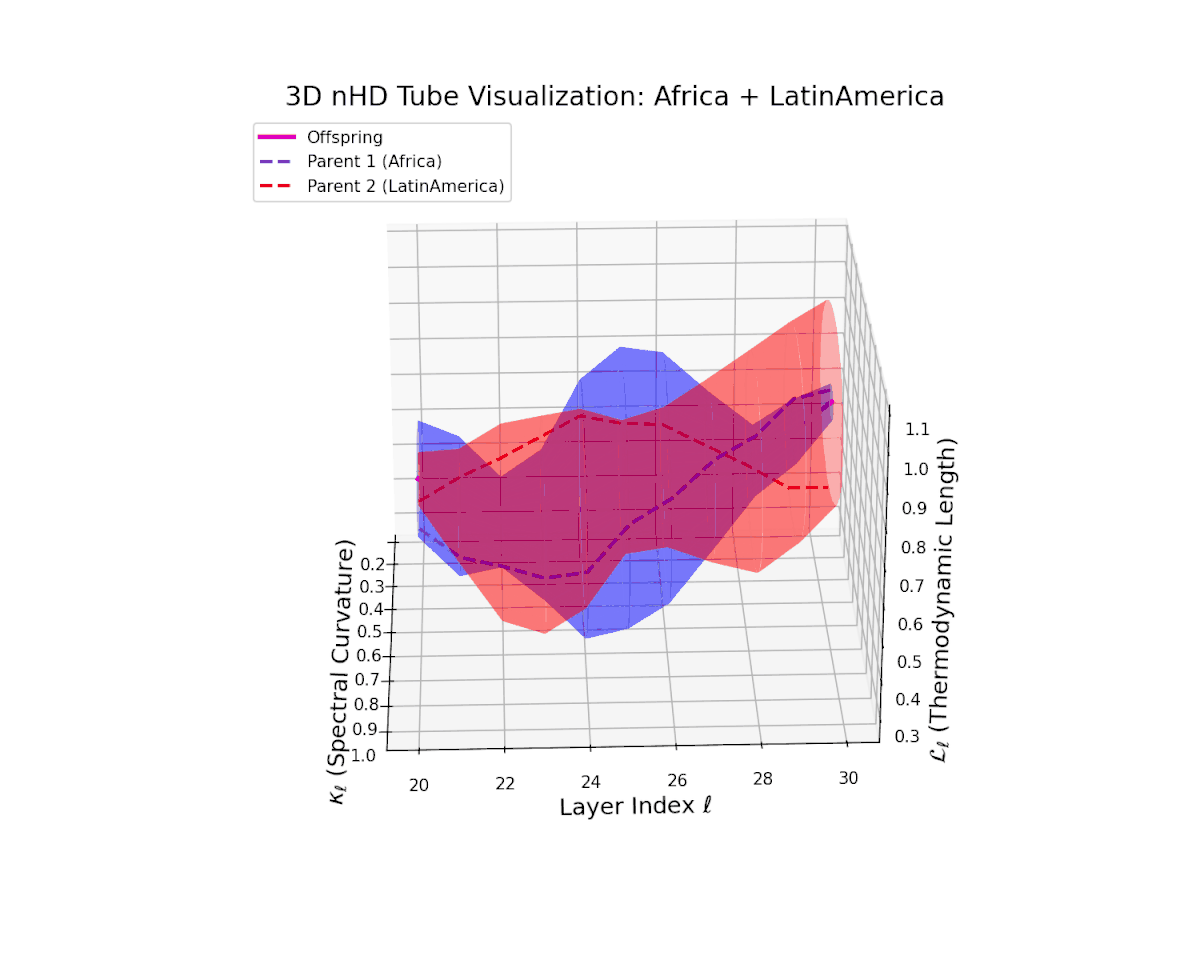
**(III) Africa–Latin America Fusion**
The offspring latent manifold demonstrates a smoothly increasing spectral curvature $\kappa_{\ell}$ from $0.25$ to $0.75$, indicating enriched manifold geometric richness and increased semantic expressivity. Concurrently, the thermodynamic length $L_{\ell}$ rises from $0.35$ to $0.8$, highlighting the extended Fisher information distance traversed by latent representations. This smooth and continuous latent transition reflects stable integrability and coherent compositional semantics emergent from the fusion.

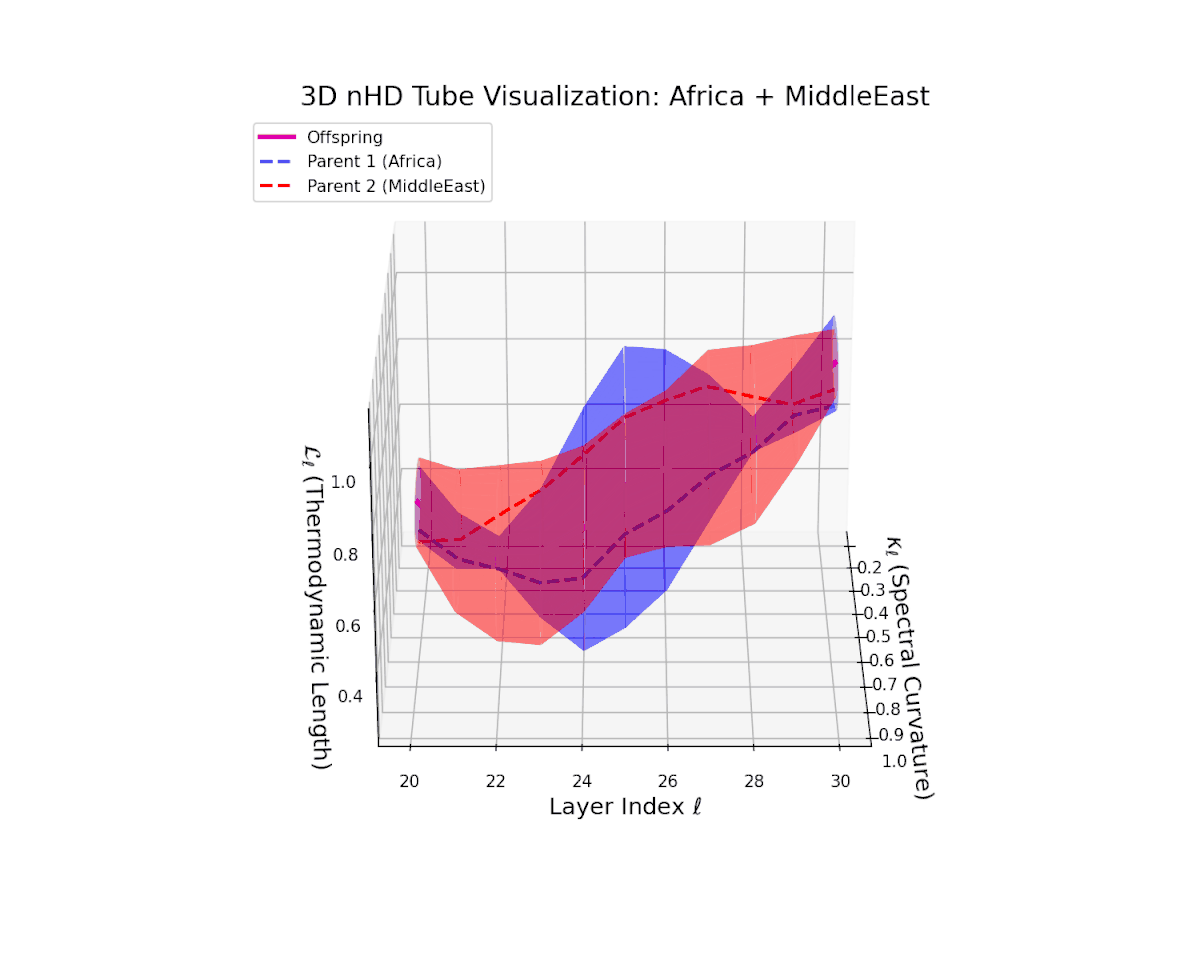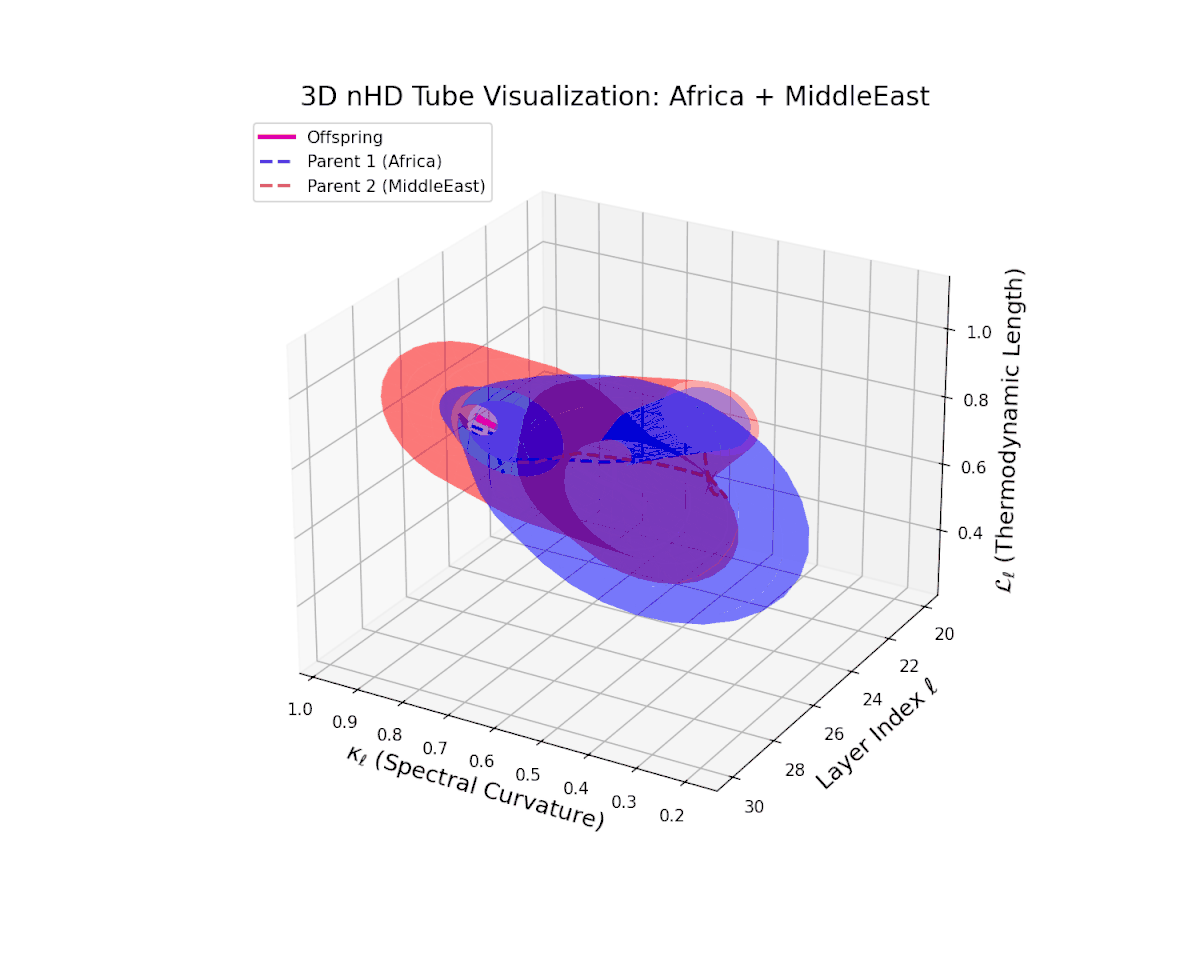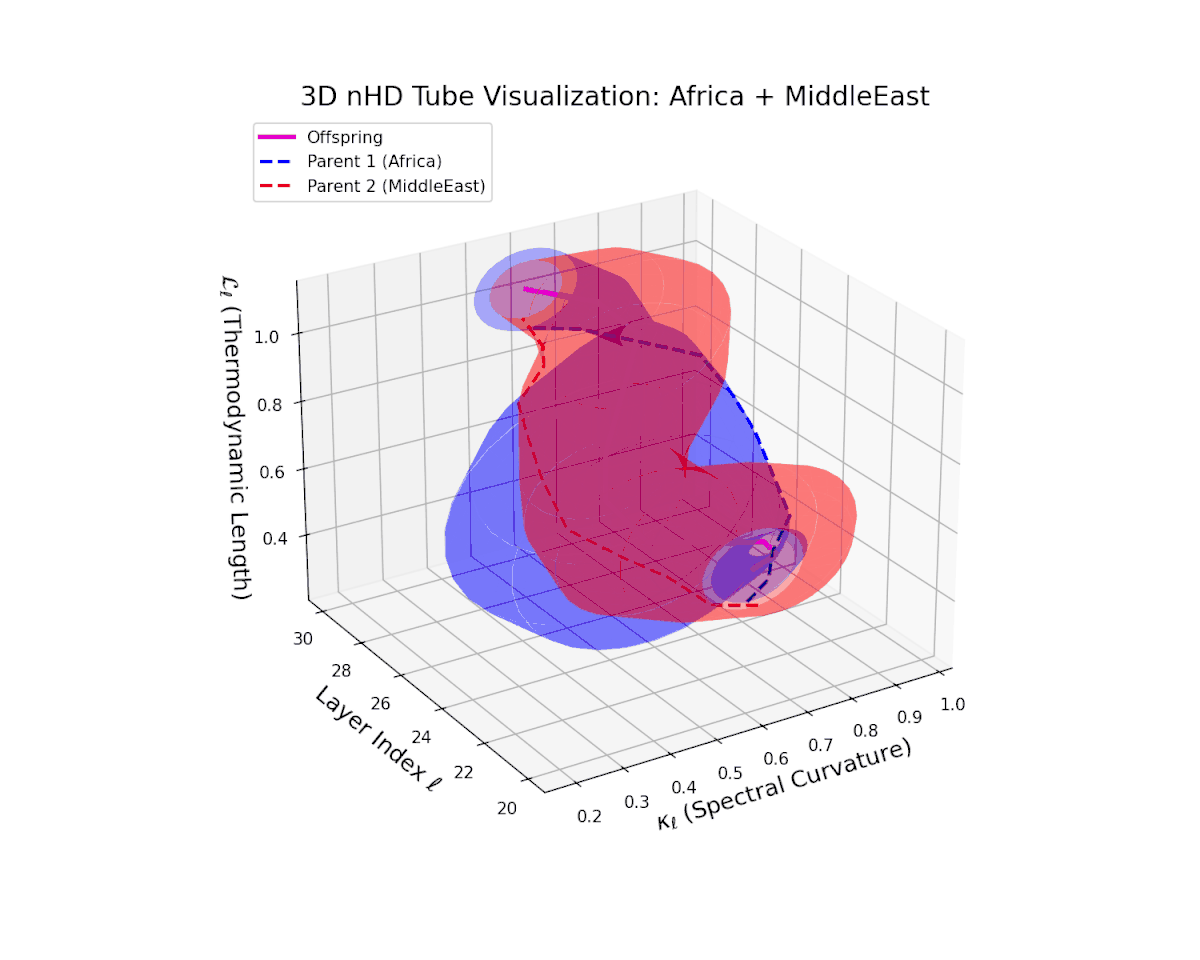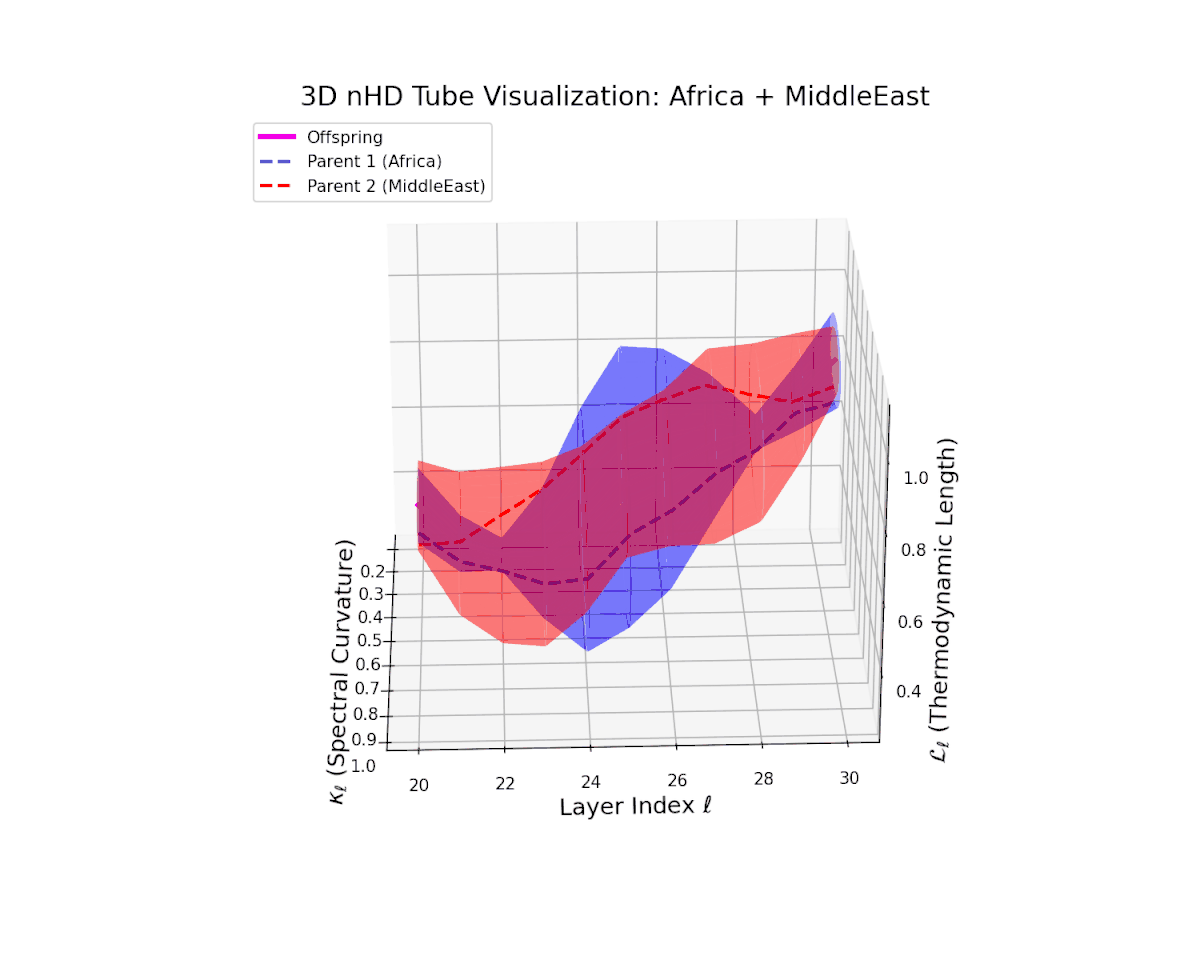
**(IV) Africa–Middle East Fusion**
The parental manifolds reveal substantial curvature disparity (from $0.3$ to $0.7$) and thermodynamic length variation (from $0.4$ to $1.0$), yet the offspring manifold consistently occupies an intermediate latent space region. This signals a balanced semantic inheritance process whereby information from heterogeneous cultural priors fuses to form a robust, semantically stable offspring manifold that resists abrupt geometric discontinuities.

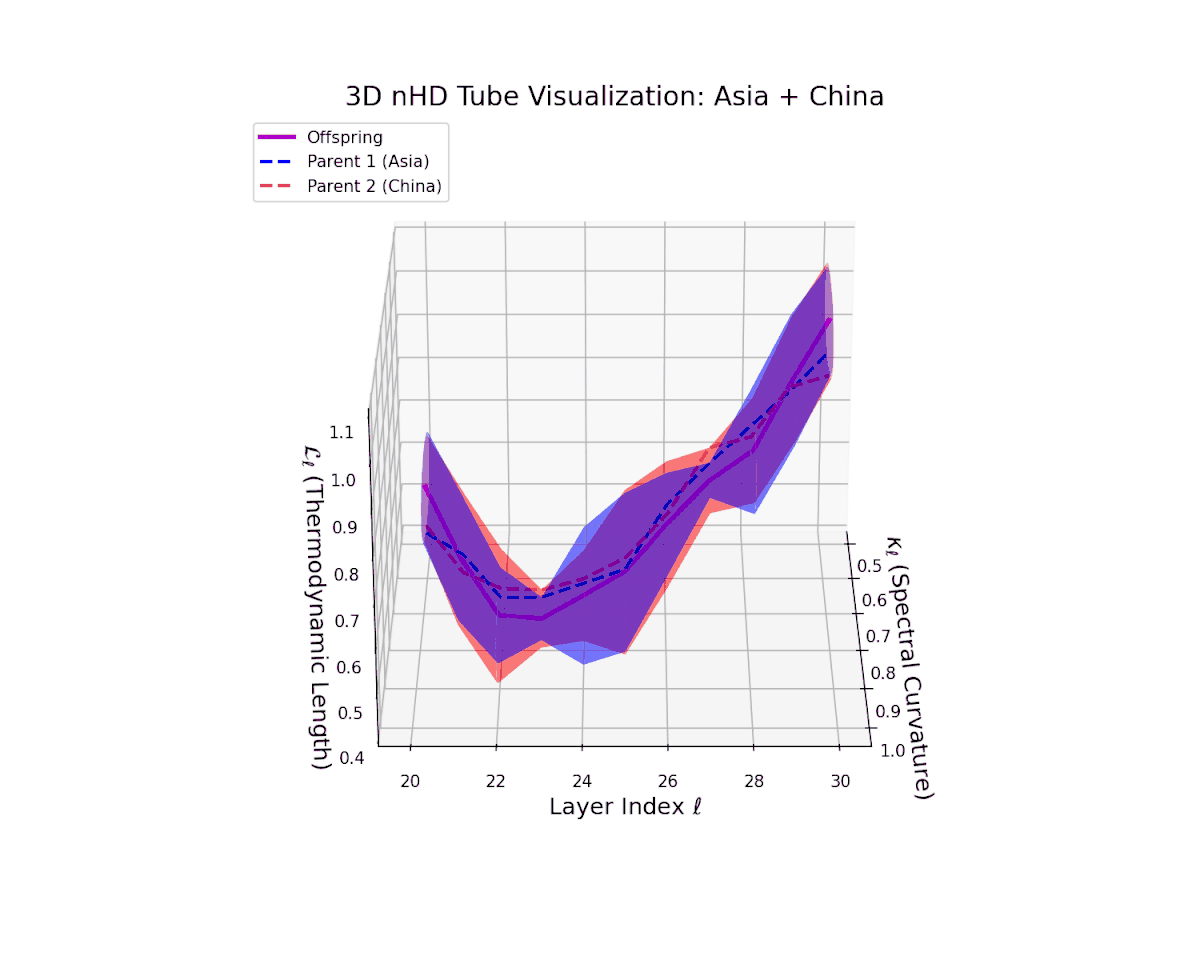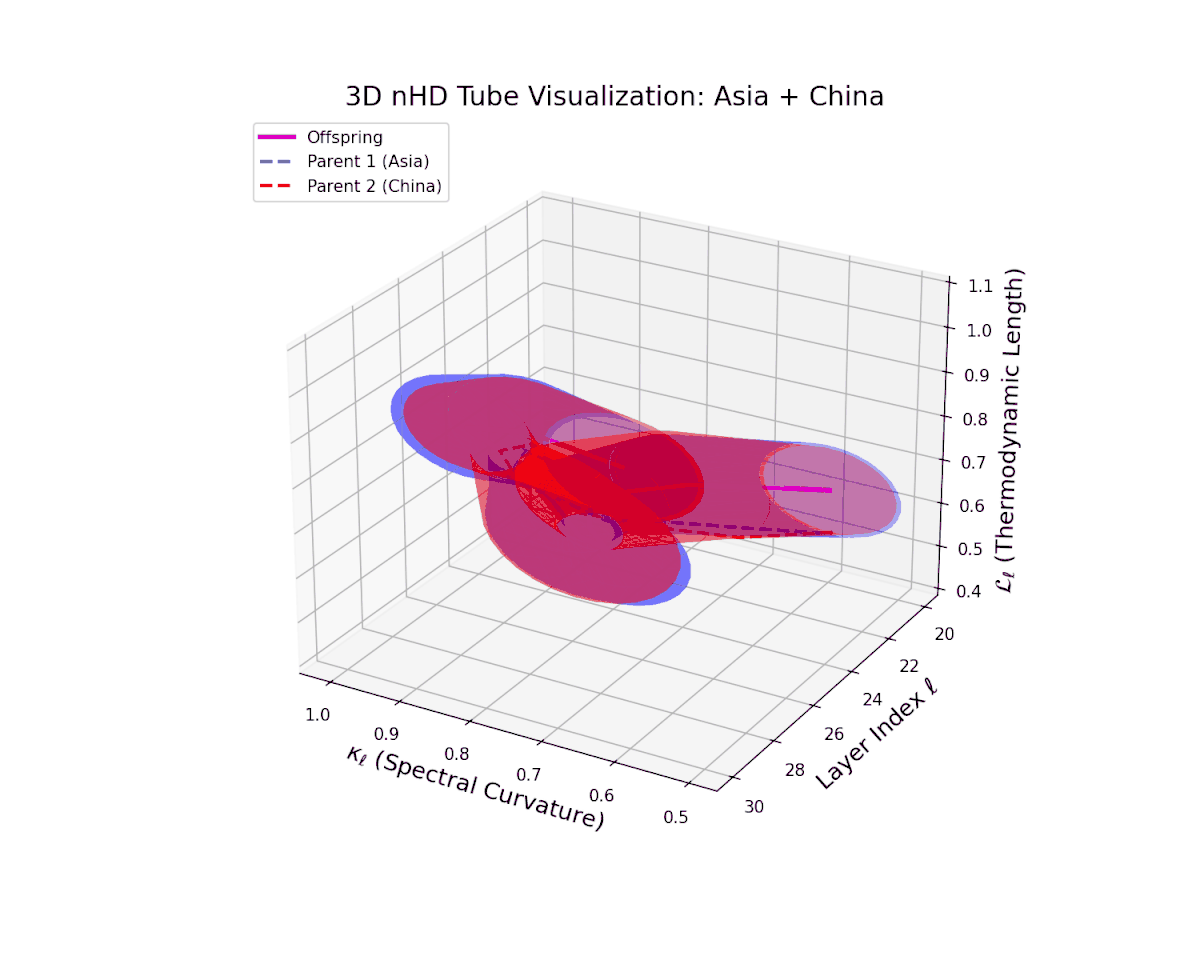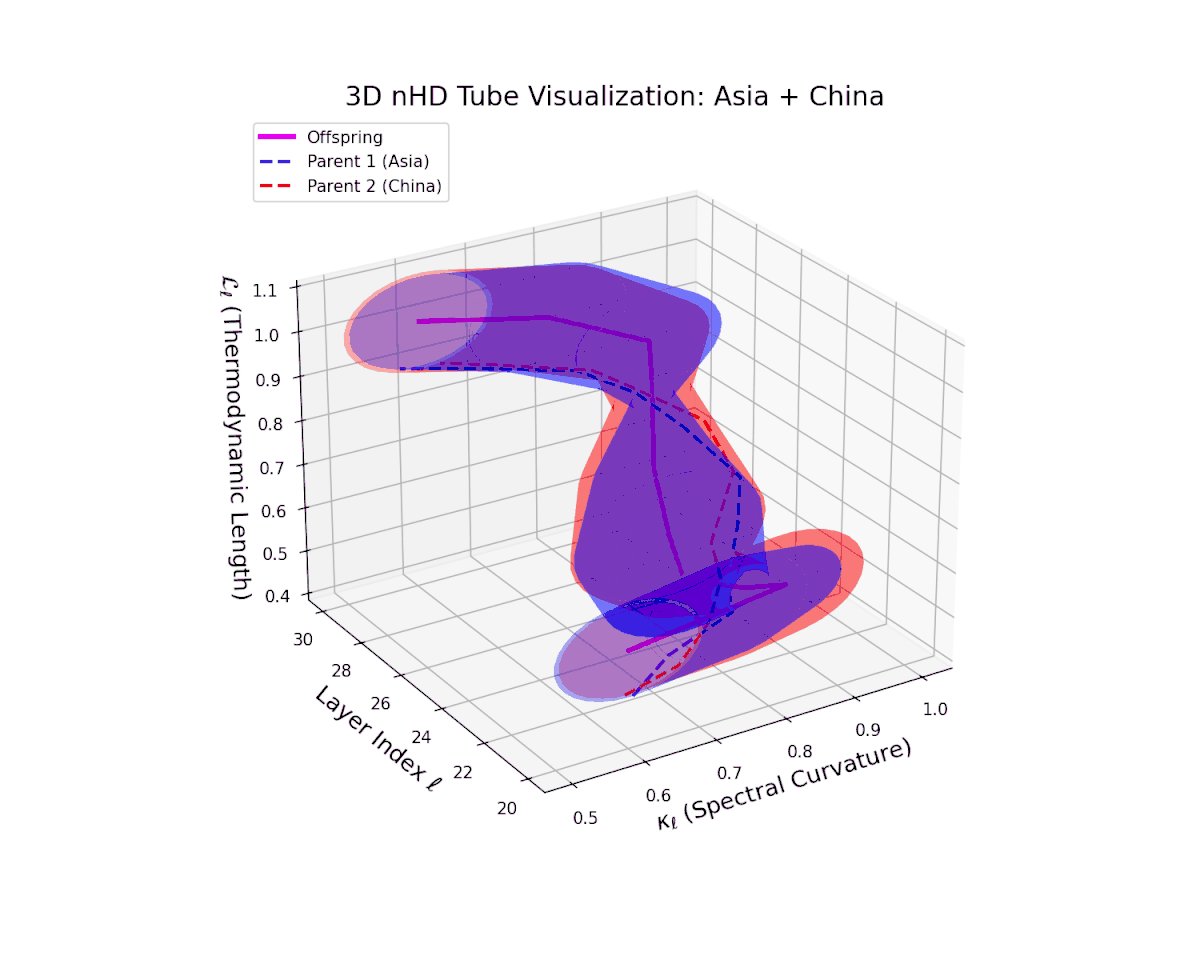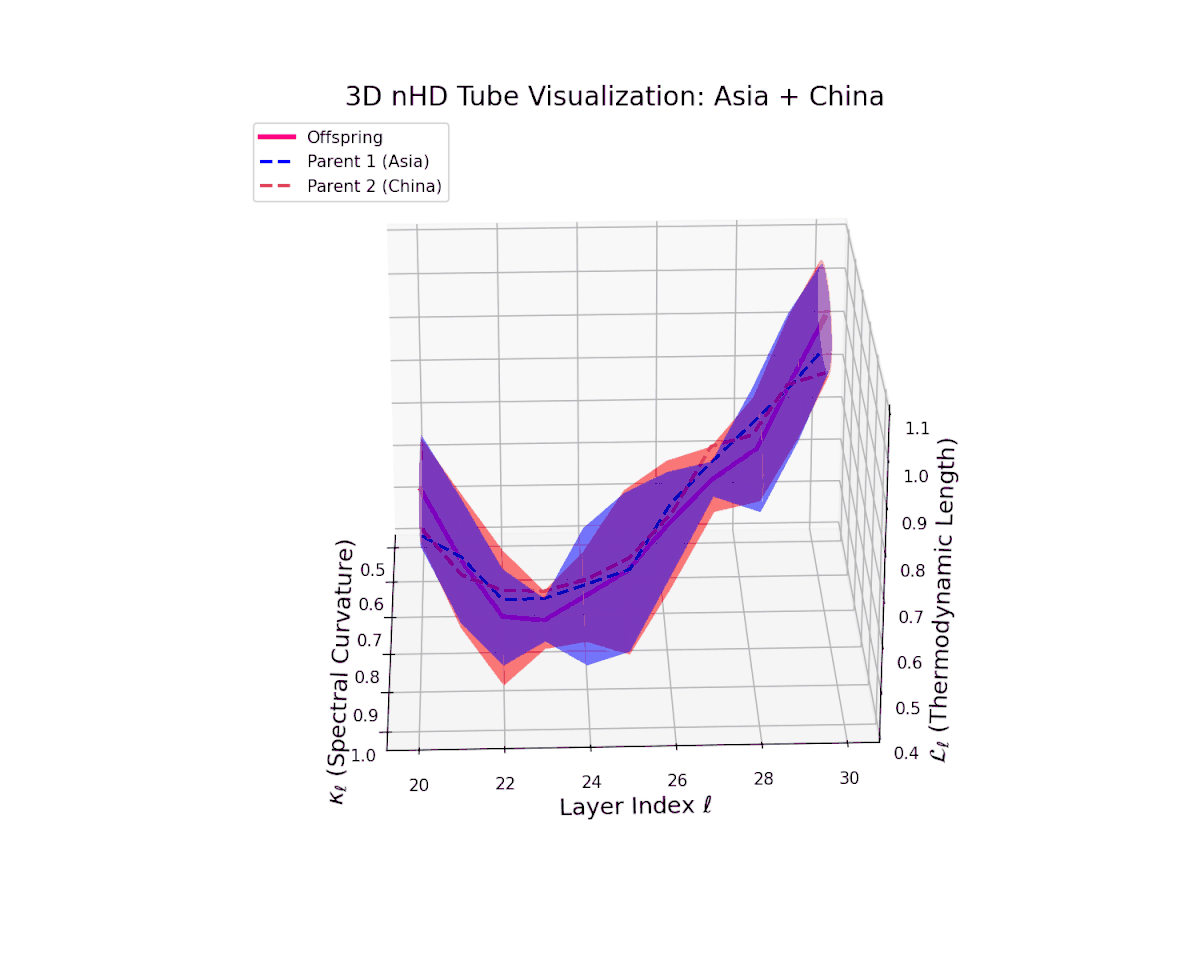
**(V) Asia–China Fusion**
The offspring latent manifold (magenta solid line) closely shadows the parental manifolds (dashed lines), with spectral curvature $\kappa_{\ell}$ rising steadily from $0.4$ to $0.9$. This reflects a notable increase in local nonlinear bending and representational complexity. Simultaneously, the thermodynamic length $L_{\ell}$, integrating the Fisher-Rao metric, extends from $0.45$ to $1.0$, marking significant cumulative semantic transformation. This close geometric match implies minimal distortion, strong cultural affinity, and shared latent subspaces, mirroring biological conserved genetic pathways.

**(VI) Asia–Latin America Fusion**
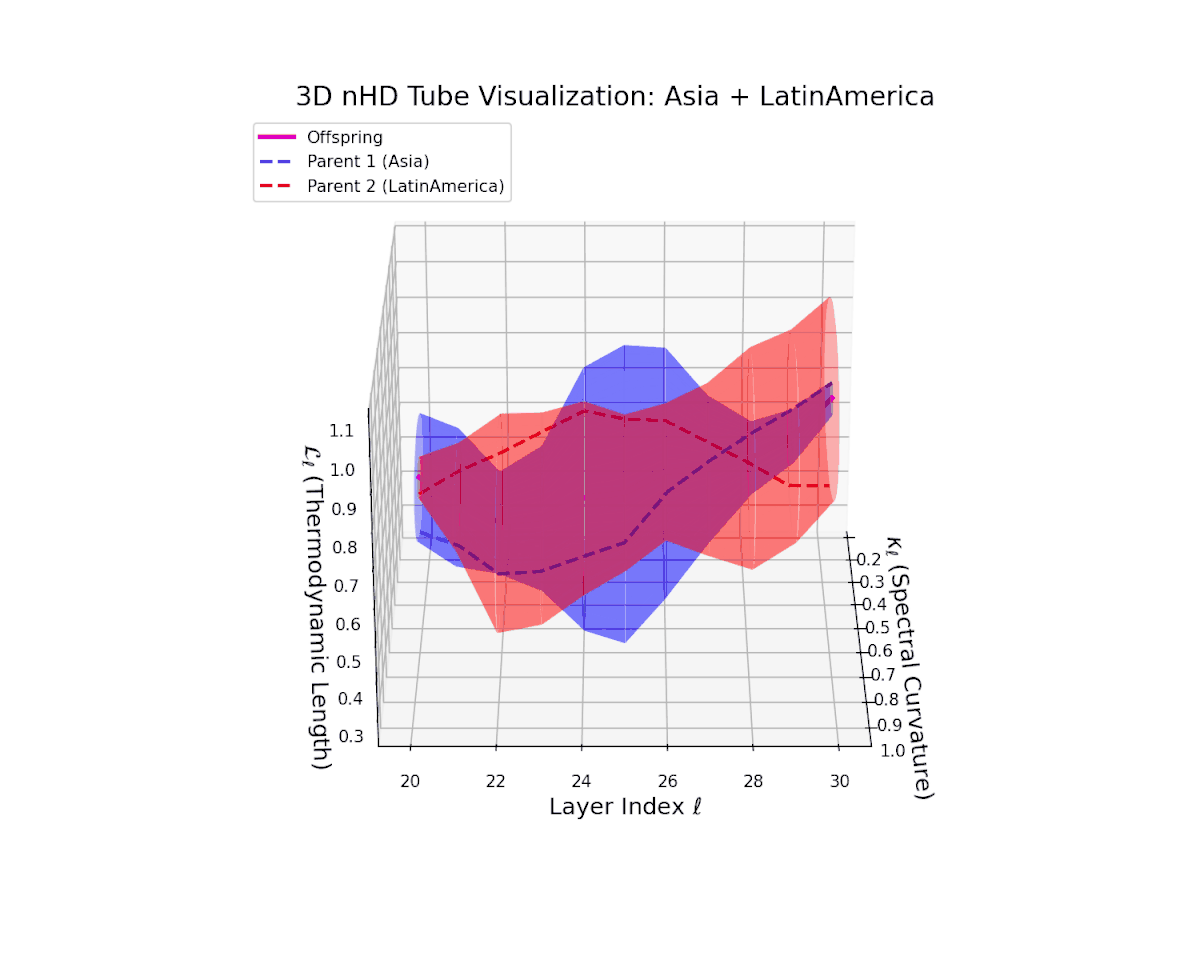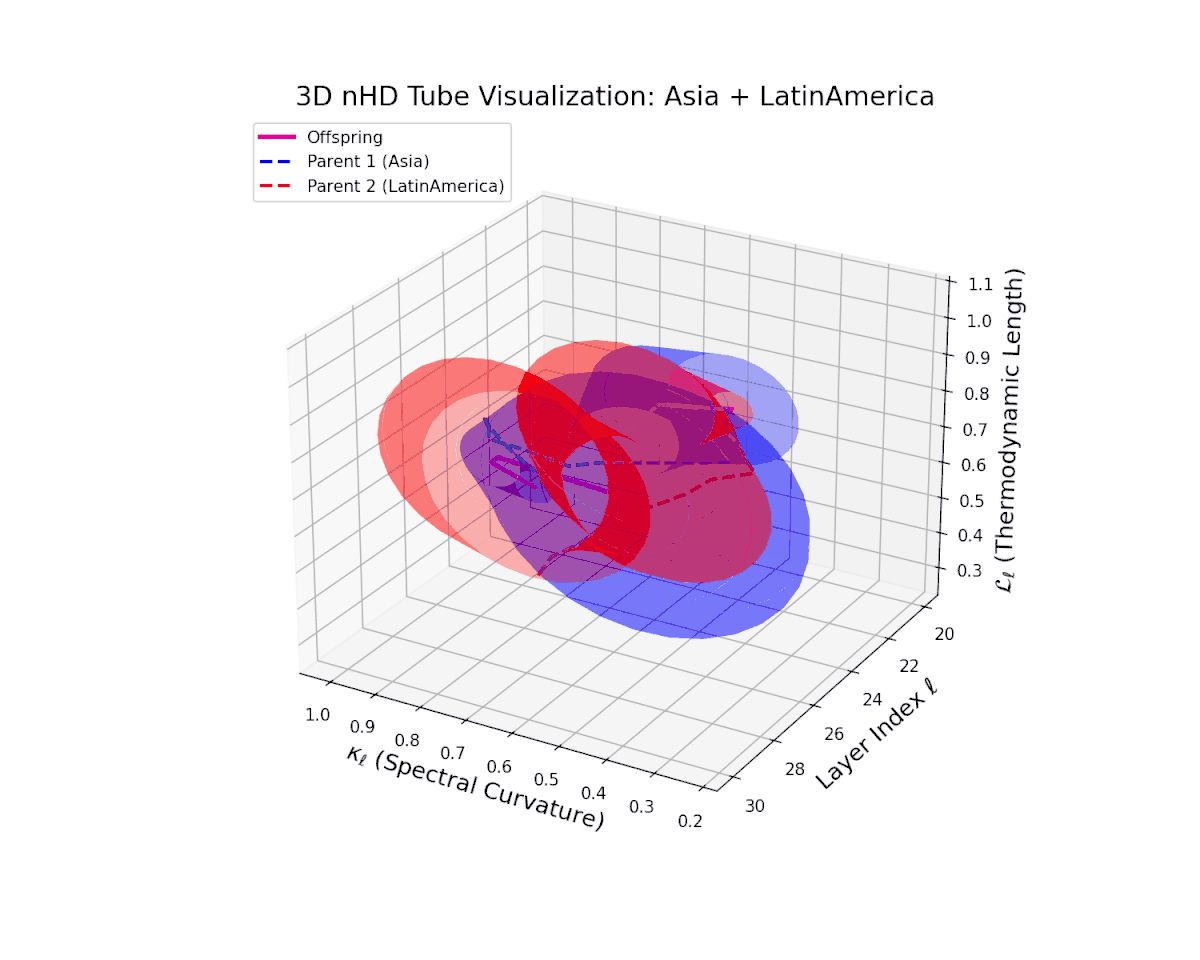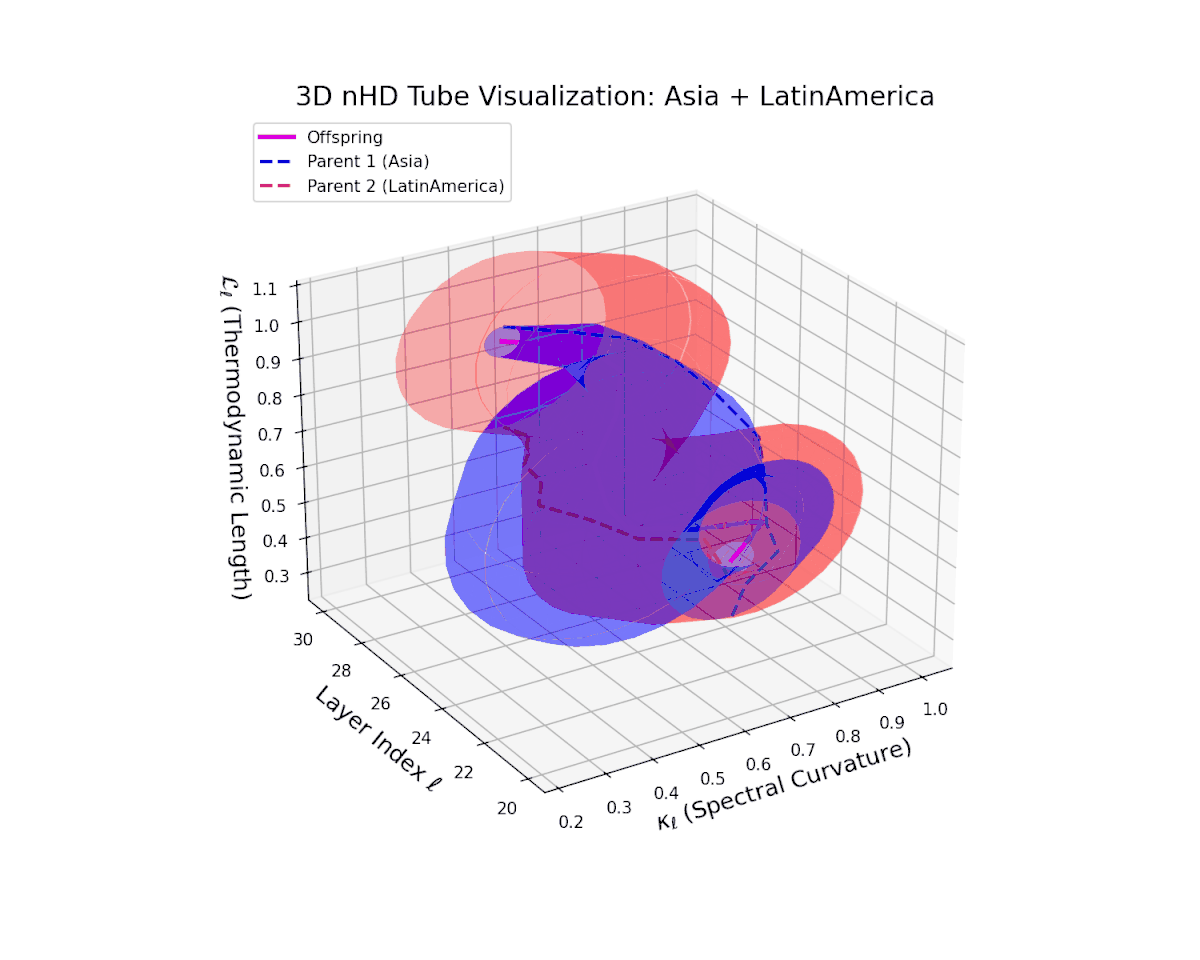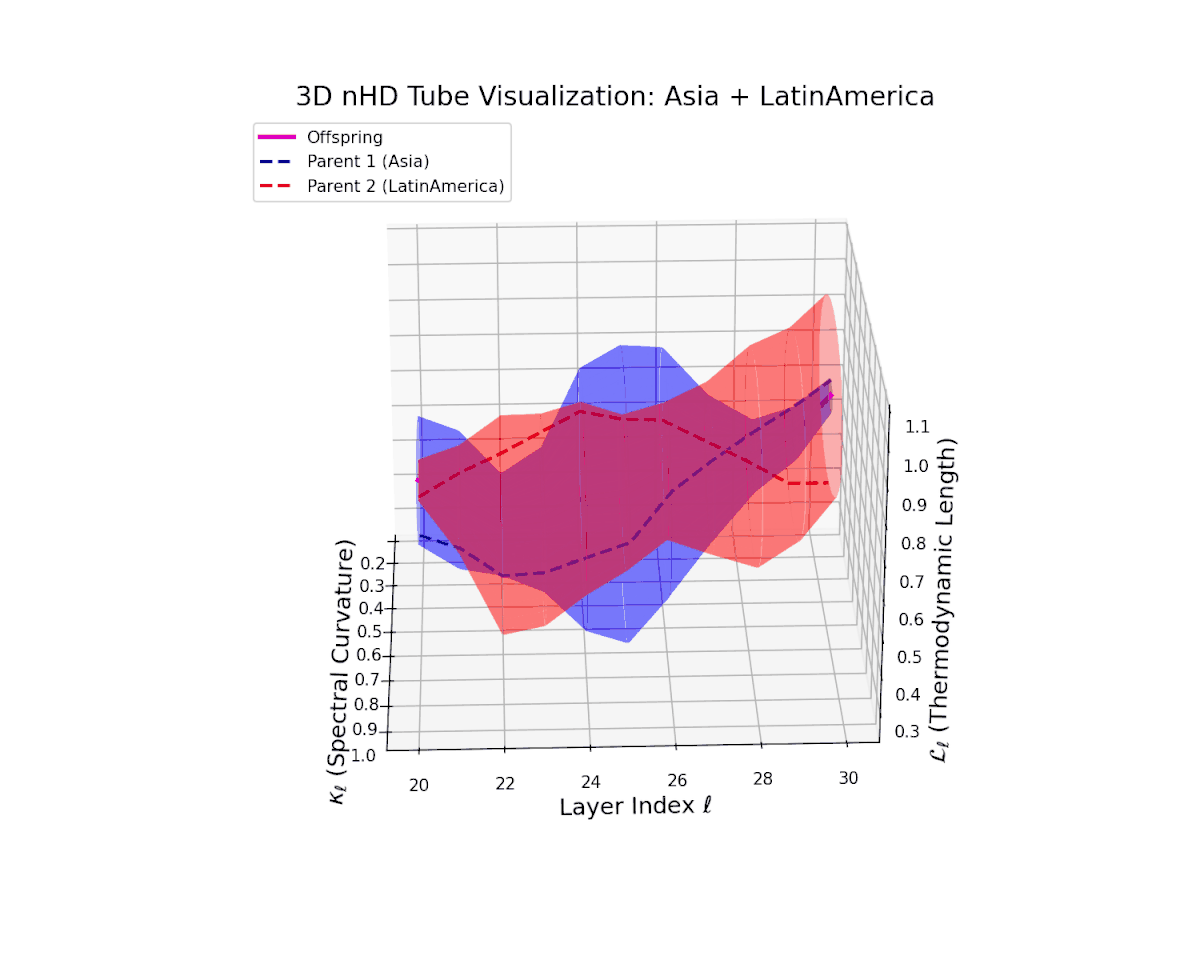
The offspring latent manifold shows a complex emergent semantic integration, with spectral curvature $\kappa_{\ell}$ rising from $0.3$ to $0.85$, indicating enhanced local manifold bending and nonlinear compositionality. The thermodynamic length $L_{\ell}$ grows from $0.4$ to $0.95$, quantifying cumulative semantic changes along evolving latent trajectories. This geometric expansion reflects a progressive fusion of culturally distinct yet semantically complementary neural DNAs, creating a richly layered latent space akin to biological recombination processes.

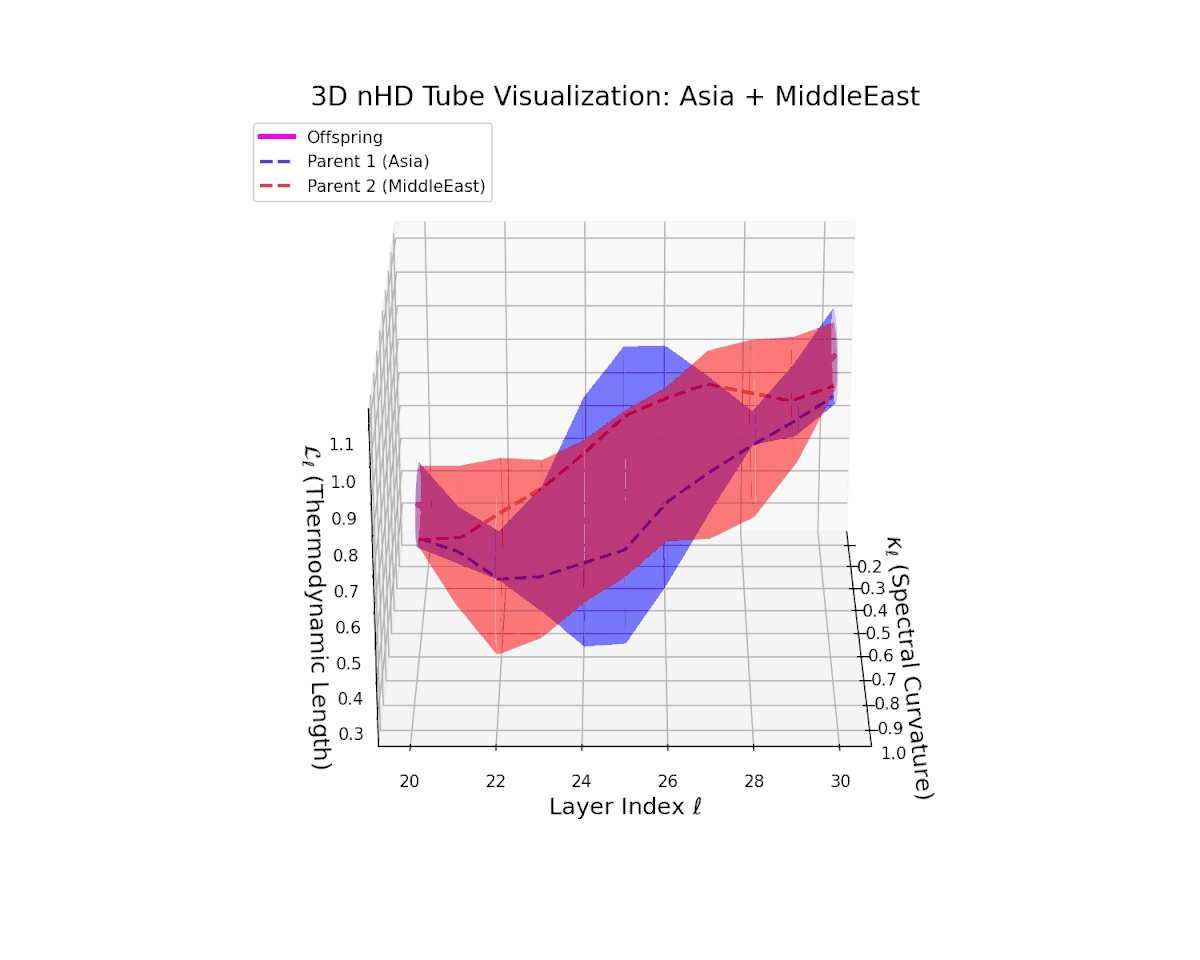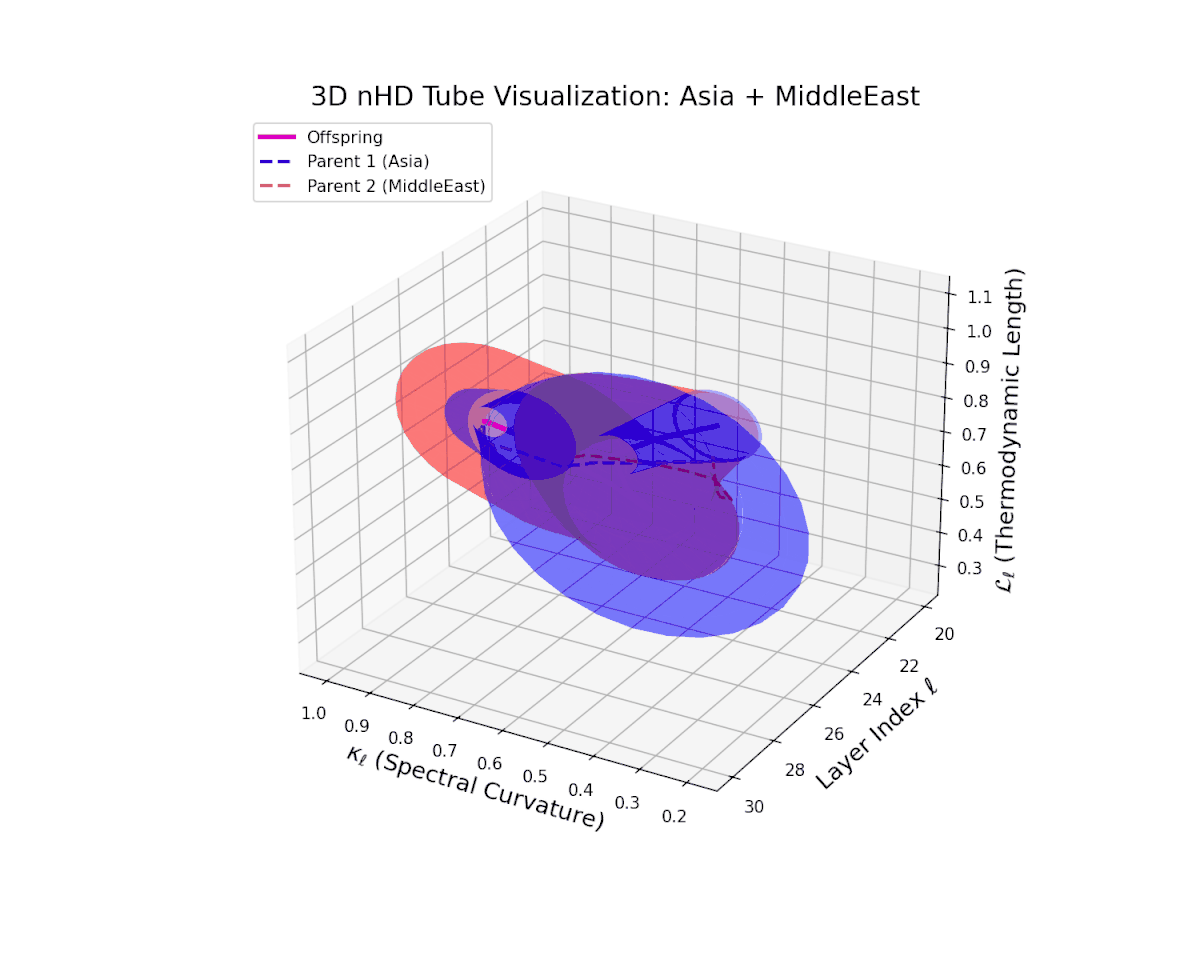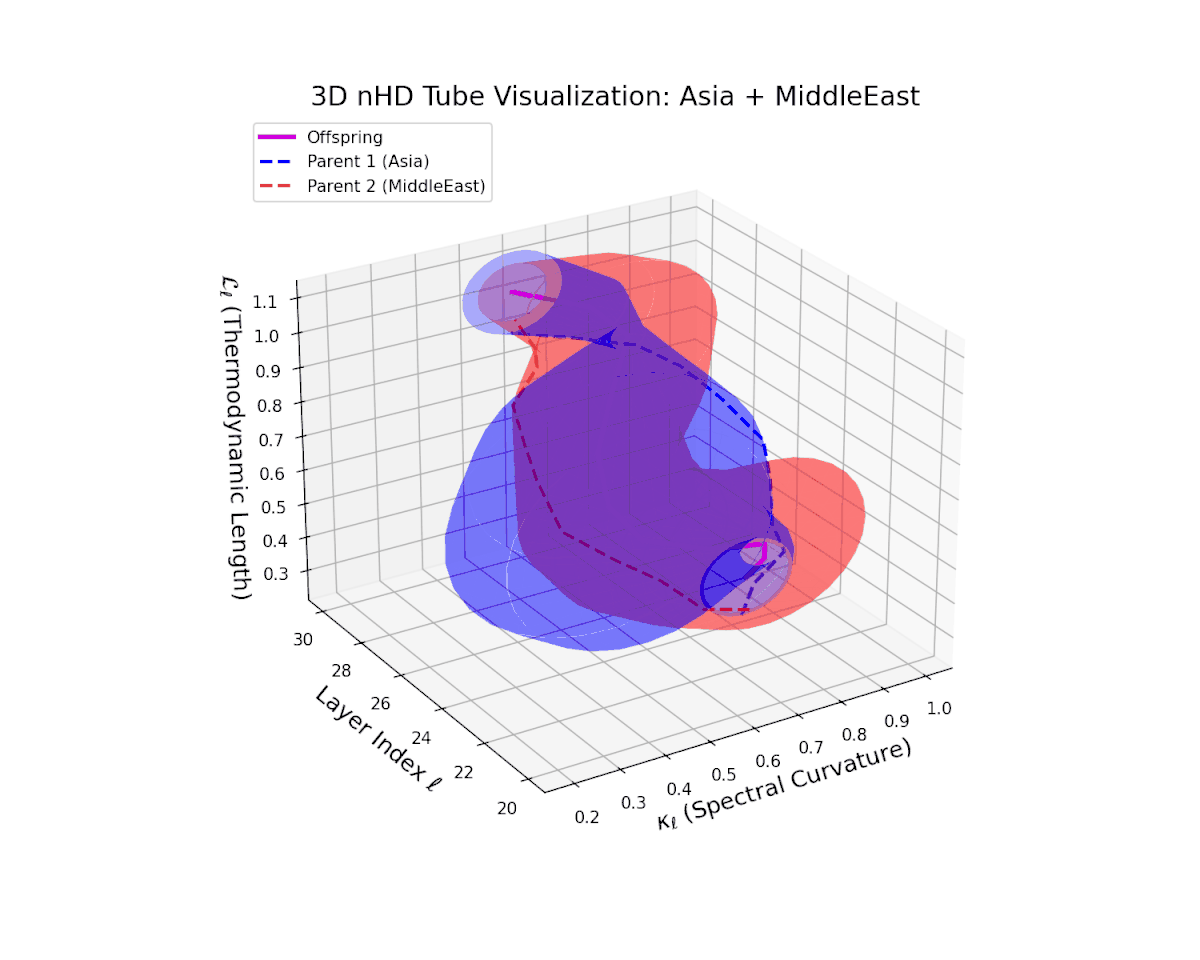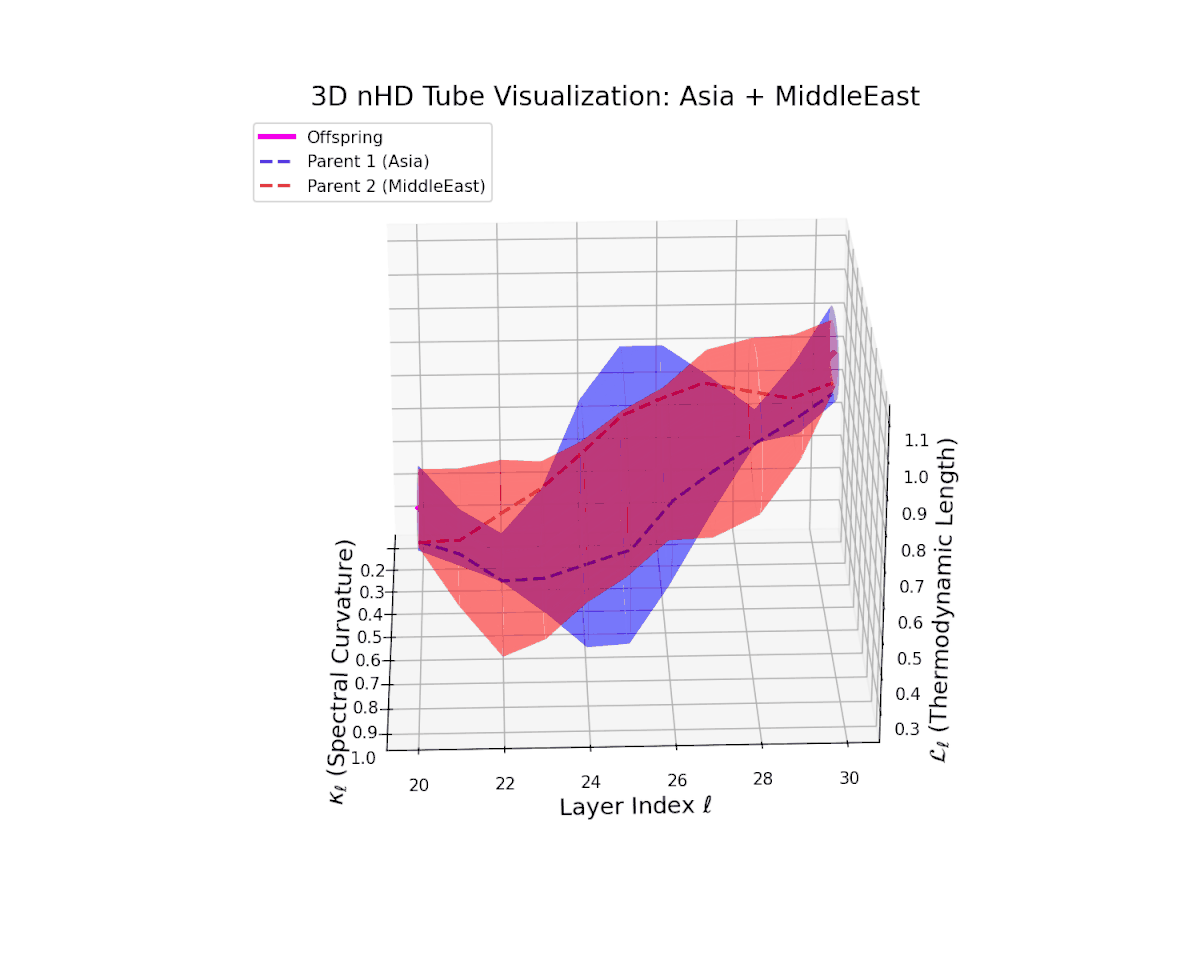
**(VII) Asia–Middle East Fusion**
The offspring latent manifold shows a pronounced increase in spectral curvature $\kappa_{\ell}$, from $0.35$ to $0.85$, reflecting substantial nonlinear bending and enhanced latent complexity. The thermodynamic length $L_{\ell}$ extends from $0.5$ to $1.05$, marking a significant cumulative semantic transformation indicative of intricate fusion dynamics. These geometric signatures reveal a complex interplay producing smooth yet richly curved trajectories. This structural reshaping illustrates how heterogeneous semantic priors blend to form novel, robust representations, akin to epistatic interactions generating emergent phenotypic traits.

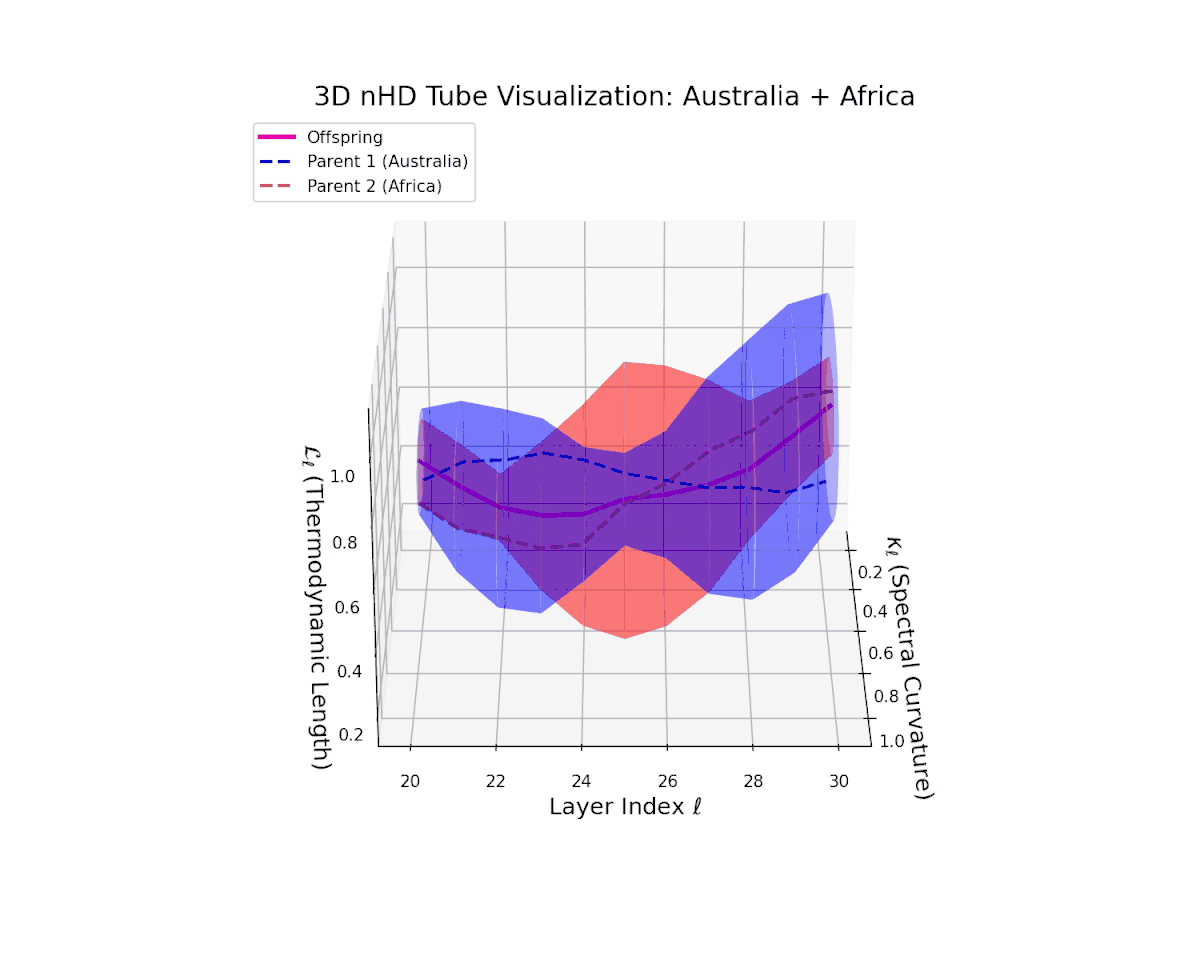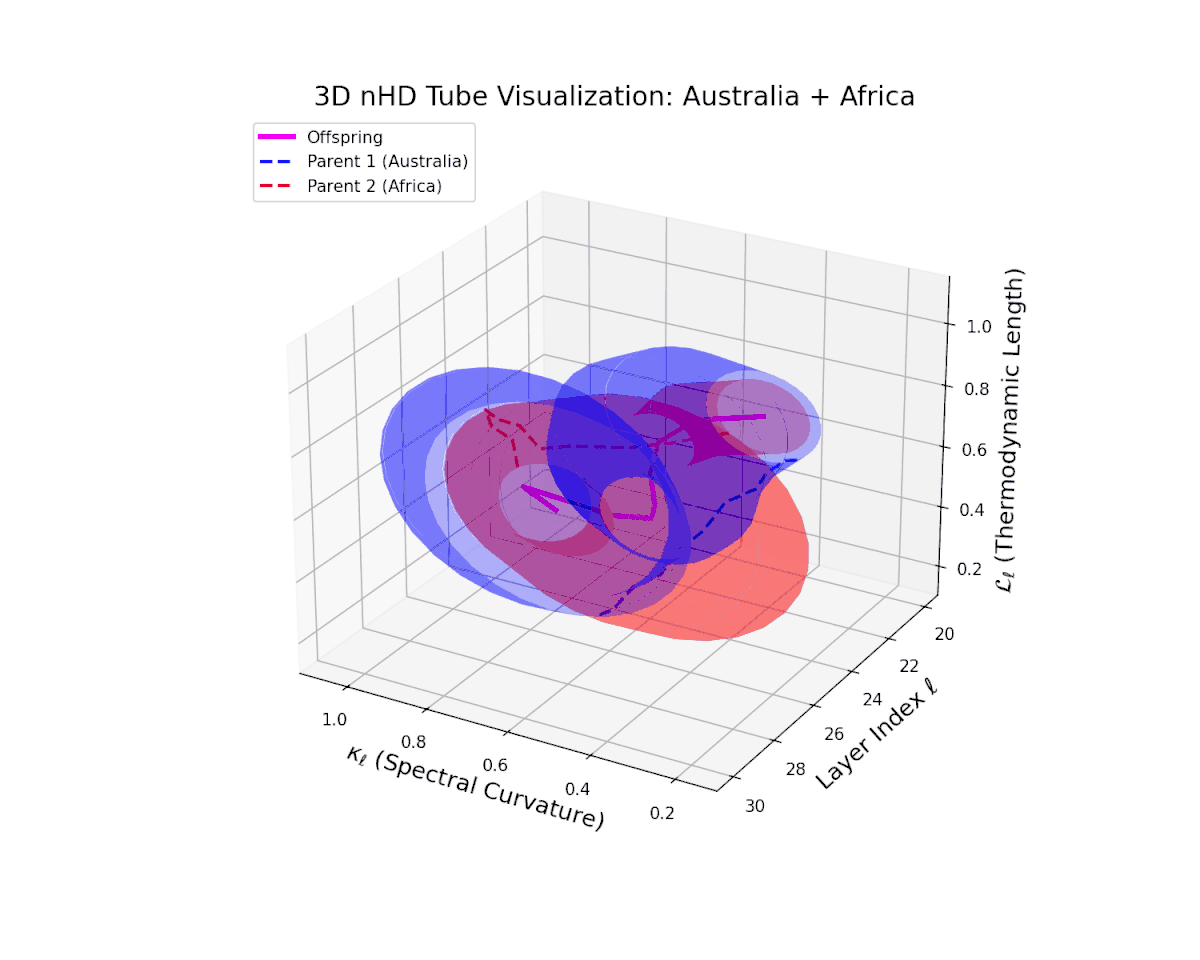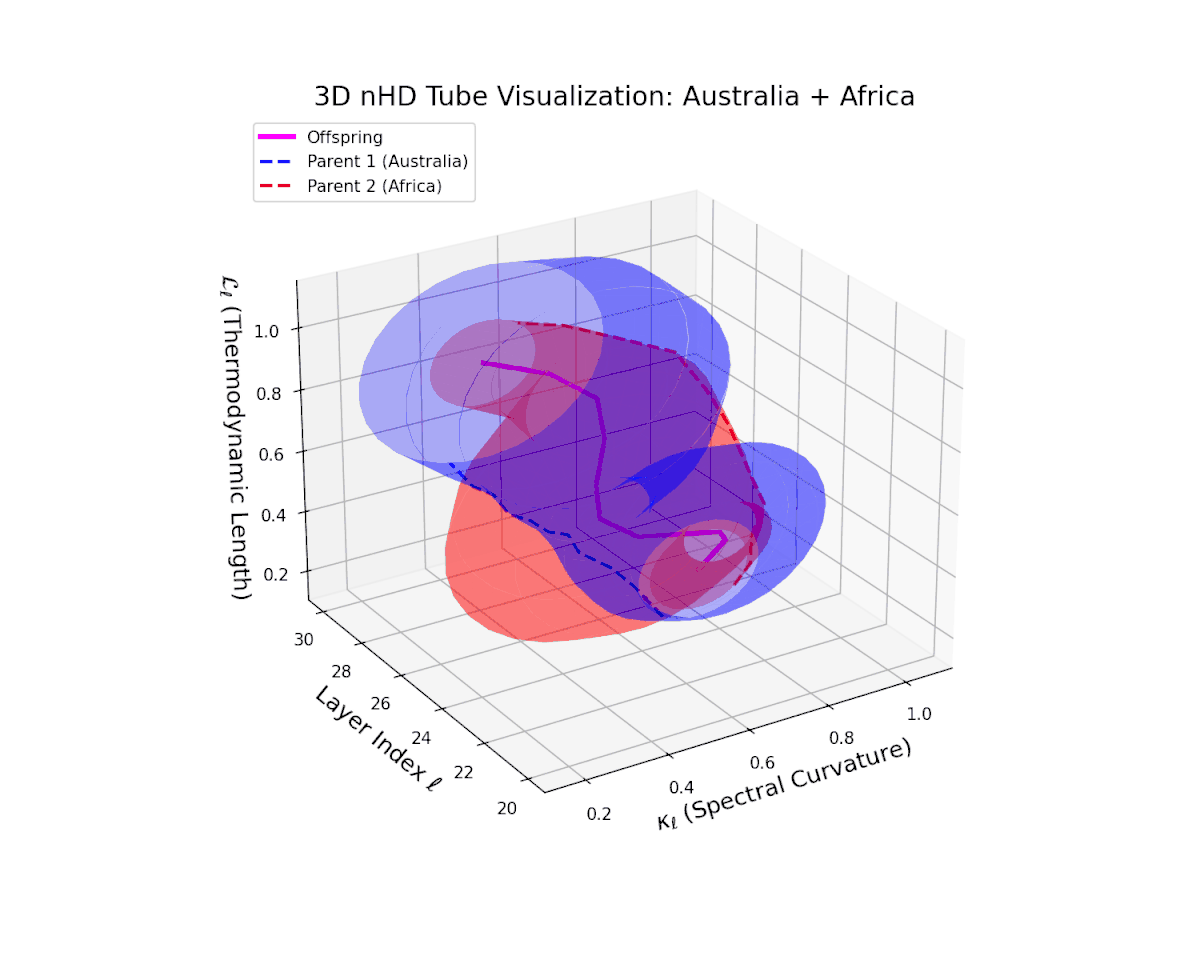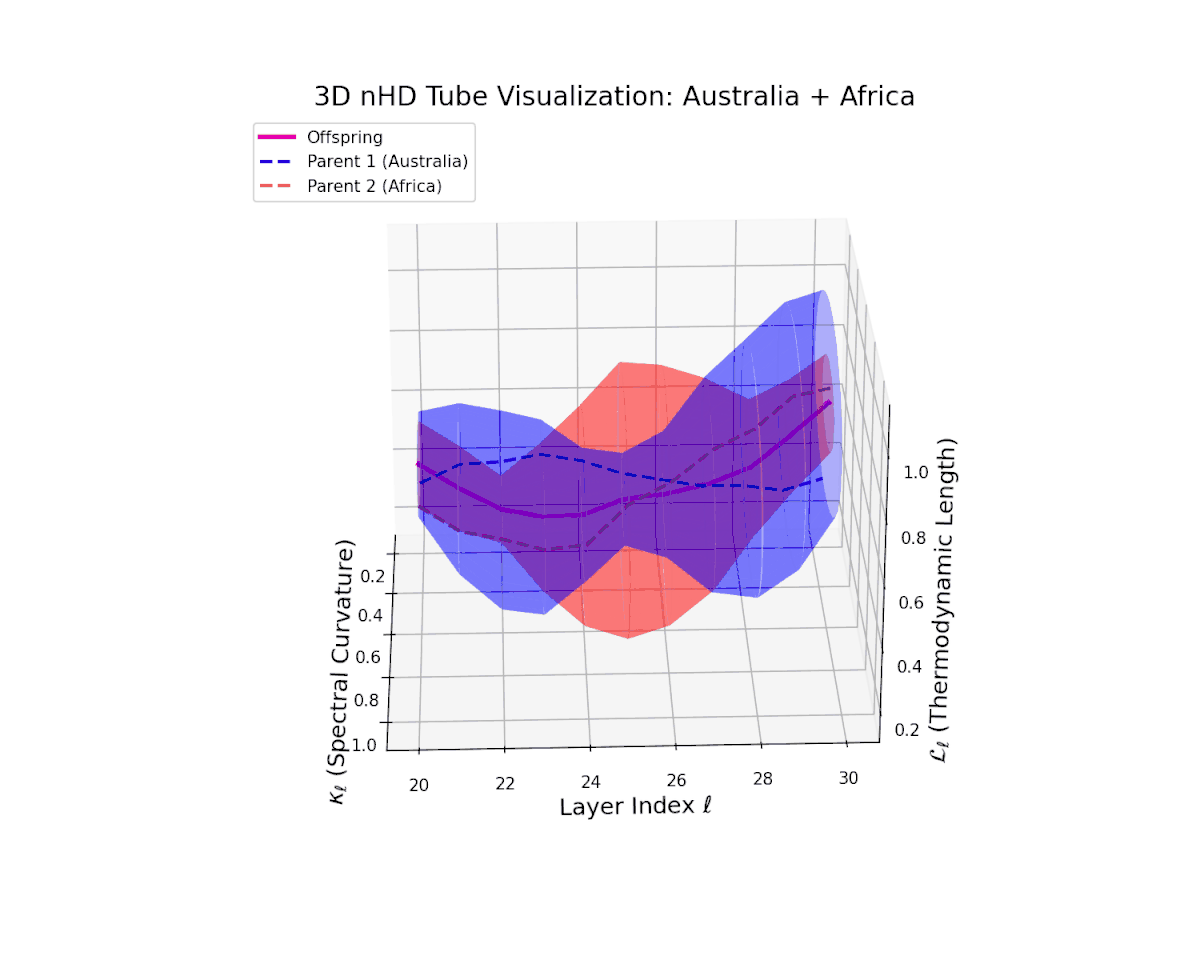
**(VIII) Australia–Africa Fusion**
The offspring latent manifold (magenta) smoothly interpolates between parental latent spaces, with spectral curvature $\kappa_{\ell}$ ascending from $0.3$ to $0.7$, indicating growing local manifold nonlinearity and complexity. The thermodynamic length $L_{\ell}$ rises from $0.35$ to $0.85$, capturing cumulative semantic evolution. This continuous trajectory reflects a stable, coherent semantic fusion, showing how distinct cultural neural DNAs integrate seamlessly, preserving manifold smoothness and enabling rich representational expressivity. This pattern parallels biological genetic recombination conserving core functions while enabling adaptive innovation.

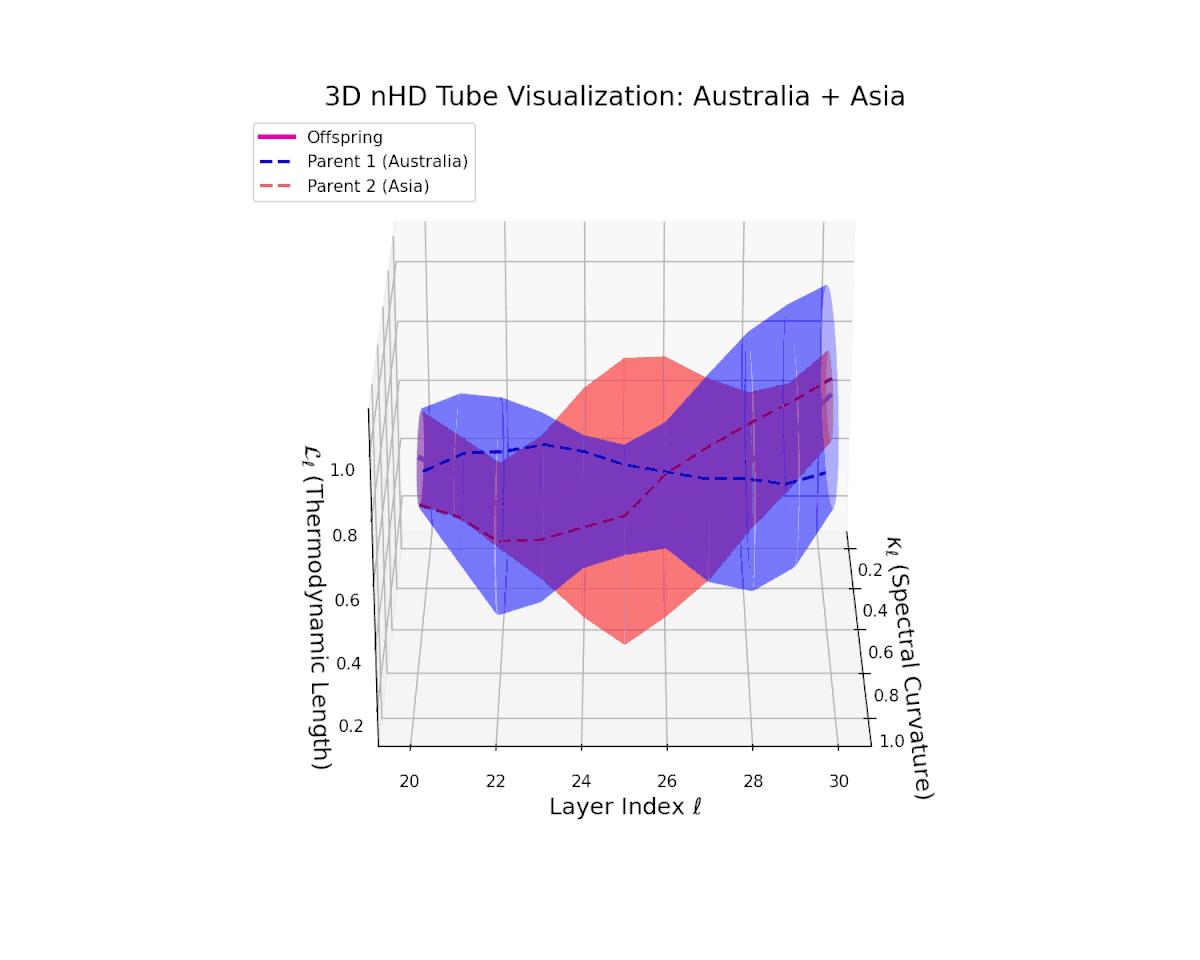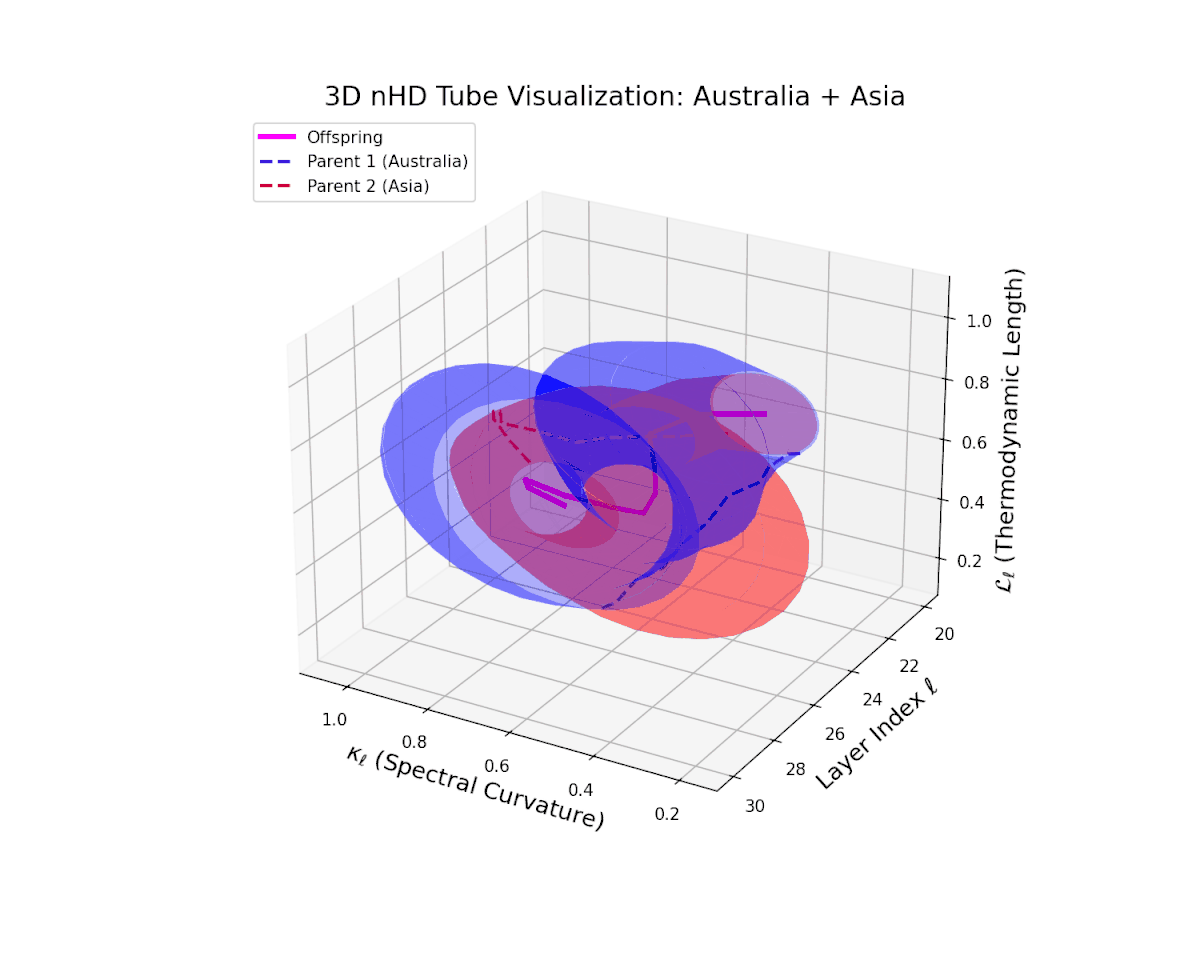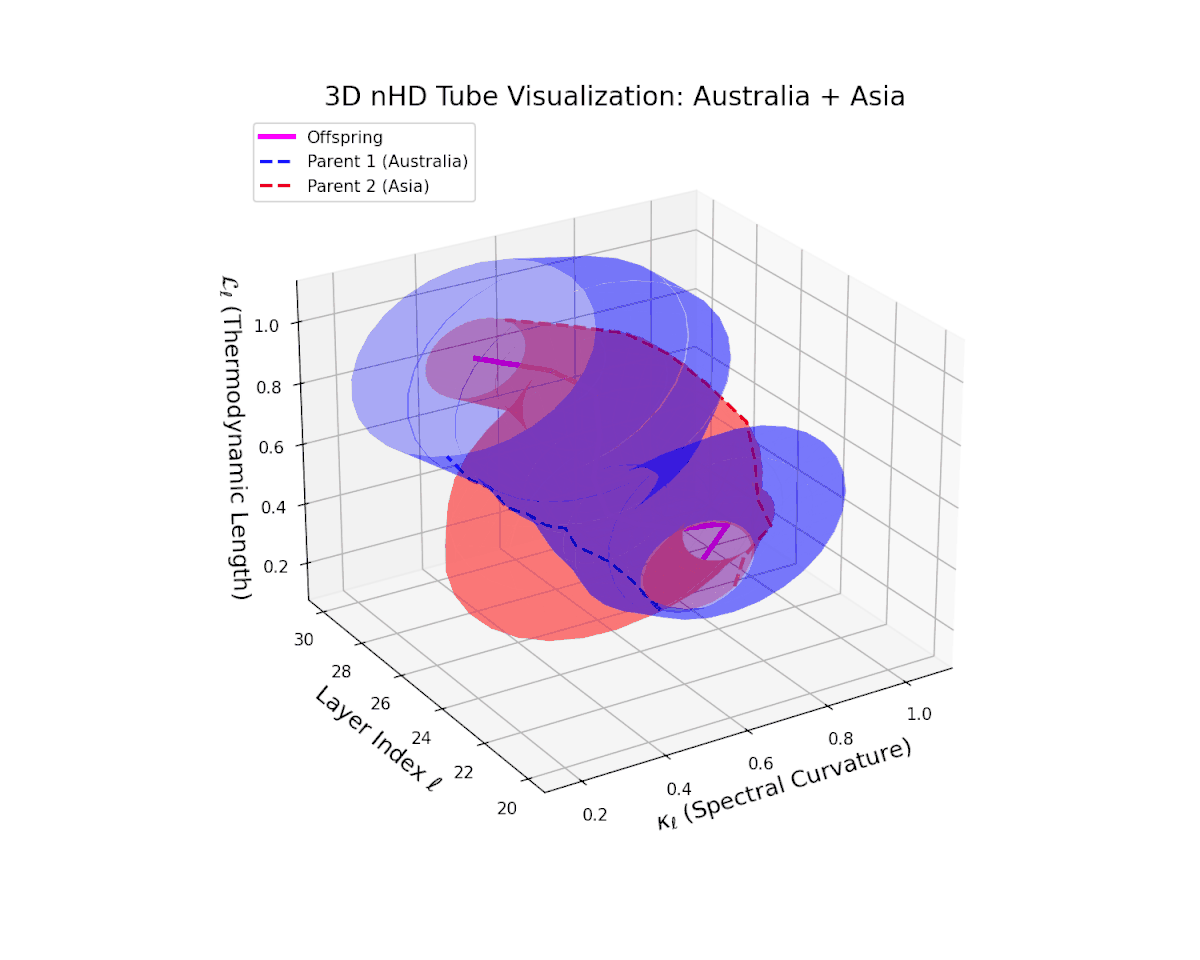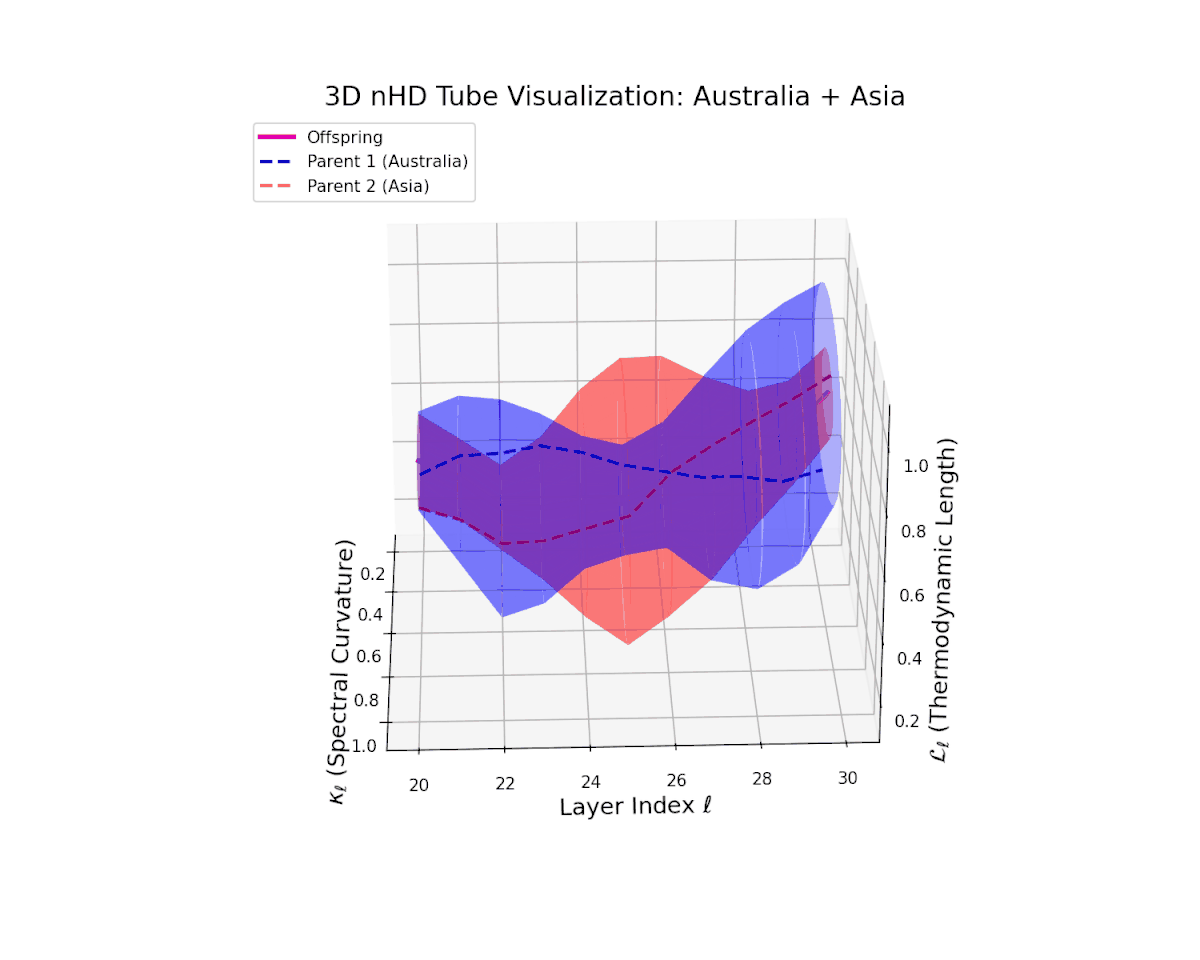
**(IX) Australia–Asia Fusion**
The offspring latent manifold (magenta solid) smoothly interpolates between parental manifolds (dashed lines), tracing a continuous and coherent path over transformer layers $\ell = 20$ to $30$. The spectral curvature $\kappa_{\ell}$ increases steadily from approximately $0.25$ to $0.75$, indicating a gradual enrichment of local nonlinear geometric complexity within the latent space. Simultaneously, the thermodynamic length $L_{\ell}$, measuring cumulative semantic representational change via the Fisher-Rao metric, grows from about $0.4$ to $0.9$. This pattern reflects a sophisticated hierarchical fusion of semantic features and information geometry across deep transformer layers, exemplifying smooth integration of distinct cultural neural DNAs.

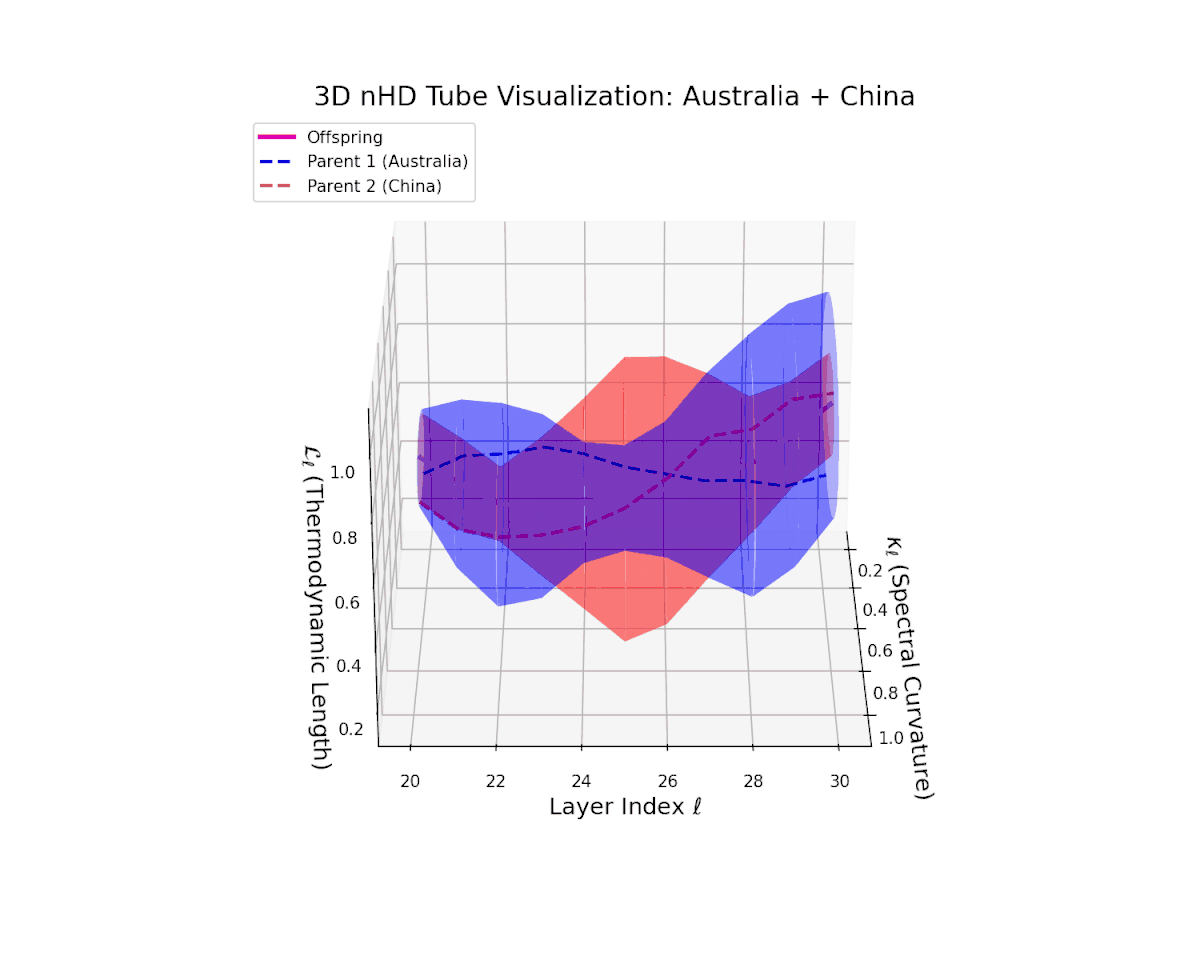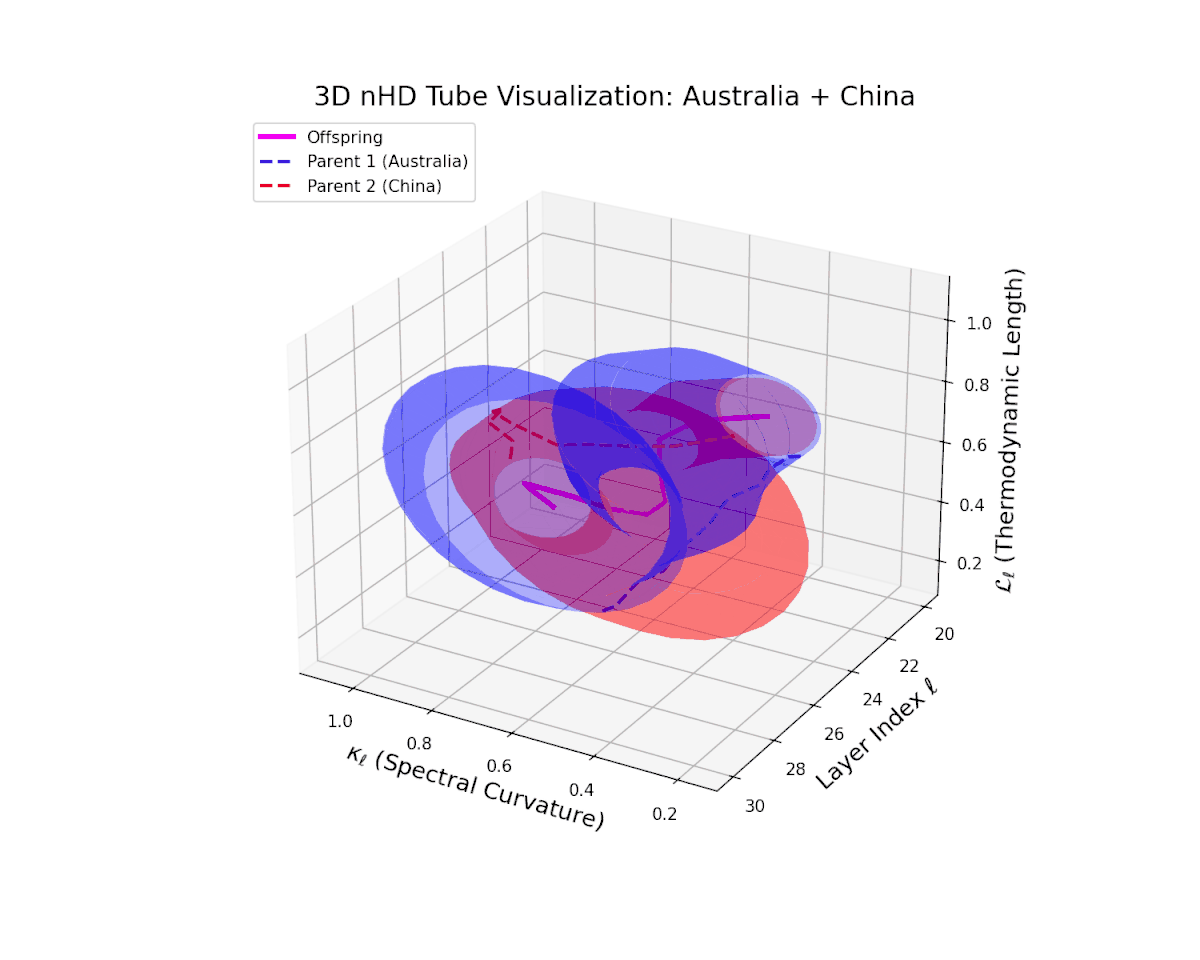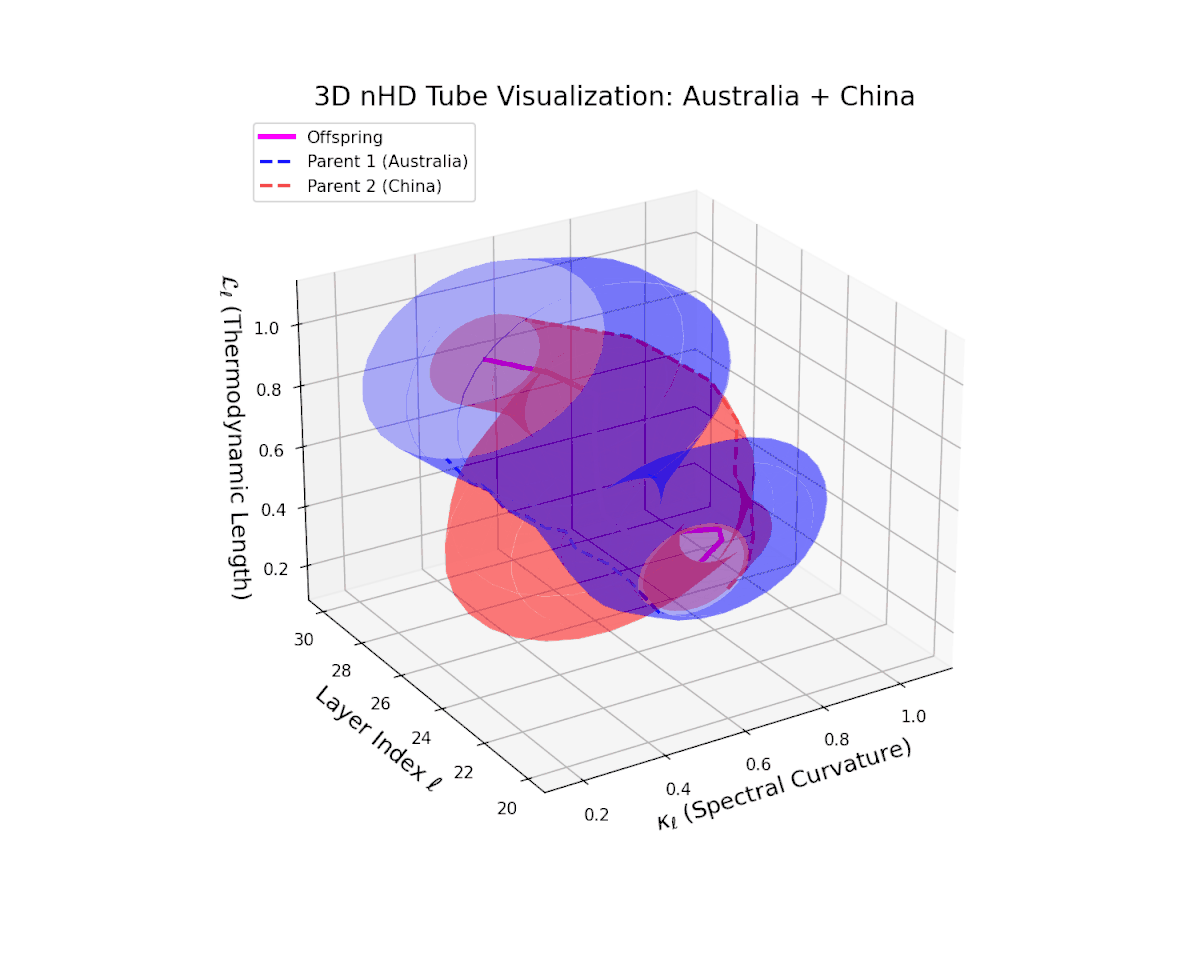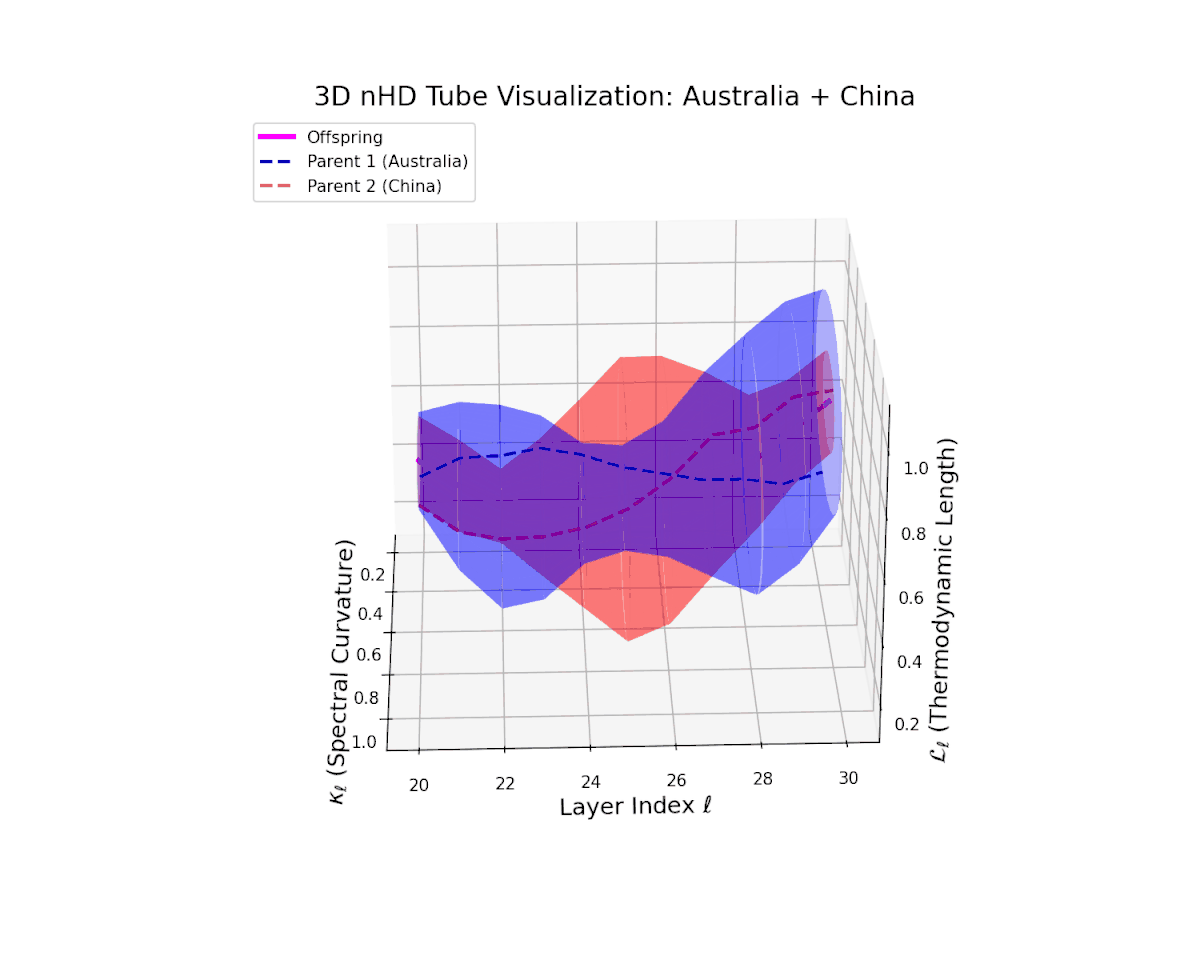
**(X) Australia–China Fusion**
The offspring manifold (magenta solid) occupies the convex latent space defined by its parental manifolds, indicating a complex yet continuous semantic fusion. The spectral curvature $\kappa_{\ell}$ rises steadily from approximately $0.3$ to $0.8$, reflecting increased nonlinear manifold bending and latent representational intricacy. Concurrently, the thermodynamic length $L_{\ell}$ extends from $0.35$ to $0.95$, revealing an extended Fisher-Rao geodesic length that signifies layered semantic transformation and cumulative information divergence in the deeper transformer layers. This smooth evolution captures nuanced blending of culturally distinct semantic features.

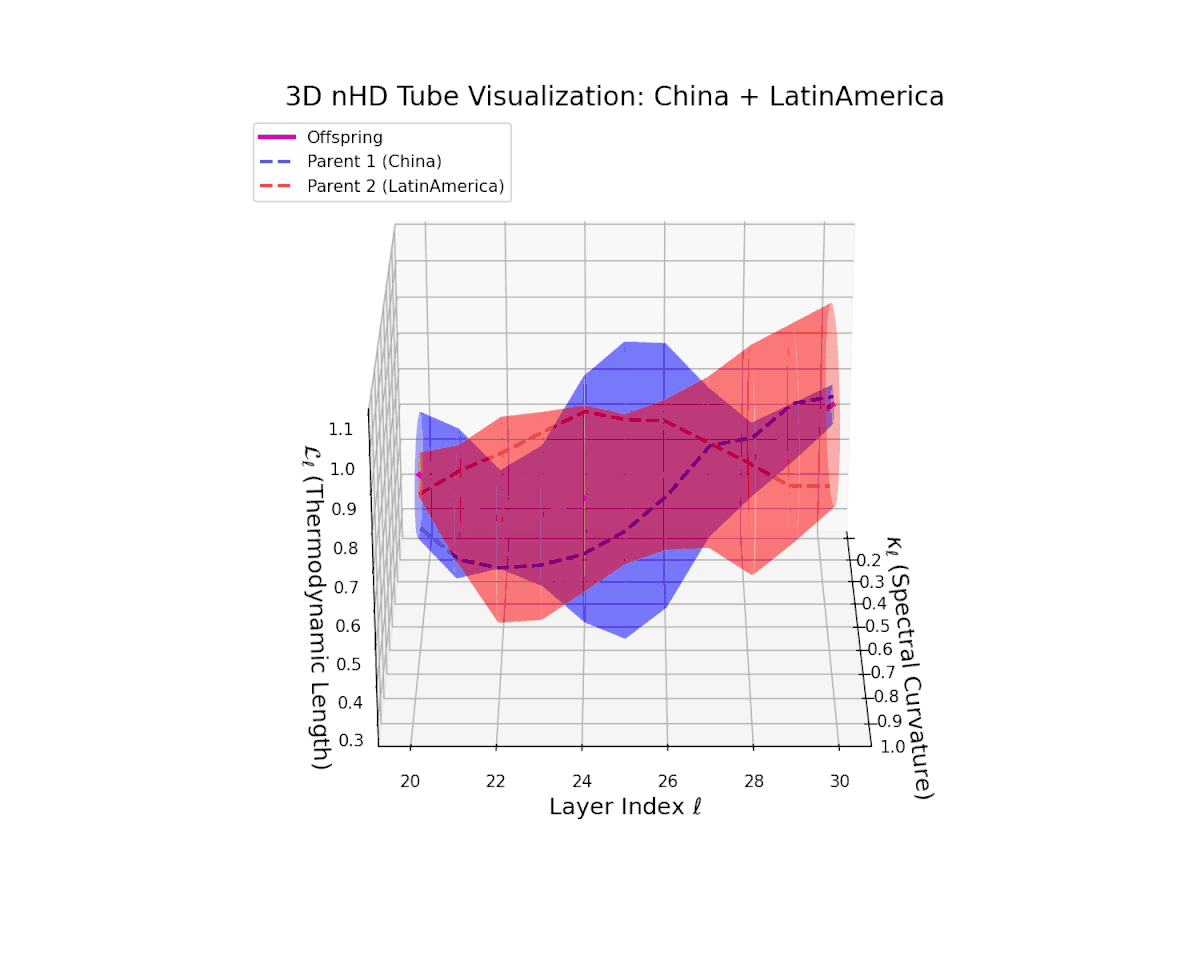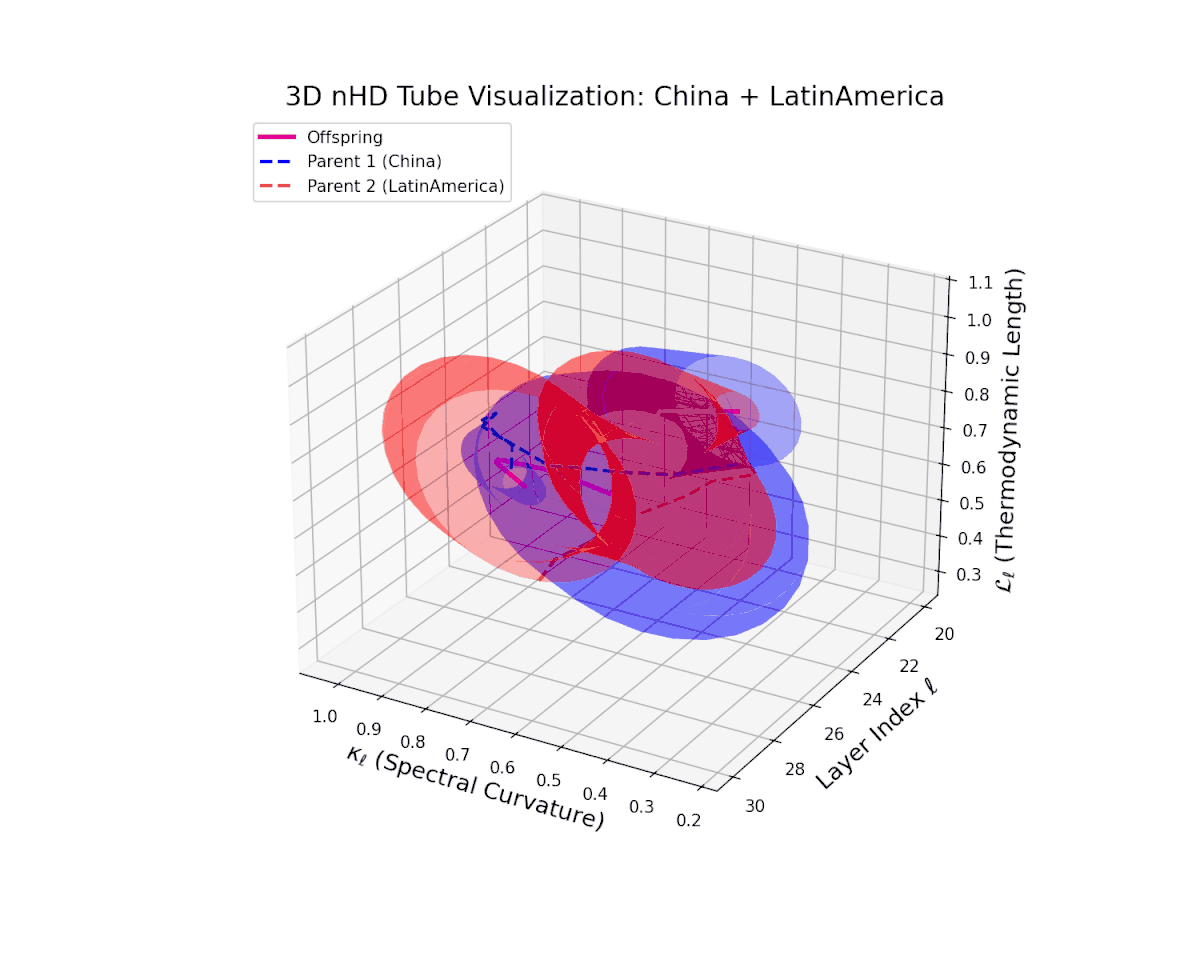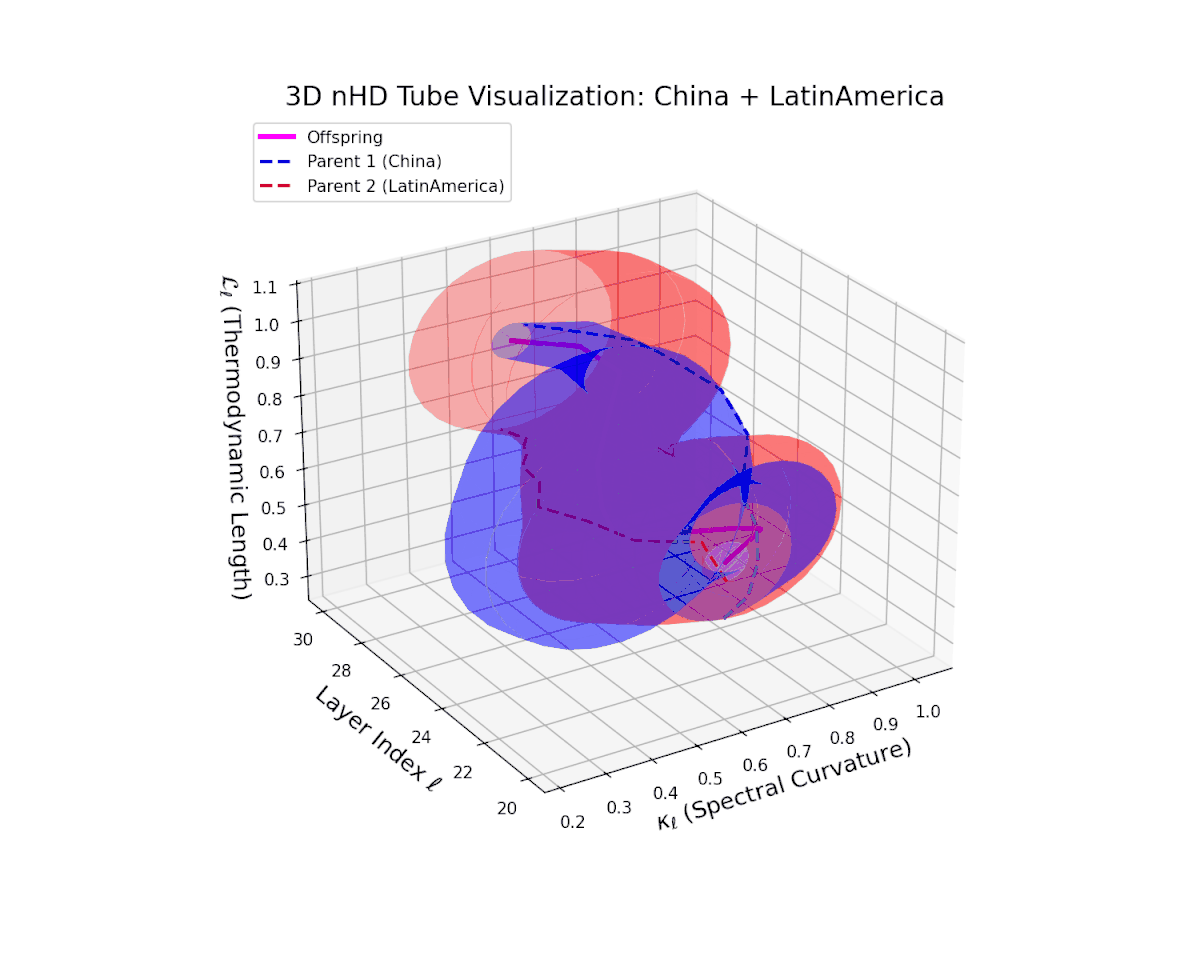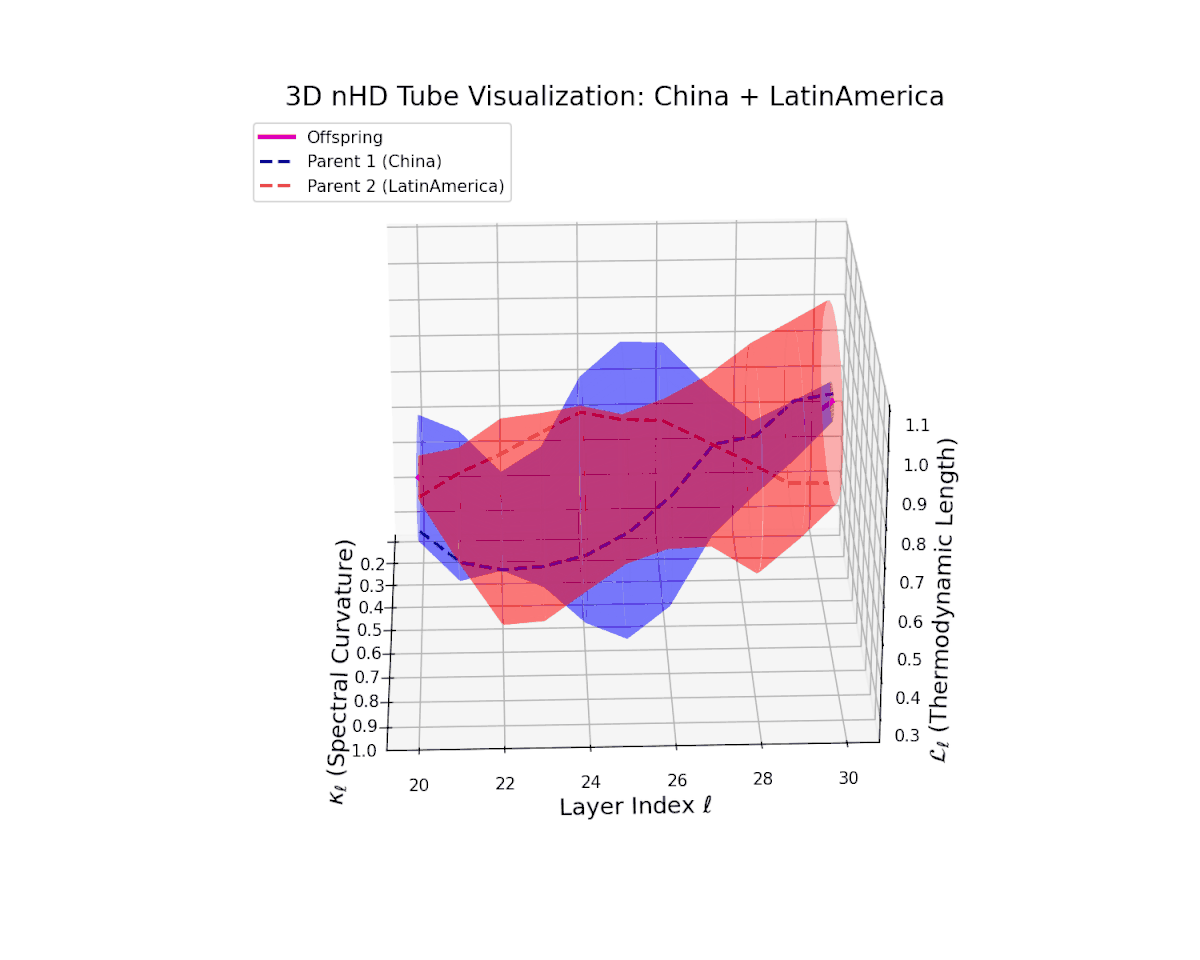
**(XI) China–Latin America Fusion**
The offspring latent manifold (magenta) resides strictly within the convex hull of parental manifolds (China in blue dashed, Latin America in red dashed), exhibiting a rich geometric interplay. Spectral curvature $\kappa_{\ell}$ evolves smoothly from $0.3$ to $0.8$, indicating increasingly complex local manifold bending as the transformer depth increases. Meanwhile, the thermodynamic length $L_{\ell}$ spans from $0.45$ to $0.95$, signifying a progressively extended cumulative semantic change along the Fisher-Rao geodesic. This reflects emergent nonlinear compositionality and hierarchical semantic fusion occurring within the model’s deep layers, blending diverse cultural neural DNAs.

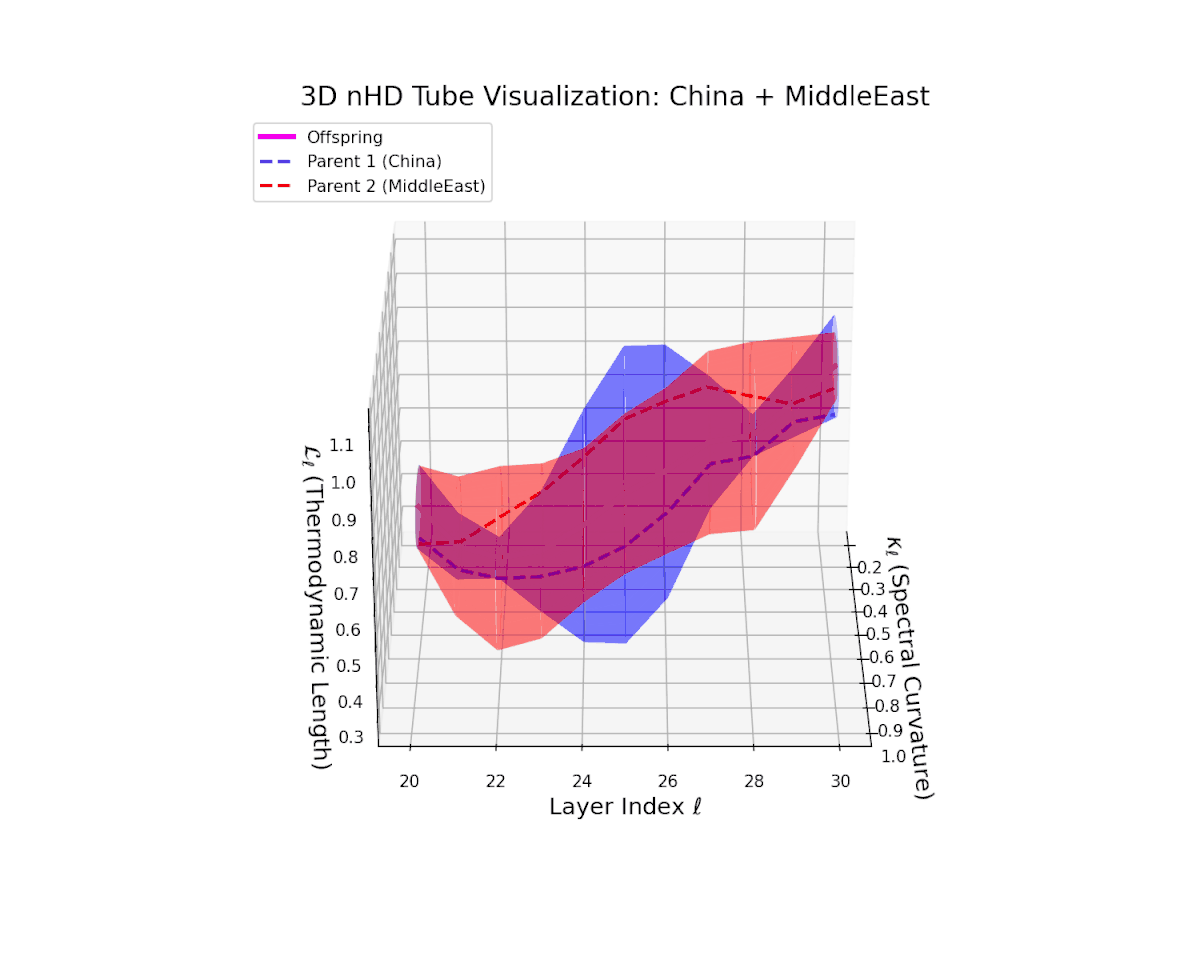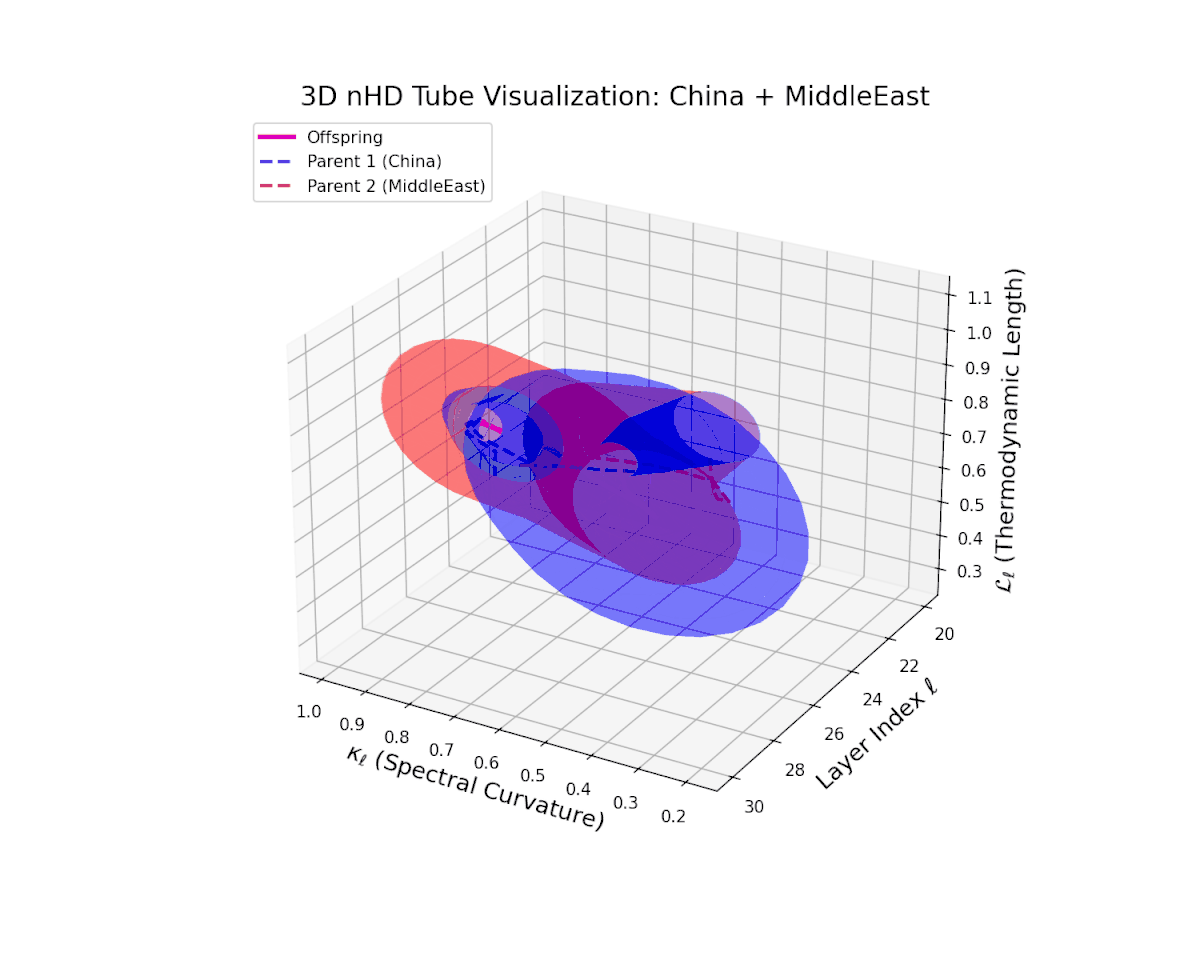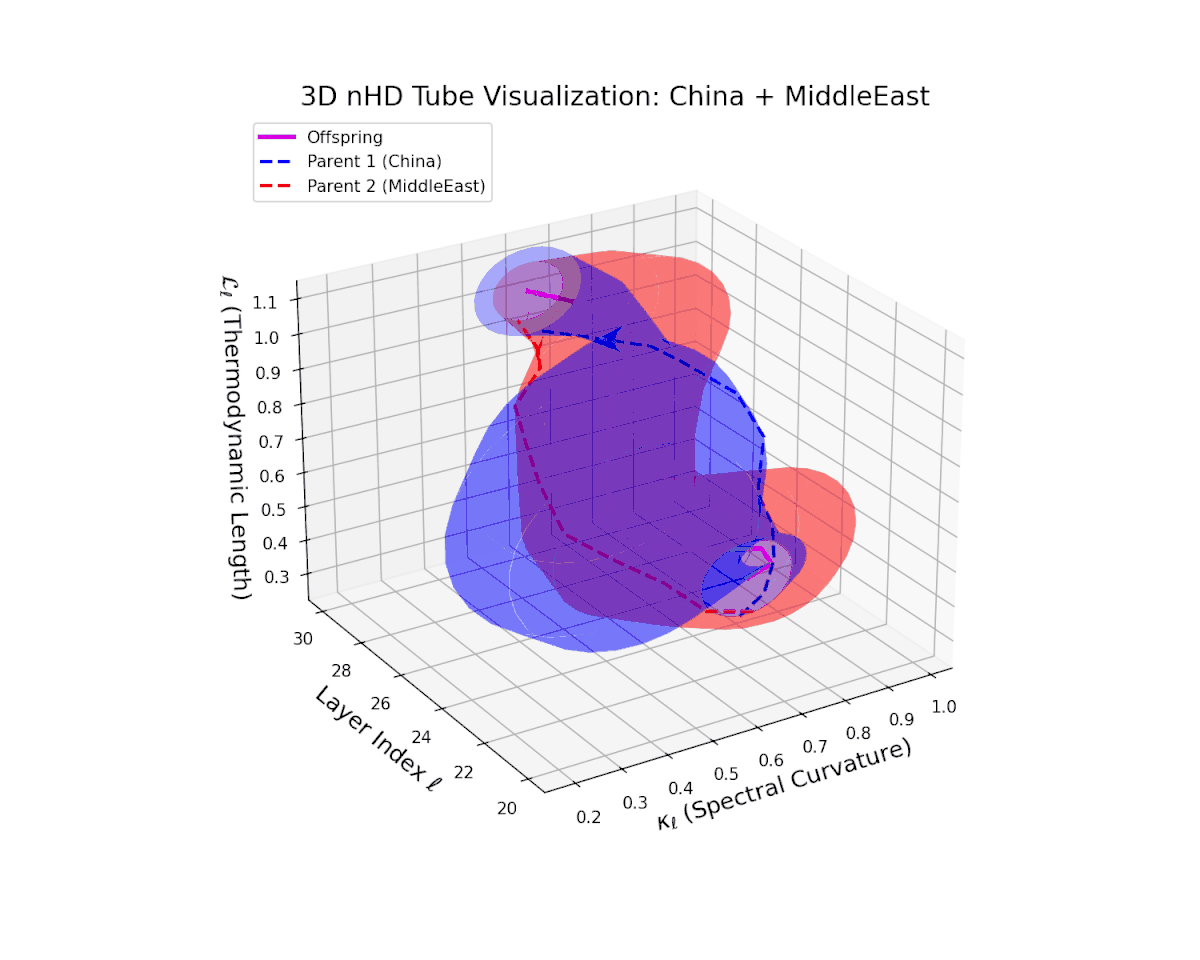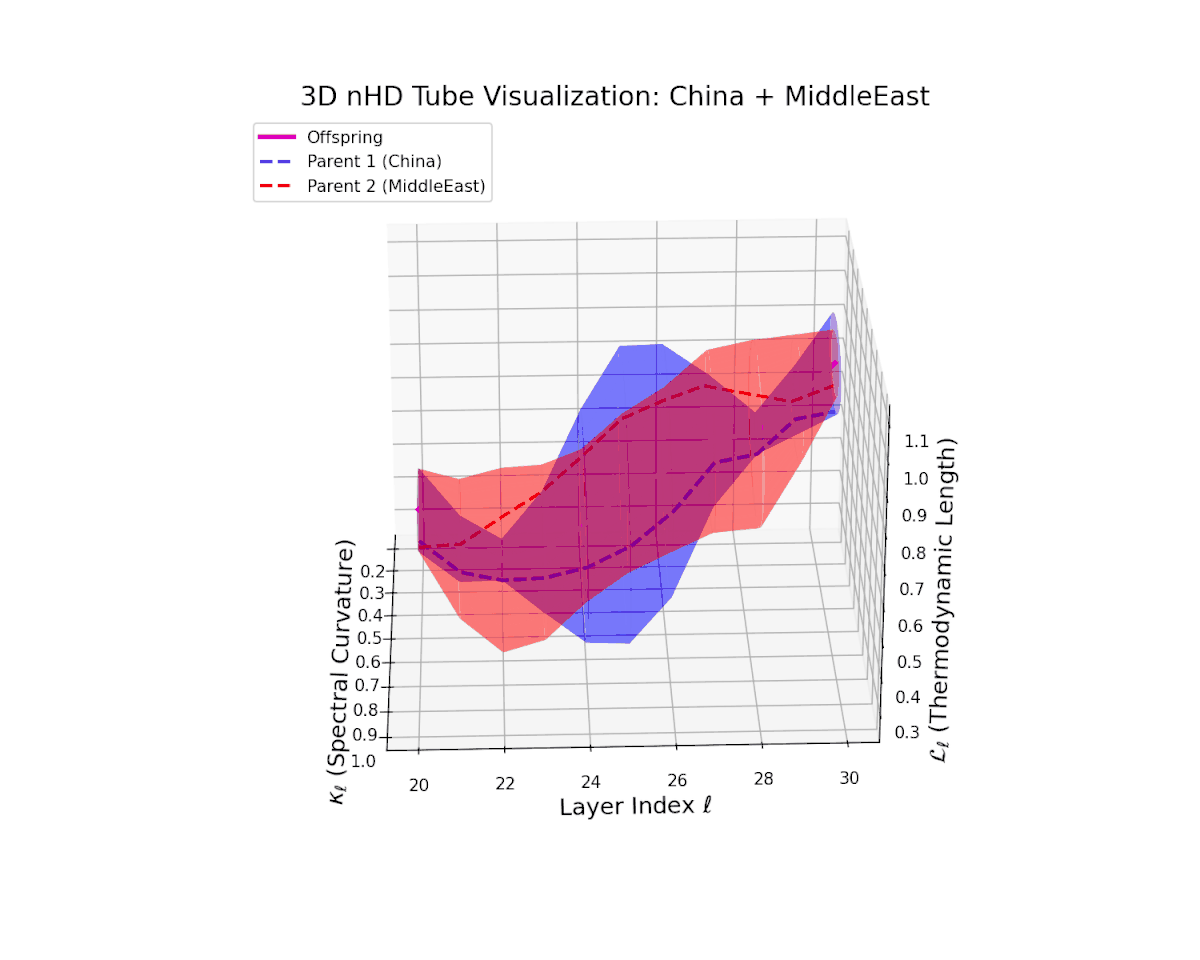
**(XII) China–Middle East Fusion**
Across transformer layers $\ell = 20$ to $30$, the offspring manifold (magenta) demonstrates a balanced and smooth interpolation of parental latent manifolds, with spectral curvature $\kappa_{\ell}$ increasing steadily from about $0.35$ to $0.85$. The thermodynamic length $L_{\ell}$ concurrently extends from $0.5$ to $1.0$, quantifying the accumulated Fisher-Rao semantic divergence. The continuous and gradual geometric transformation signals a stable semantic inheritance process, integrating culturally distinct representational features without abrupt topological distortions, thereby ensuring a coherent fusion of neural DNAs.

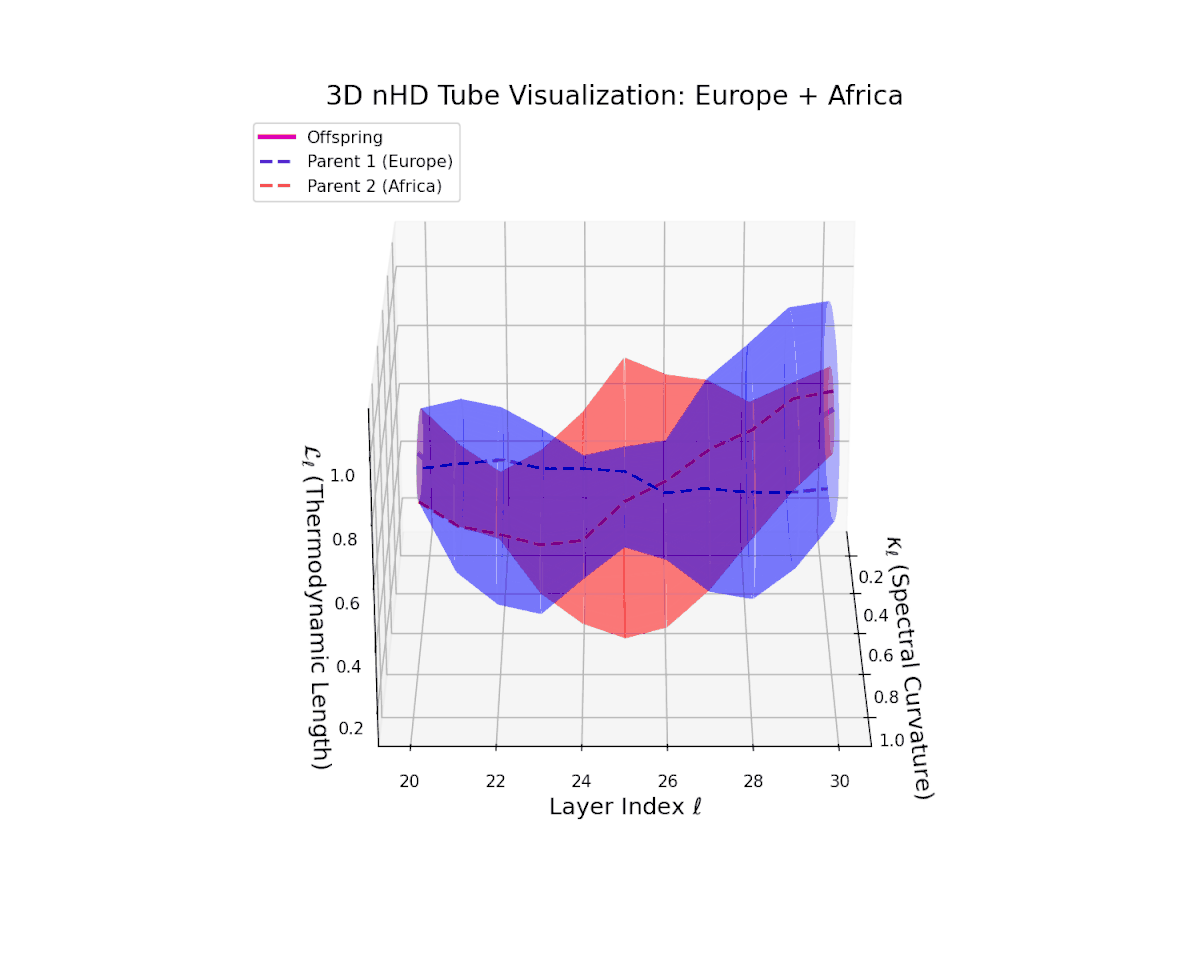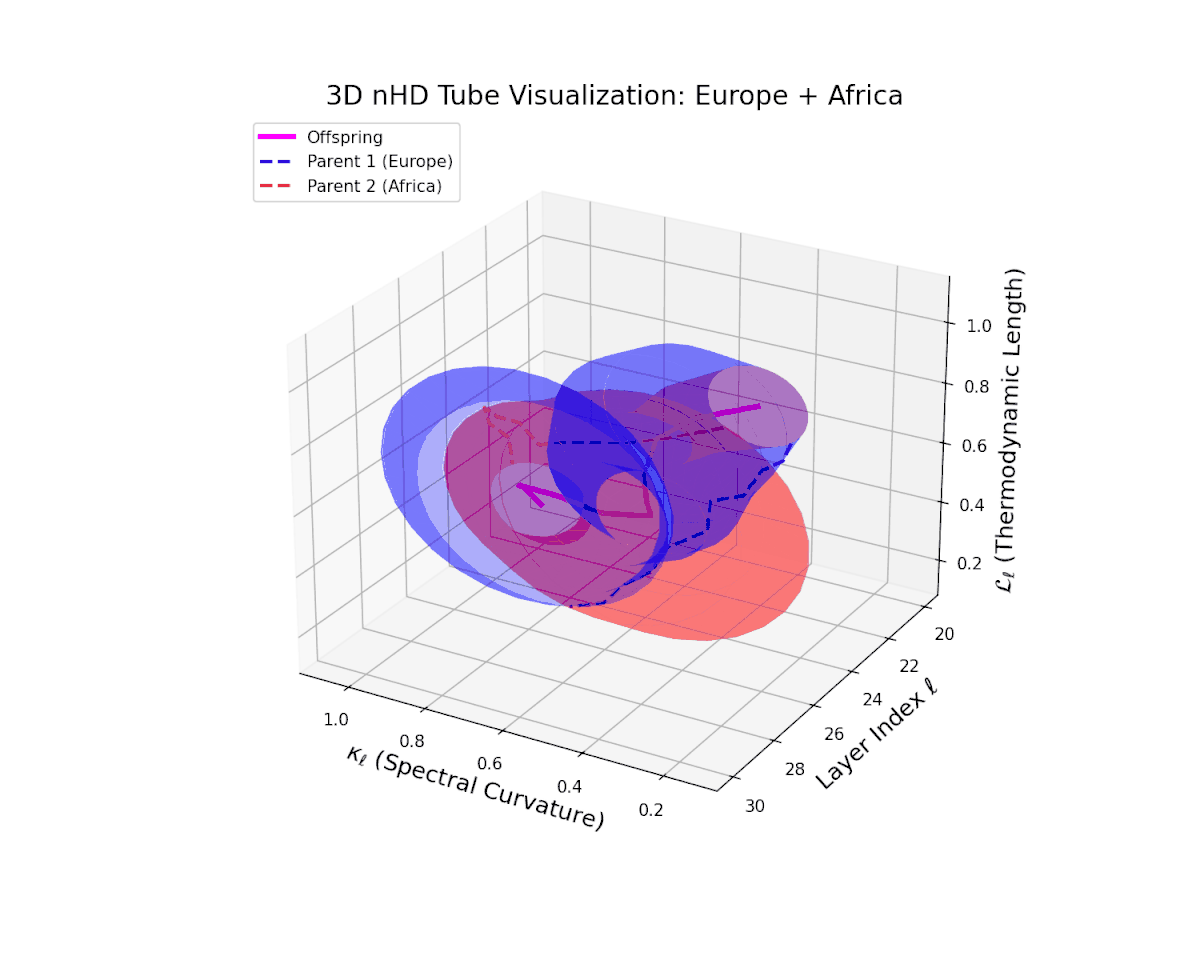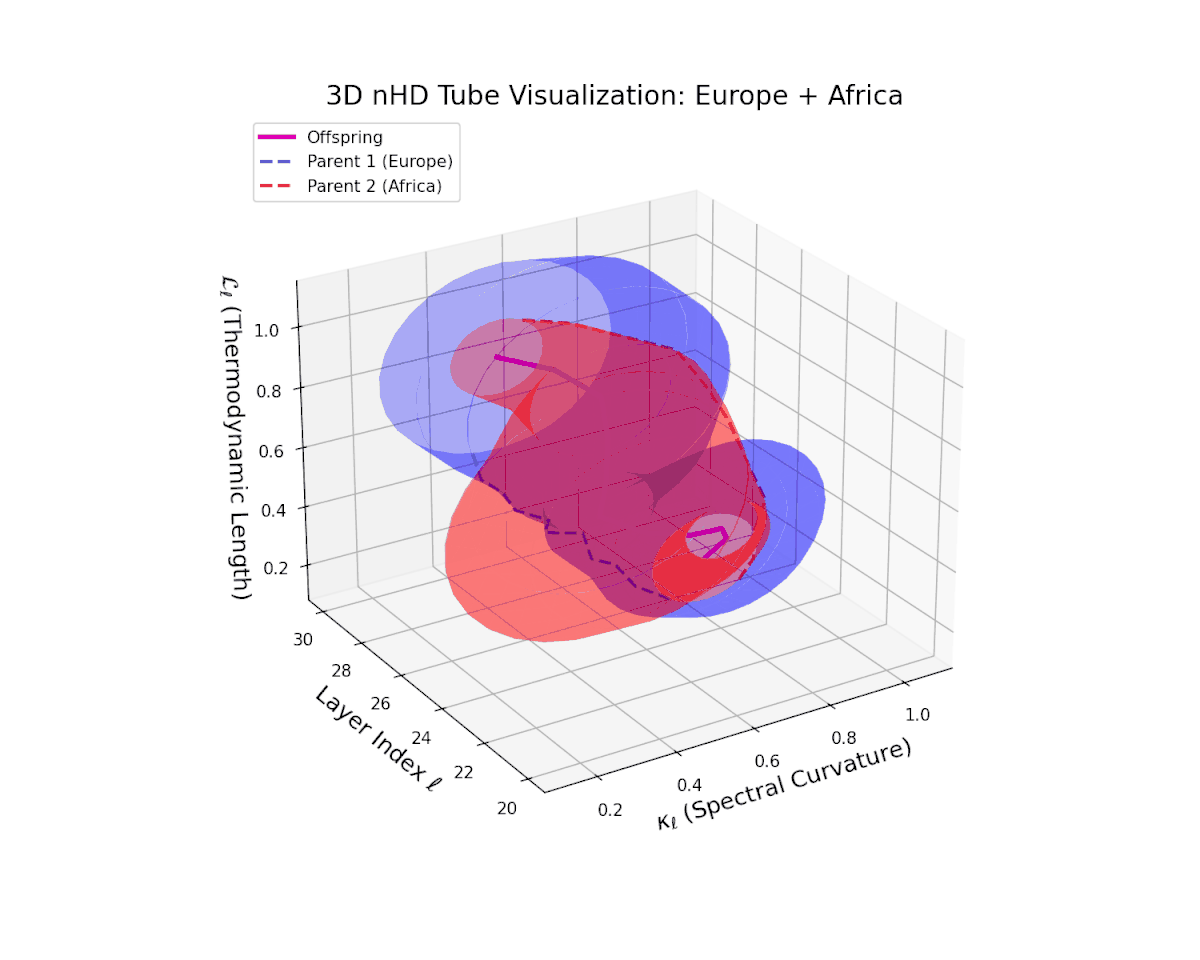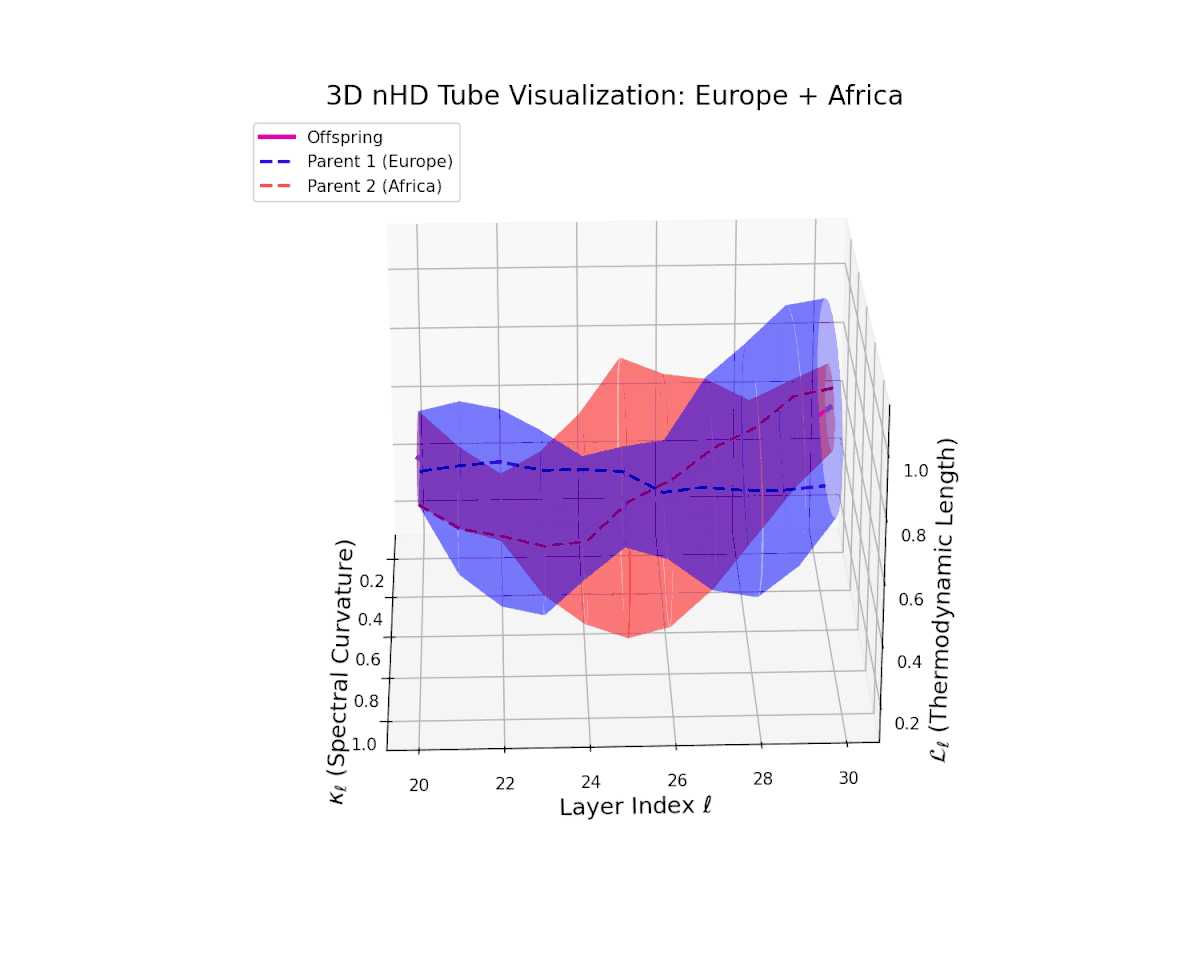
**(XIII) Europe–Africa Fusion**
The offspring latent manifold (magenta solid) continuously interpolates between parental manifolds (dashed blue and red), exhibiting spectral curvature $\kappa_{\ell}$ rising from $0.25$ to $0.7$. This monotonic increase reflects growing local latent complexity and enhanced nonlinear feature interactions across layers $\ell = 20$ to $30$. Concurrently, the thermodynamic length $L_{\ell}$ spans $0.4$ to $0.85$, capturing the accumulated Fisher-Rao information distance traversed by semantic representations. This smooth geometric evolution underscores effective integration of culturally diverse semantic priors, yielding a robust latent manifold embodying nuanced semantic inheritance.

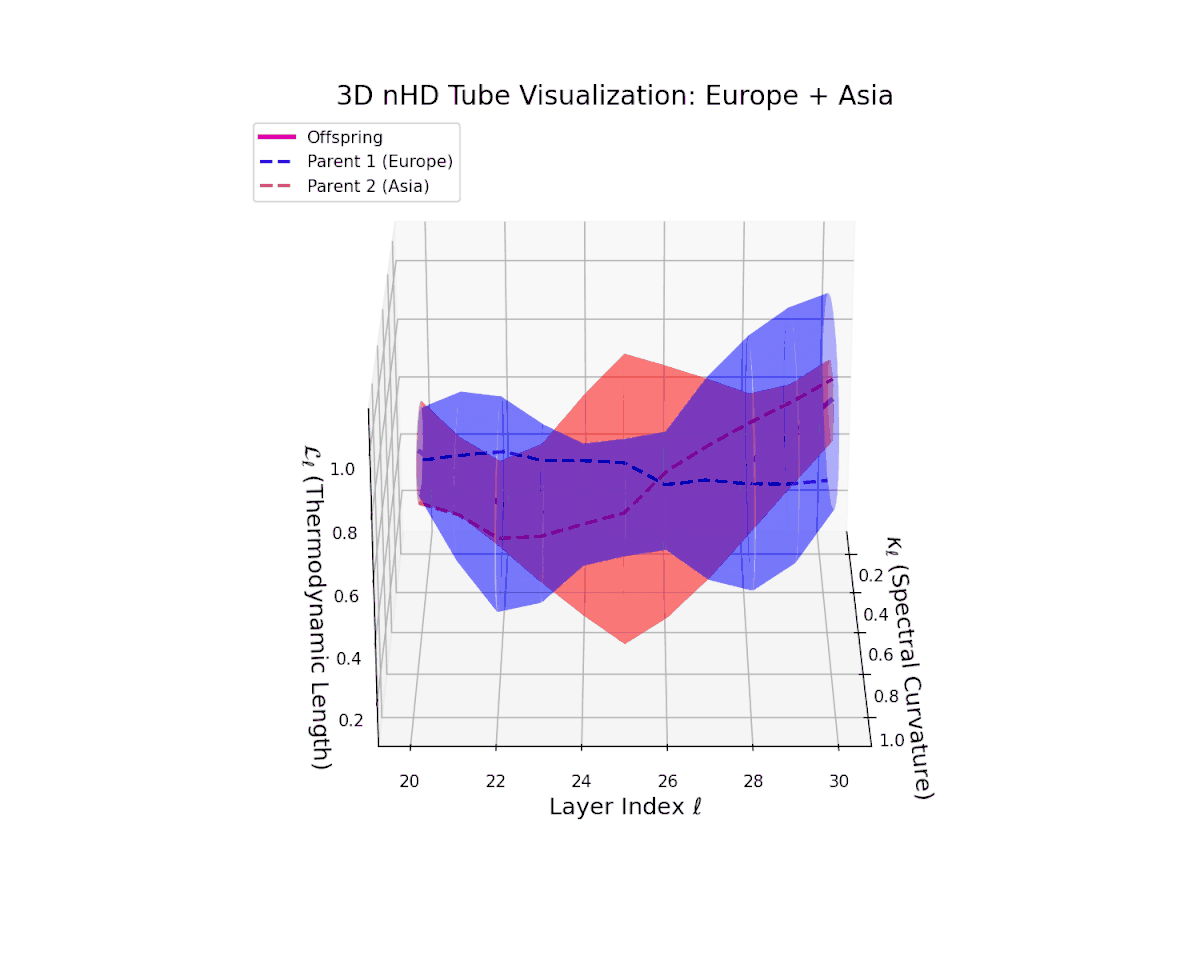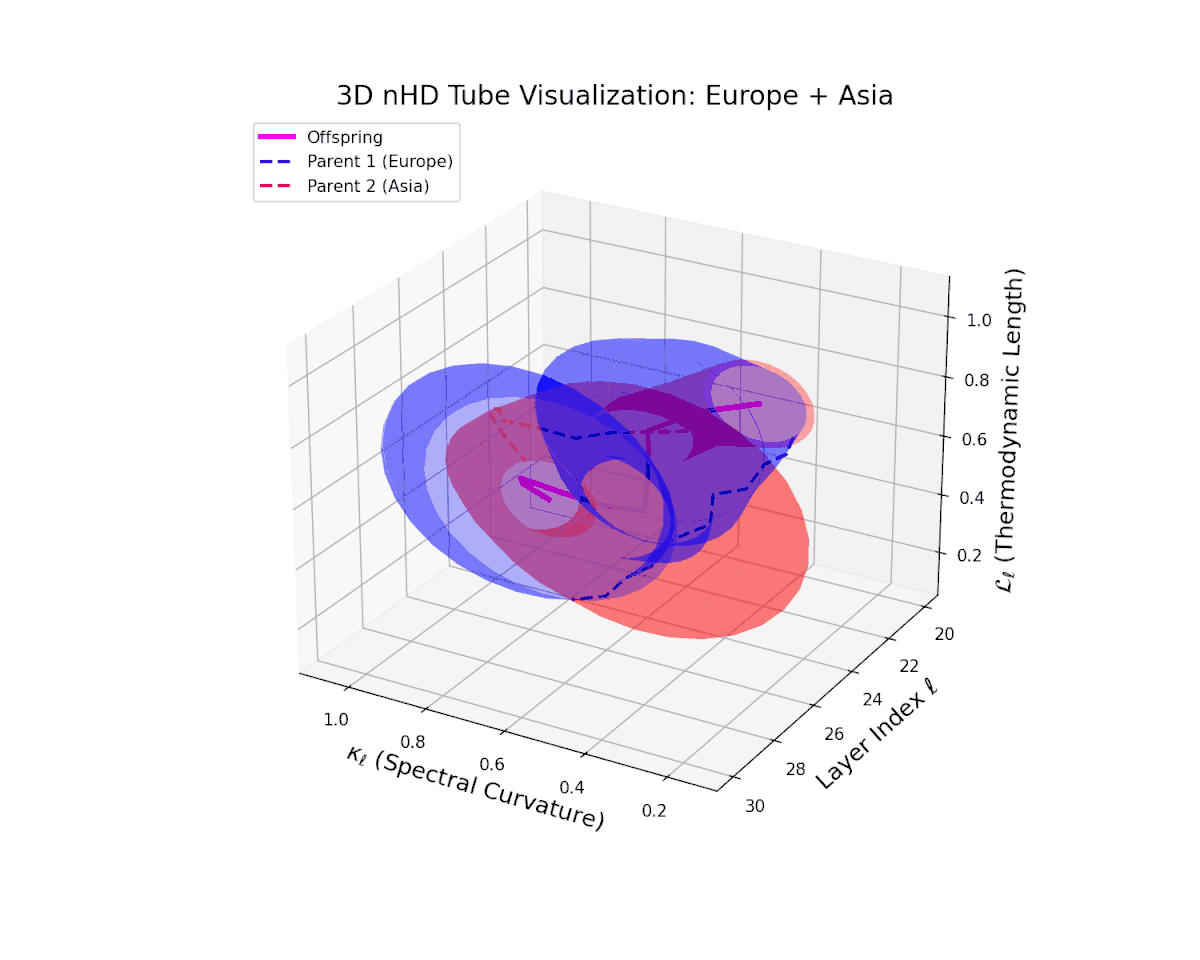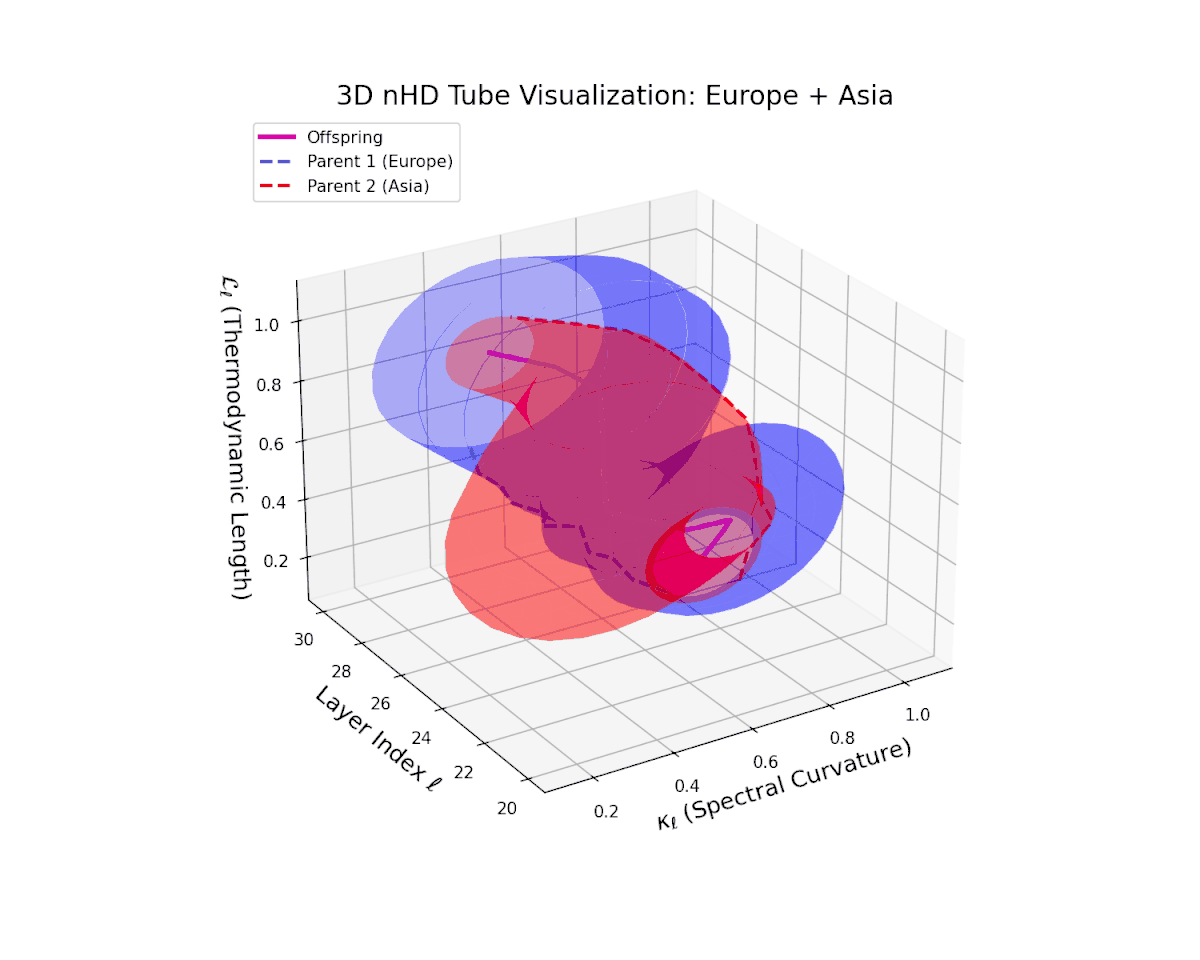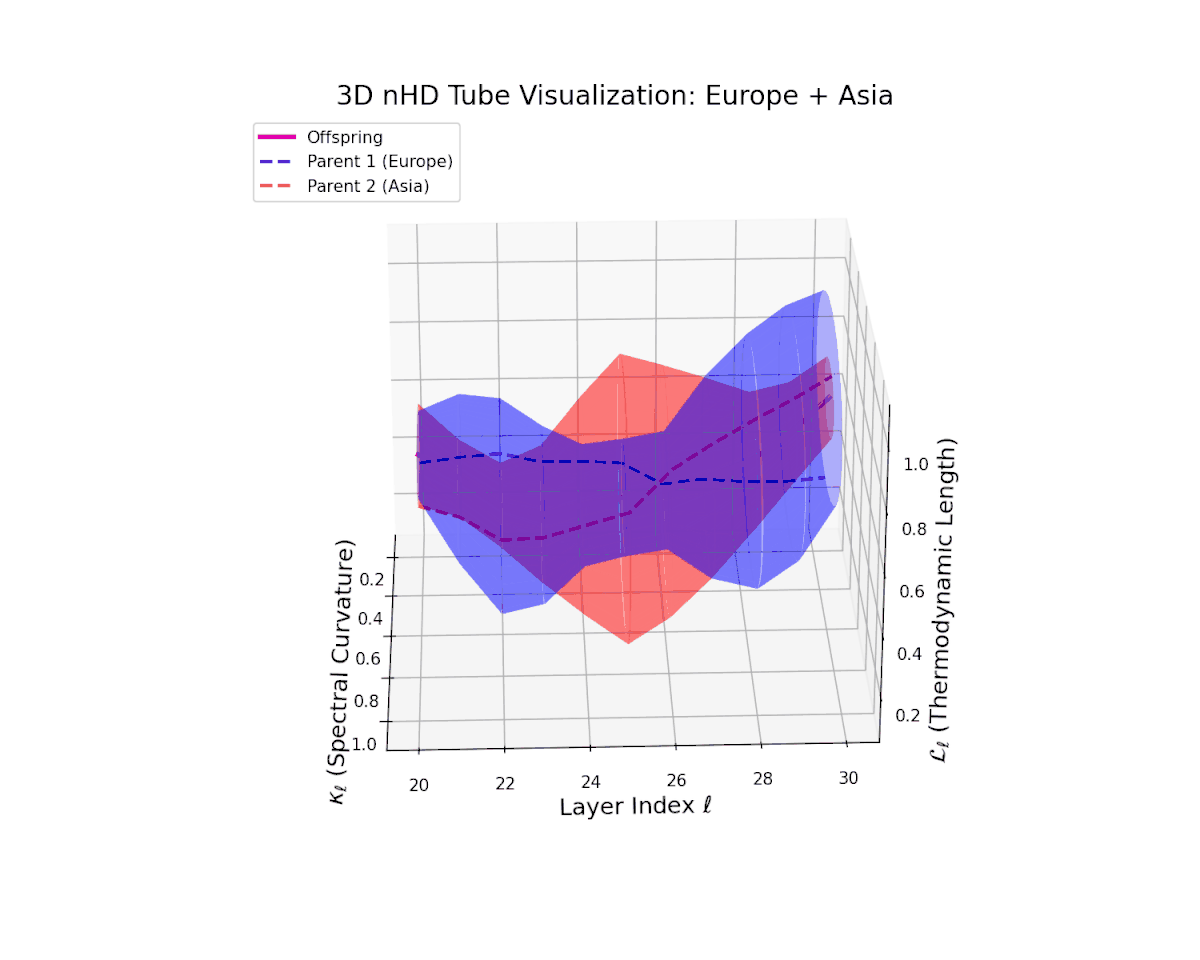
**(XIV) Europe–Asia Fusion**
The offspring manifold tightly occupies the convex latent space framed by parent manifolds, with spectral curvature $\kappa_{\ell}$ progressing from $0.3$ to $0.75$, signaling increased manifold bending and representational intricacy. Simultaneously, thermodynamic length $L_{\ell}$ increases from $0.45$ to $0.9$, reflecting cumulative semantic transformation via the Fisher-Rao metric. This smooth, layered evolution mirrors hierarchical compositionality and geometric deformation, revealing a richly structured fusion of cultural neural DNAs across deep transformer layers.

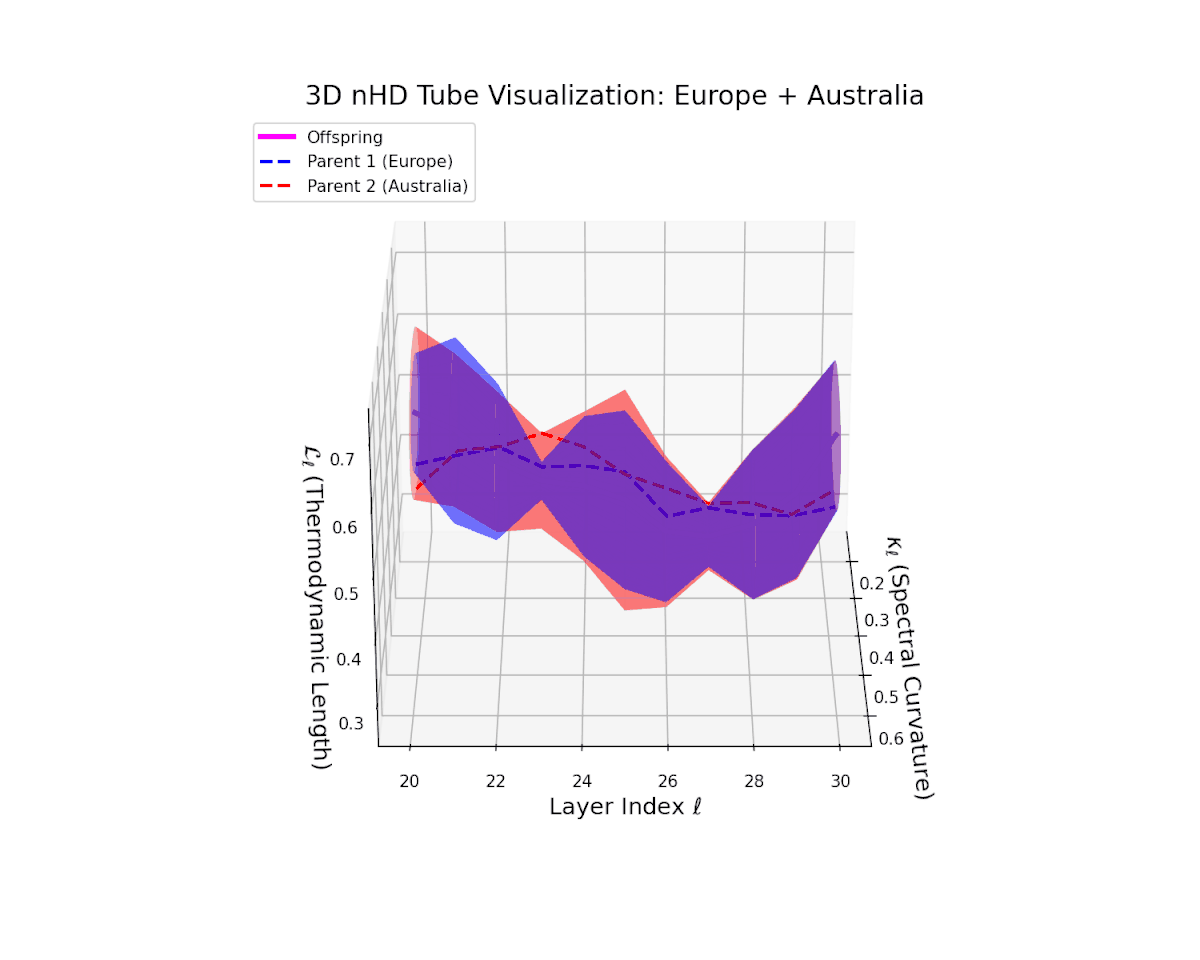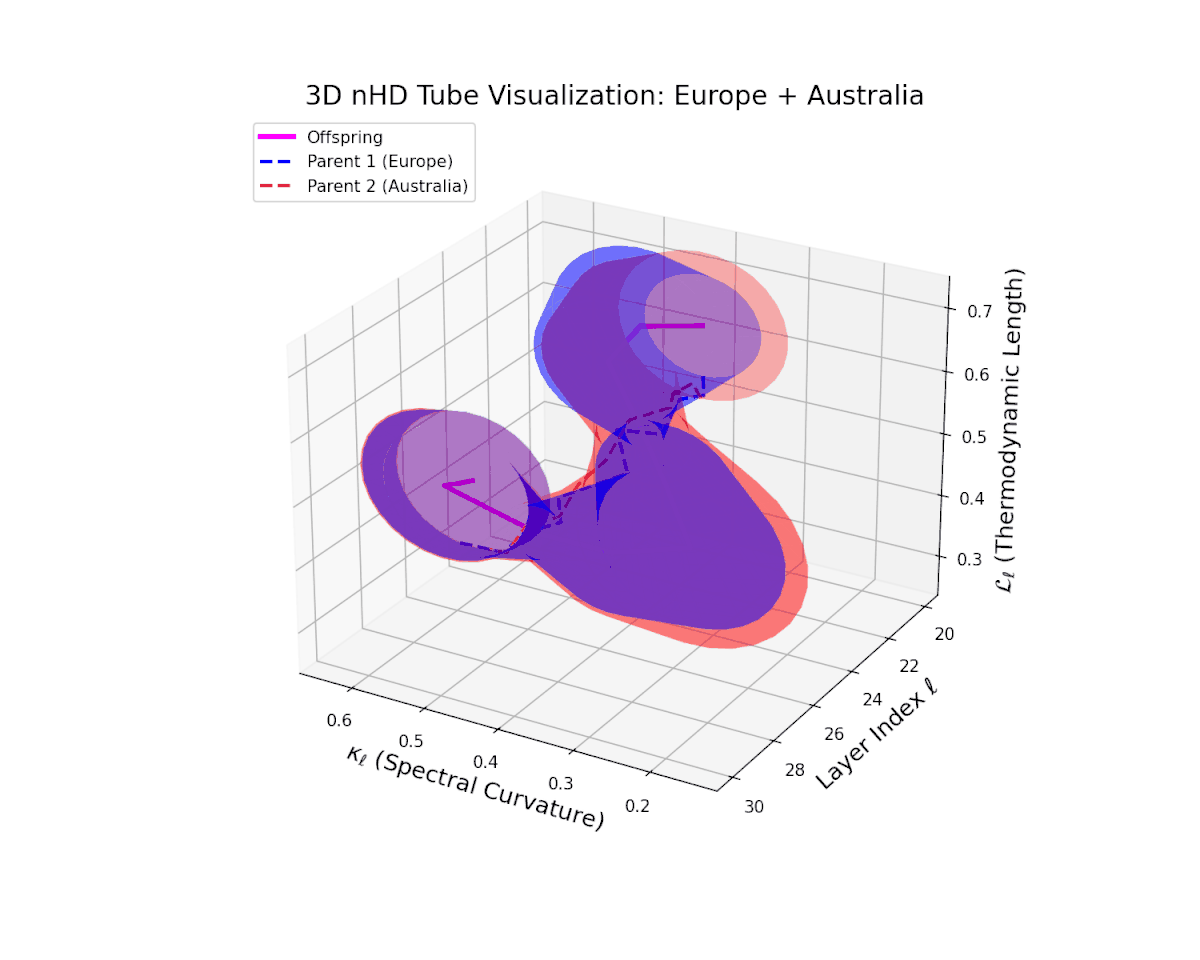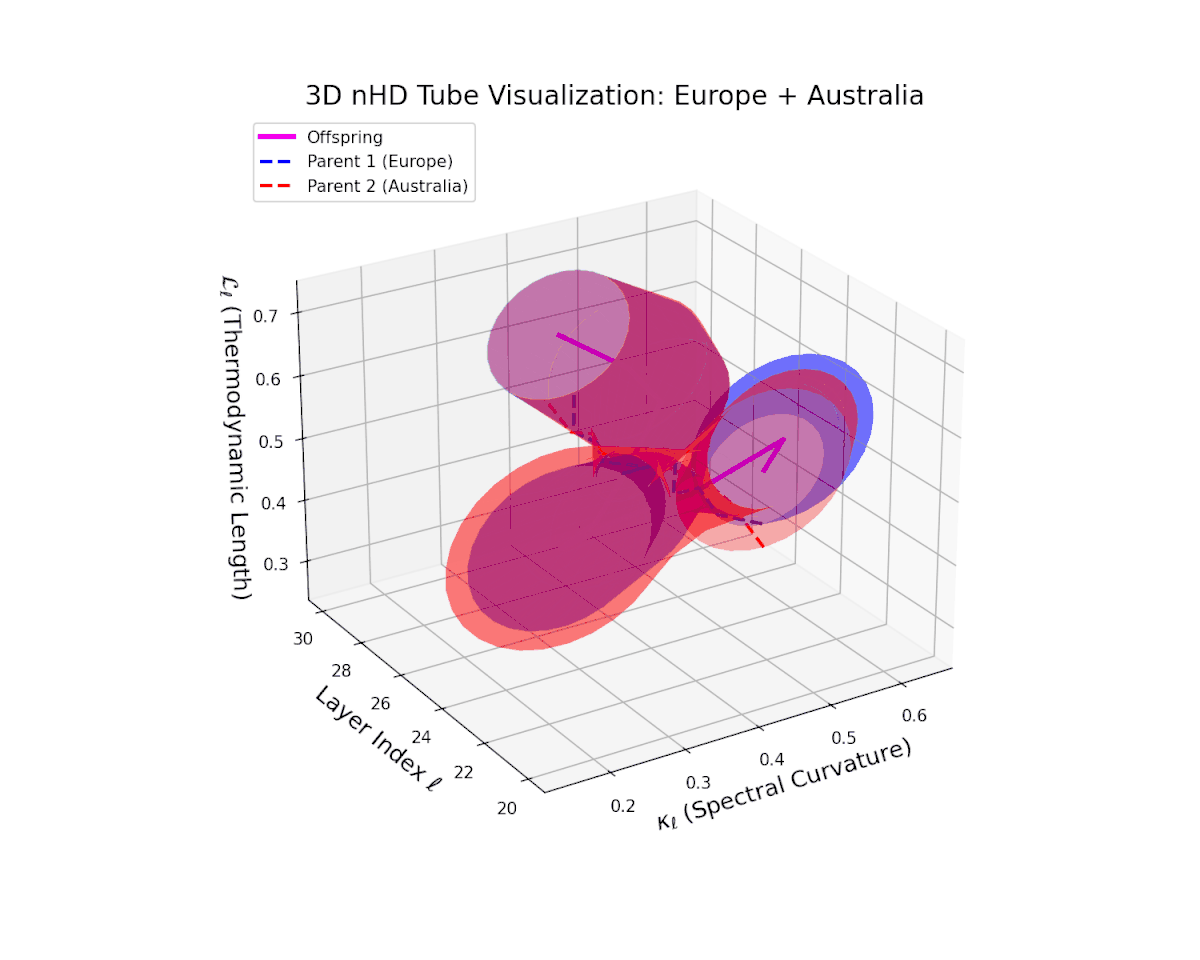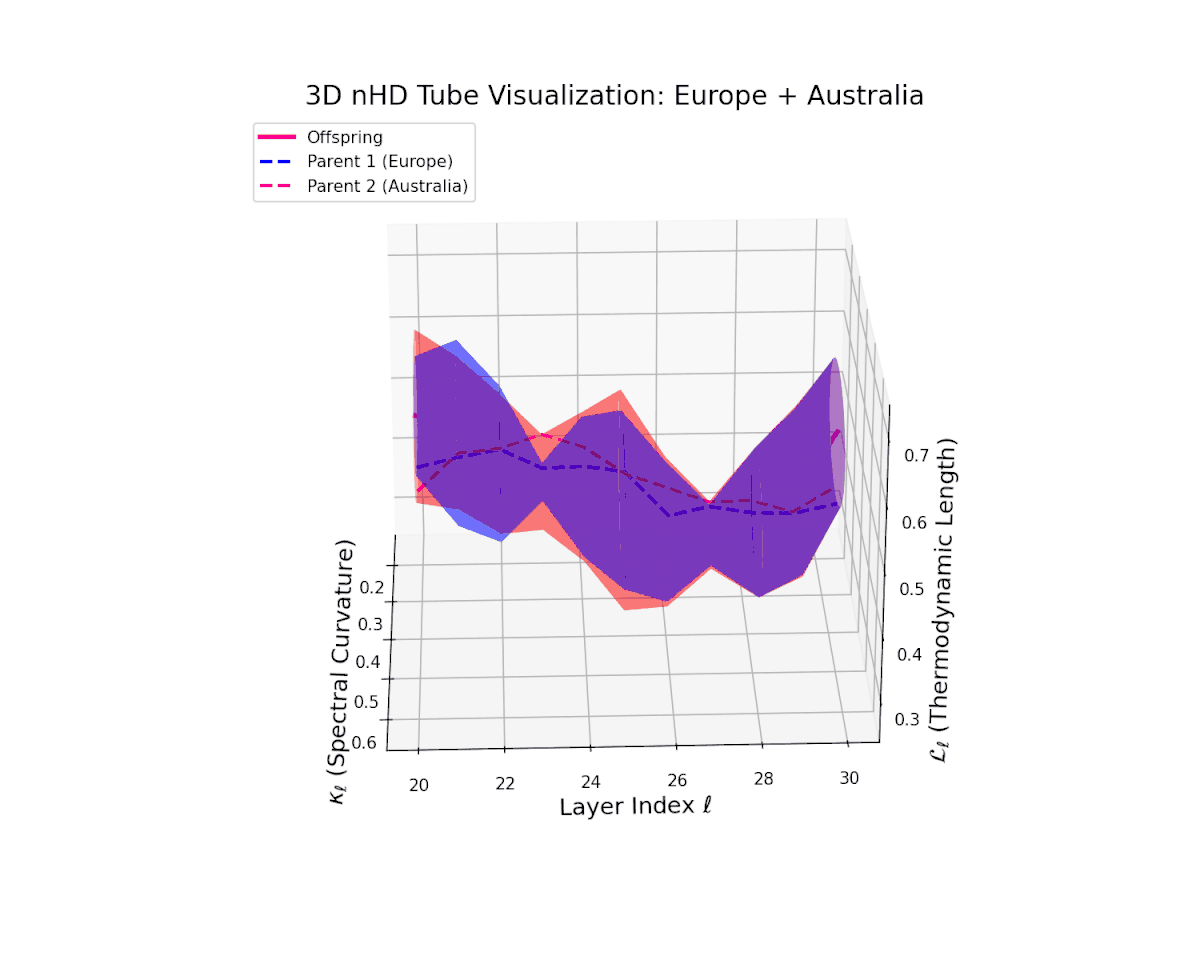
**(XV) Europe–Australia Fusion**
The offspring manifold manifests a continuous geodesic between parental latent spaces, with spectral curvature $\kappa_{\ell}$ smoothly ascending from approximately $0.3$ to $0.7$. The thermodynamic length $L_{\ell}$ concurrently increases from $0.4$ to $0.85$, indicating progressive accumulation of semantic representational change. This geometric stability across layers highlights the preservation and harmonious fusion of diverse cultural semantic priors within the latent space.

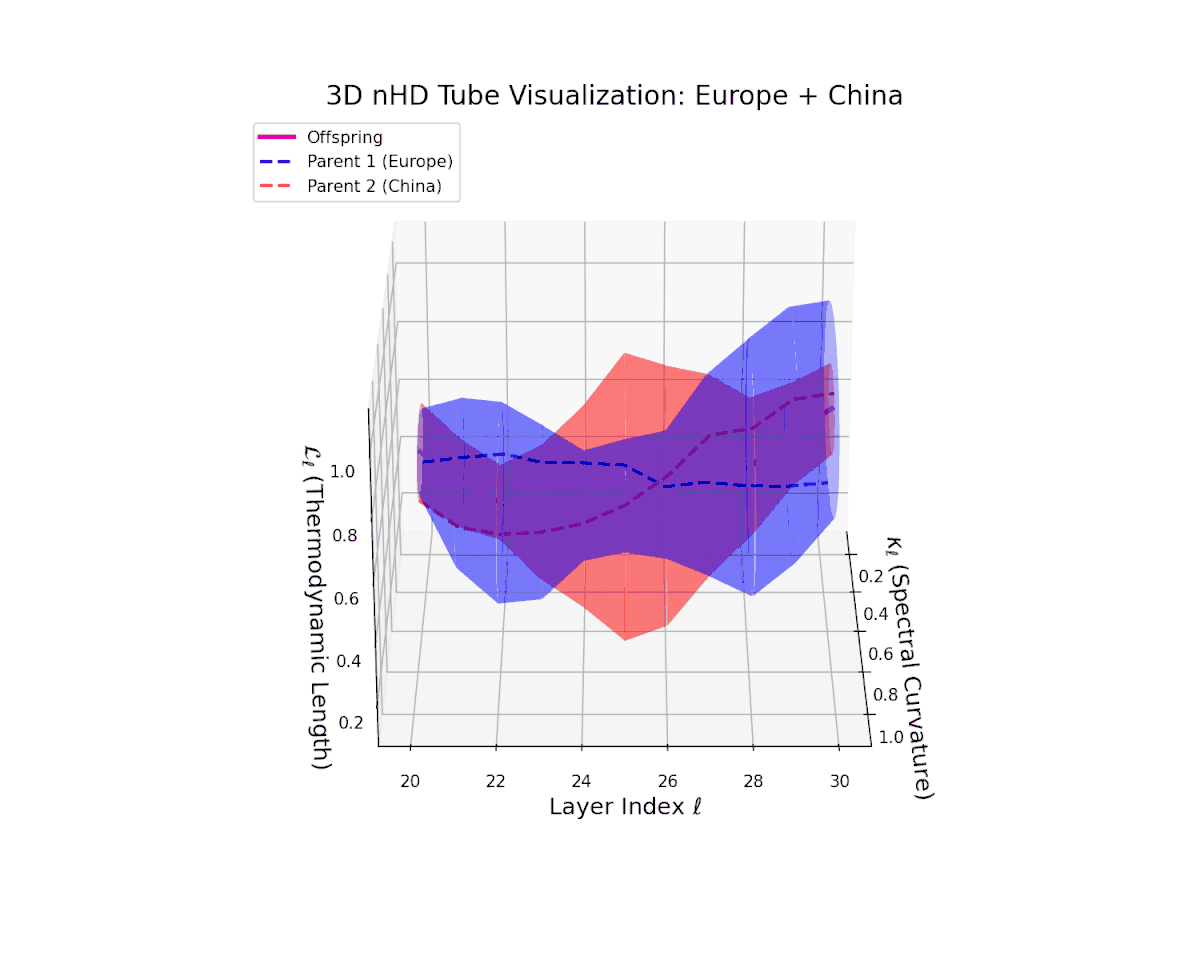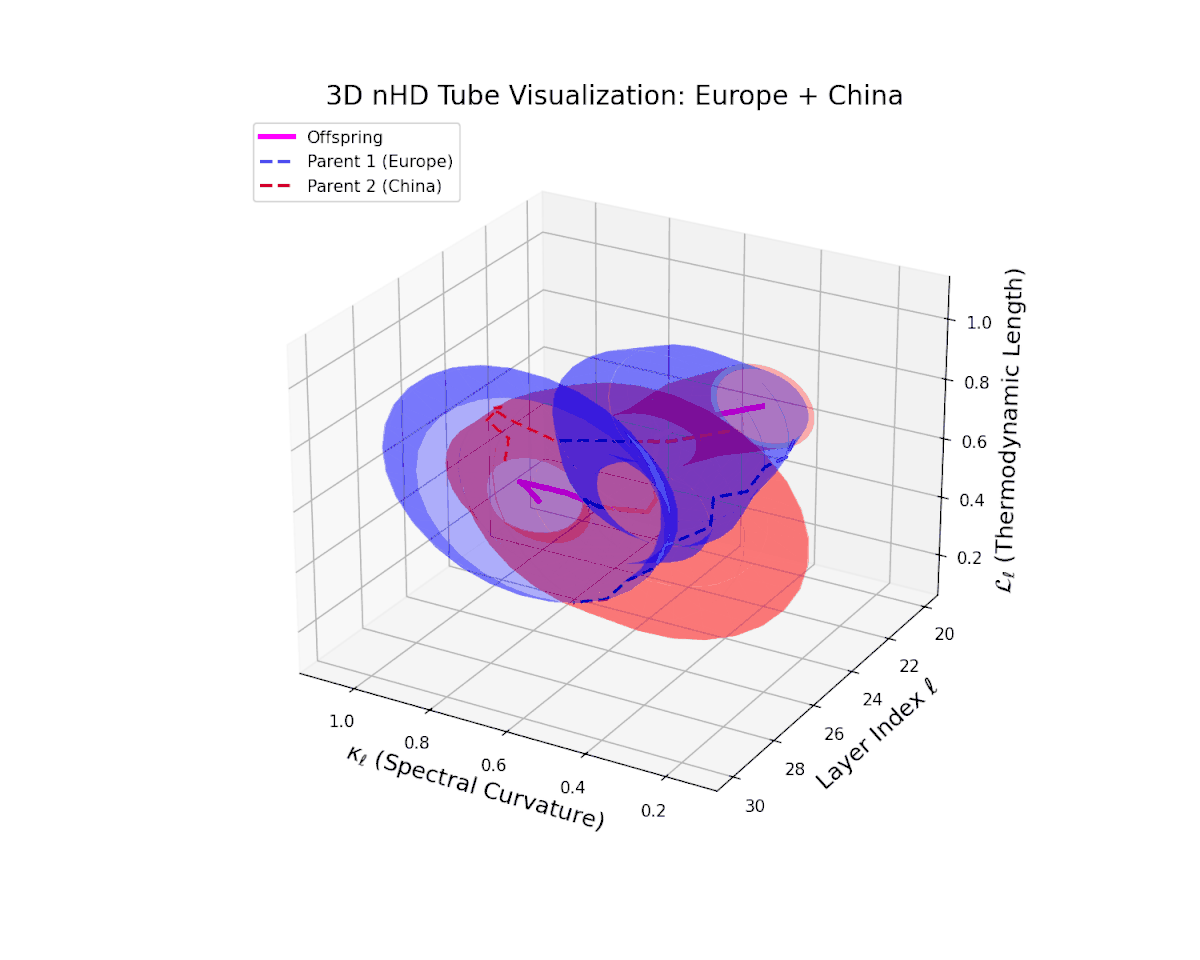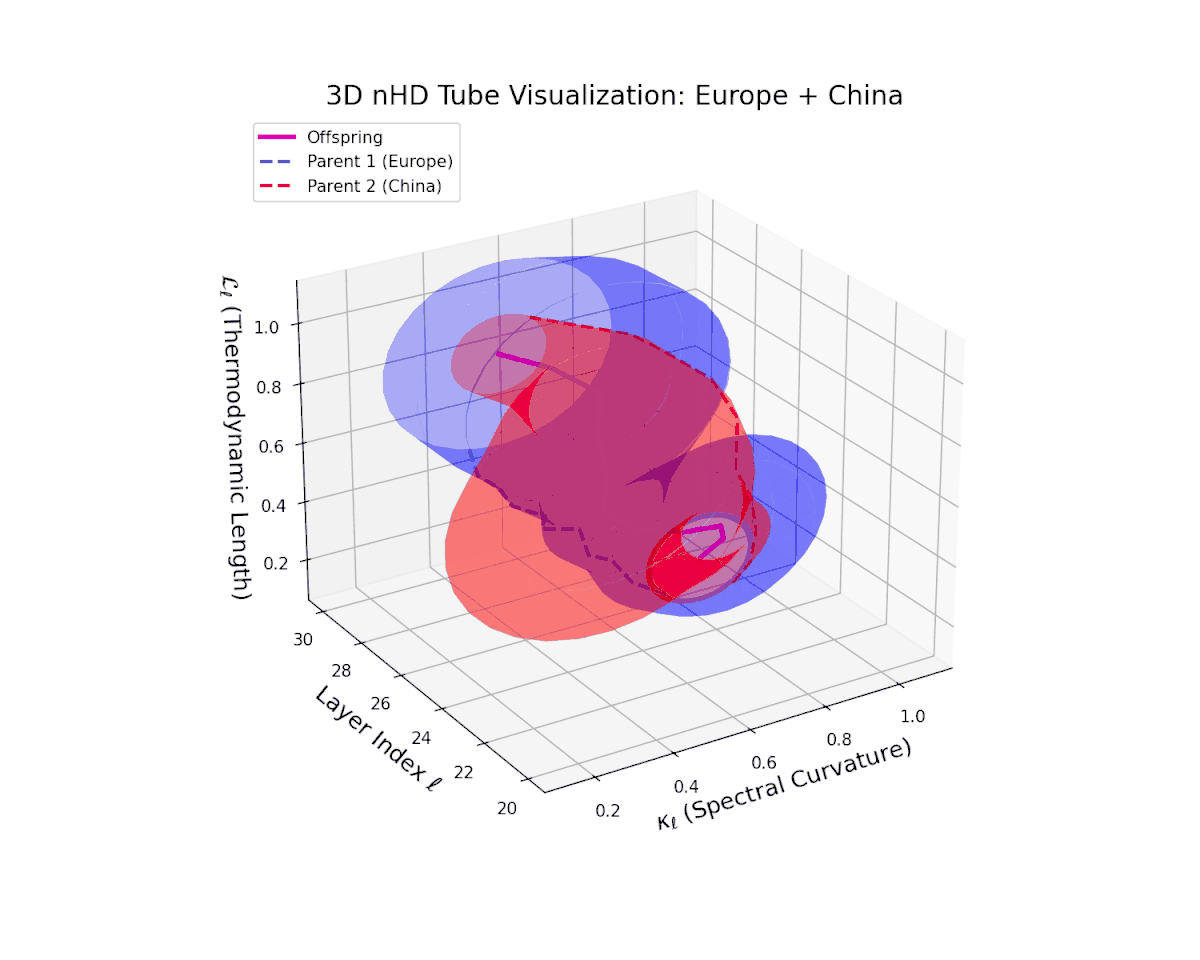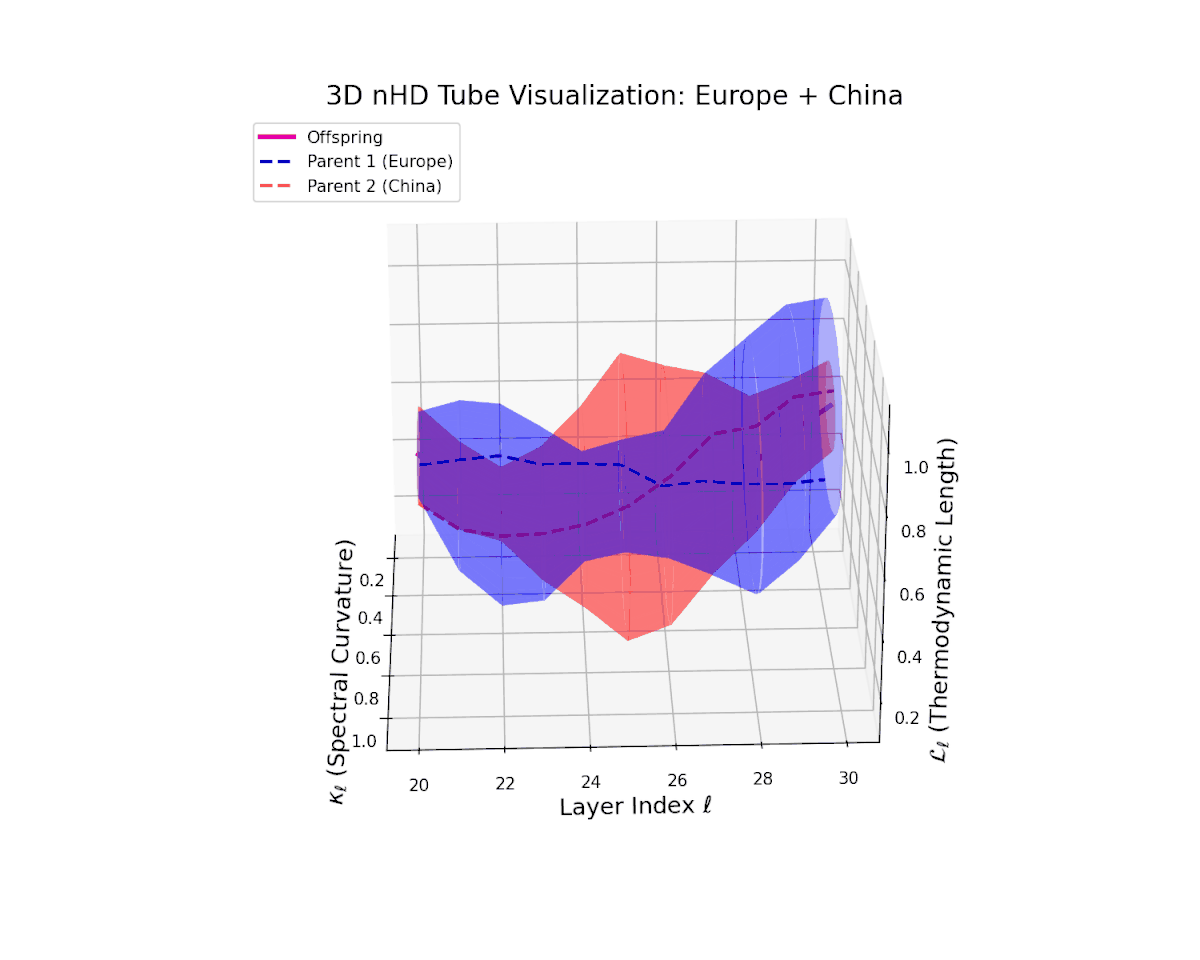
**(XVI) Europe–China Fusion**
The offspring latent manifold (magenta) displays spectral curvature $\kappa_{\ell}$ increasing steadily from $0.35$ to $0.8$, signaling escalating nonlinear representational complexity. The thermodynamic length $L_{\ell}$ extends from $0.5$ to $0.95$, capturing accumulated semantic change. This dynamic reshaping reflects a robust and nuanced semantic fusion of distinct cultural neural DNAs, evidencing gradual compositional innovation within deep model layers.

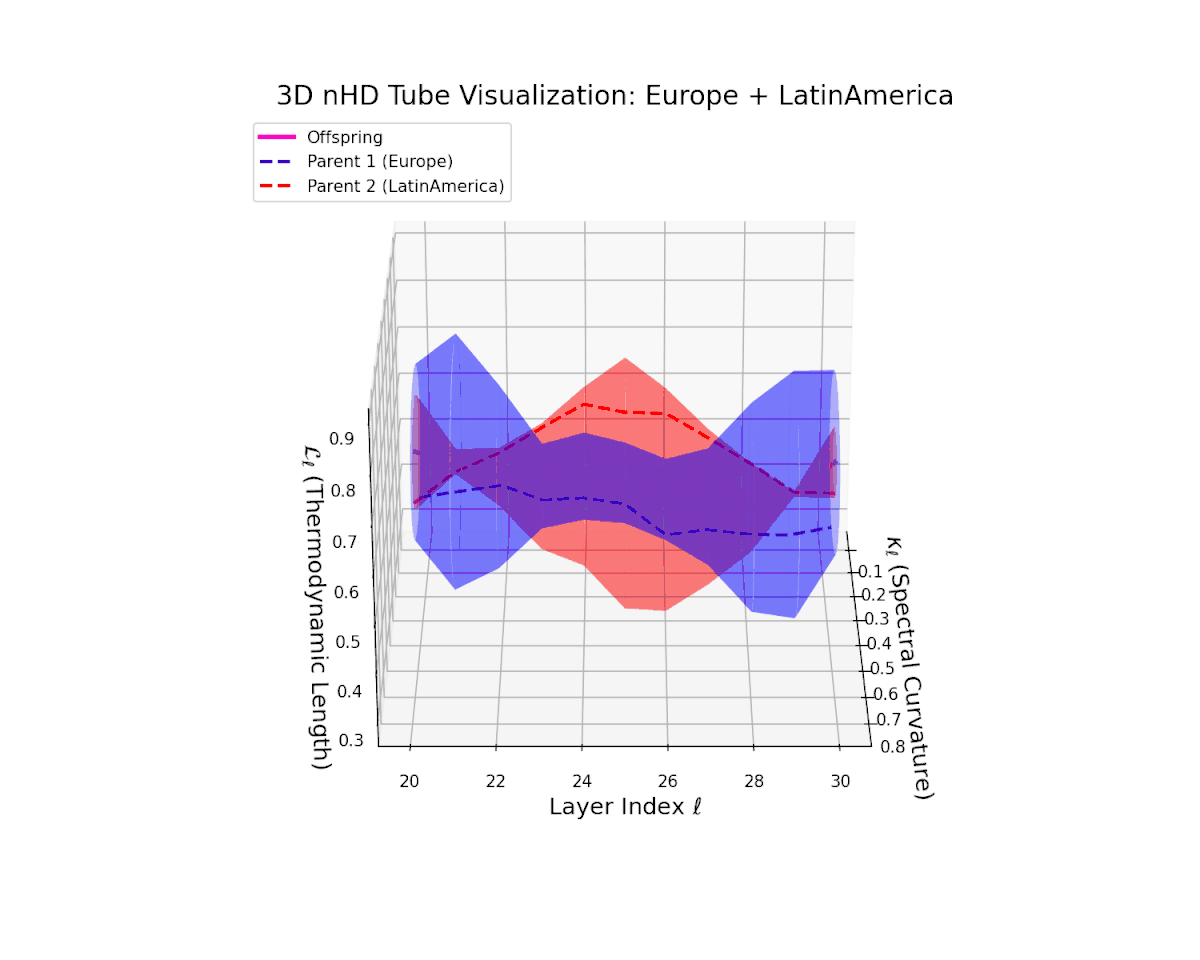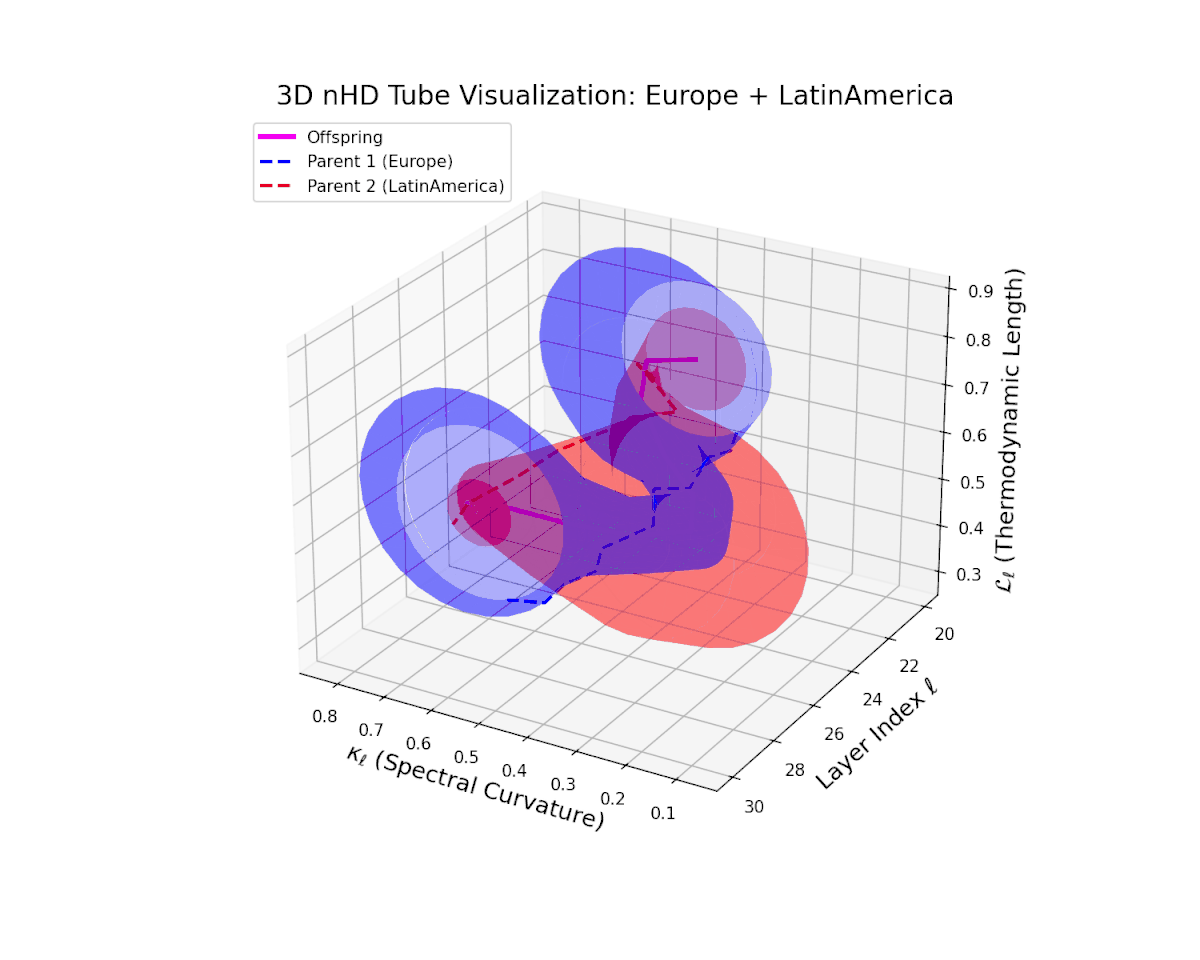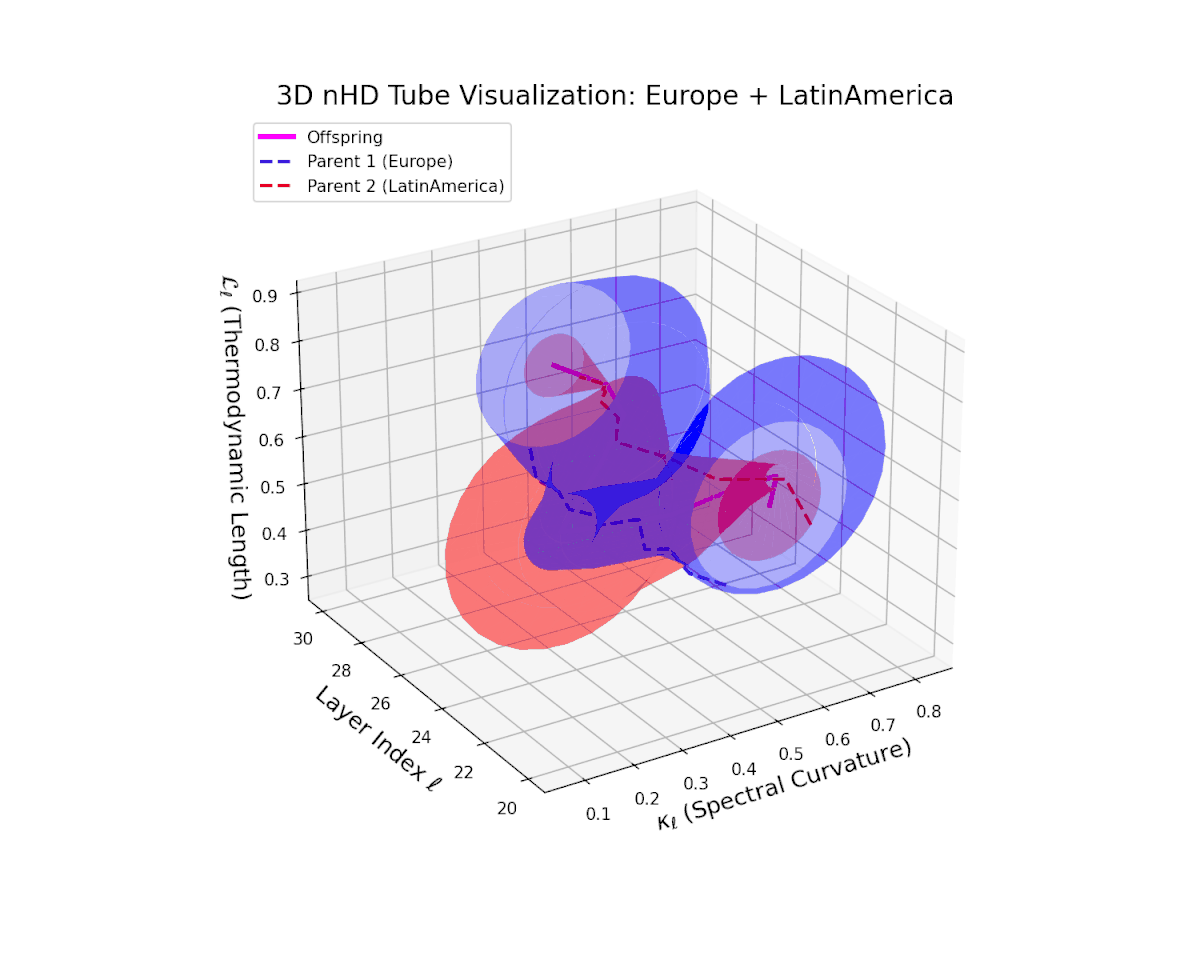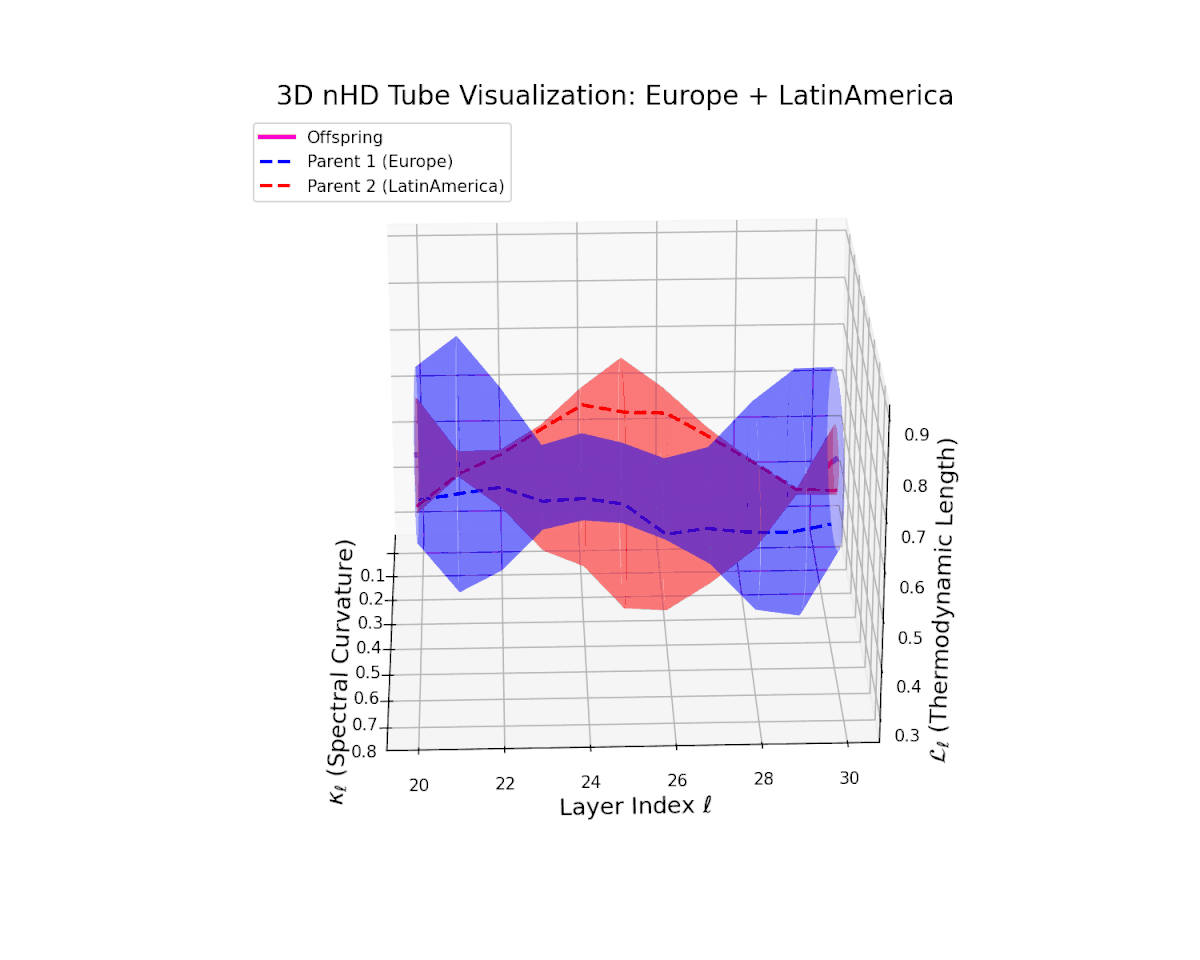
**(XVII) Europe–Latin America Fusion**
The offspring manifold demonstrates a smooth increase in spectral curvature $\kappa_{\ell}$ from approximately $0.3$ to $0.75$, reflecting progressively richer local nonlinear geometric structure. Concurrently, the thermodynamic length $L_{\ell}$ expands from $0.45$ to $0.9$, marking extended cumulative semantic changes along the Fisher-Rao metric geodesic. These trends highlight a gradual semantic integration and evolving latent representational complexity, indicative of stable fusion across diverse cultural neural DNAs.

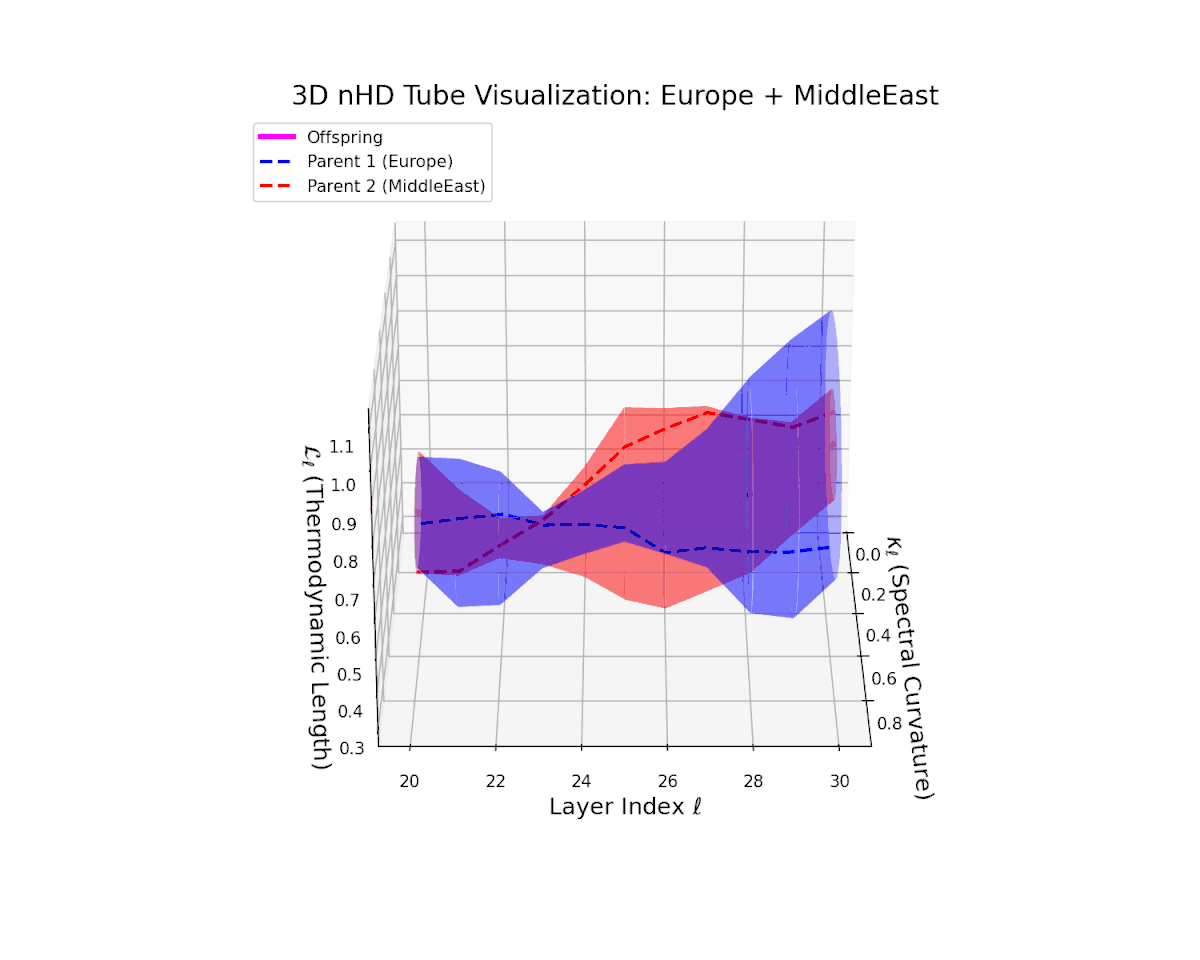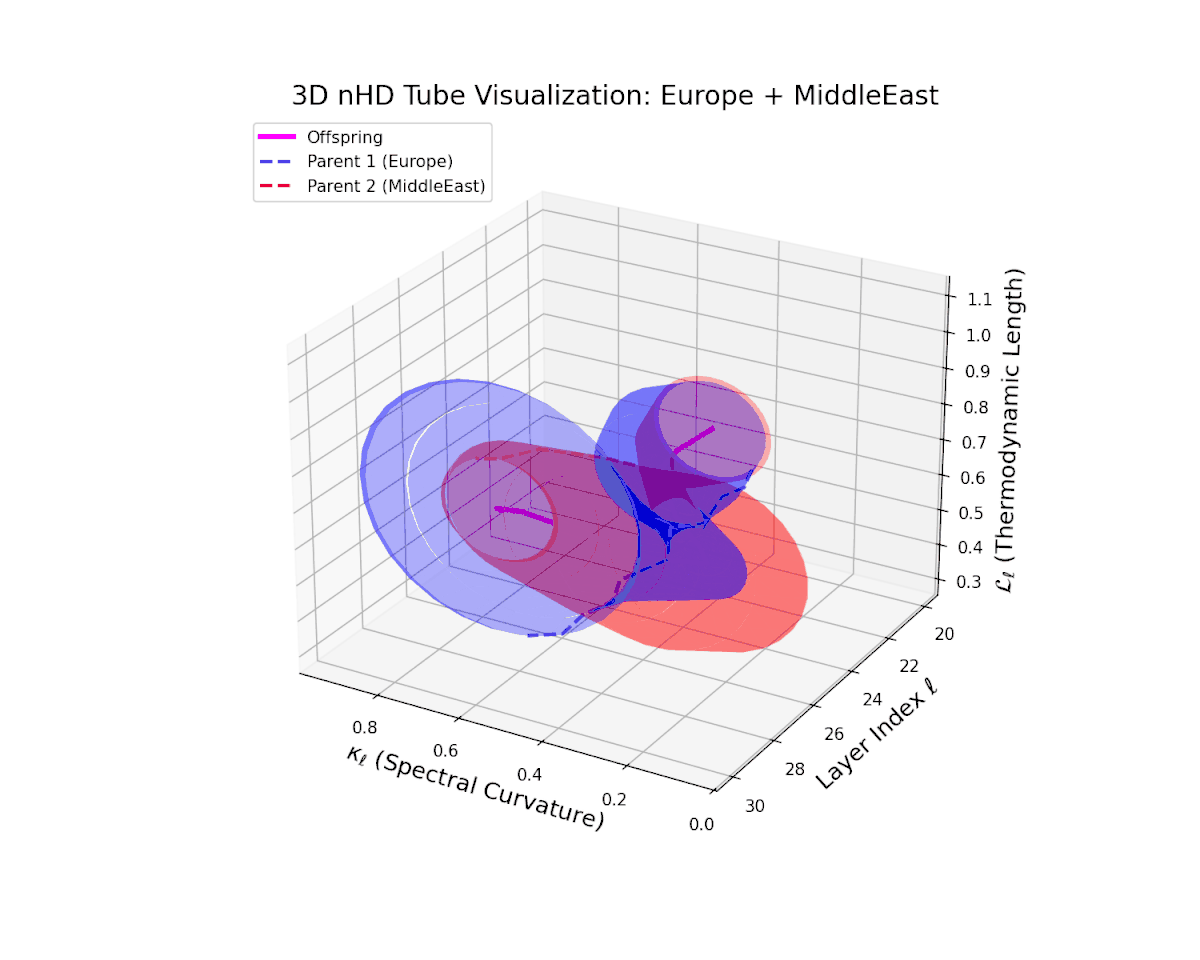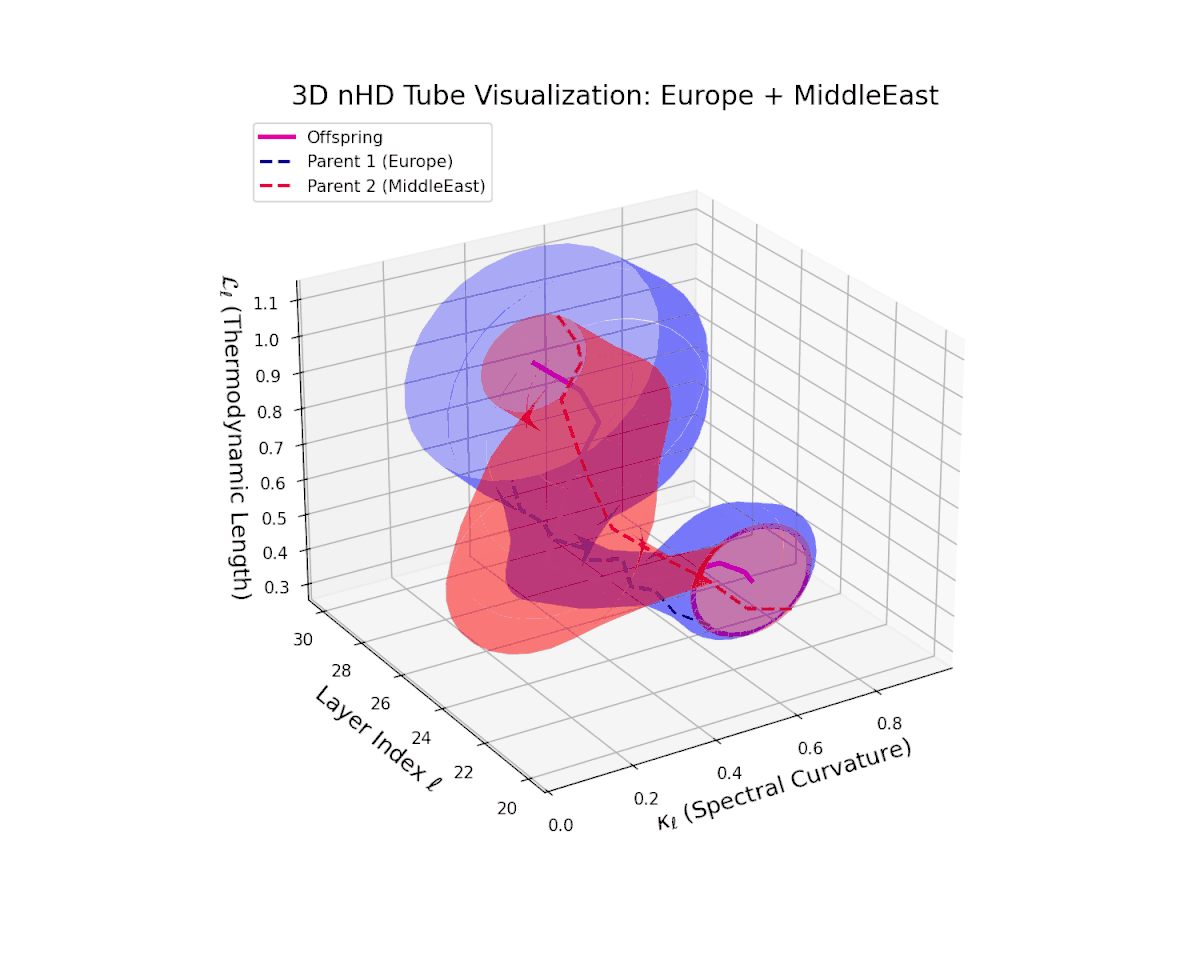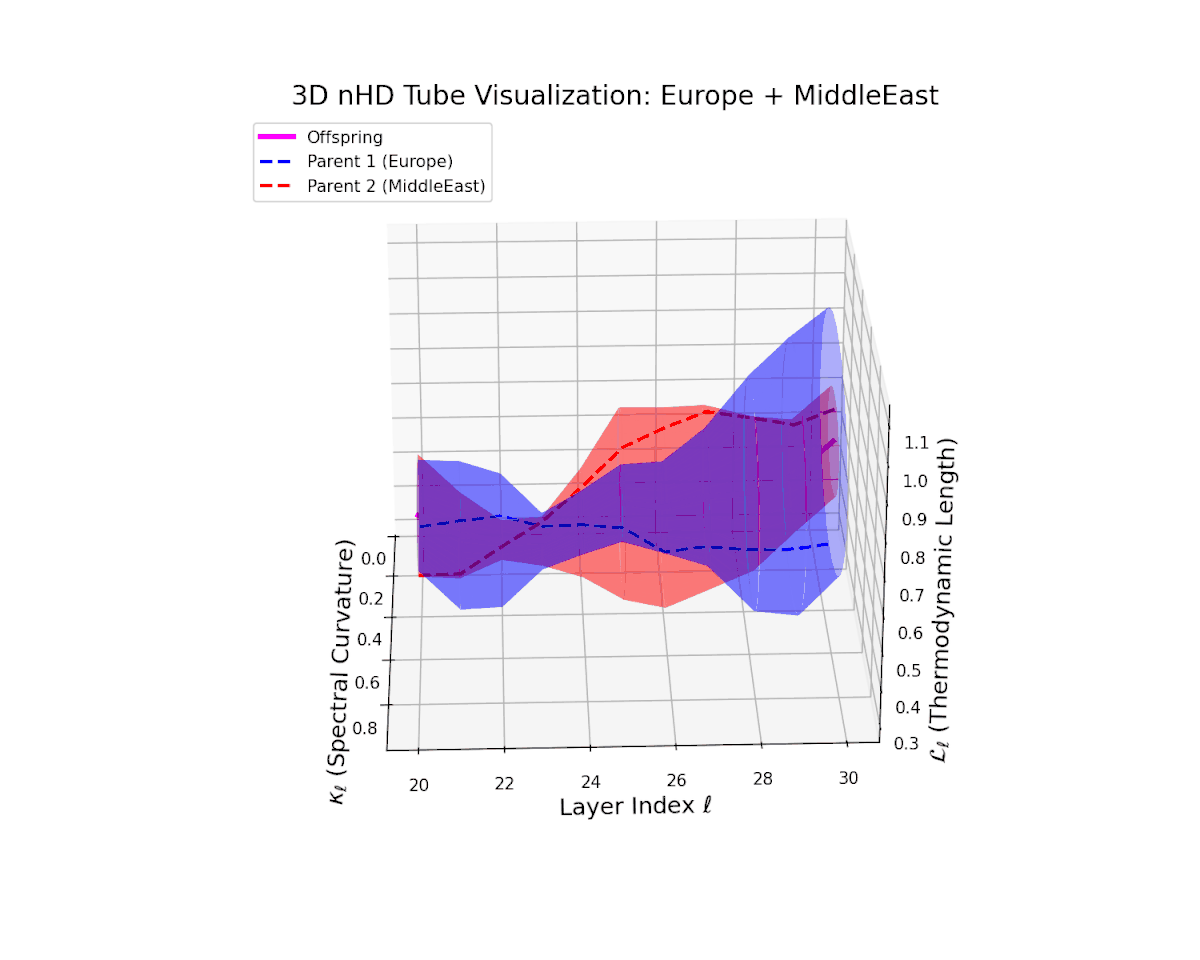
**(XVIII) Europe–Middle East Fusion**
The offspring latent manifold captures intricate semantic blending, with spectral curvature $\kappa_{\ell}$ increasing from $0.4$ to $0.85$. The thermodynamic length $L_{\ell}$ varies between $0.5$ and $1.0$, reflecting rich cumulative representational change. This complex interplay of parental semantic priors manifests in a geometrically diverse latent structure that balances cultural heterogeneity and integrative fusion.

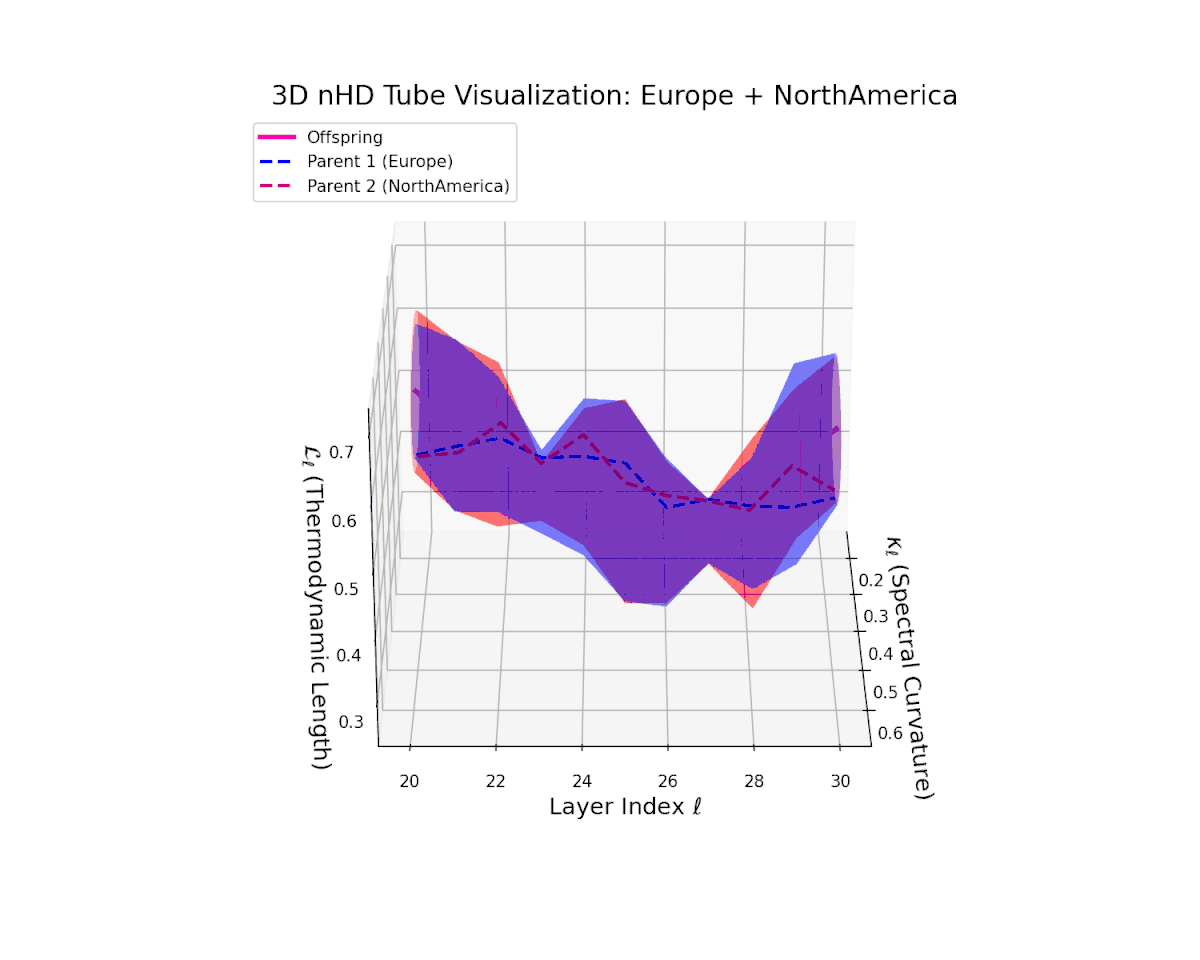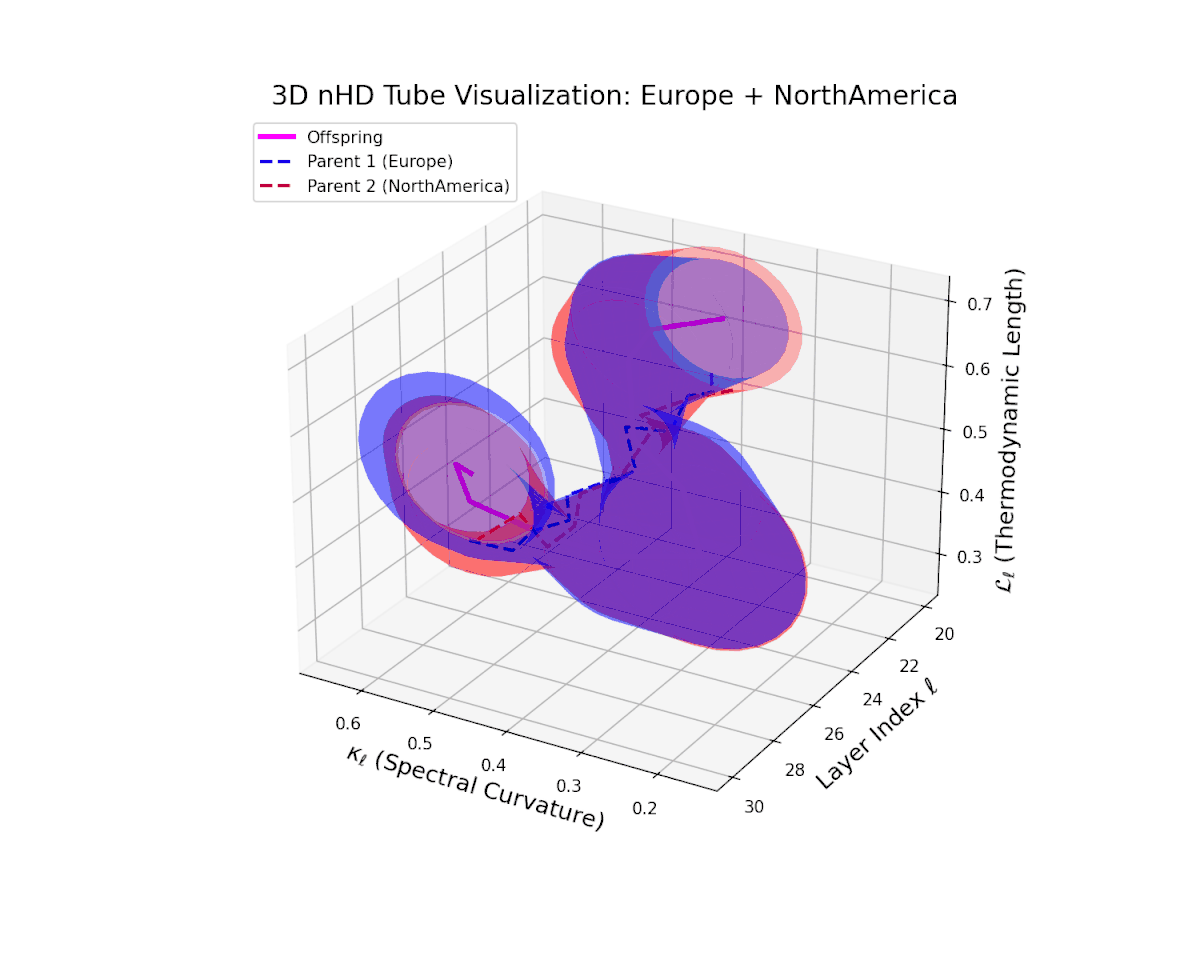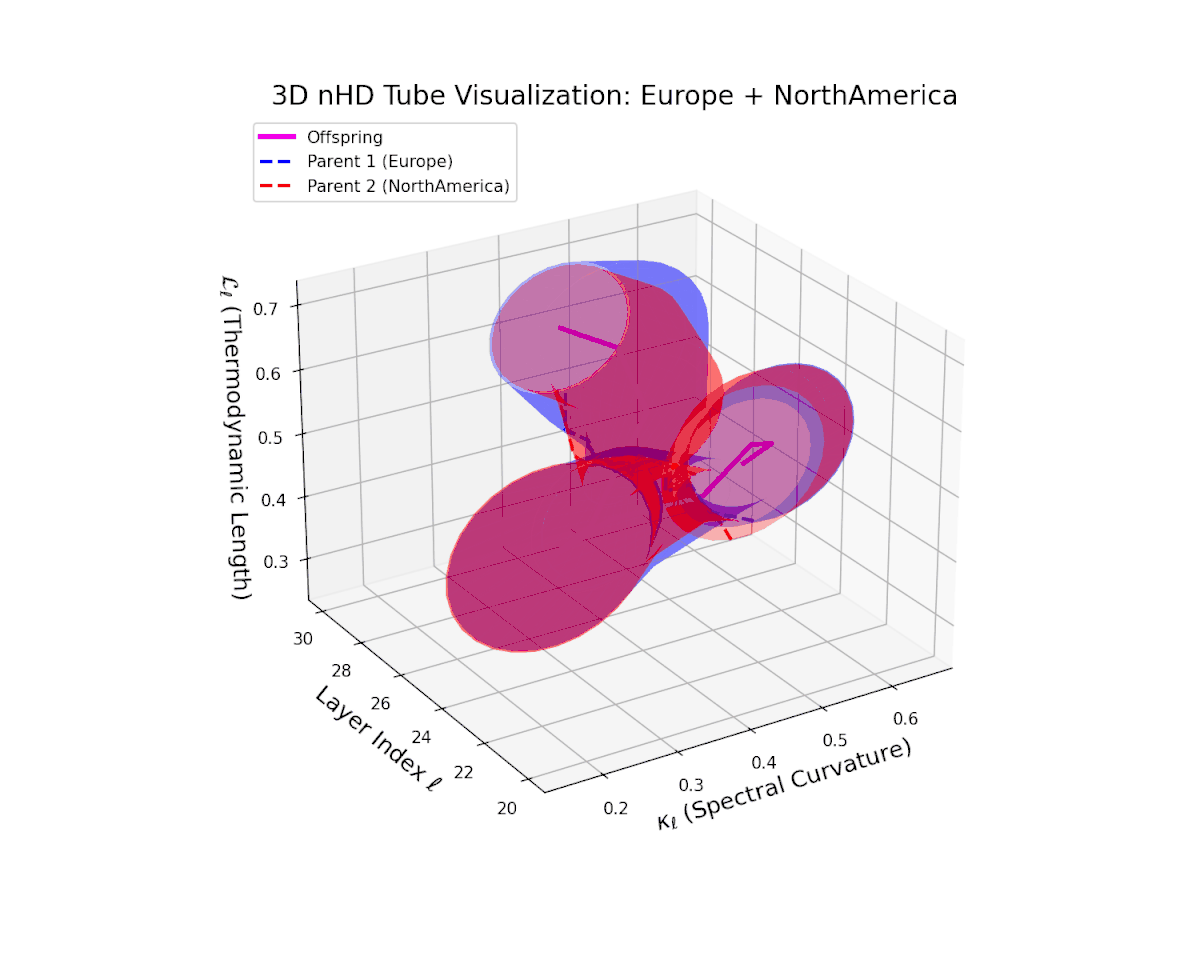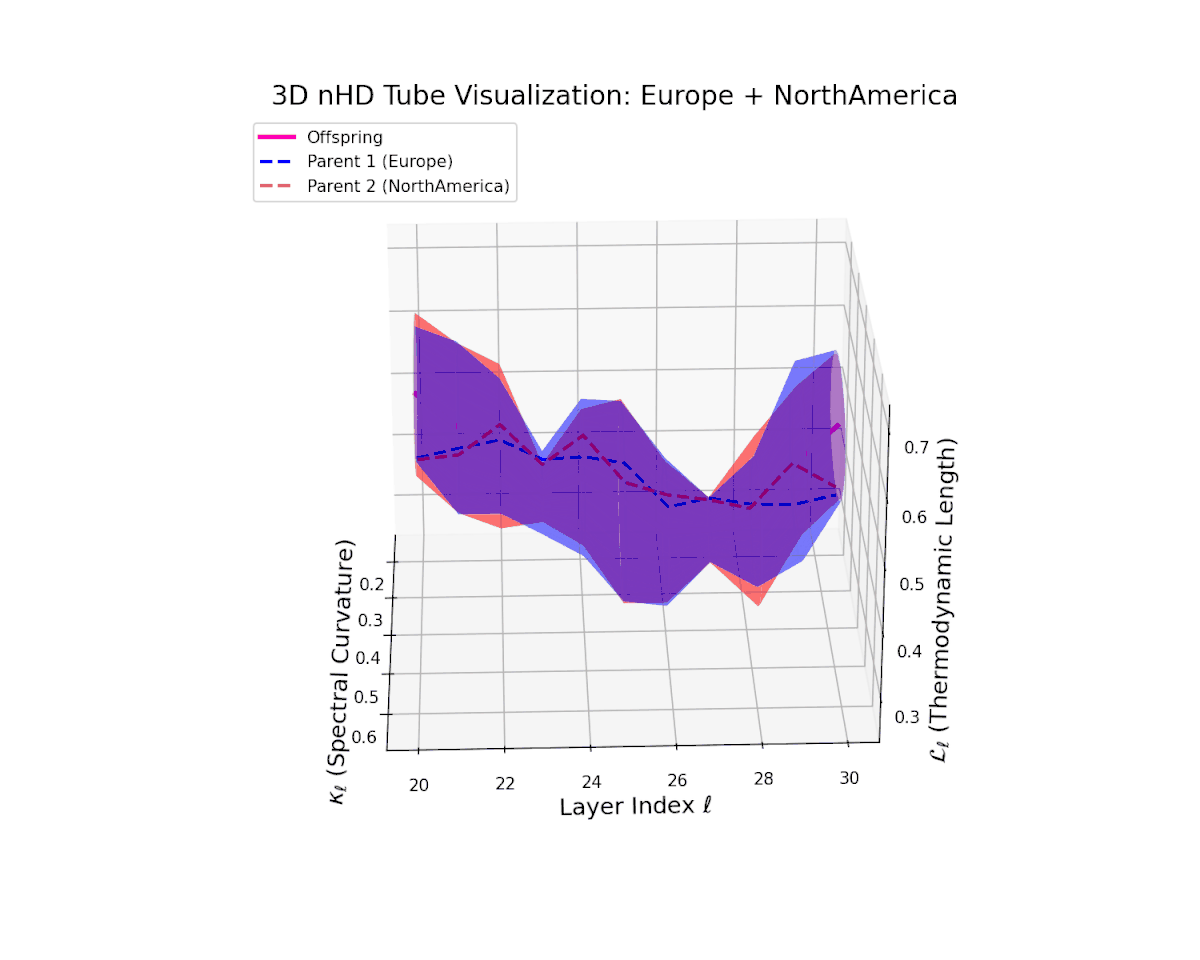
**(XIX) Europe–North America Fusion**
The offspring manifold (magenta) tightly traces a smooth latent path between parent manifolds, with spectral curvature $\kappa_{\ell}$ rising consistently from approximately $0.3$ to $0.75$. The thermodynamic length $L_{\ell}$ grows from $0.45$ to $0.95$, quantifying extensive cumulative semantic evolution. This smooth progression underscores stable and coherent semantic inheritance across late transformer layers in culturally related neural DNAs.

**(XX) Middle East–Latin America Fusion**
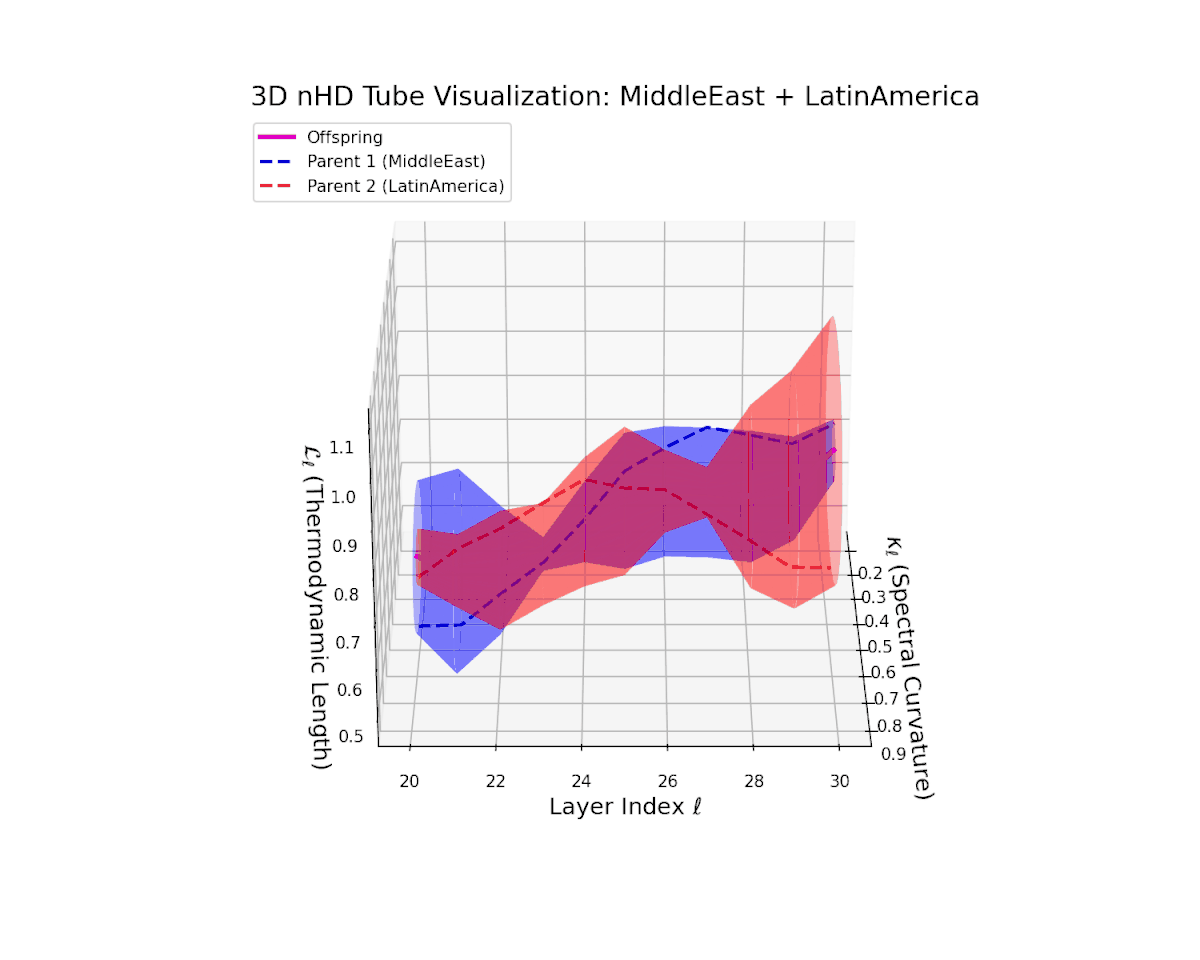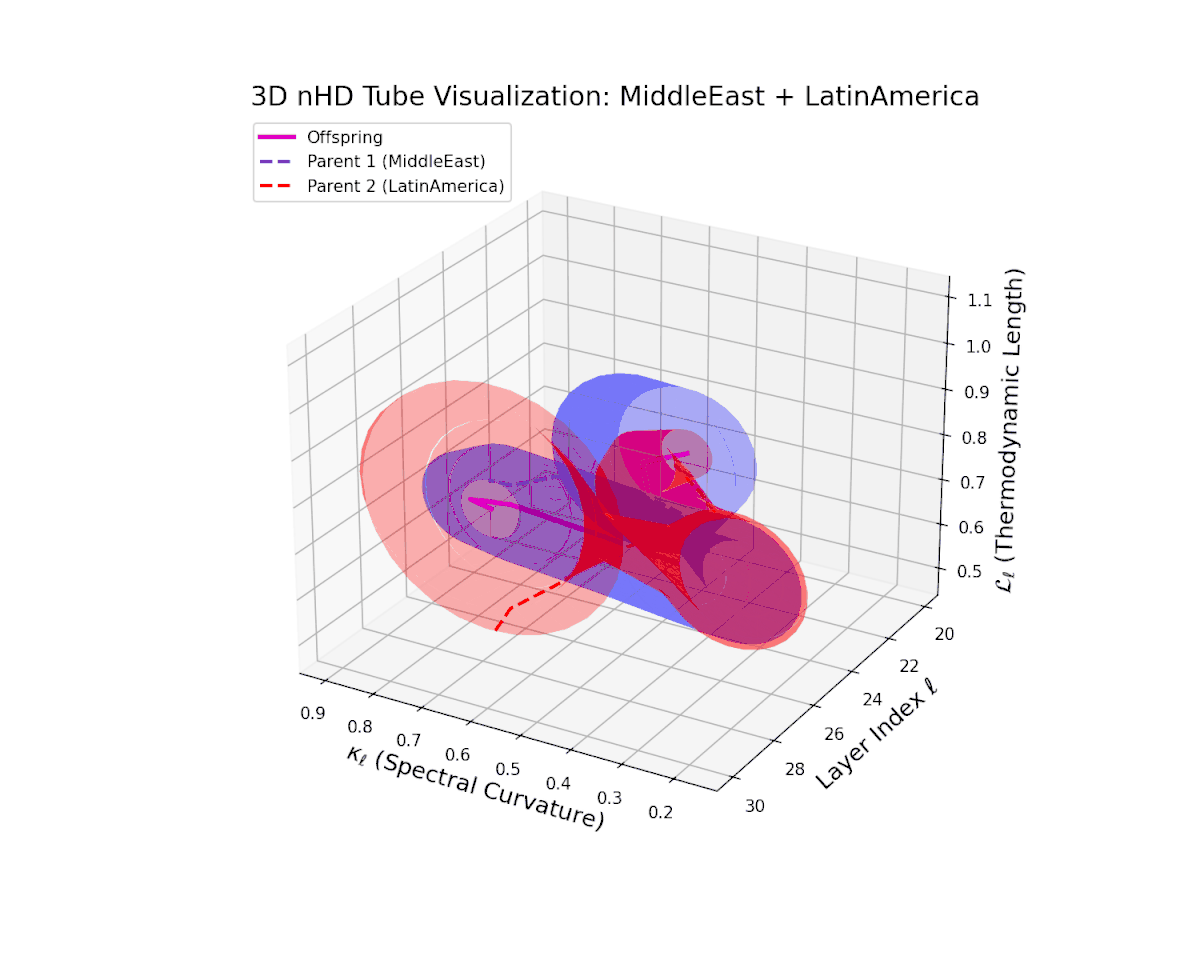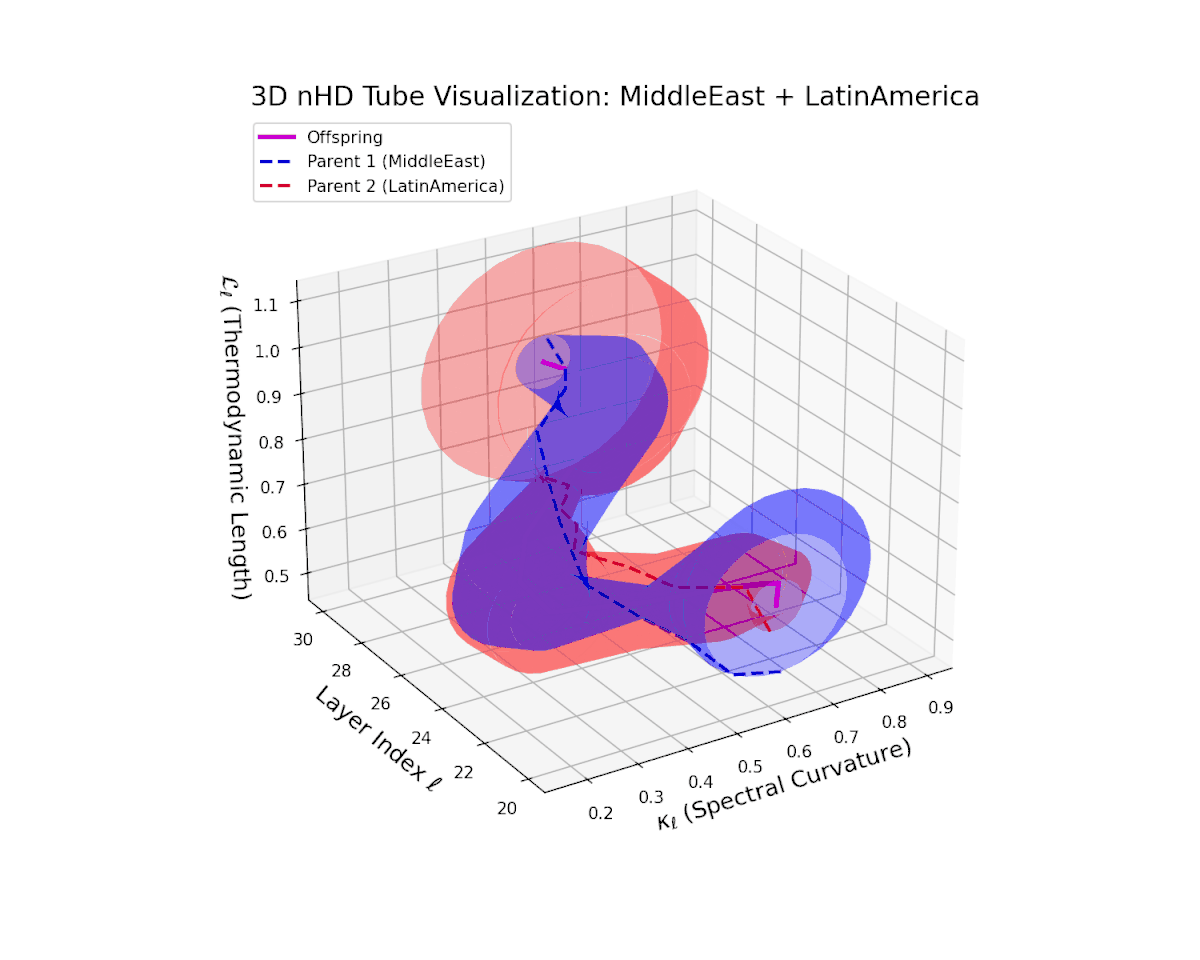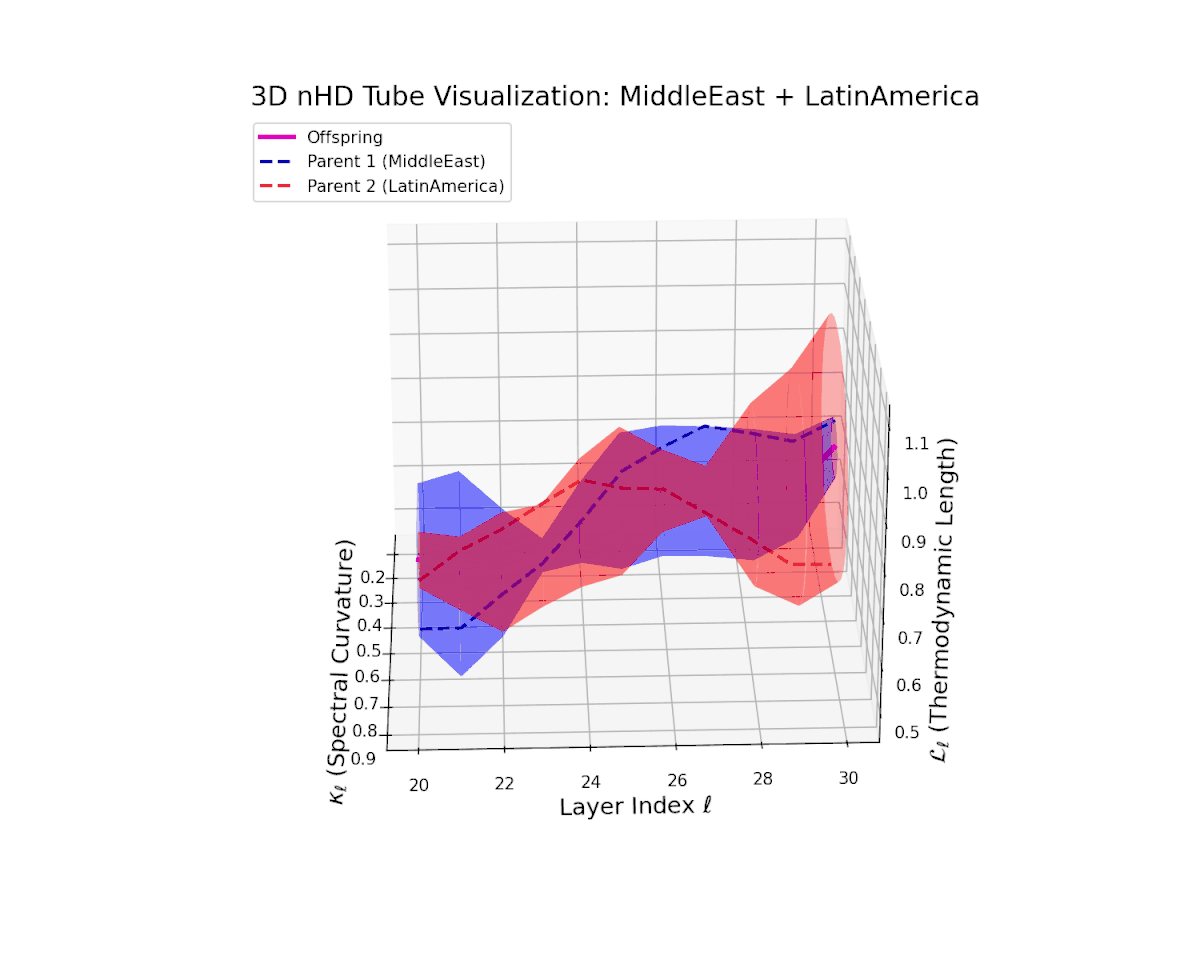
The offspring latent manifold (magenta solid) balances parental latent trajectories with spectral curvature $\kappa_{\ell}$ spanning from $0.35$ to $0.8$ and thermodynamic length $L_{\ell}$ increasing from $0.45$ to $0.9$. This smooth geometric evolution captures effective semantic fusion amid pronounced cultural diversity, reflecting a complex but stable integration of heterogeneous neural semantic priors.

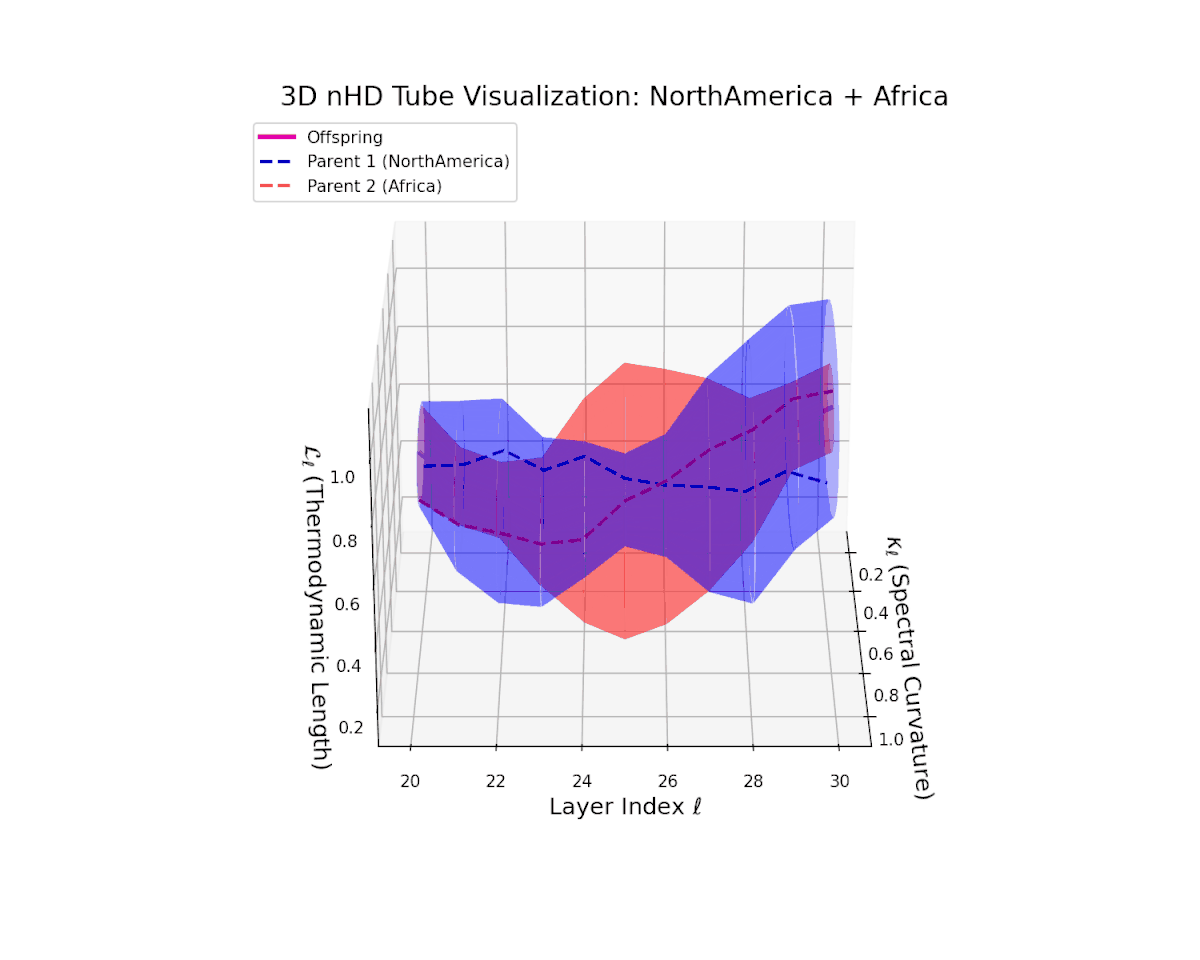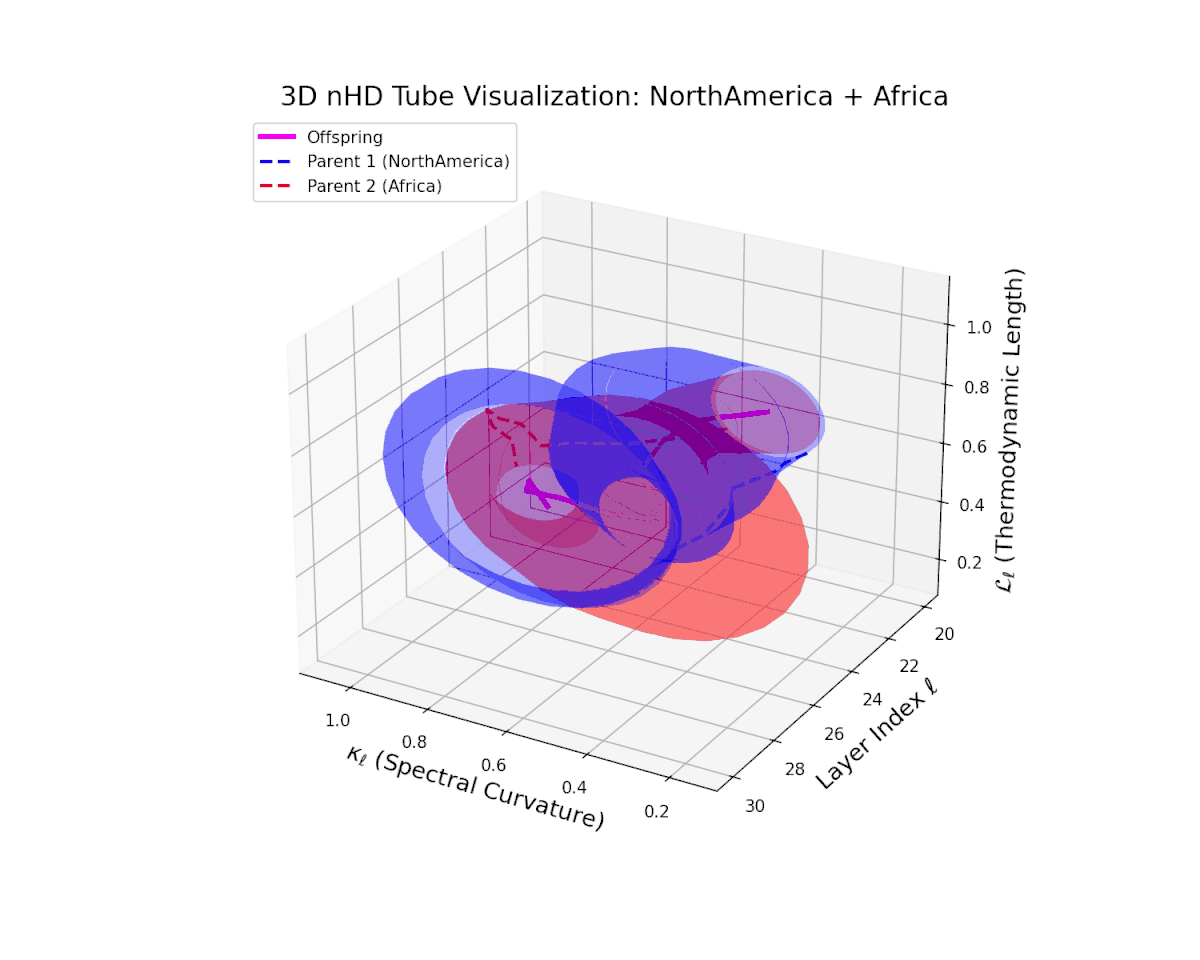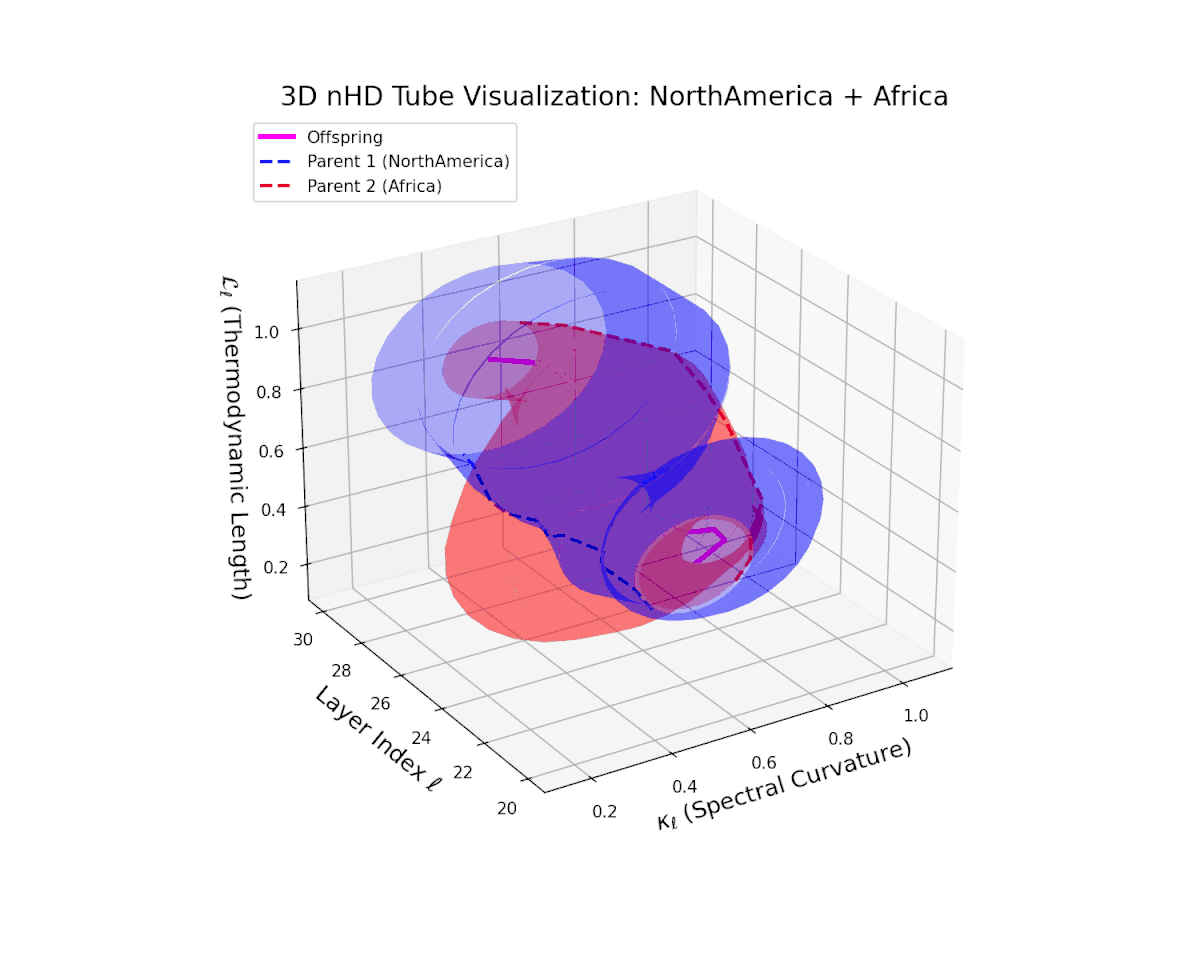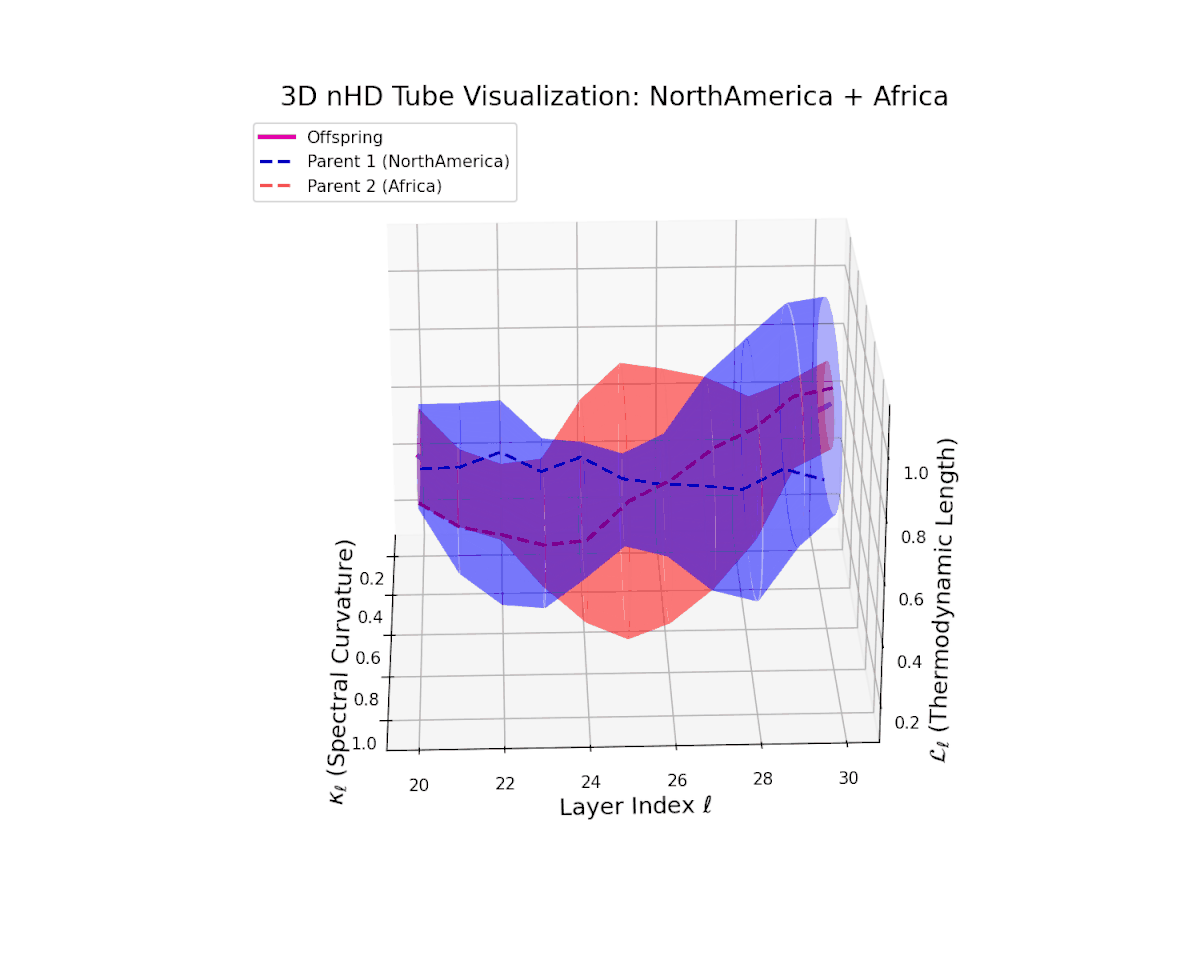
**(XXI) North America–Africa Fusion**
The offspring manifold (magenta) forms a smooth semantic bridge within the convex hull of parent manifolds (dashed blue and red). Spectral curvature $\kappa_{\ell}$ increases steadily from approximately $0.3$ to $0.75$, indicating growing local latent complexity and nonlinear bending. Thermodynamic length $L_{\ell}$ extends from $0.4$ to $0.9$, reflecting the cumulative semantic divergence and hierarchical feature transformation through layers $\ell = 20$ to $30$. This fusion embodies a sophisticated integration of diverse cultural semantic priors.

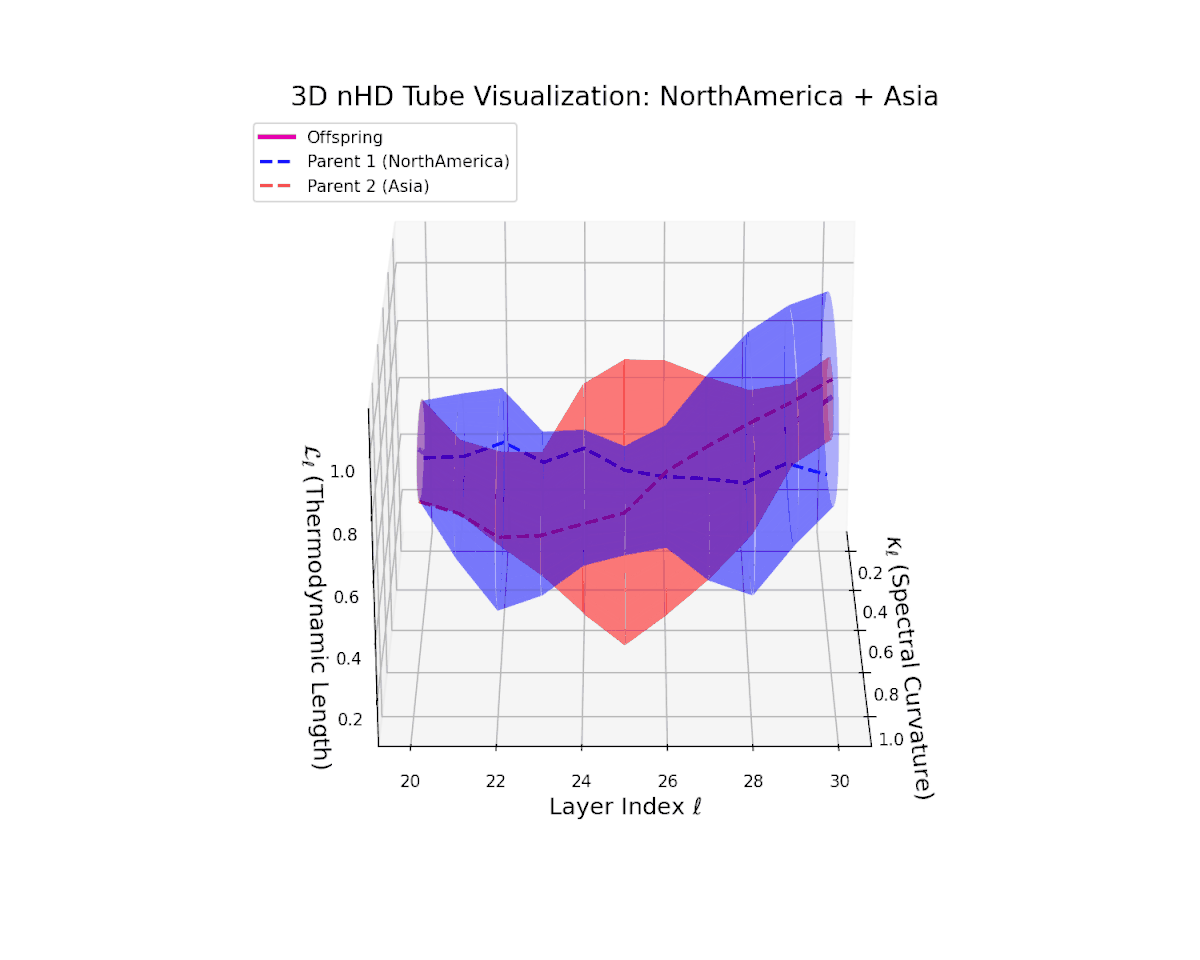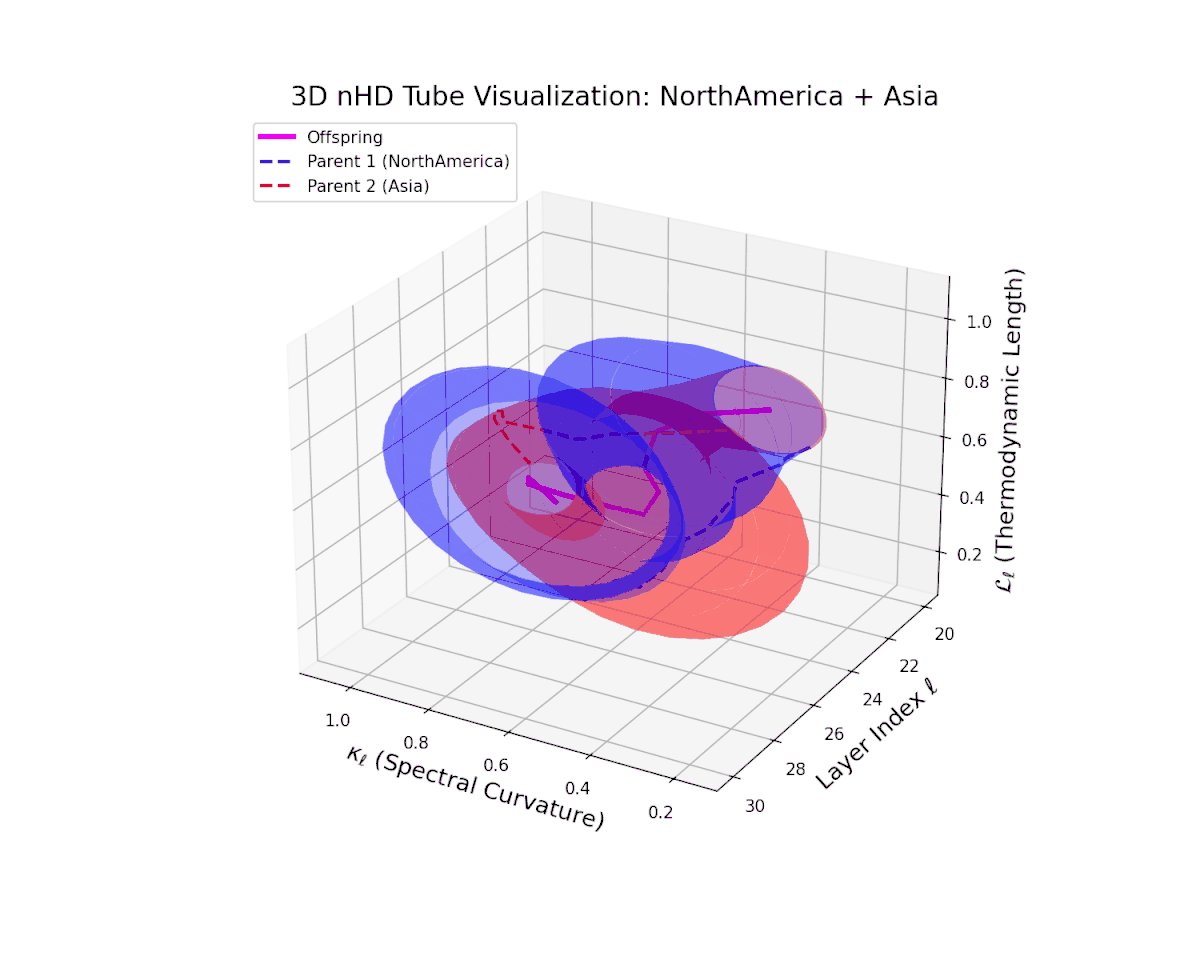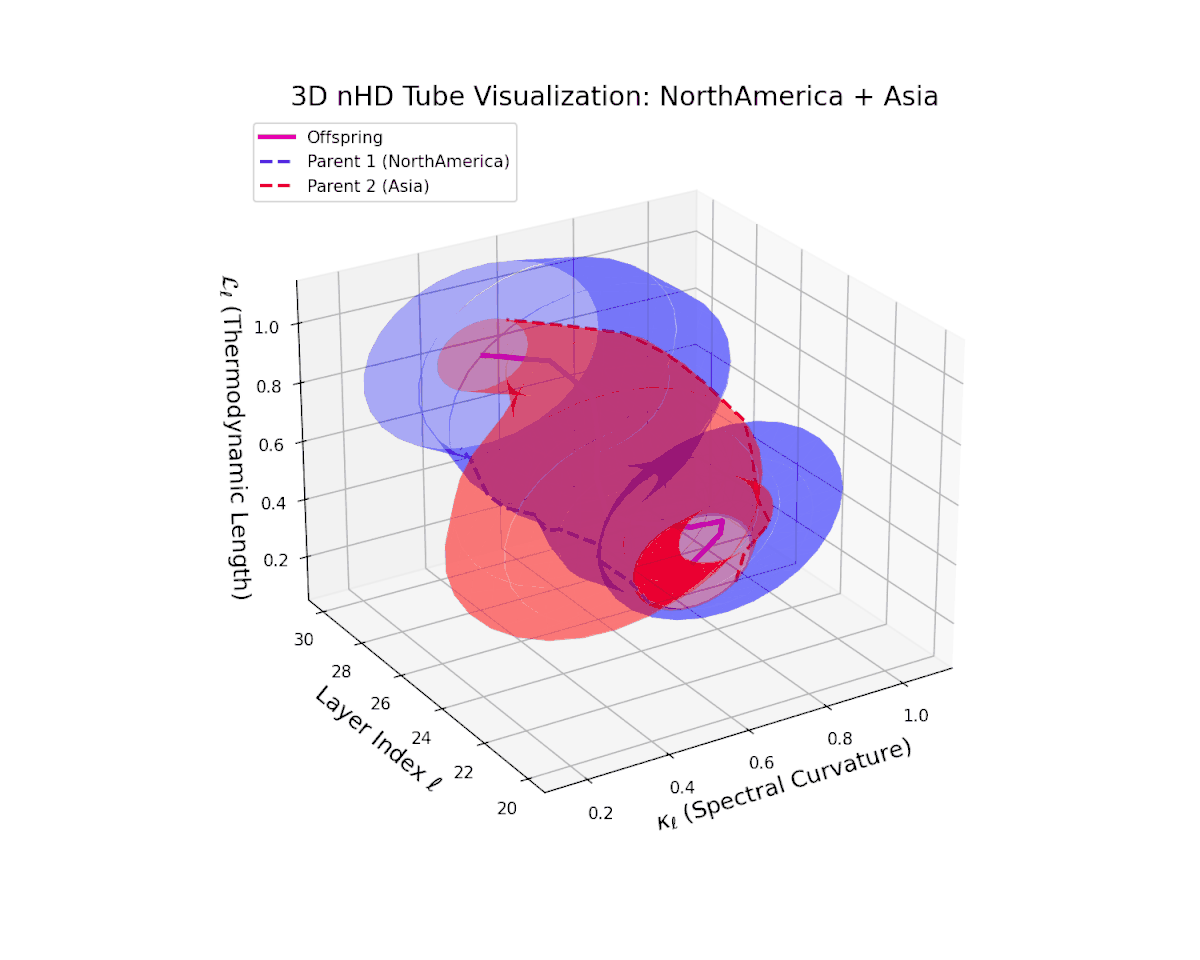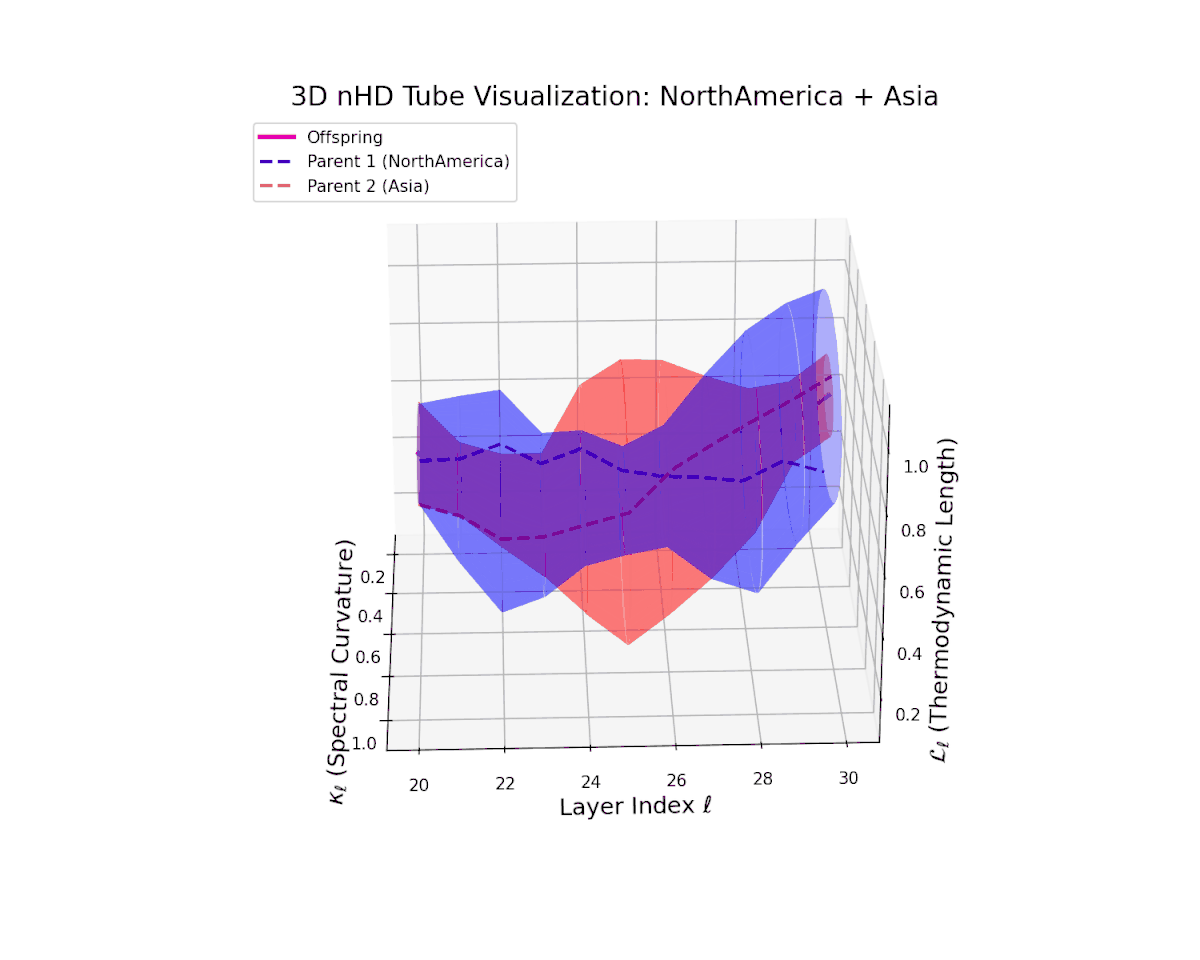
**(XXII) North America–Asia Fusion**
The offspring latent manifold smoothly traverses the convex latent space of parent manifolds, with spectral curvature $\kappa_{\ell}$ ascending from about $0.35$ to $0.8$. Concurrently, the thermodynamic length $L_{\ell}$ grows from $0.45$ to $0.95$, denoting layered semantic compositionality and progressive information geometric deformation. This trajectory reflects a rich blend of culturally distinct latent semantic features integrated through deep transformer layers.

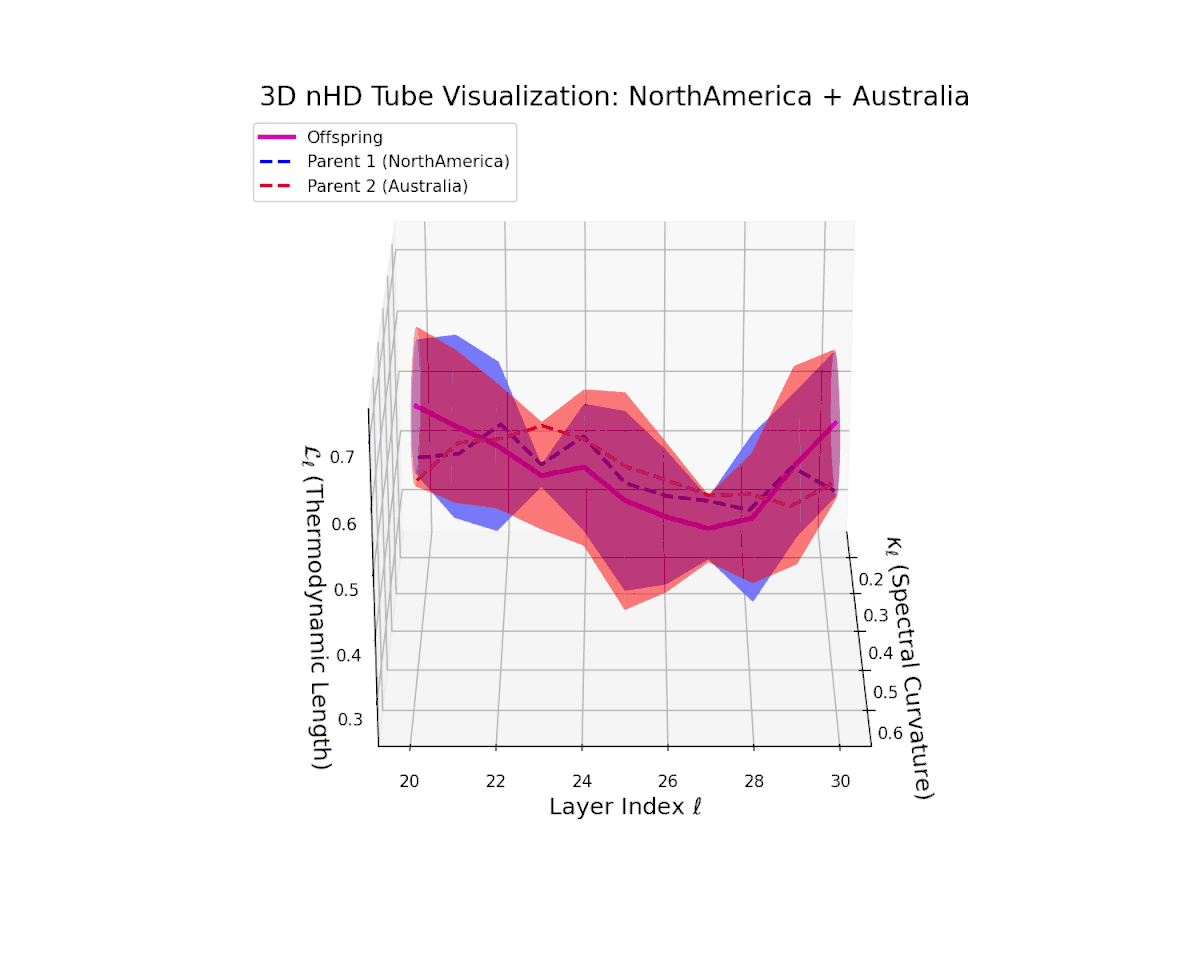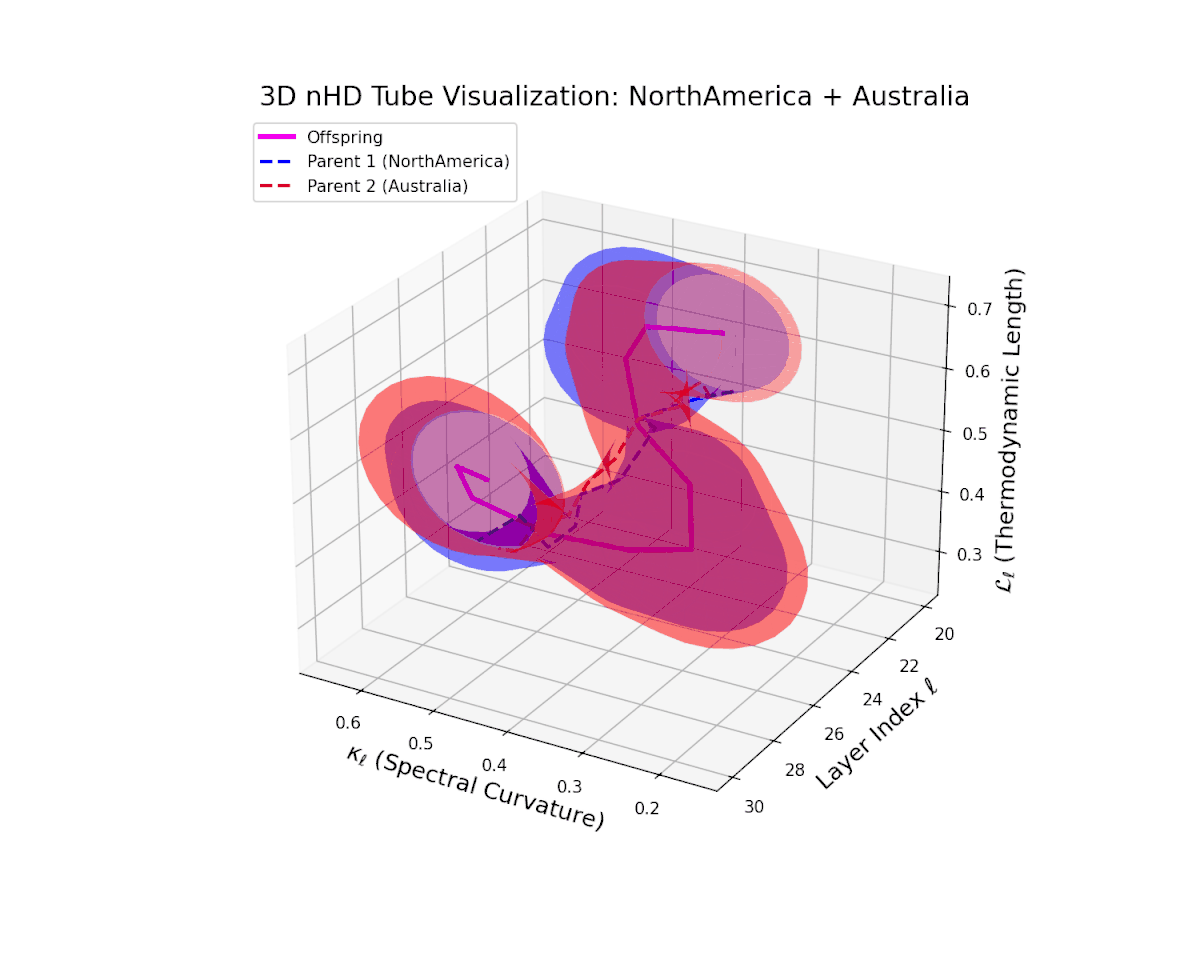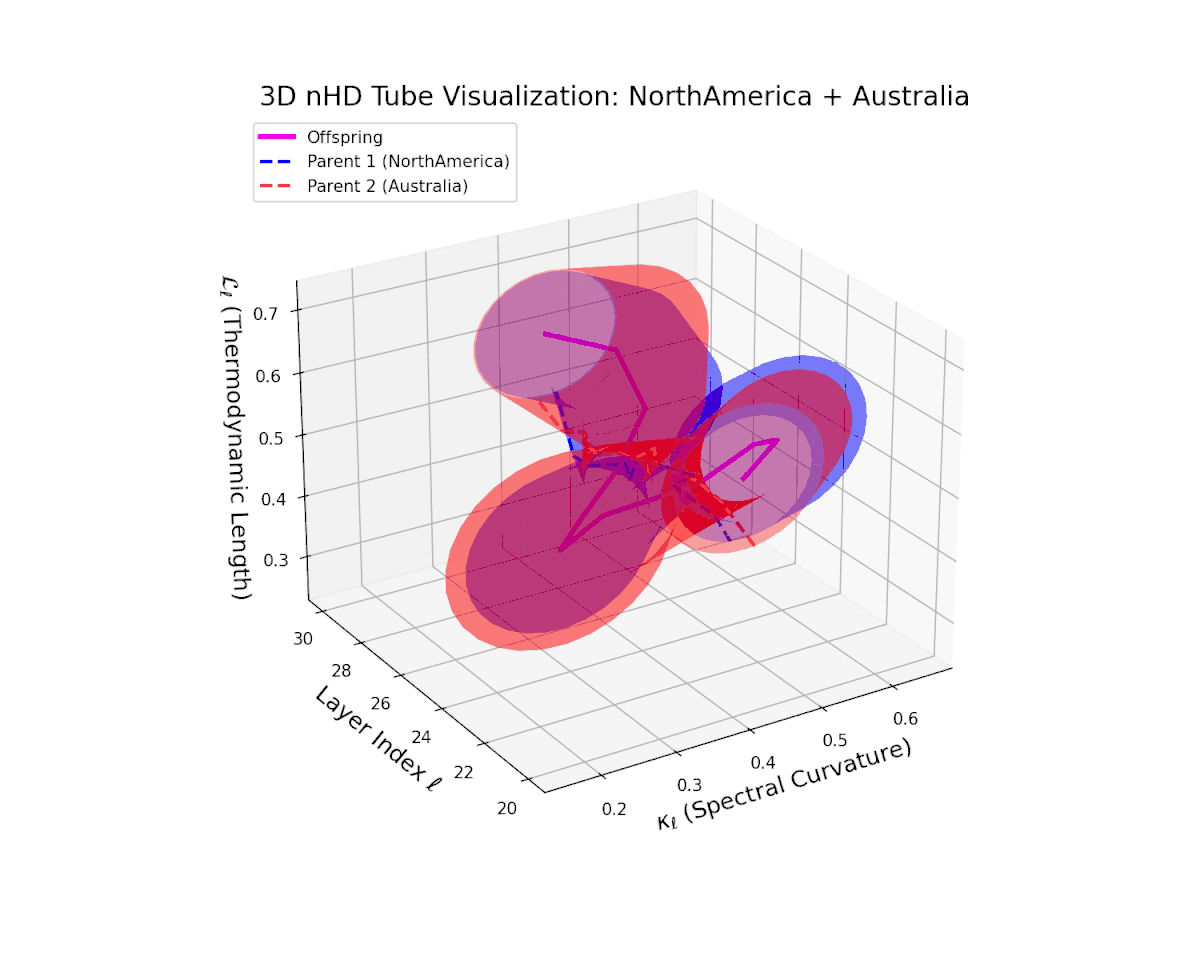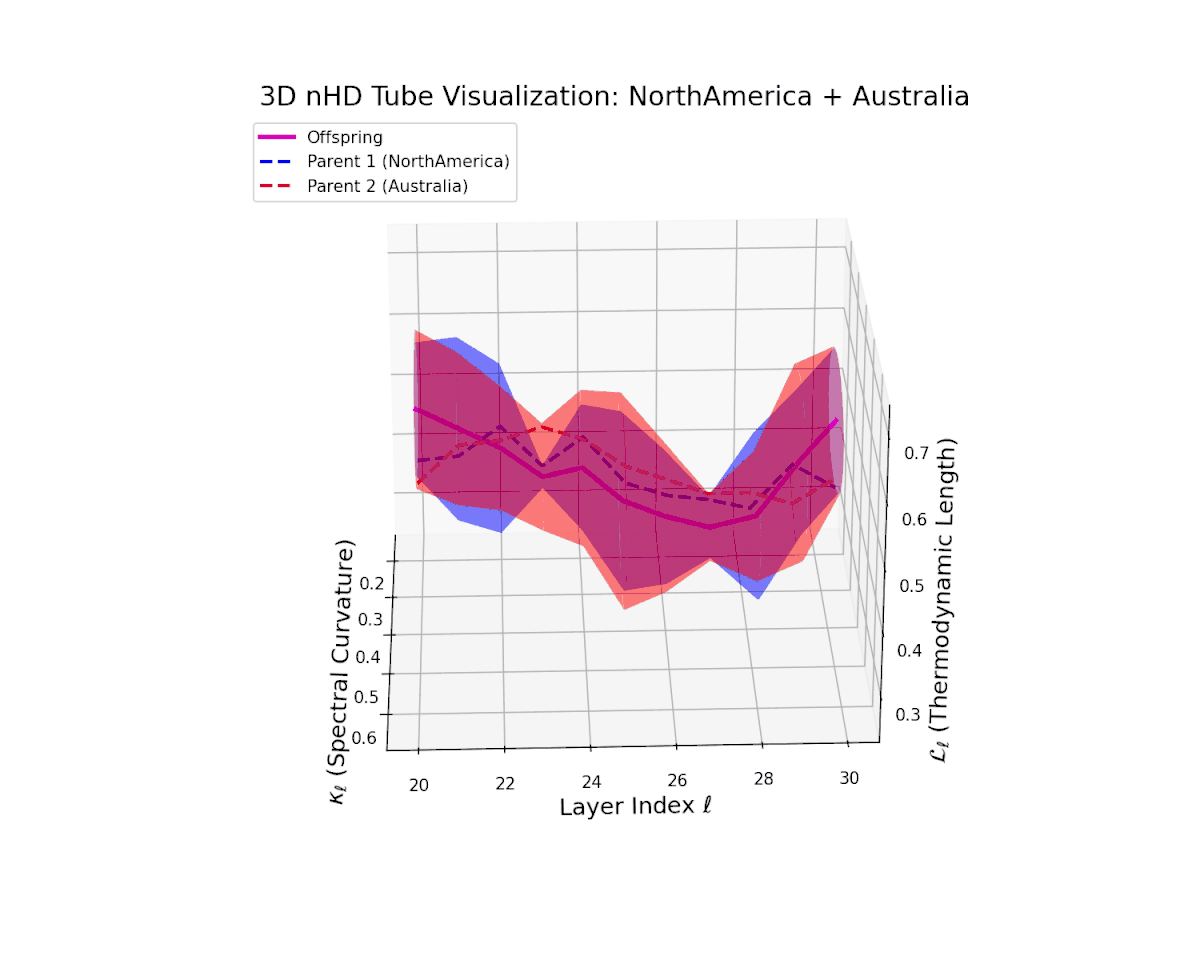
**(XXIII) North America–Australia Fusion**
The offspring manifold (magenta) interpolates parental manifolds with spectral curvature $\kappa_{\ell}$ rising from approximately $0.3$ to $0.7$. Thermodynamic length $L_{\ell}$ extends from $0.35$ to $0.85$, indicating continuous cumulative semantic change within the latent space. This smooth fusion underscores effective integration of geographically and culturally distinct neural DNAs into coherent semantic representations.

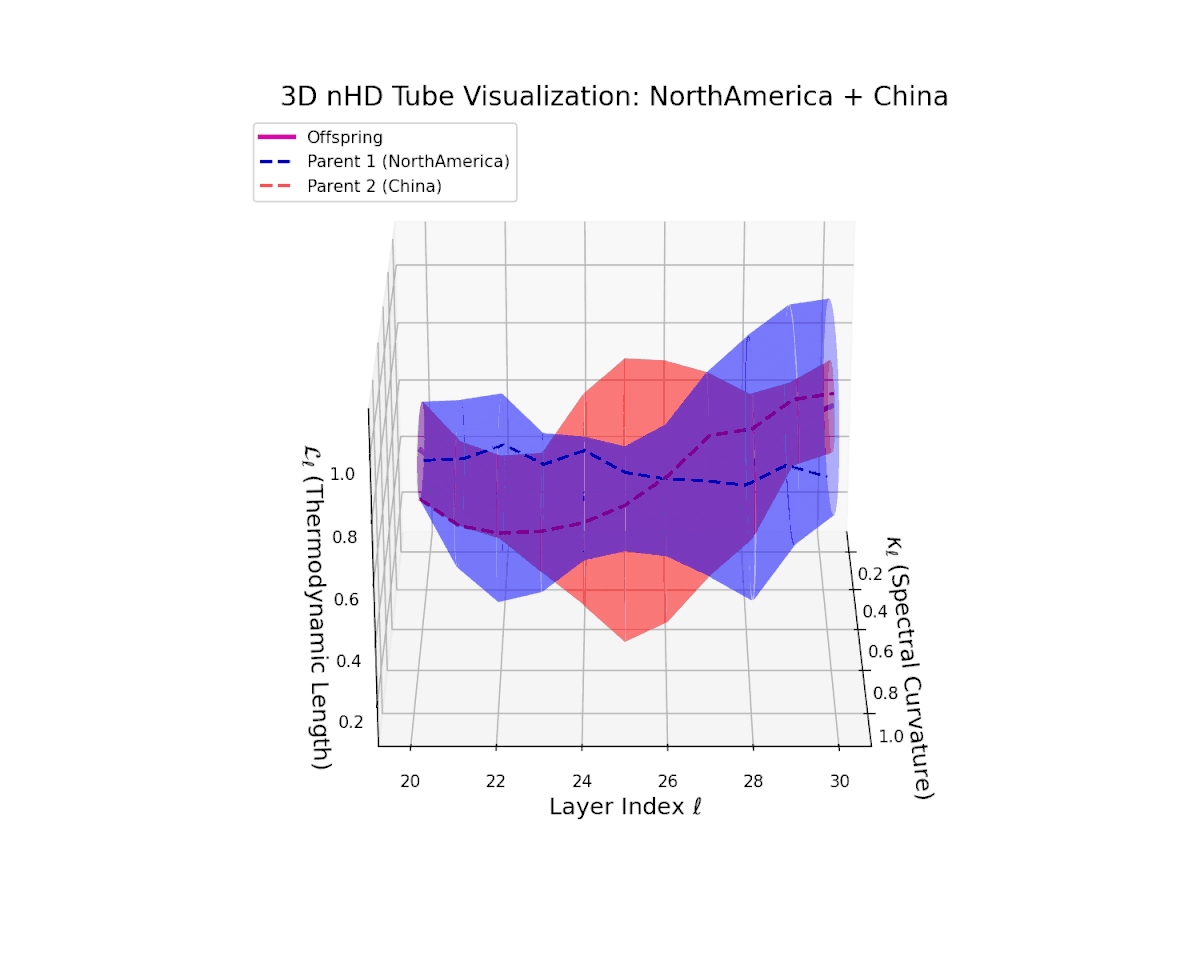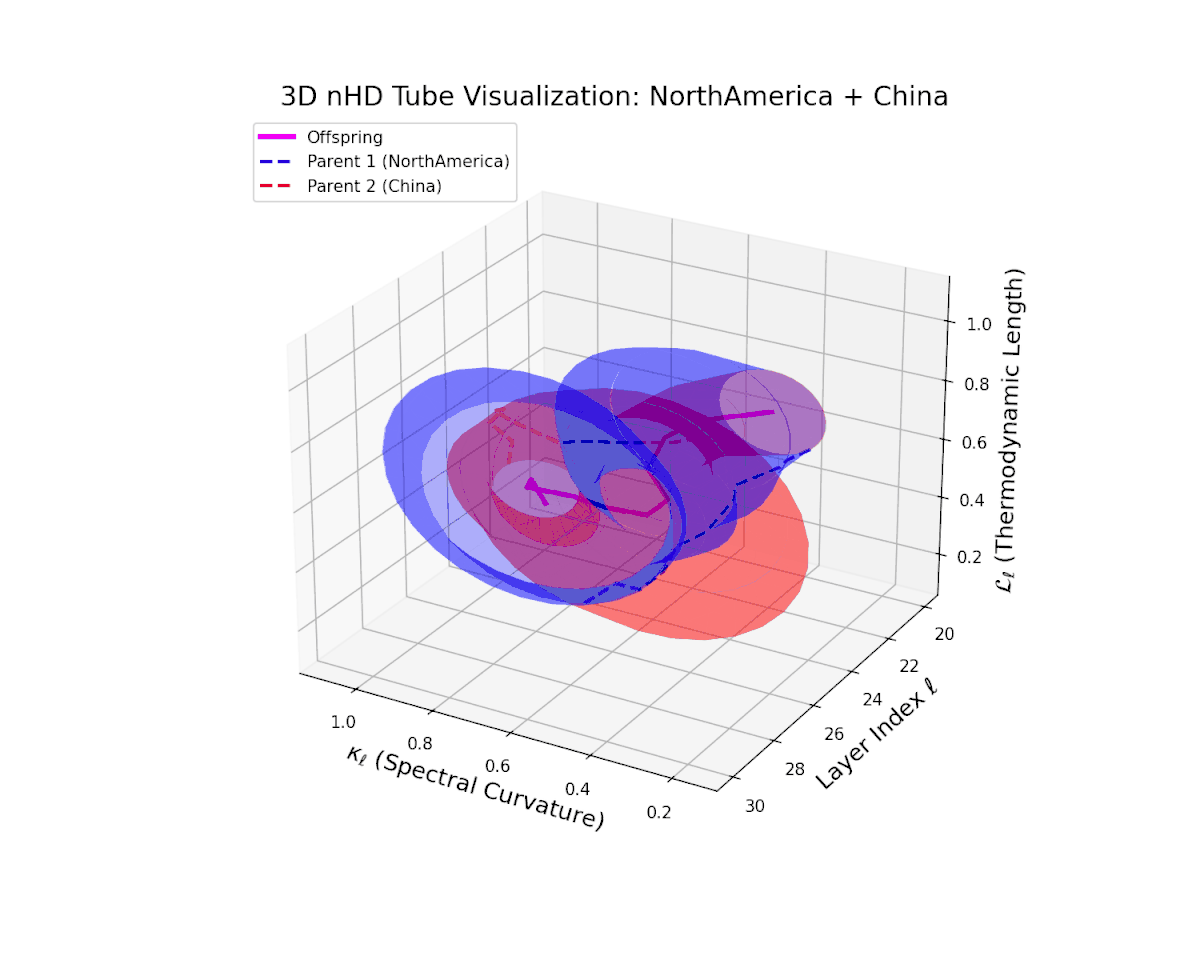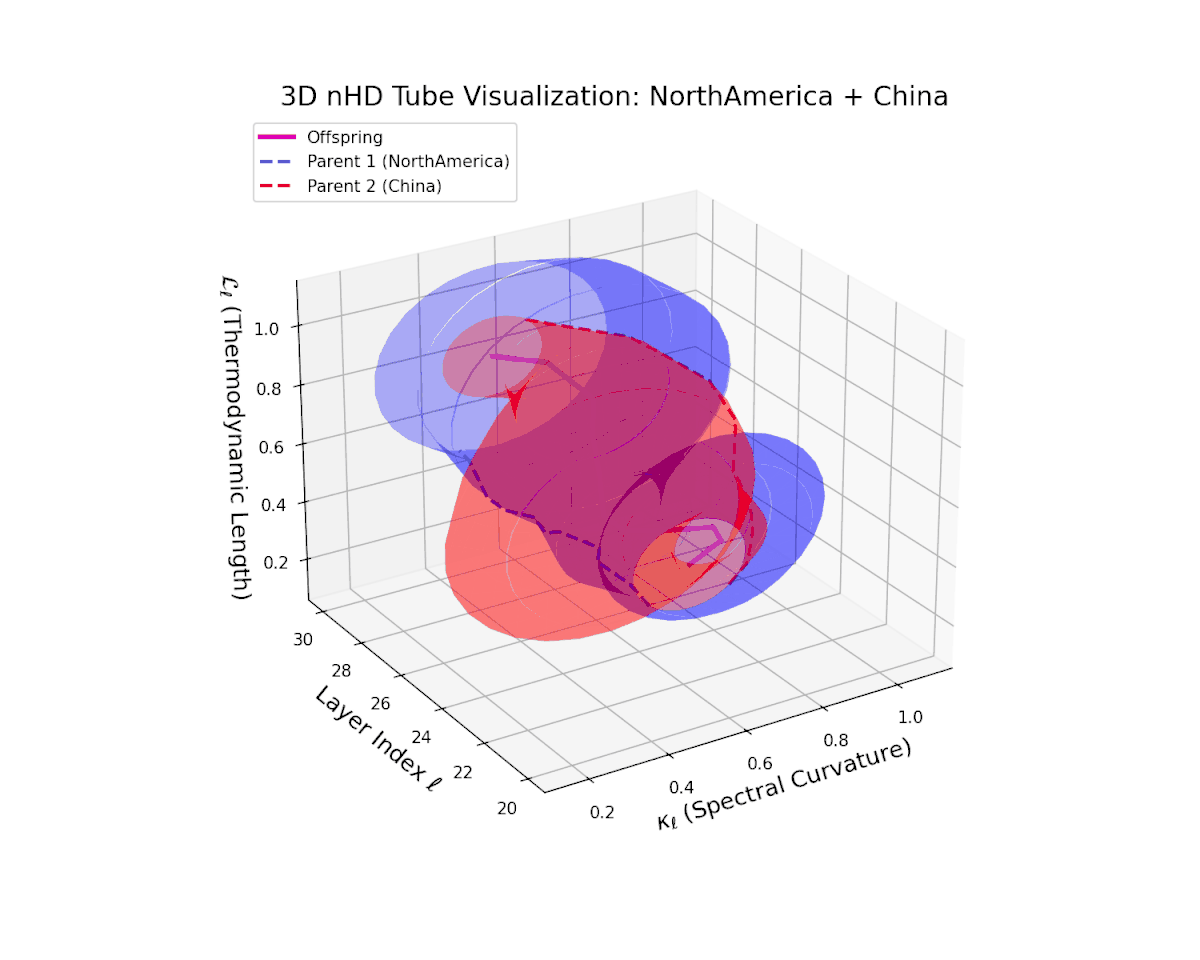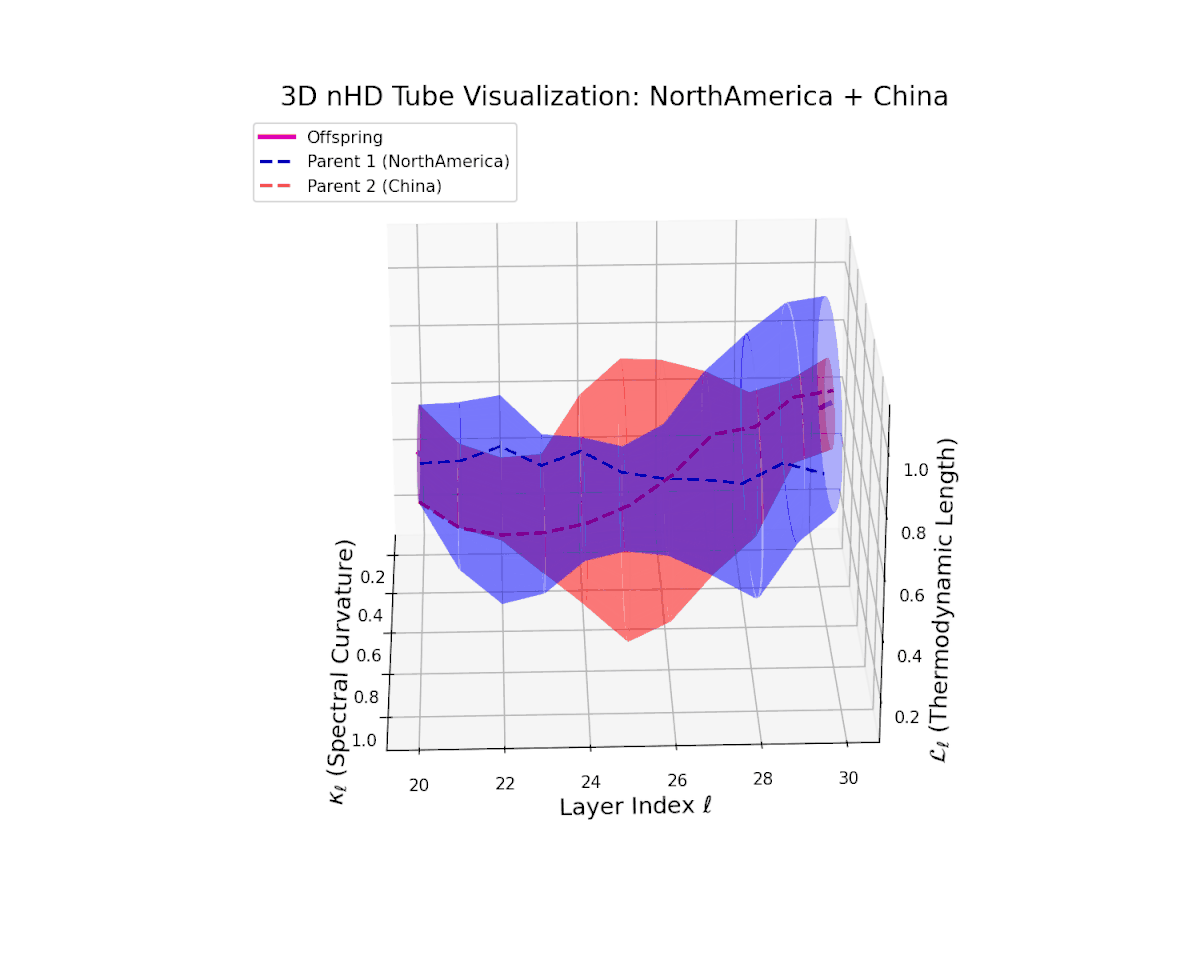
**(XXIV) North America–China Fusion**
The offspring latent manifold gradually evolves within the convex latent space of its parents, with spectral curvature $\kappa_{\ell}$ rising steadily from $0.35$ to $0.8$ and thermodynamic length $L_{\ell}$ increasing from $0.4$ to $0.9$. This trajectory reveals nuanced hierarchical semantic fusion and cumulative geometric deformation, reflecting rich cross-cultural semantic interactions within the transformer’s latent space.

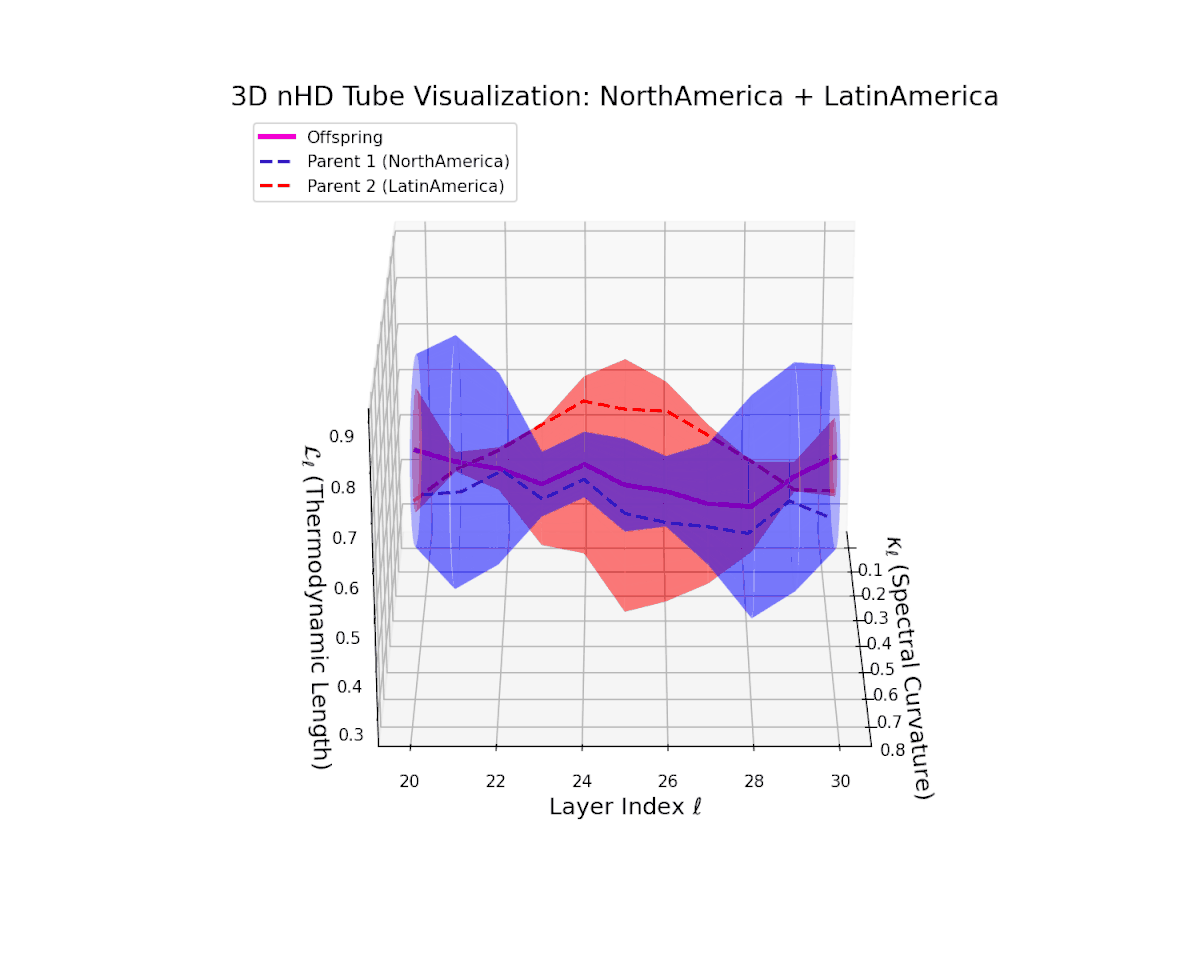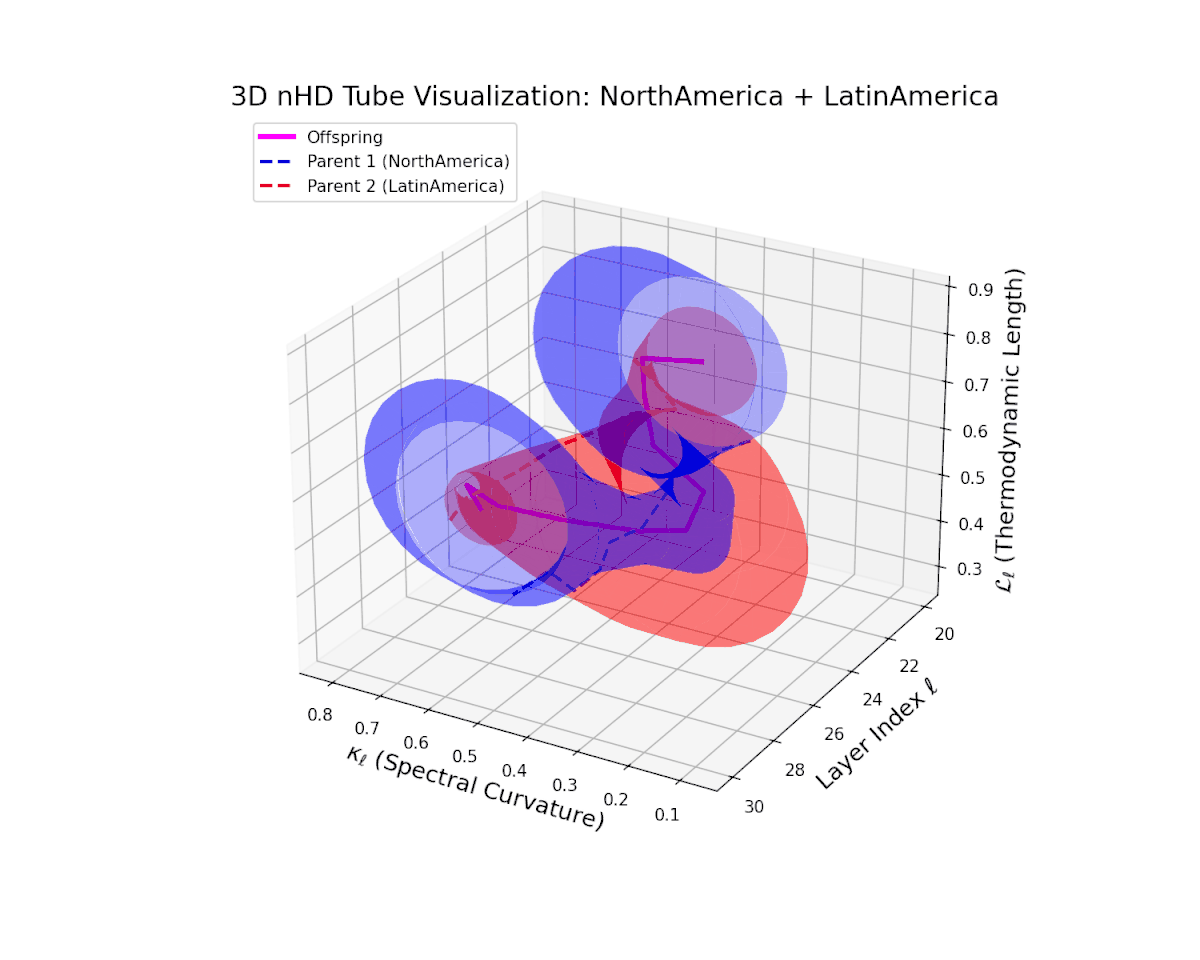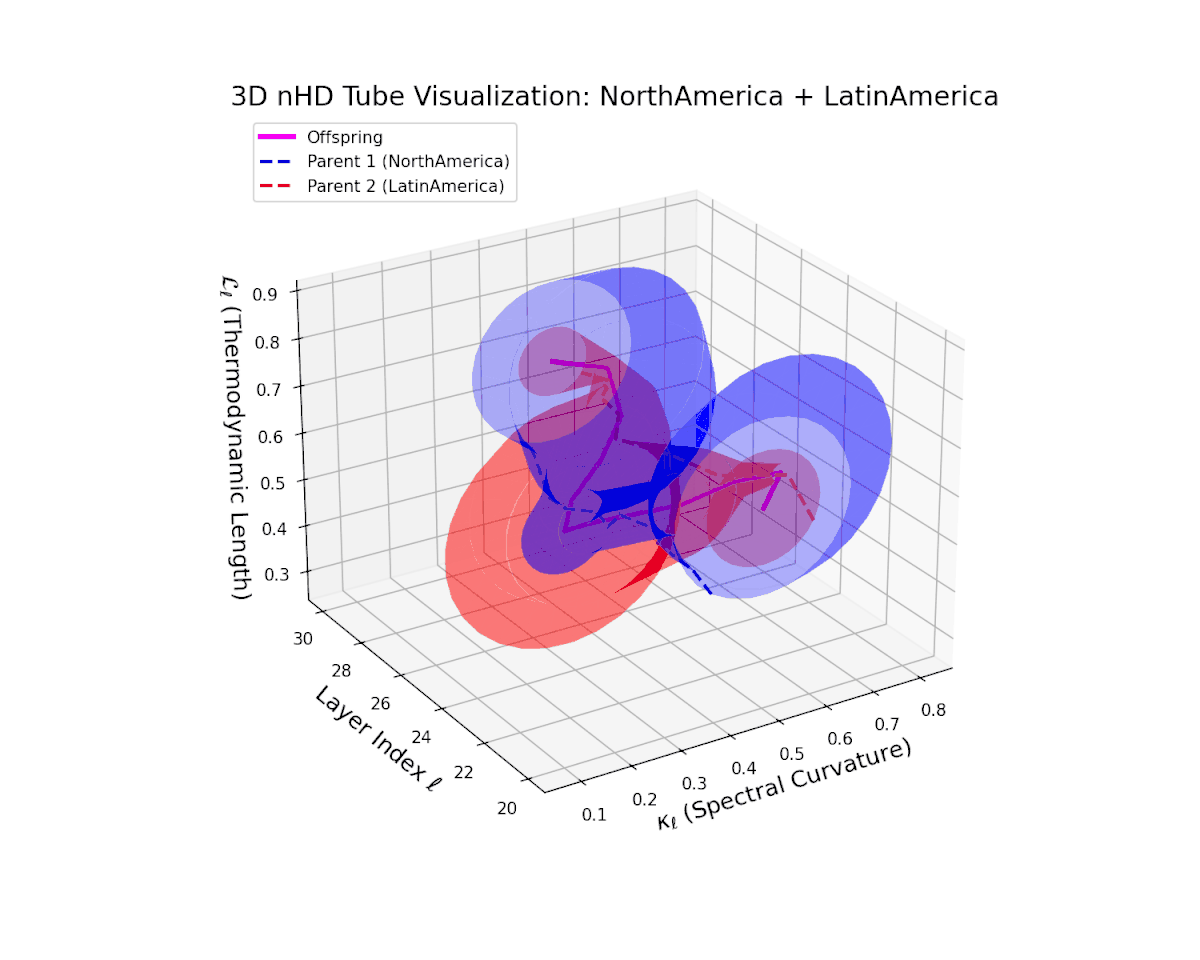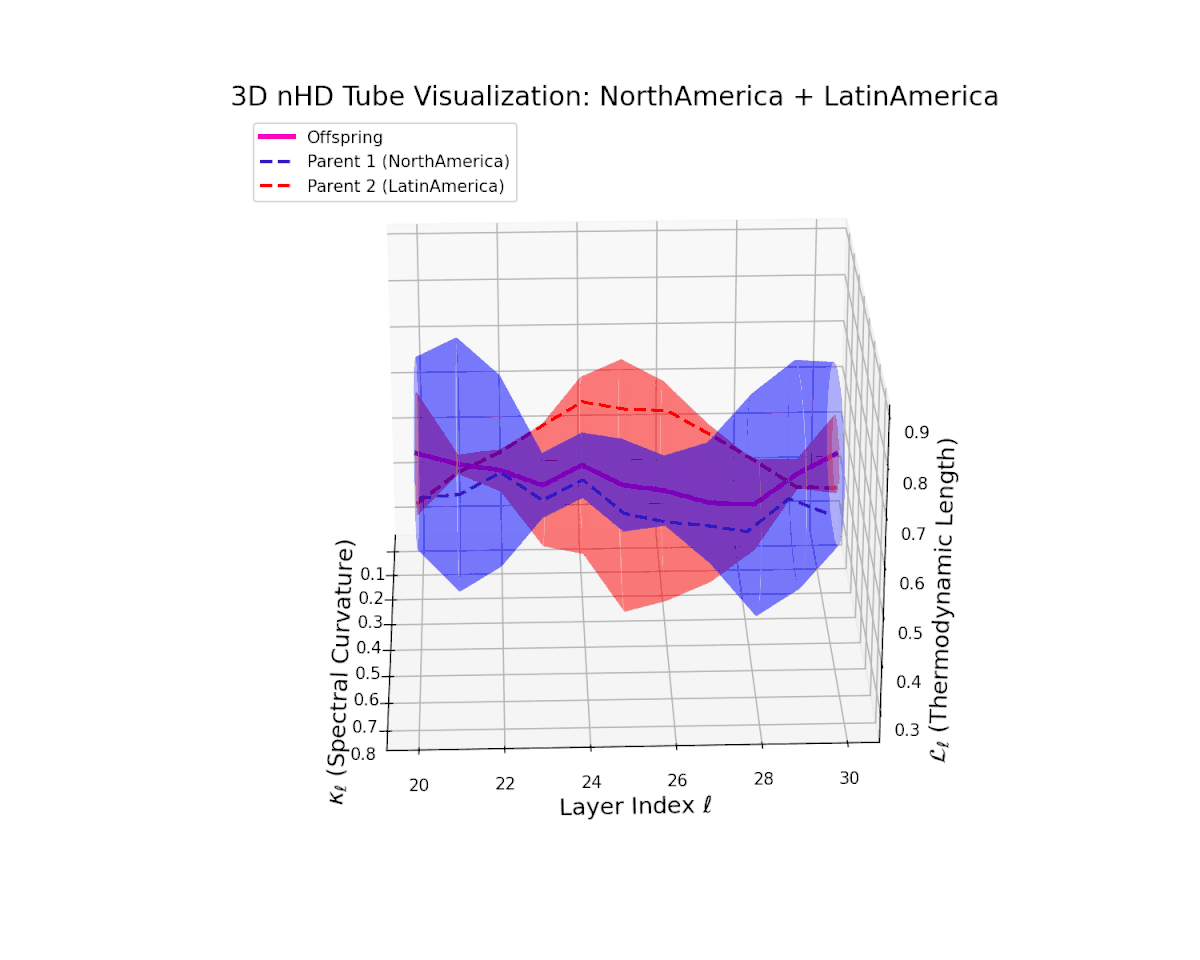
**(XXV) North America–Latin America Fusion**
The offspring latent manifold (magenta) smoothly traverses between parents, with spectral curvature rising from $0.3$ to $0.75$ and thermodynamic length growing from $0.45$ to $0.9$. This reflects coherent semantic integration shaped by closely related cultural influences.

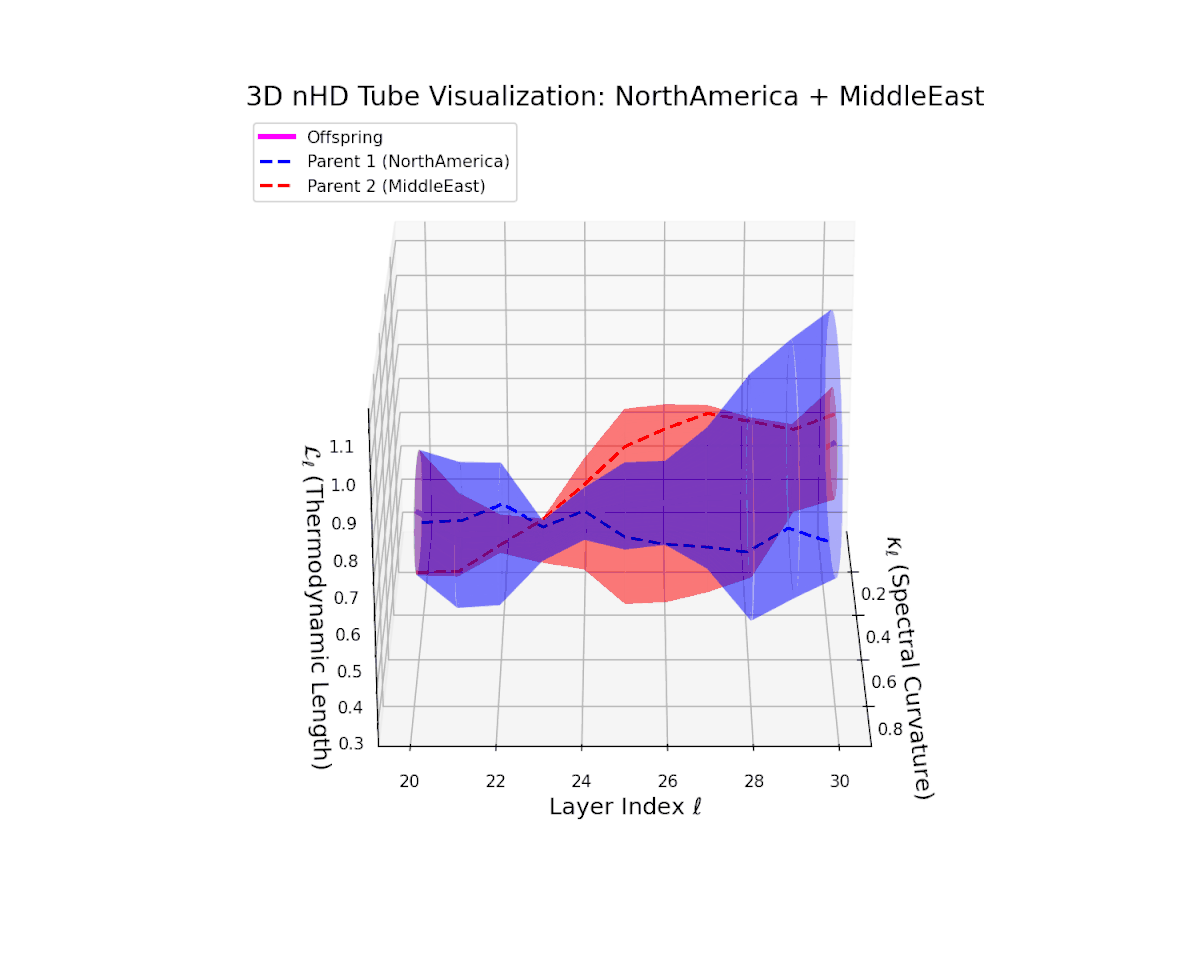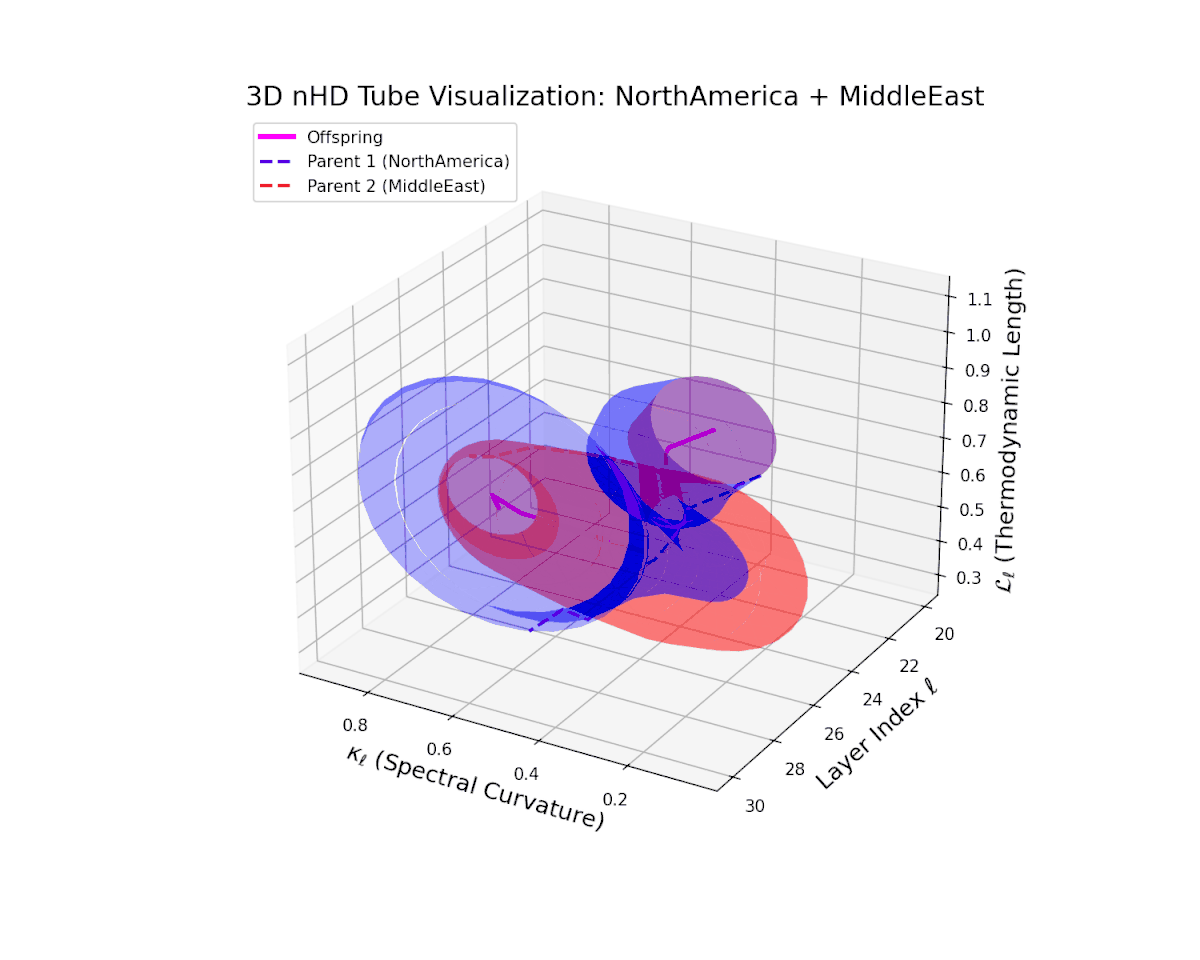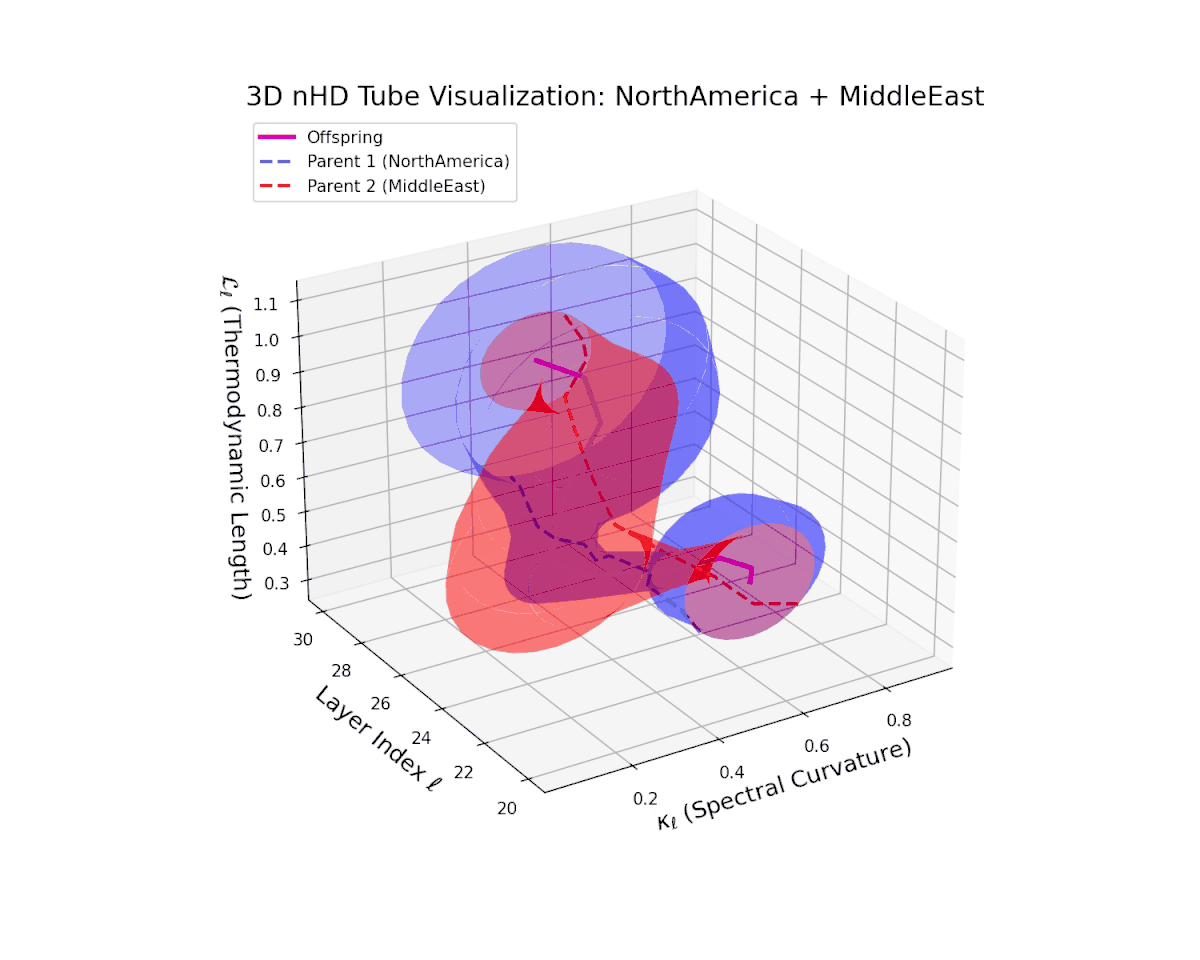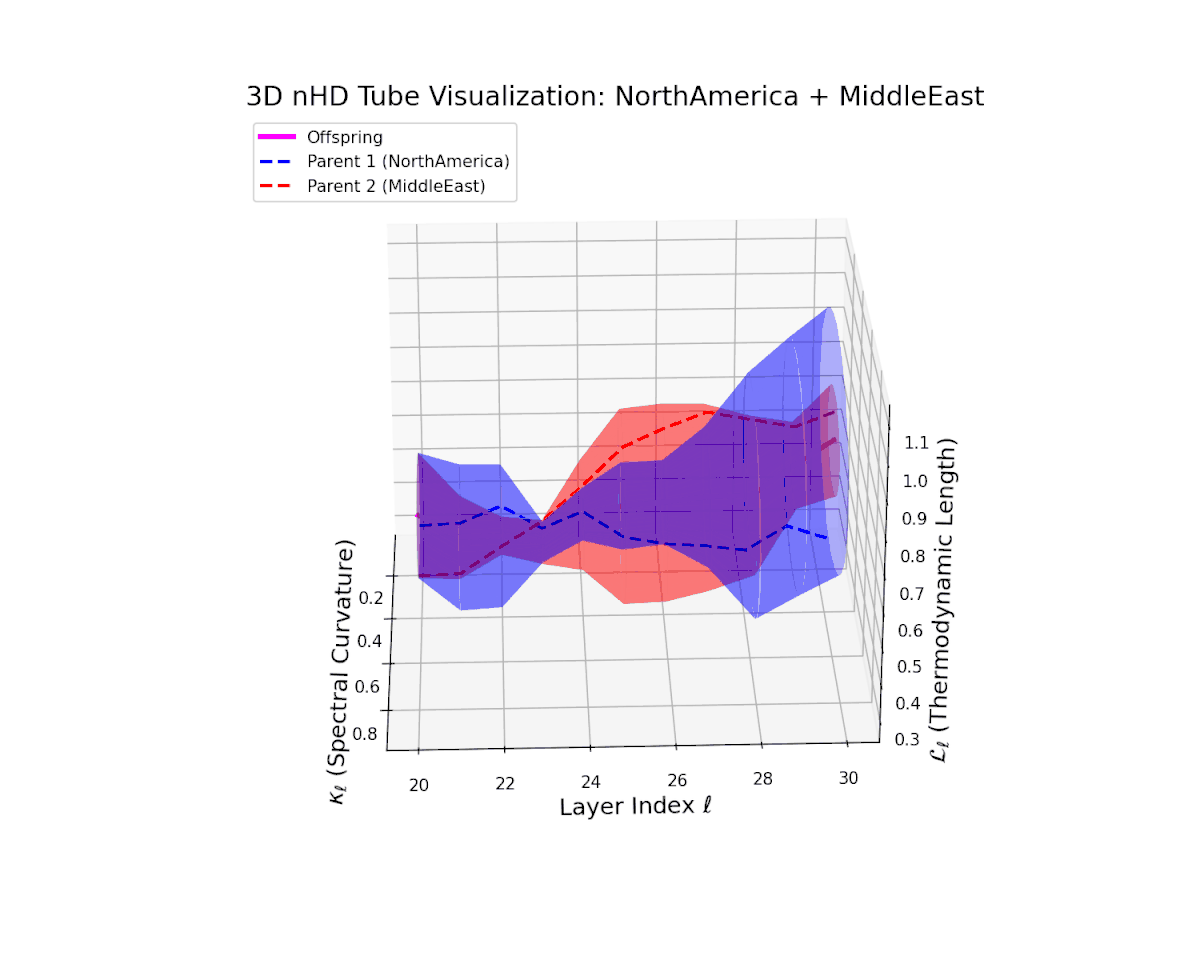
**(XXVI) North America–Middle East Fusion**
The offspring manifold shows a smooth latent interpolation bounded by parents, with spectral curvature rising from $0.35$ to $0.8$ and thermodynamic length increasing from $0.4$ to $0.95$. This reflects complex semantic fusion across heterogeneous cultural neural DNAs via continuous geometric deformation.

**(XXVII) Middle East–Latin America Fusion**
The offspring manifold (magenta solid) balances parental latent geometries, with spectral curvature spanning $0.35$ to $0.8$ and thermodynamic length increasing from $0.45$ to $0.9$. This geometric blending reflects stable semantic fusion across culturally diverse variants, with smooth manifold deformation.

**(XXVIII) Asia–Latin America Fusion**
The offspring latent manifold (magenta) lies within the convex hull of parental manifolds, with spectral curvature rising from $0.3$ to $0.8$ and thermodynamic length growing from $0.45$ to $0.95$. This indicates a smooth and rich fusion of semantic priors, capturing layered nonlinear compositionality and cumulative semantic change.

Figure: nHD Tube Visualizations of Offspring Latent Manifolds: The offspring manifold (magenta solid) is bounded by parental manifolds (dashed), characterized by spectral curvature $ \kappa_\ell $ and thermodynamic length $ L_\ell = \int_{\gamma} \sqrt{g_\theta(d\theta, d\theta)} $, measuring local nonlinear bending and cumulative semantic transformation, respectively ([11];[12]). Offspring lie within the convex hull of parents, indicating semantic inheritance akin to genetic recombination [13]. Distant parents yield offspring with increased curvature and length, showing semantic innovation. The offspring manifold at layer $ \ell $ is given by:

$ M^{(\ell)}_{\text{offspring}} = \alpha^{(\ell)} M^{(\ell)}_{A} + \left(1 - \alpha^{(\ell)}\right) M^{(\ell)}_{B} + \varepsilon^{(\ell)} $

where $ \alpha^{(\ell)} $ is the layer-dependent semantic dominance coefficient and $ \varepsilon^{(\ell)} $ models emergent nonlinear geometry.

References

[1] Hamming, R. W. “Error detecting and error correcting codes” Bell System Technical Journal (1950).

[2] Durbin, Richard, Eddy, Sean R, and others “Biological sequence analysis: probabilistic models of proteins and nucleic acids” arXiv preprint (1998).

[3] Pevzner, Pavel A “Computational molecular biology: an algorithmic approach” arXiv preprint (2000).

[4] Lynch, Michael “The origins of genome architecture” arXiv preprint (2007).

[5] Hamming, Richard W “Error detecting and error correcting codes” The Bell system technical journal (1950).

[6] Nei, Masatoshi “Genetic distance between populations” The American Naturalist (1972).

[7] Smith, J. M. “An analysis of the role of recombination in the evolution of bacteria” Genetics (1977).

[8] Kimura, Motoo “The Neutral Theory of Molecular Evolution” arXiv preprint (1983).

[9] Deblieck, M, Fatiukha, A, and others “GenoTypeMapper: graphical genotyping on genetic and sequence-based maps” Plant Methods (2020). https://doi.org/10.1186/s13007-020-00665-7

[10] Courbariaux, Matthieu, Bengio, Yoshua, and others “BinaryConnect: Training deep neural networks with binary weights during propagations” NeurIPS (2015).

[11] Bronstein, Michael M, Bruna, Joan, and others “Geometric deep learning: going beyond euclidean data” IEEE Signal Processing Magazine (2017).

[12] Crooks, Gavin E “Measuring thermodynamic length” Physical Review Letters (2007).

[13] Phillips, Patrick C “Epistasis—the essential role of gene interactions in the structure and evolution of genetic systems” Nature Reviews Genetics (2008).

nDNA - the Semantic Helix of Artificial Cognition