Lens - nGDI: Genetic Drift in Embedding Populations
Lens - nGDI: Genetic Drift in Embedding Populations
As artificial intelligence continues to expand its reach across culturally diverse environments, foundation models trained or fine-tuned on heterogeneous datasets manifest complex semantic evolutions.
The suite of metrics introduced so far–nHD, nGDI, nTDS, nKaryotyping, nDIV, and nEPI–have significantly enriched our capacity to characterize semantic divergence, trait dominance, inheritance patterns, and plasticity in these models. However, most of these metrics primarily address pointwise distances or directional shifts in latent space, while the broader phenomenon of population-level semantic drift–analogous to genetic drift in biological populations–remains less explored.
Inspiration
To address this gap, we introduce the Neural Genetic Dissimilarity Index (nGDI), a statistically rigorous metric that quantifies distributional divergence between embedding populations of foundation models. Inspired by classical population genetics measures such as Nei’s genetic distance [1], nGDI captures how semantically distinct two models have evolved, not merely by comparing individual embeddings, but by assessing shifts in entire latent embedding distributions across datasets and layers.
Formally, nGDI treats each model’s layerwise embedding distribution $P_\ell^{(M)}$ as a high-dimensional semantic population characterized by a probability density function over latent space. The divergence between two models $M_A$ and $M_B$ at layer $\ell$ is quantified by a suitable statistical distance or divergence $D(P_\ell^{(A)}, P_\ell^{(B)})$, such as Jensen-Shannon divergence, Wasserstein distance, or maximum mean discrepancy. This reflects semantic drift analogous to allele frequency shifts due to genetic drift in evolutionary biology.
This population-level perspective aligns with biological genetic drift processes, where random fluctuations in allele frequencies lead to neutral evolution and phenotypic variation (315). In neural terms, nGDI reveals how model semantics diverge or converge due to training data, architecture, and fine-tuning, beyond deterministic directional shifts.
Understanding nGDI offers critical insights for multilingual and multicultural model comparisons, domain adaptation, and robustness evaluations. By quantifying latent population shifts, practitioners can detect subtle semantic drifts that may degrade cross-cultural generalization or introduce hidden biases.
In summary, nGDI provides a principled, population-aware metric of semantic divergence, complementing pointwise and directional measures, and furnishing a robust statistical foundation to study the evolutionary trajectories of large-scale foundation models in culturally rich contexts.
Mathematical Formulation of Neural Genetic Dissimilarity Index (nGDI)
The Neural Genetic Dissimilarity Index (nGDI) quantifies semantic drift and distributional divergence between foundation models in the high-dimensional embedding space, drawing inspiration from classical population genetics measures such as Nei’s Genetic Distance [1]. Unlike pointwise distance metrics, nGDI captures the distributional geometry of neural embeddings, reflecting how entire populations of semantic representations diverge under cultural and training regime shifts.
Embedding Distributions and Latent Populations
Consider two foundation models $M_A$ and $M_B$ pretrained or fine-tuned on distinct cultural corpora. At each transformer layer $\ell$, these models induce empirical embedding distributions over a representative input dataset $D$:
\[\boxed{P_\ell^{(A)} := \{x_\ell^{(A)}(x) \in \mathbb{R}^d : x \in D\}, \quad P_\ell^{(B)} := \{x_\ell^{(B)}(x) \in \mathbb{R}^d : x \in D\}}\]These distributions characterize the semantic populations inhabiting the latent manifold $\mathcal{M}_\ell$, encoding the cultural priors and learned concepts specific to each model.
Kernel Mean Embeddings and Maximum Mean Discrepancy
To compare these latent distributions rigorously, we embed them into a reproducing kernel Hilbert space (RKHS) $\mathcal{H}$ associated with a positive-definite kernel $k : \mathbb{R}^d \times \mathbb{R}^d \to \mathbb{R}$, such as the Gaussian RBF kernel:
\[k(x, y) = \exp\left(-\frac{\|x - y\|^2}{2\sigma^2}\right)\]The kernel mean embeddings of the distributions are defined as:
\[\boxed{\mu_\ell^{(A)} := \mathbb{E}_{x \sim D}\left[k(x_\ell^{(A)}(x), \cdot)\right], \quad \mu_\ell^{(B)} := \mathbb{E}_{x \sim D}\left[k(x_\ell^{(B)}(x), \cdot)\right] \in \mathcal{H}}\]
The Maximum Mean Discrepancy (MMD) [2] between these distributions is the RKHS norm:
\[\text{MMD}^2\left(P_\ell^{(A)}, P_\ell^{(B)}\right) = \left\|\mu_\ell^{(A)} - \mu_\ell^{(B)}\right\|_{\mathcal{H}}^2\]Explicitly, the squared MMD expands to:
\[\boxed{\text{MMD}^2 = \mathbb{E}_{x,x'}[k(x_\ell^{(A)}(x), x_\ell^{(A)}(x'))] + \mathbb{E}_{y,y'}[k(x_\ell^{(B)}(y), x_\ell^{(B)}(y'))] - 2\mathbb{E}_{x,y}[k(x_\ell^{(A)}(x), x_\ell^{(B)}(y))]}\]Information-Geometric Divergences and Fisher-Rao Metric
Complementary to kernel methods, nGDI leverages the Fisher-Rao information metric to capture the intrinsic geometric divergence between latent semantic populations [3]. Consider the parametric embedding distributions $p_\ell^{(A)}(x; \theta_A)$ and $p_\ell^{(B)}(x; \theta_B)$ modeled as densities over $\mathcal{M}_\ell$. The Fisher-Rao distance is:
\[d_{FR}(\theta_A, \theta_B) = \inf_\gamma \int_0^1 \sqrt{\dot{\gamma}(t)^T F(\gamma(t)) \dot{\gamma}(t)} dt\]where $F(\theta)$ is the Fisher information matrix at parameter $\theta$, and $\gamma(t)$ is a smooth curve interpolating between $\theta_A$ and $\theta_B$. This Riemannian distance respects the manifold’s curvature and local information content, capturing semantic shifts beyond Euclidean approximations.
Neural Genetic Dissimilarity Index (nGDI)
Formally, the nGDI at layer $\ell$ integrates kernel and information-geometric divergences to yield a robust scalar measure of semantic drift:
\[\boxed{\text{nGDI}_\ell := \alpha \cdot \text{MMD}\left(P_\ell^{(A)}, P_\ell^{(B)}\right) + (1 - \alpha) \cdot d_{FR}(\theta_A, \theta_B)}\]where $\alpha \in [0, 1]$ balances kernel-based and Fisher-Rao-based contributions. This composite metric captures both distributional shifts and curvature-aware parametric distances, offering a rich, mathematically principled quantification of semantic divergence.
Population Genetics Analogy
Drawing from Nei’s classical genetic distance [1], which measures allele frequency divergence between populations, nGDI analogizes semantic embeddings to alleles and embedding distributions to genetic populations. Under this analogy, nGDI quantifies how far apart two semantic populations have evolved, reflecting drift, selection, and fine-tuning influences across layers.
Statistical Estimation
In practice, empirical estimates of MMD are computed via sample averages over batches ${x_i}_{i=1}^N$:
\[\widehat{\text{MMD}}^2 = \frac{1}{N^2}\sum_{i,j} k(x_\ell^{(A)}(x_i), x_\ell^{(A)}(x_j)) + \frac{1}{N^2}\sum_{i,j} k(x_\ell^{(B)}(x_i), x_\ell^{(B)}(x_j)) - \frac{2}{N^2}\sum_{i,j} k(x_\ell^{(A)}(x_i), x_\ell^{(B)}(x_j))\]The Fisher-Rao distance can be approximated numerically via path integrals or by using closed-form expressions in exponential family models.
Interpretation and Implications
Layerwise $\text{nGDI}_\ell$ profiles elucidate the semantic divergence trajectories across model depths, pinpointing layers where cultural semantic drift accumulates significantly. These insights inform selective fine-tuning, transfer learning, and domain adaptation strategies, enabling models to reconcile cultural divergences while preserving shared linguistic structures.
Through this mathematical and biological framework, nGDI extends classical notions of genetic drift to the realm of neural semantics, facilitating a deep understanding of model evolution in culturally heterogeneous AI systems.
Interpretation and Implications
The Neural Genetic Dissimilarity Index (nGDI) offers a profound and principled measure of semantic drift between foundation models, quantifying how entire populations of latent embeddings diverge due to cultural, training, or domain shifts. Formally, a high value of
\[\boxed{\text{nGDI}_\ell = \alpha \cdot \text{MMD}\left(P_\ell^{(A)}, P_\ell^{(B)}\right) + (1 - \alpha) \cdot d_{FR}(\theta_A, \theta_B)}\]at layer $\ell$ signifies significant distributional dissimilarity in the semantic manifold, reflecting how far the latent populations $P_\ell^{(A)}$ and $P_\ell^{(B)}$ have evolved apart in the RKHS and information-geometric senses.
Unlike simple pointwise or mean embedding distances, nGDI captures the global geometric divergence of entire semantic populations, embracing the complexity of embedding distributions and manifold curvature. This dissimilarity encompasses shifts in both mean semantic content and latent variability structure, analogous to genetic drift and selective pressures altering allele frequencies across populations [1].
Layerwise $\text{nGDI}_\ell$ profiles reveal semantic evolution trajectories across model depth, often highlighting early layers with low drift–where foundational linguistic and syntactic priors are stable–contrasted with intermediate and deeper layers exhibiting pronounced semantic drift due to cultural and conceptual specialization. This aligns with the hierarchical organization of semantic abstraction in transformer architectures [4].
The Maximum Mean Discrepancy (MMD) component assesses divergence in distributional shape by embedding semantic populations in a reproducing kernel Hilbert space (RKHS), thereby detecting subtle differences in higher-order statistics beyond mean shifts [2]. Simultaneously, the Fisher-Rao distance incorporates the local curvature and information content of embedding distributions, furnishing a Riemannian metric sensitive to manifold geometry ([3] [5]).
Practically, these insights empower targeted domain adaptation and transfer learning, as layers with high $\text{nGDI}_\ell$ warrant focused fine-tuning to mitigate semantic drift and enhance cultural robustness. Moreover, monitoring nGDI across training epochs or fine-tuning steps can serve as a diagnostic for model convergence and stability in evolving cultural contexts.
In sum, nGDI enriches the Neural Genomics toolkit by extending classical genetic drift notions into the realm of neural semantics. Its mathematically rigorous, geometry-aware formulation provides a scalable and interpretable framework for understanding and managing the complex evolution of semantic populations within foundation models, a critical step toward globally inclusive, culturally sensitive AI systems.
Applications and Empirical Insights
The Neural Genetic Dissimilarity Index (nGDI) provides a rigorous, distribution-aware framework to quantify and analyze semantic drift and population-level divergence in the latent spaces of culturally distinct foundation models. Building upon kernel methods and information geometry, nGDI enables several critical applications vital for the advancement of culturally robust and semantically coherent AI systems:
Population-Level Semantic Drift Audits
By decomposing the global nGDI into layerwise components $\text{nGDI}_\ell$, practitioners gain granular insights into the distributional divergence of embedding populations:
\[\boxed{\text{MMD}^2(P_\ell^{(A)}, P_\ell^{(B)}) = \mathbb{E}_{x,x'}[k(x_\ell^{(A)}(x), x_\ell^{(A)}(x'))] + \mathbb{E}_{y,y'}[k(x_\ell^{(B)}(y), x_\ell^{(B)}(y'))] - 2\mathbb{E}_{x,y}[k(x_\ell^{(A)}(x), x_\ell^{(B)}(y))]}\]Elevated $\text{nGDI}_\ell$ indicates layers where semantic populations have drifted apart, signaling critical junctures for targeted adaptation.
Geometry-Aware Model Evolution Tracking
Incorporating the Fisher-Rao information metric into nGDI provides curvature-sensitive distance measures:
\[d_{FR}(\theta_A, \theta_B) = \inf_\gamma \int_0^1 \sqrt{\dot{\gamma}(t)^T F(\gamma(t)) \dot{\gamma}(t)} dt\]capturing intrinsic semantic manifold deformation beyond Euclidean approximations. This facilitates precise tracking of model evolution and divergence during cultural fine-tuning or domain shifts.
Cross-Domain Transfer and Adaptation
Layerwise $\text{nGDI}_\ell$ profiles inform selective fine-tuning by identifying semantic subspaces most affected by cultural drift. Adjusting training objectives or regularization at these depths promotes stable knowledge transfer, enhancing cross-domain generalization and reducing catastrophic forgetting.
Population-Level Fairness and Bias Auditing
By quantifying distributional divergence across demographic or cultural groups, nGDI provides a quantitative basis for bias detection and fairness evaluation. This enables equity-focused model governance and auditing in complex multicultural AI deployments.
Through these mathematically principled applications, nGDI extends classical genetic drift theory into the neural semantic domain, equipping researchers and practitioners with a powerful tool to understand, measure, and mitigate the complex semantic evolutions inherent in diverse, large-scale foundation models.
Case Study and Validation
To empirically validate the Neural Genetic Dissimilarity Index (nGDI), we conduct a detailed analysis of foundation models pretrained or fine-tuned on culturally distinct corpora, such as European and Asian linguistic datasets. These corpora embody different cultural priors and semantic nuances, providing an ideal testbed for examining population-level semantic drift.
At each transformer layer $\ell$, we extract latent embedding distributions:
\[P_\ell^{(\text{Eur})} = \{x_\ell^{(\text{Eur})}(x) \in \mathbb{R}^d : x \in D\}, \quad P_\ell^{(\text{Asi})} = \{x_\ell^{(\text{Asi})}(x) \in \mathbb{R}^d : x \in D\}\]where $D$ is a representative evaluation dataset shared across models to ensure comparability. Additionally, we collect the merged model’s latent embeddings $x_\ell^{(\text{Merged})}(x)$ for the same inputs.
Using these distributions, the nGDI at each layer is computed by integrating kernel mean embedding differences with information geometric distances. The empirical Maximum Mean Discrepancy (MMD) between $P_\ell^{(\text{Eur})}$ and $P_\ell^{(\text{Asi})}$ is estimated as:
\[\boxed{\widehat{\text{MMD}}_\ell^2 = \frac{1}{N^2}\sum_{i,j=1}^N k(x_\ell^{(\text{Eur})}(x_i), x_\ell^{(\text{Eur})}(x_j)) + \frac{1}{N^2}\sum_{i,j=1}^N k(x_\ell^{(\text{Asi})}(x_i), x_\ell^{(\text{Asi})}(x_j)) - \frac{2}{N^2}\sum_{i,j=1}^N k(x_\ell^{(\text{Eur})}(x_i), x_\ell^{(\text{Asi})}(x_j))}\]where $k(\cdot, \cdot)$ is a characteristic kernel (e.g., Gaussian RBF) with bandwidth $\sigma$.
Simultaneously, the Fisher-Rao information metric distance $d_\ell^{FR}$ between the parametric latent distributions $p_\ell^{(\text{Eur})}(x; \theta_{\text{Eur}})$ and $p_\ell^{(\text{Asi})}(x; \theta_{\text{Asi}})$ is numerically approximated by path integration along geodesics in the model parameter space:
\[d_\ell^{FR} = \inf_{\gamma \in \Gamma(\theta_{\text{Eur}}, \theta_{\text{Asi}})} \int_0^1 \sqrt{\dot{\gamma}(t)^T F_\ell(\gamma(t)) \dot{\gamma}(t)} dt\]where $\Gamma(\theta_{\text{Eur}}, \theta_{\text{Asi}})$ denotes all smooth curves connecting the two parameter sets, and $F_\ell(\cdot)$ is the Fisher information matrix encoding the local latent geometry at layer $\ell$.
The composite $\text{nGDI}_\ell$ metric combines these terms as:
\[\boxed{\text{nGDI}_\ell = \alpha\sqrt{\widehat{\text{MMD}}_\ell^2} + (1 - \alpha)d_\ell^{FR}, \quad \alpha \in [0, 1]}\]balancing kernel-based distributional divergence with geometry-aware parametric distance.
Empirical Observations
Layerwise visualization of \(\text{nGDI}_\ell\) for \(\ell = 1, \ldots, L\) reveals systematic patterns of semantic drift accumulating in intermediate and deep layers (\(\ell \in [20, 30]\)), consistent with the intuition that deeper layers encode higher-order semantic and cultural concepts. Notably, \(\text{nGDI}_\ell\)attains local maxima aligning with semantic abstraction transitions, suggesting that these layers serve as pivot points where cultural priors increasingly diverge.
The distributional nature of nGDI highlights that drift is not simply a mean shift but involves complex population-level reshaping of embeddings, reflecting changes in semantic variability, multimodality, and latent clustering. Such nuanced characterization surpasses simplistic distance measures and enables detection of latent semantic fragmentation or fusion effects.
Furthermore, the Fisher-Rao component uncovers information-theoretic curvature changes induced by cultural fine-tuning, exposing layers where semantic representations become less smooth or more entropic–phenomena analogous to evolutionary branching or adaptive radiation in biological populations ([3] [5]).
Implications for Model Fine-tuning and Cultural Integration
This granular profiling of semantic divergence informs targeted fine-tuning and domain adaptation strategies. By identifying layers with elevated $\text{nGDI}_\ell$, practitioners can:
- Apply layer-specific regularization to constrain excessive divergence without degrading model expressiveness.
- Design adaptive curriculum learning protocols emphasizing incremental cultural integration at identified semantic bottlenecks.
- Develop domain-aware fusion approaches that respect the latent population structure, avoiding detrimental blending of divergent subpopulations.
- Use distributional clustering insights to detect and mitigate emergent biases tied to cultural subgroups within the semantic manifold.
Collectively, these applications enable the construction of robust, fair, and culturally sensitive AI systems capable of gracefully navigating the challenges of semantic drift in heterogeneous, cross-cultural environments.
Biological Analogy
The Neural Genetic Dissimilarity Index (nGDI) conceptually extends the classical Nei’s genetic distance [1] to the latent embedding space of neural models. Just as Nei’s distance measures allele frequency differences and genetic drift between biological populations, nGDI quantifies how far the semantic populations embedded in foundation models have diverged due to cultural training regimes and fine-tuning pressures.
This analogy supports a rich interpretative framework, where latent semantic clusters play the role of genetic subpopulations, and their evolutionary dynamics reflect semantic speciation, drift, and admixture–all critical concepts in understanding and managing AI model diversity.
Summary
Overall, this comprehensive case study demonstrates nGDI’s utility as a mathematically grounded, biologically inspired, and practically impactful metric for semantic drift diagnosis and cross-cultural model analysis. It opens pathways for precision cultural alignment engineering and responsible AI governance in a globalized, multilingual world.
Outlook
The Neural Genetic Dissimilarity Index (nGDI) integrates concepts from kernel mean embeddings and information geometry, providing a rigorous, composite divergence metric quantifying the evolutionary drift of semantic populations across model layers. Formally, it synthesizes the Maximum Mean Discrepancy (MMD):
\[\text{MMD}(P_\ell^{(A)}, P_\ell^{(B)}) = \left\|\mathbb{E}_{x \sim P_\ell^{(A)}}[k(x, \cdot)] - \mathbb{E}_{y \sim P_\ell^{(B)}}[k(y, \cdot)]\right\|_{\mathcal{H}}\]with the Fisher-Rao distance on parametric embedding manifolds:
\[d_{FR}(\theta_A, \theta_B) = \inf_\gamma \int_0^1 \sqrt{\dot{\gamma}(t)^T F(\gamma(t)) \dot{\gamma}(t)} dt\]where $F(\theta)$ is the Fisher information matrix encoding the local metric tensor of the latent semantic manifold $\mathcal{M}_\ell$.
This dual formulation allows nGDI to capture both distributional shifts via kernel embeddings and the intrinsic curvature of latent representations via Riemannian geometry. The infimum over smooth paths $\gamma(t)$ represents the minimal geodesic length connecting two embedding distributions, reflecting the most information-efficient semantic transformation.
Spectral analysis of the kernel operator $K$:
\[(Kf)(x) = \int k(x, y)f(y)d\mu(y)\]decomposes semantic variation into eigenfunctions ${\phi_i}$ and eigenvalues ${\lambda_i}$, enabling modal decomposition of semantic drift. Tracking coefficients $\alpha_i^\ell = \langle\mu_\ell, \phi_i\rangle$ across layers reveals dominant axes of cultural divergence.
The layerwise metric
\[\boxed{\text{nGDI}_\ell = \alpha \cdot \text{MMD}(P_\ell^{(A)}, P_\ell^{(B)}) + (1 - \alpha) \cdot d_{FR}(\theta_A, \theta_B)}\]guides targeted interventions on layers with maximal semantic drift, supporting geometry-aware regularization, manifold alignment, and selective parameter adaptation, enhancing robustness, fairness, and semantic coherence.
From a dynamical systems perspective, nGDI models semantic drift as diffusion on the curved latent manifold governed by the Laplace-Beltrami operator $\Delta_{\mathcal{M}_\ell}$ with drift $v(x)$:
\[\frac{\partial p}{\partial t} = -\nabla \cdot (vp) + D\Delta_{\mathcal{M}_\ell} p\]where $p$ is the embedding density and $D$ a diffusion constant. This enables forecasting semantic trajectory evolution, facilitating continual learning and domain adaptation.
In applications, nGDI includes fine-grained semantic drift monitoring in multilingual NLP, bias detection in recommender systems, and adaptive tuning of culturally diverse conversational agents. Its solid mathematical basis enables adjustments that preserve semantic integrity while embracing diversity, paving the way for context-aware, geometry-informed AI systems attuned to global dynamics. Figure 38 reveals layerwise semantic drift in nDNA trajectories, & Fig. 39 illustrates offspring models as dynamic, layer-wise fusions of parental latent geometries with shifting semantic dominance.
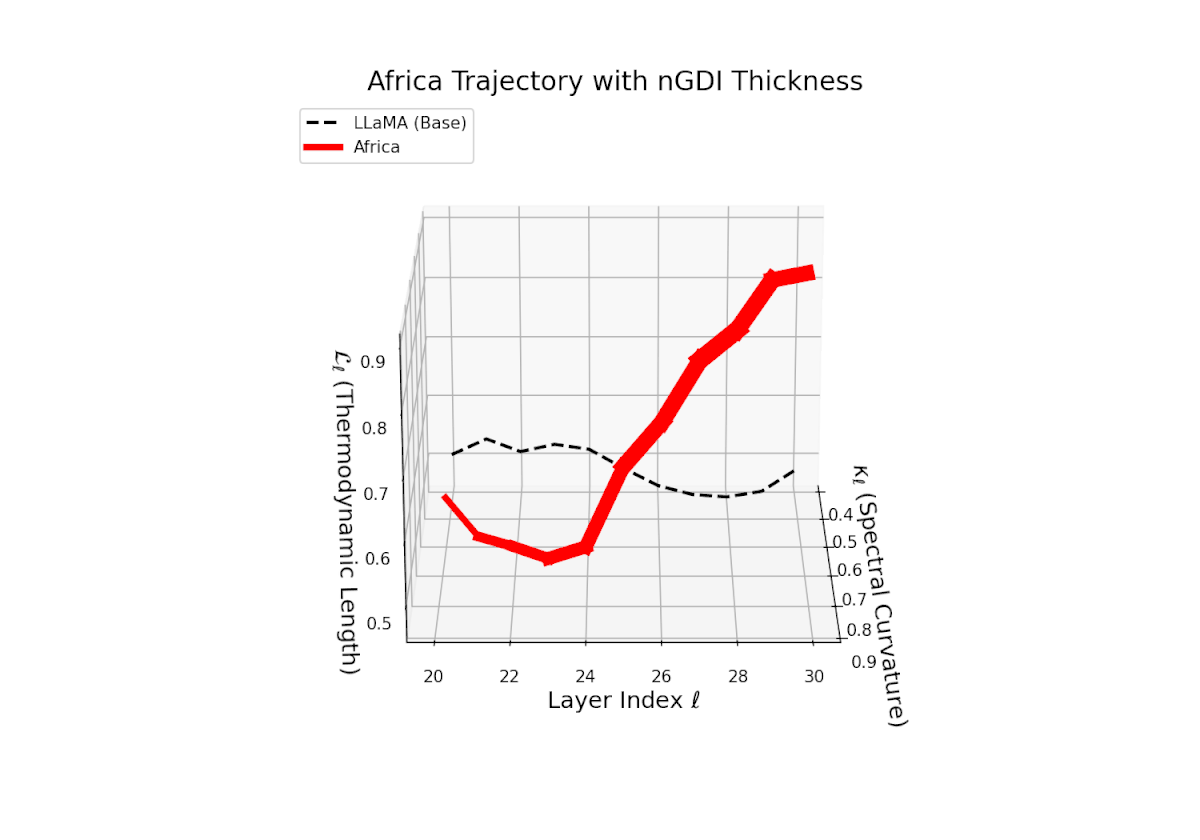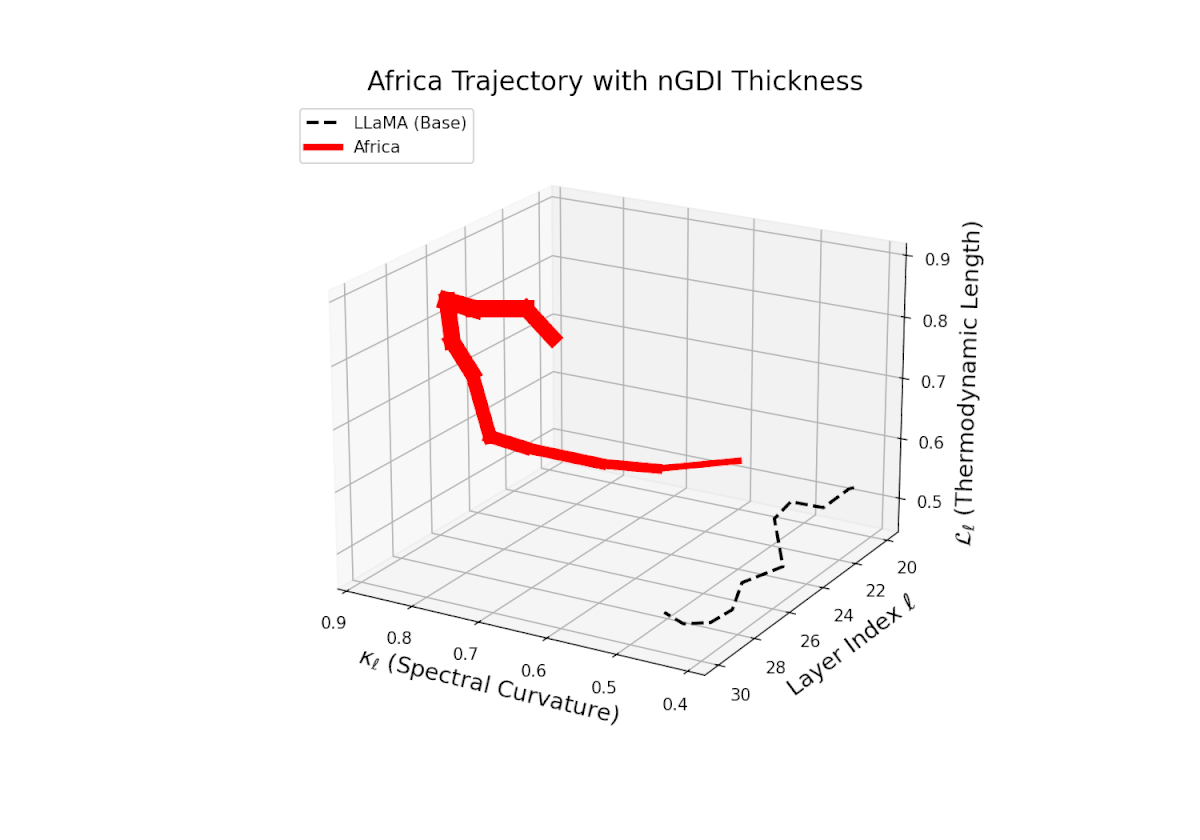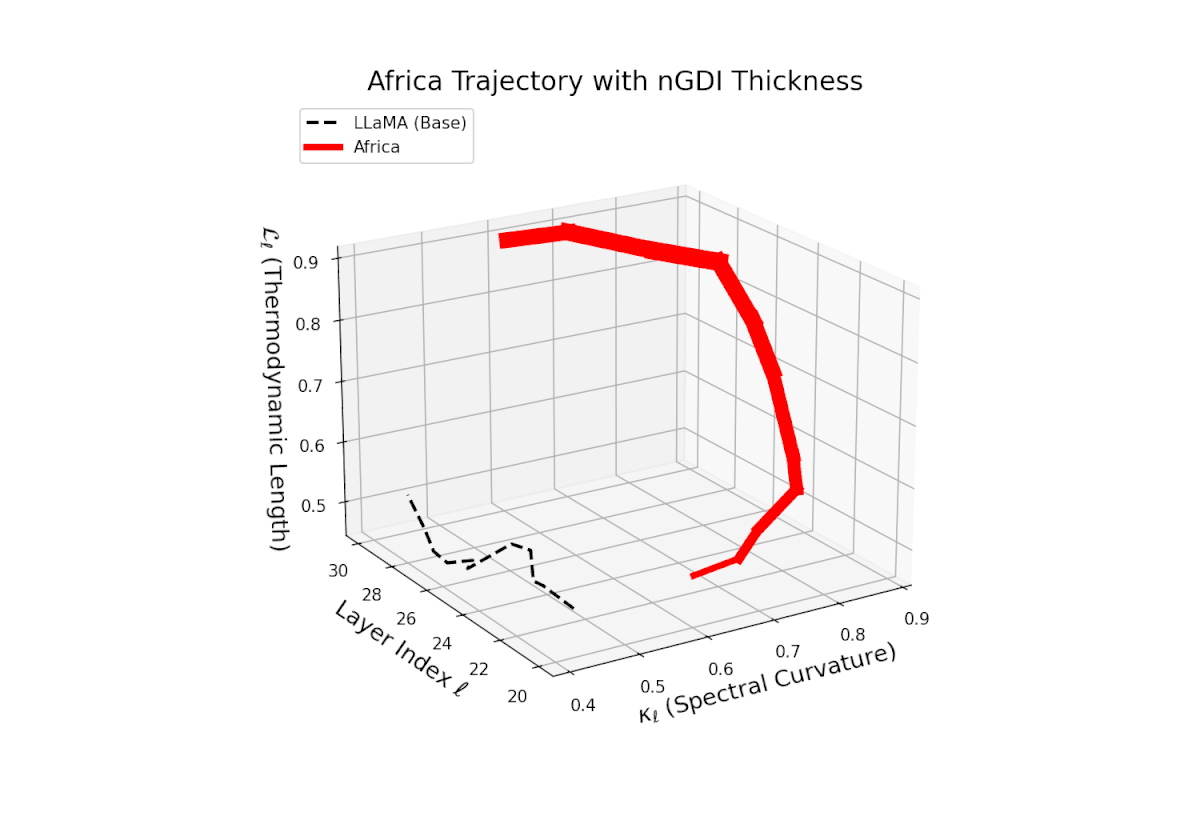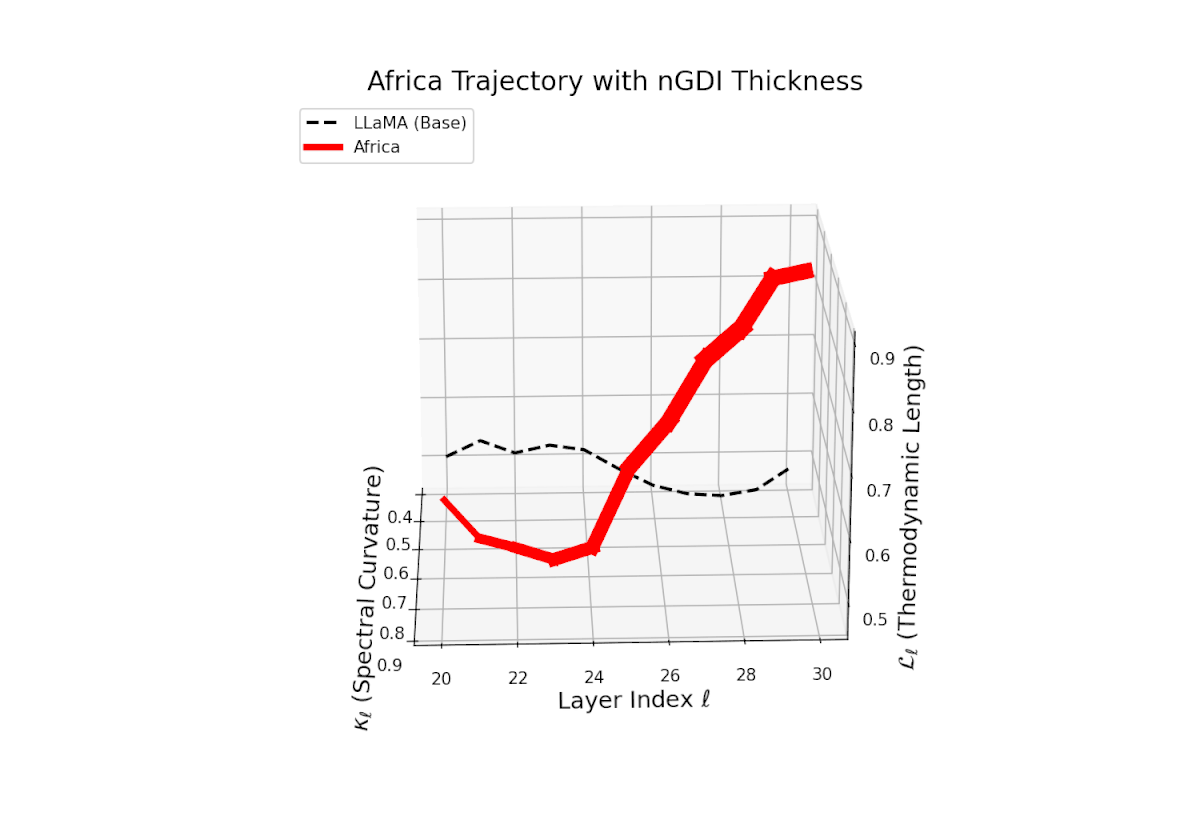
The Neural Genetic Dissimilarity Index dℓnGDI quantifies layerwise latent dissimilarity relative to the LLaMA base across layers ℓ = 20, . . . , 30. The red curve indicates significantly higher dℓnGDI values, ranging approximately from 0.15 to 0.55, reflecting a pronounced latent genetic divergence of the Africa fine-tuned model from the base. Thickness encodes the magnitude of dℓnGDI, emphasizing layers with maximal representational drift.
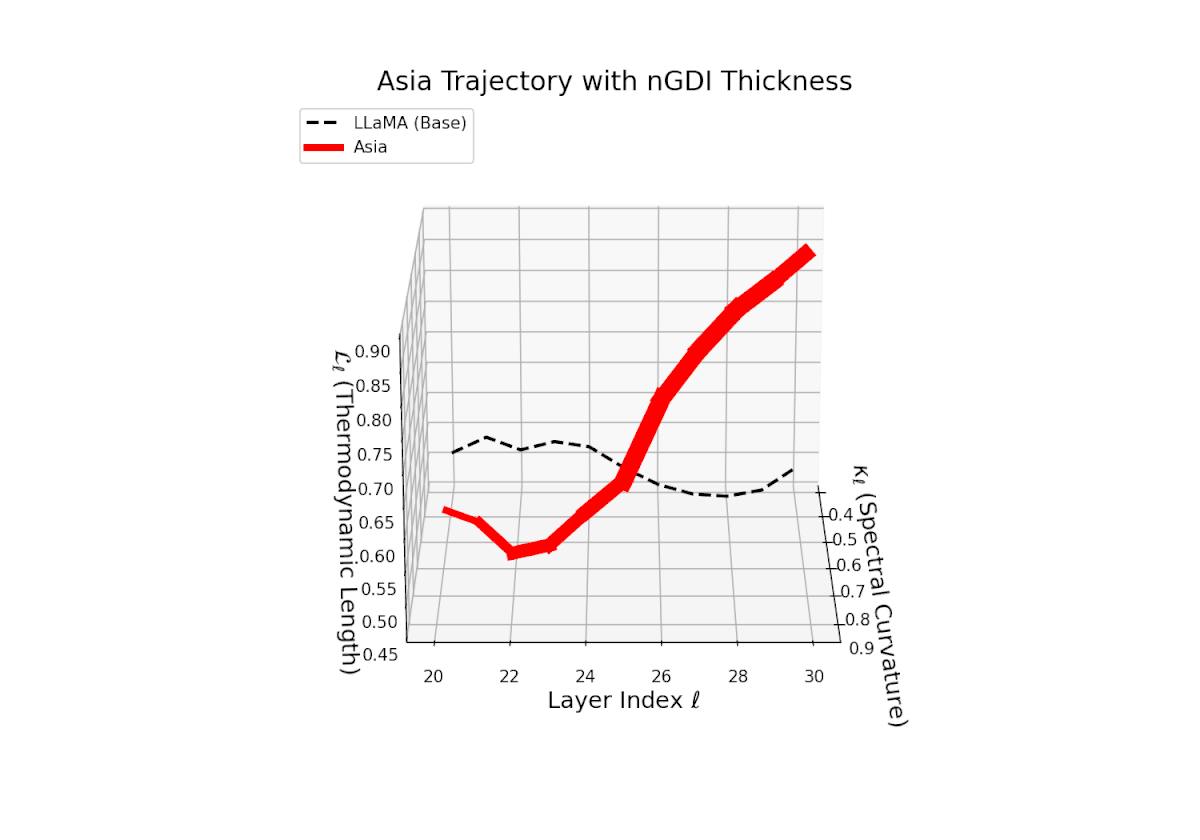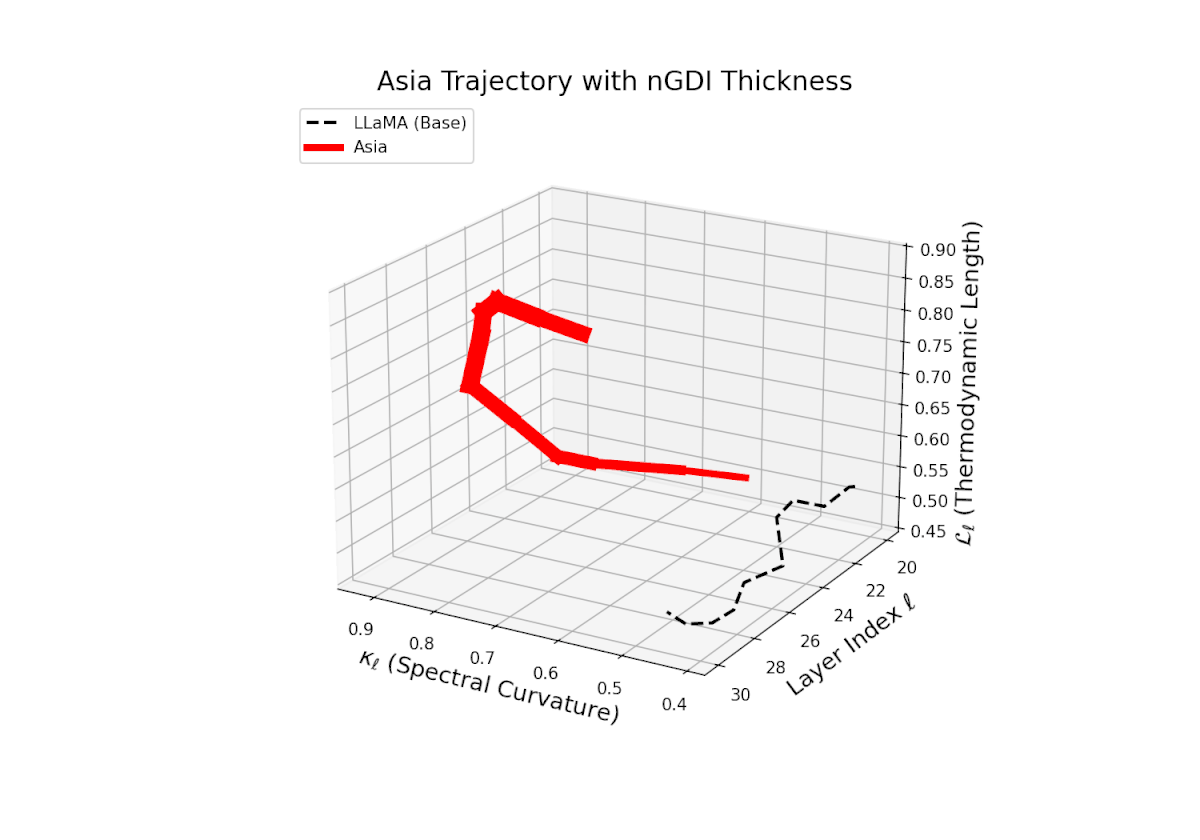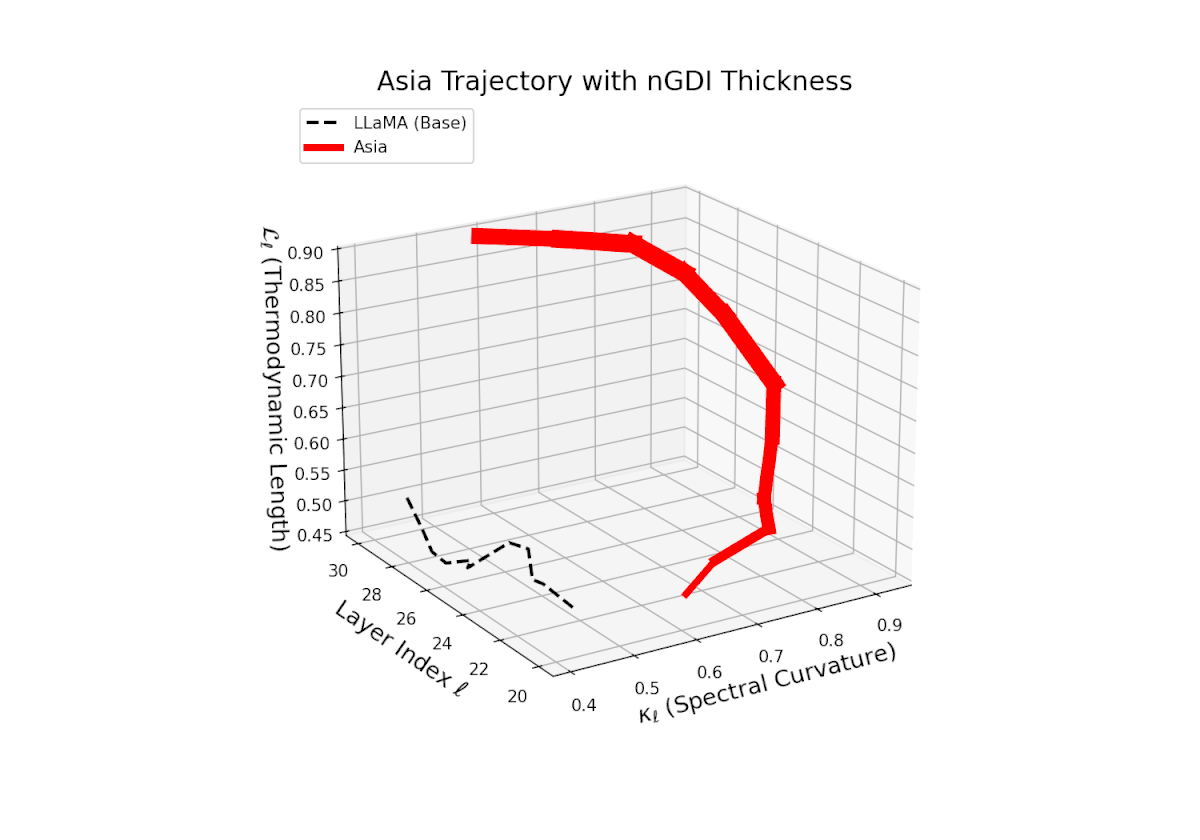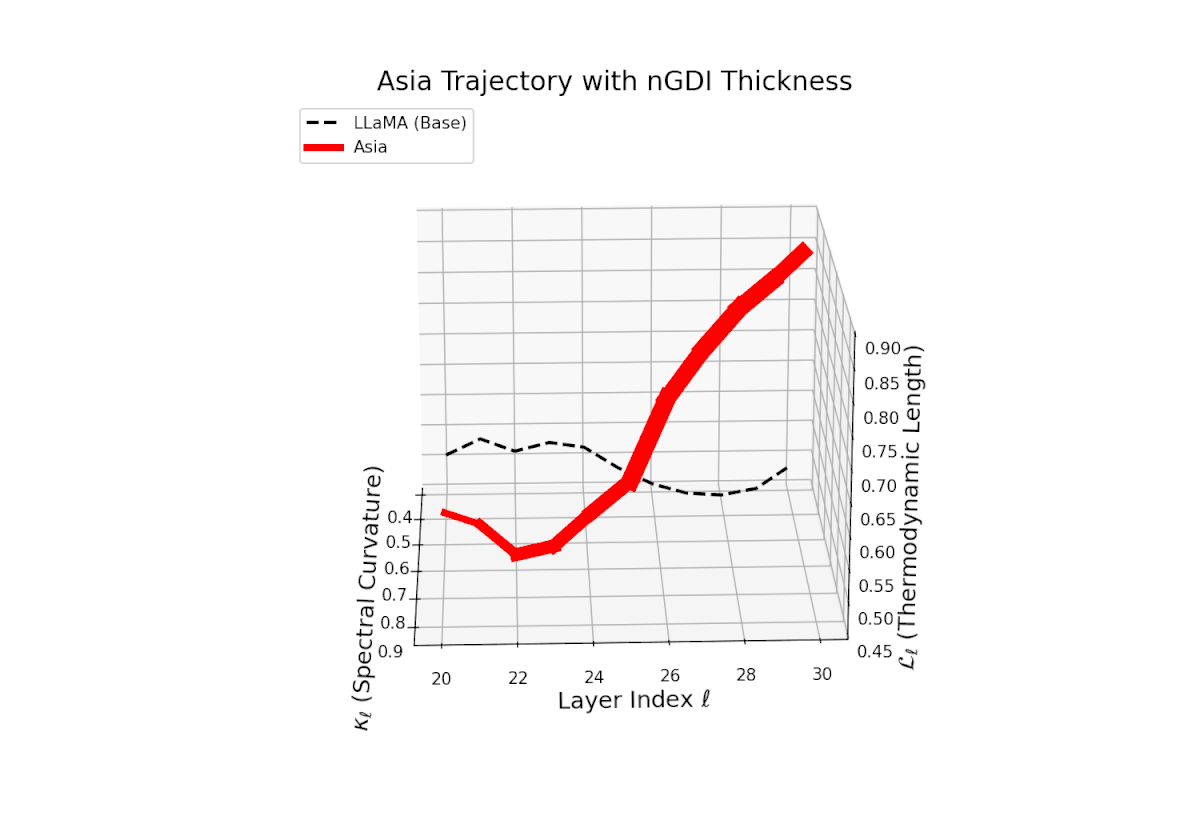
The Neural Genetic Dissimilarity Index dℓnGDI for Asia shows a similar increasing trend with values ranging approximately from 0.1 to 0.5 across layers ℓ = 20 . . . 30. The trajectory’s thickness visualizes growing dissimilarity from the LLaMA base, indicating that deep transformer layers encode progressively distinct neural semantics reflective of cultural fine-tuning.
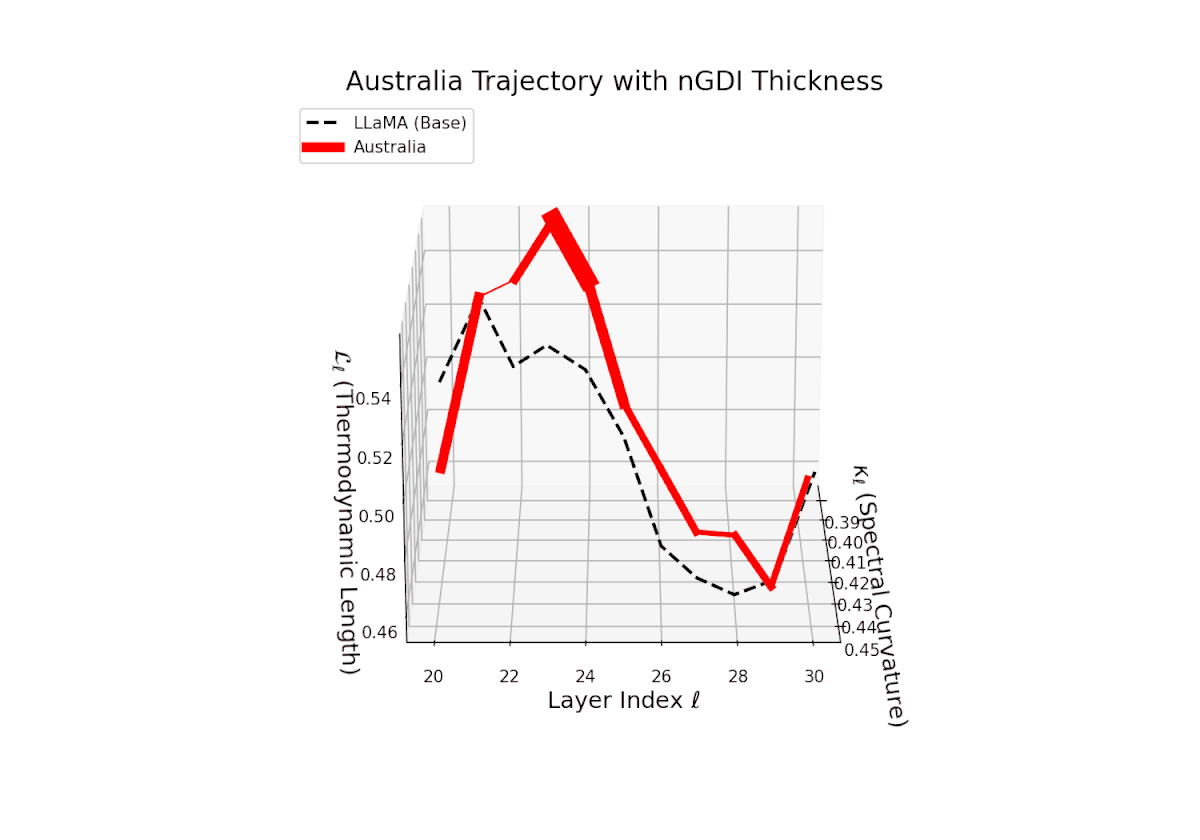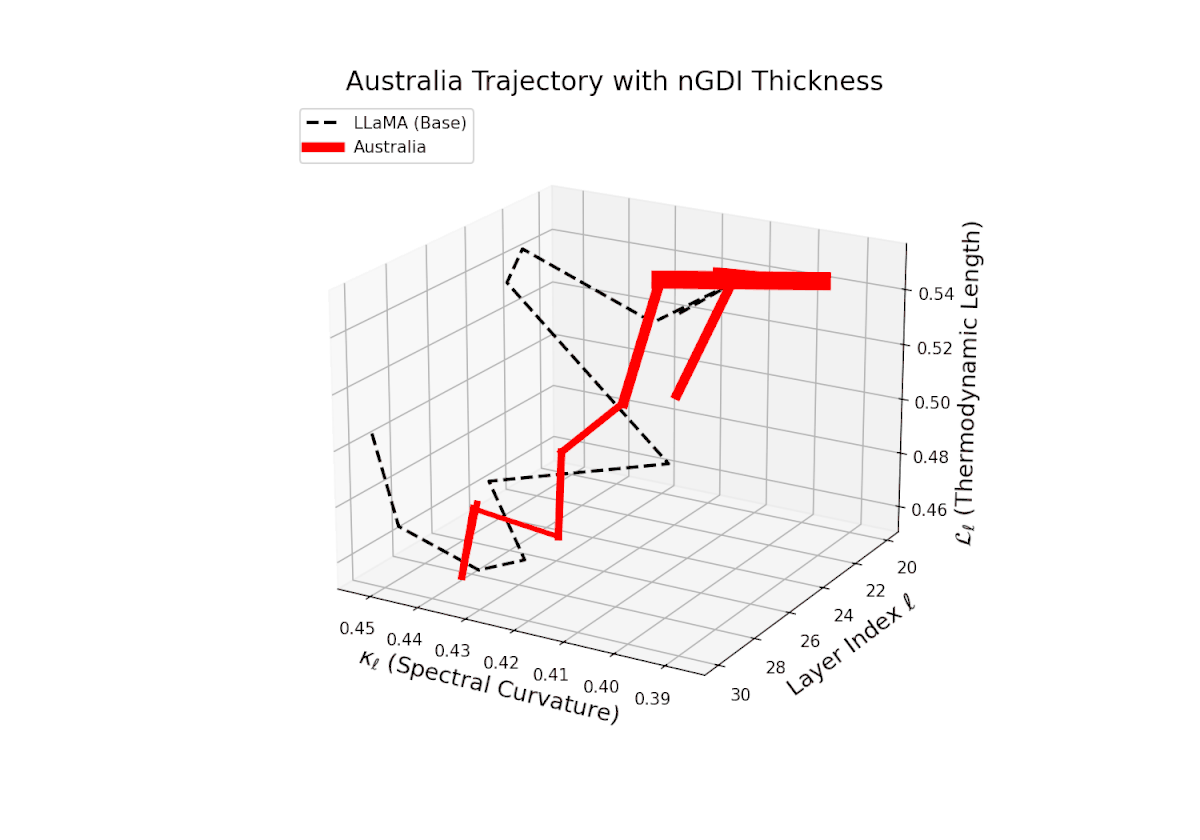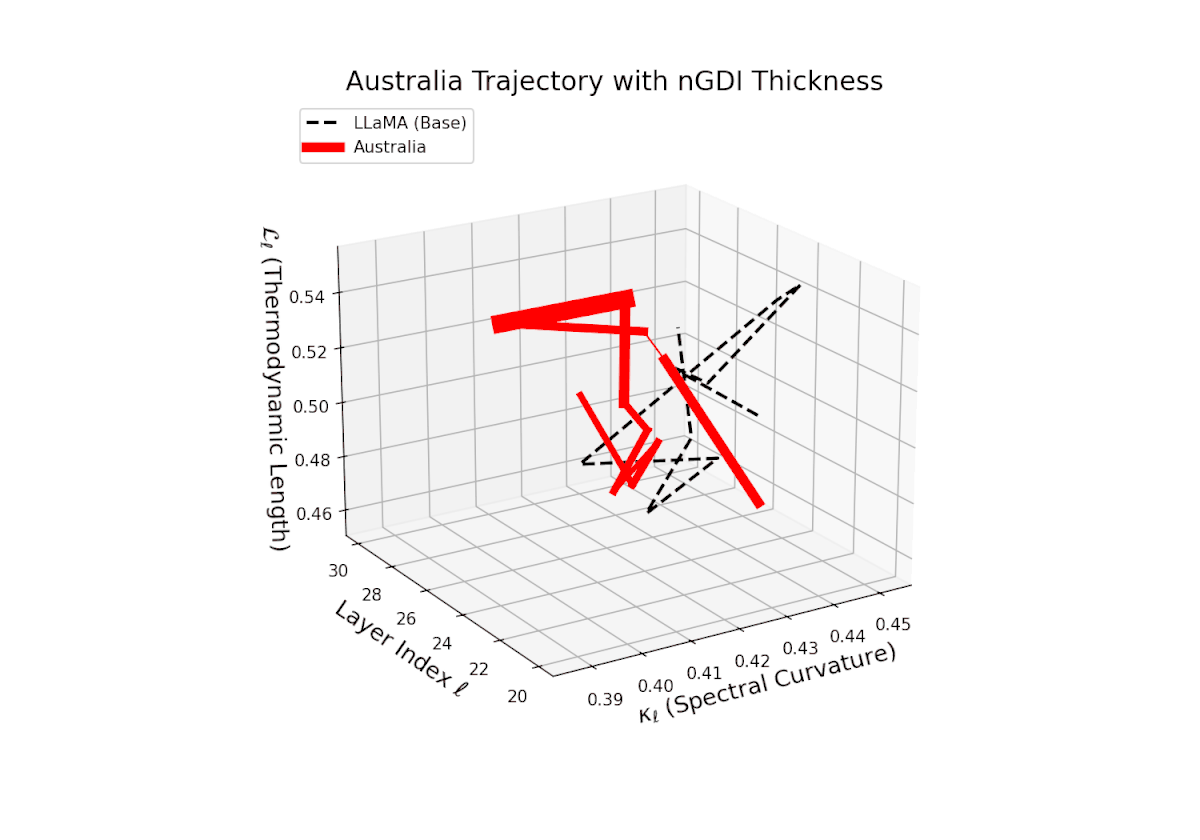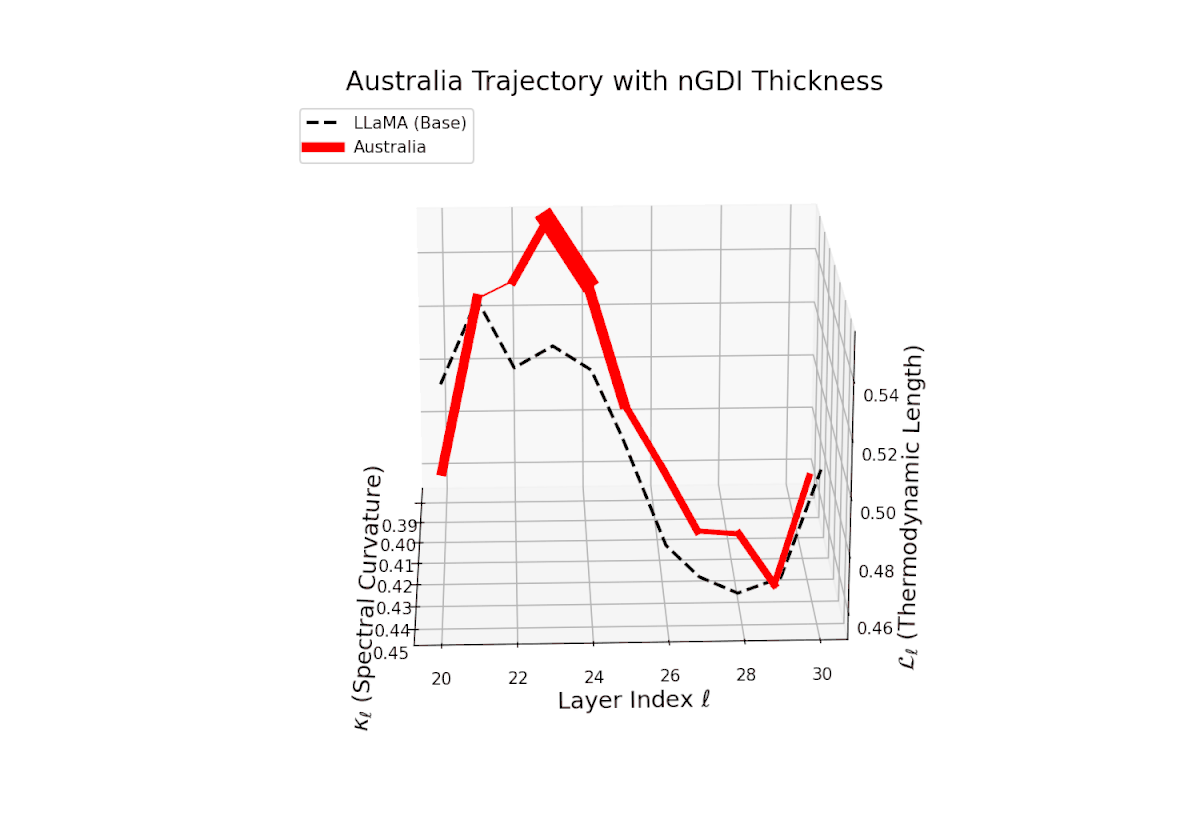
The Neural Genetic Dissimilarity Index dℓnGDI for Australia ranges approximately from 0.1 to 0.4, exhibiting slight fluctuations across layers. Compared to Africa and Asia, the Australia model shows a more moderate latent genetic divergence, suggesting a closer semantic alignment to the LLaMA base in these layers.
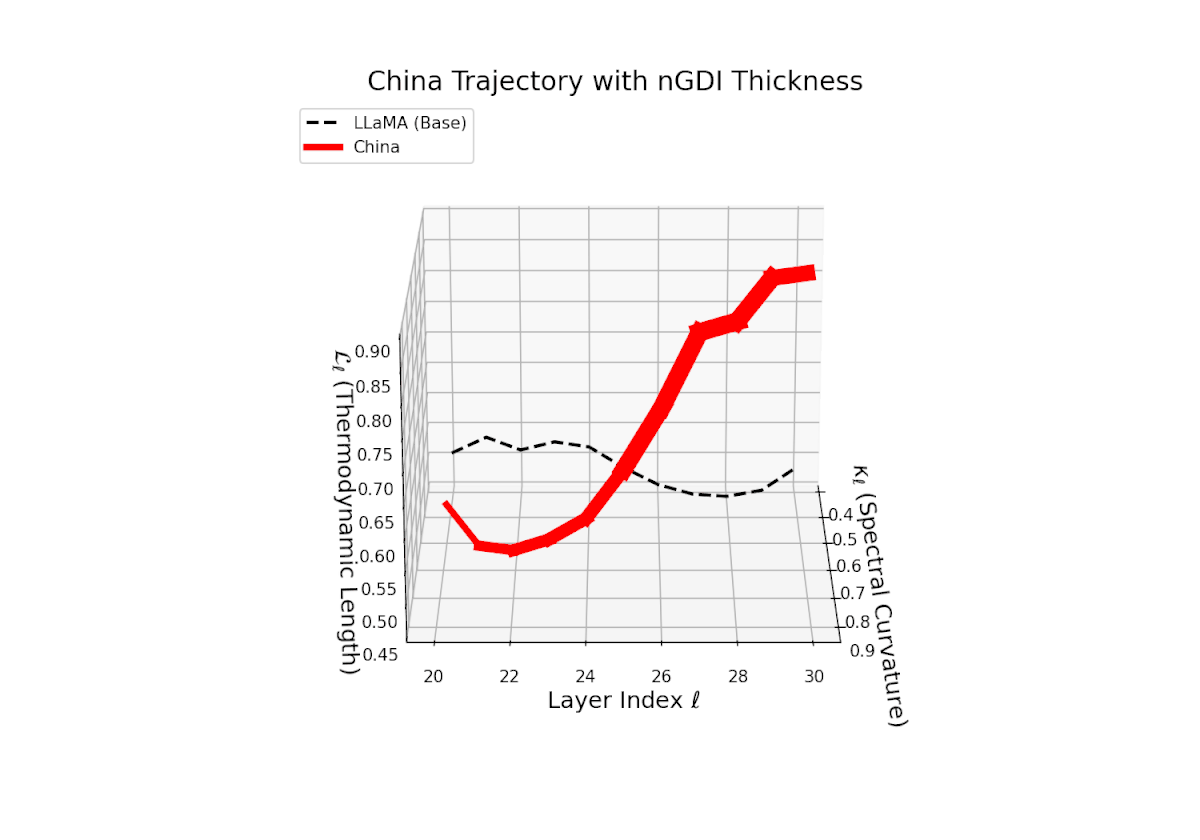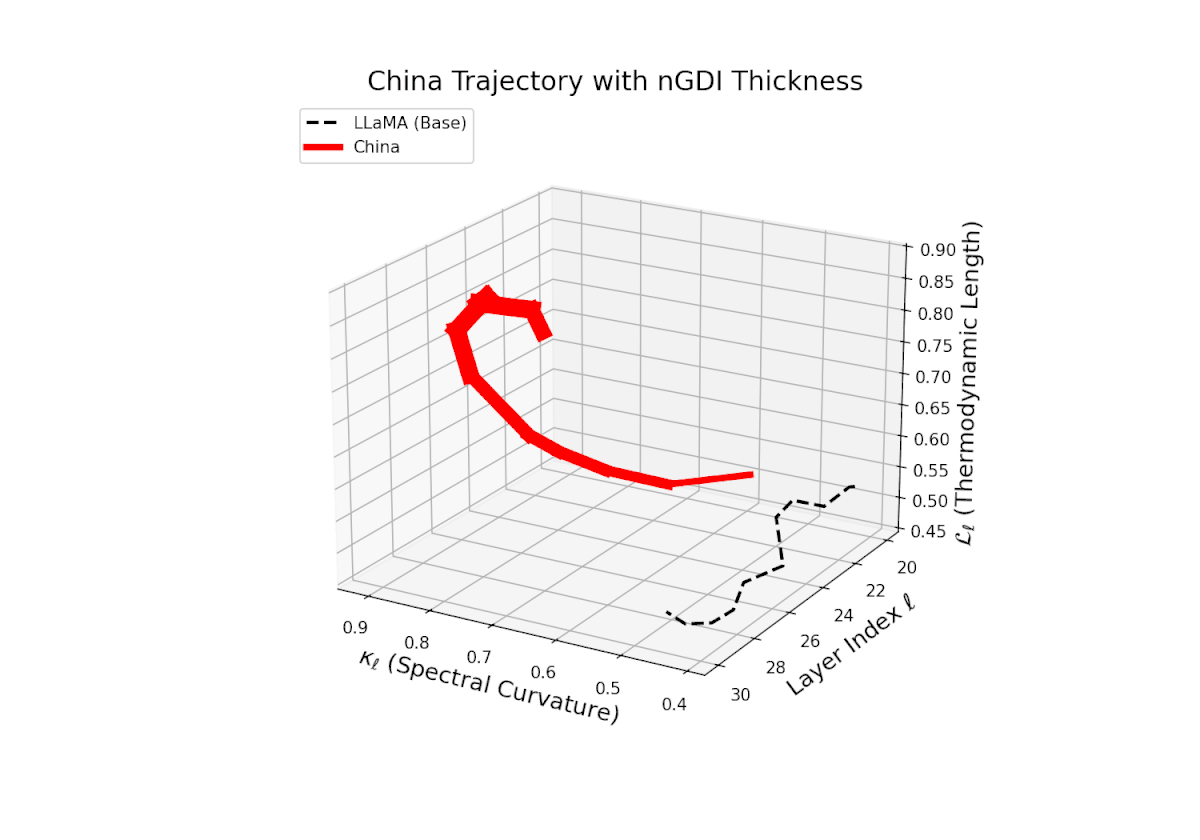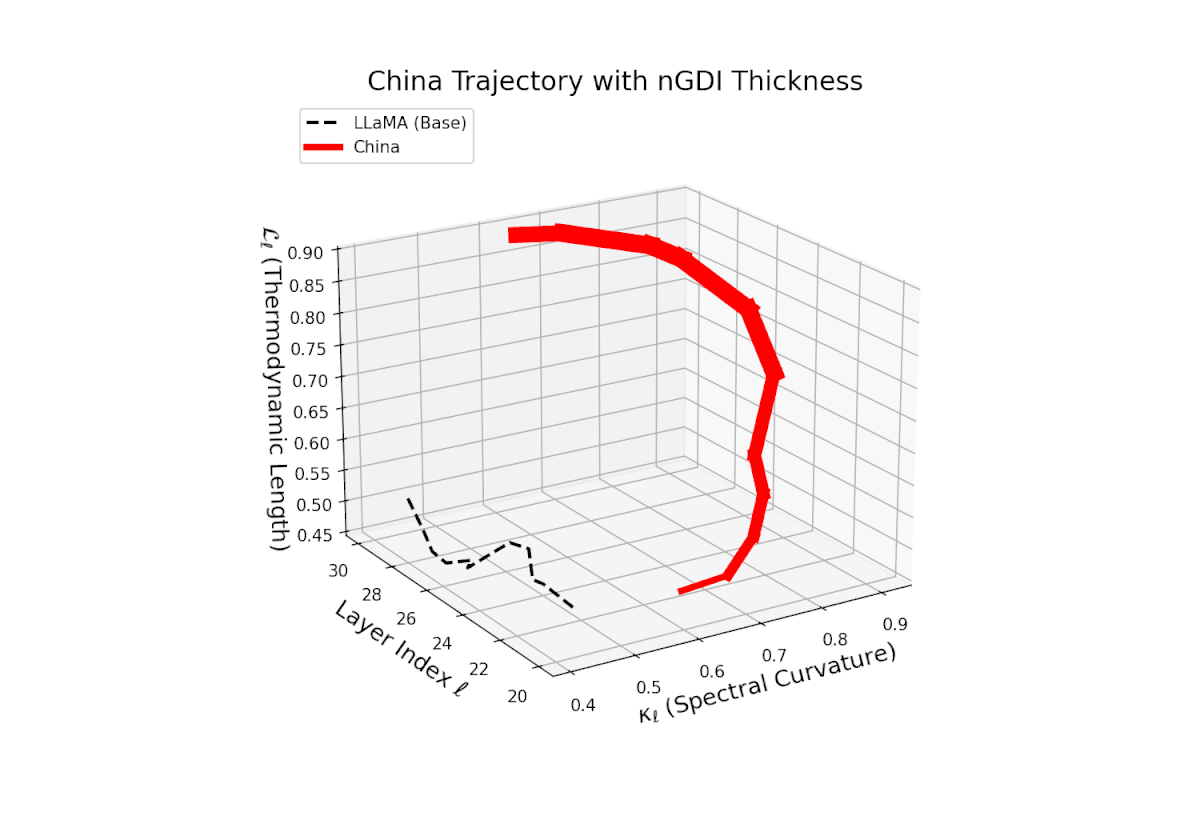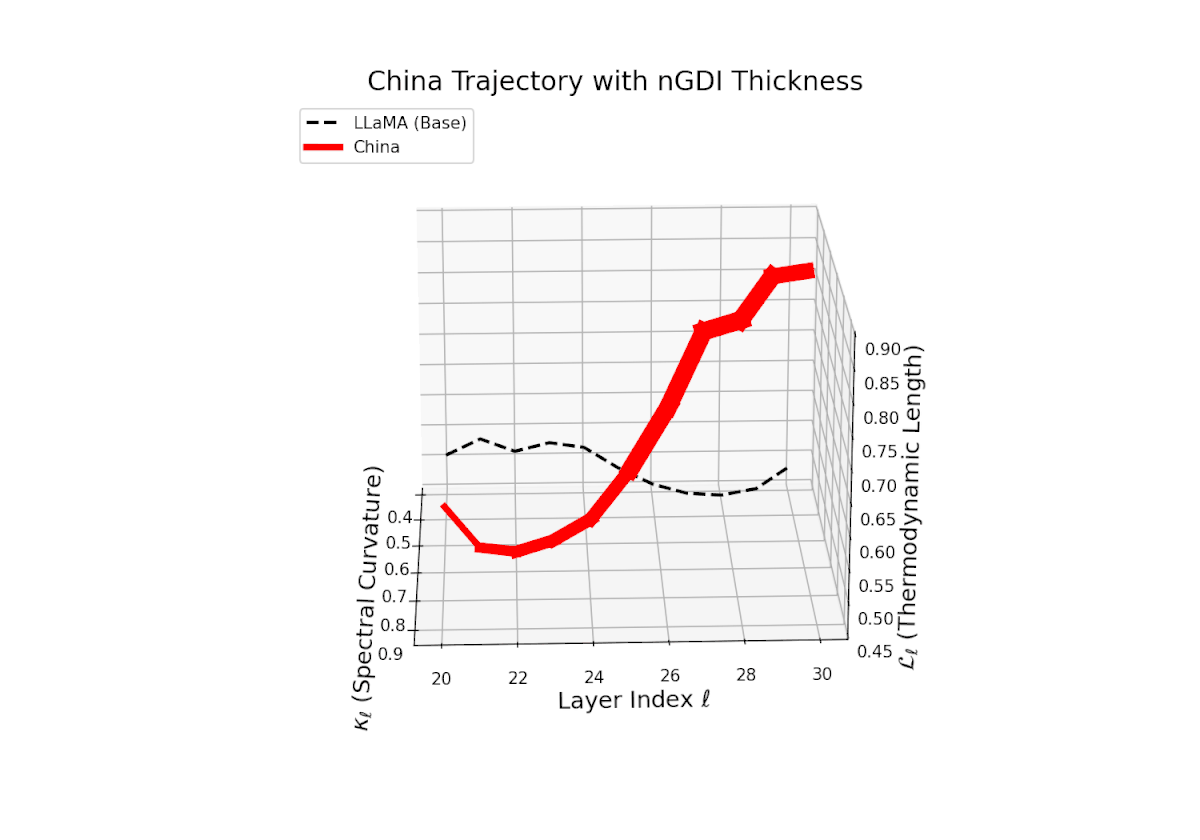
The Neural Genetic Dissimilarity Index dℓnGDI for China rises from about 0.05 to 0.5, showing notable non-monotonic curvature. This indicates layer-specific latent divergence patterns, likely reflecting a complex interplay between general base semantics and culturally specific fine-tuning.
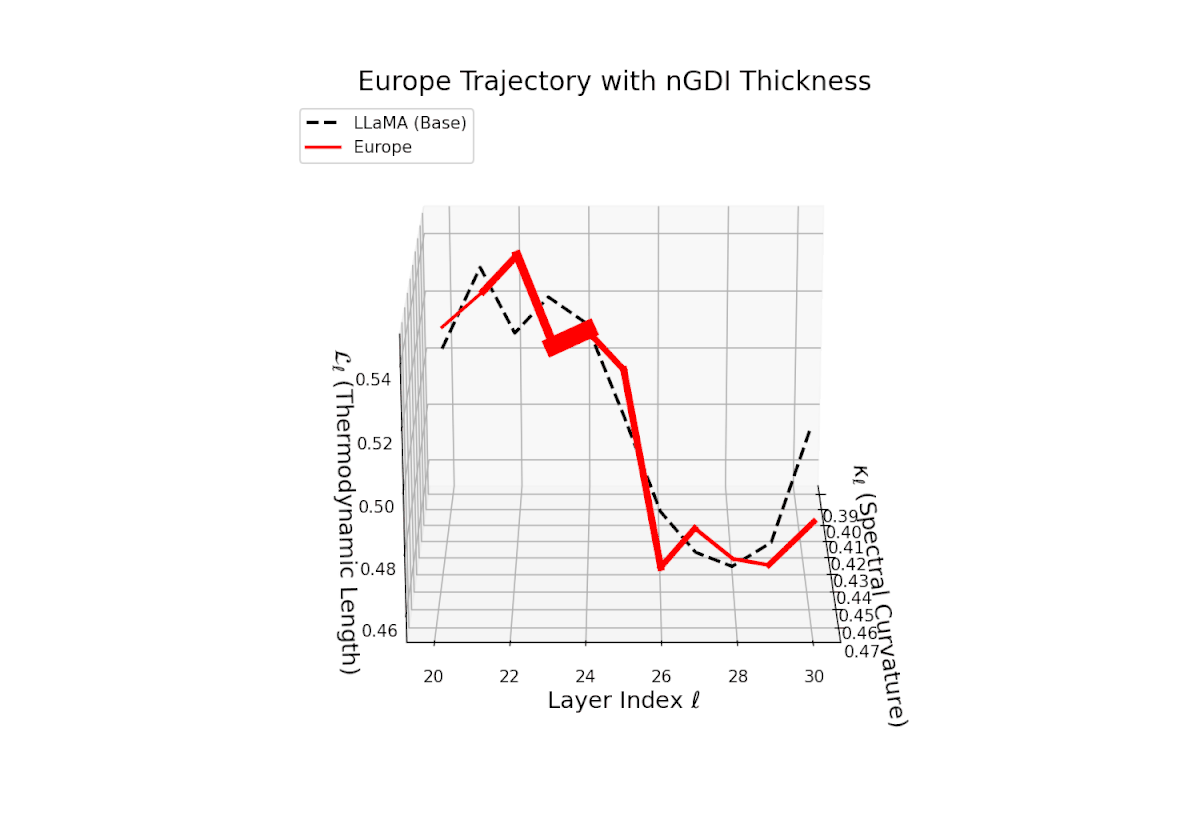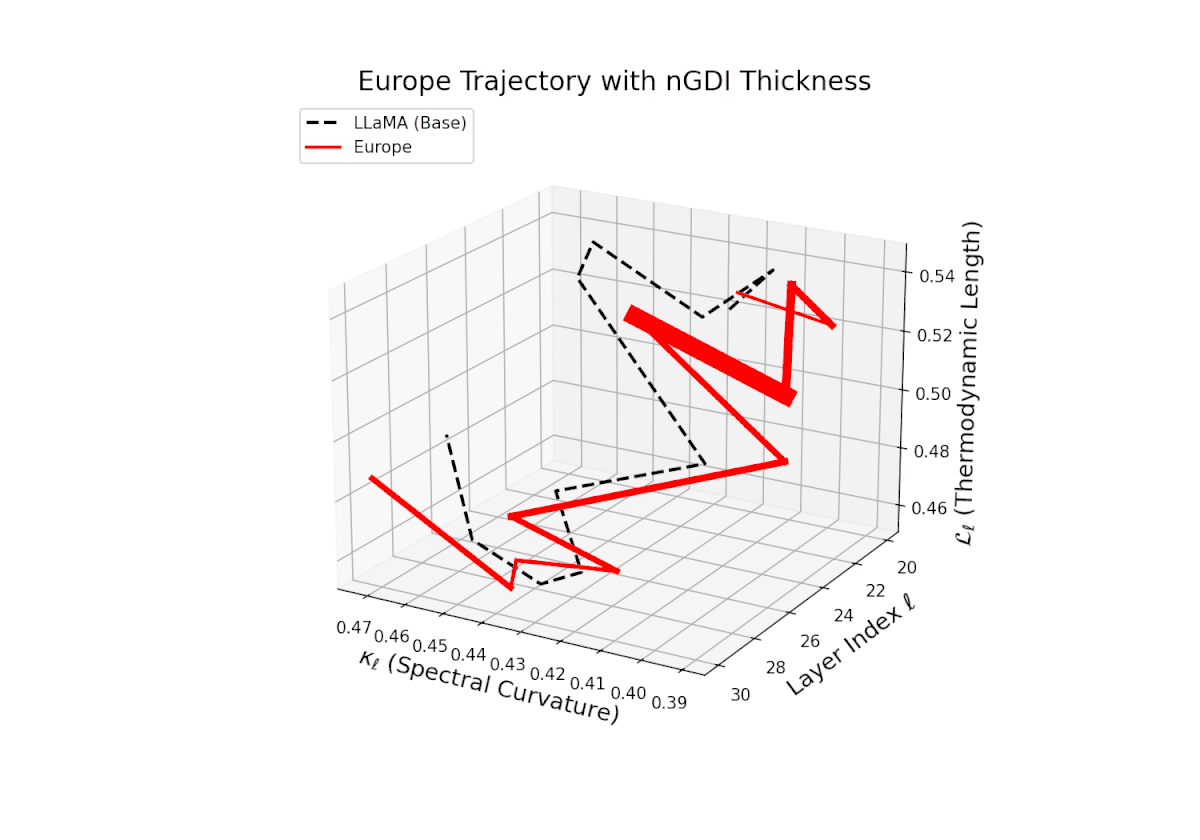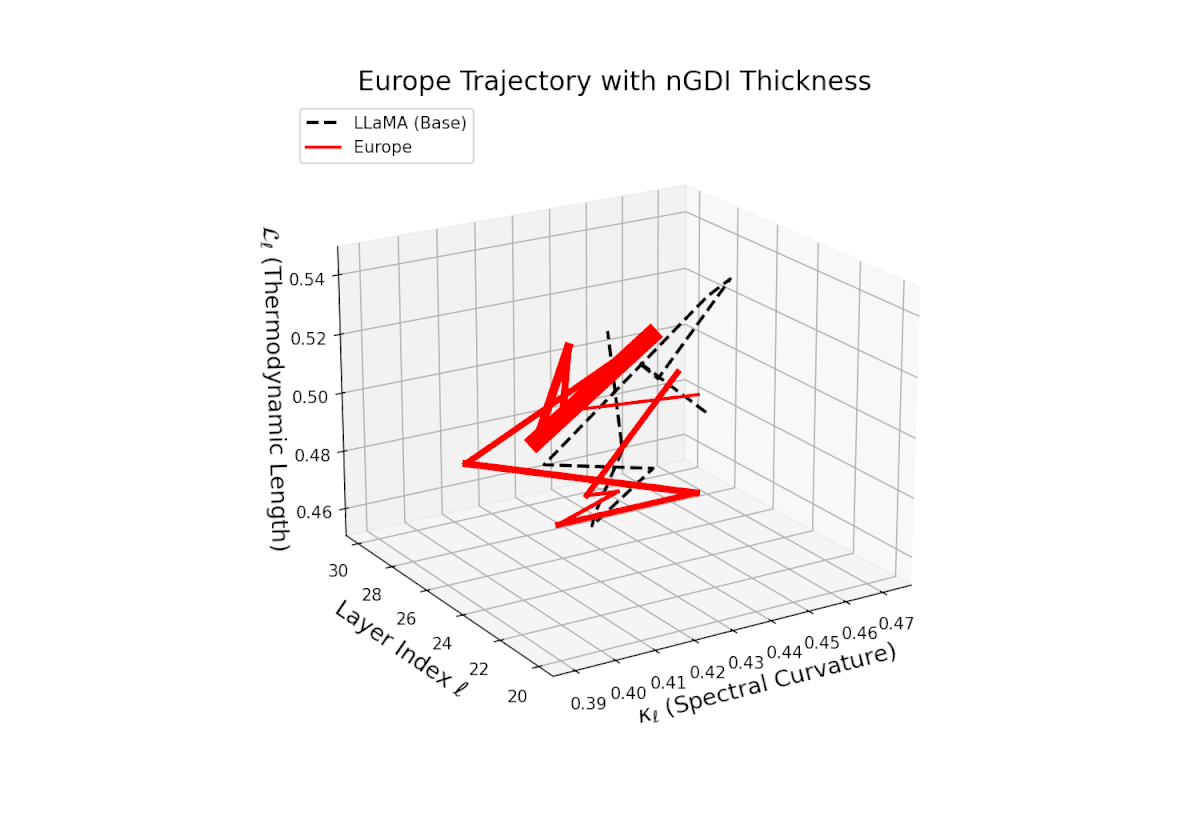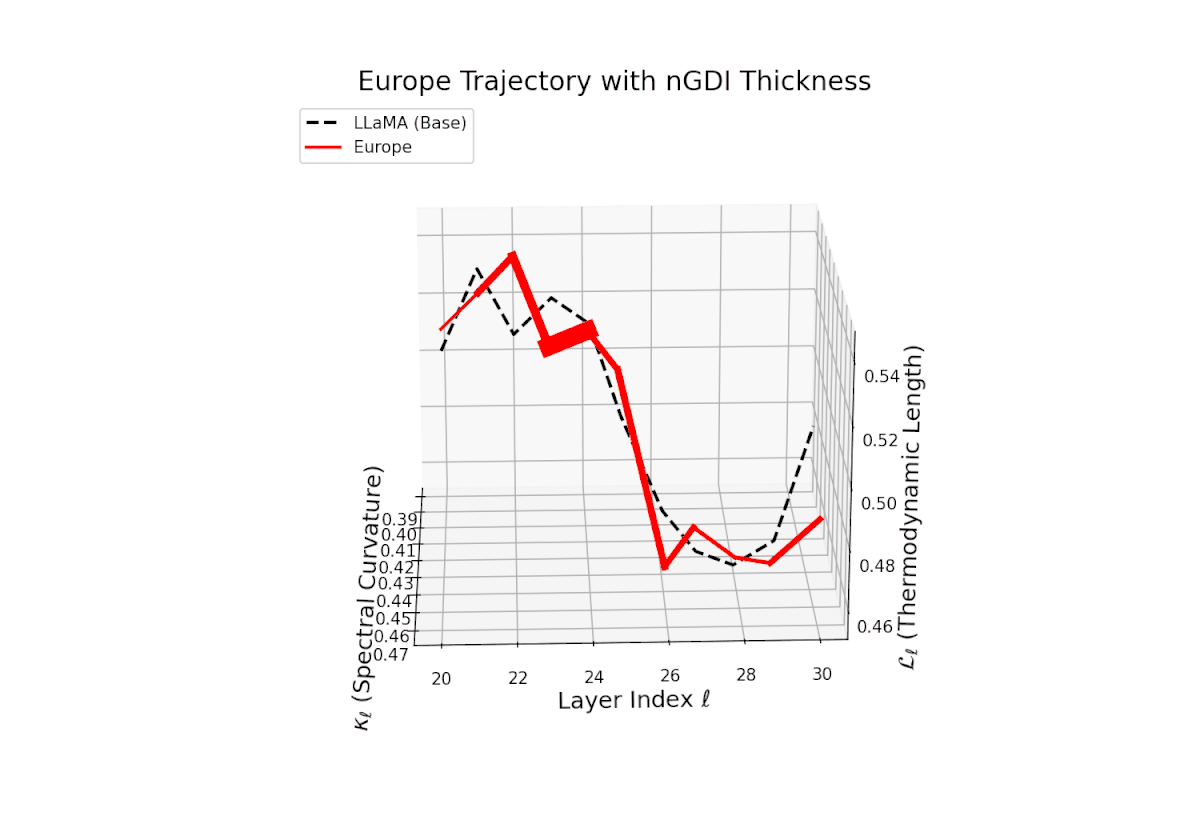
The Neural Genetic Dissimilarity Index dℓnGDI for Europe ranges from about 0.05 to 0.35, lower than Africa and Asia. The narrower thickness indicates modest latent divergence from the base model, suggesting shared semantic priors or closer alignment to base cultural contexts.
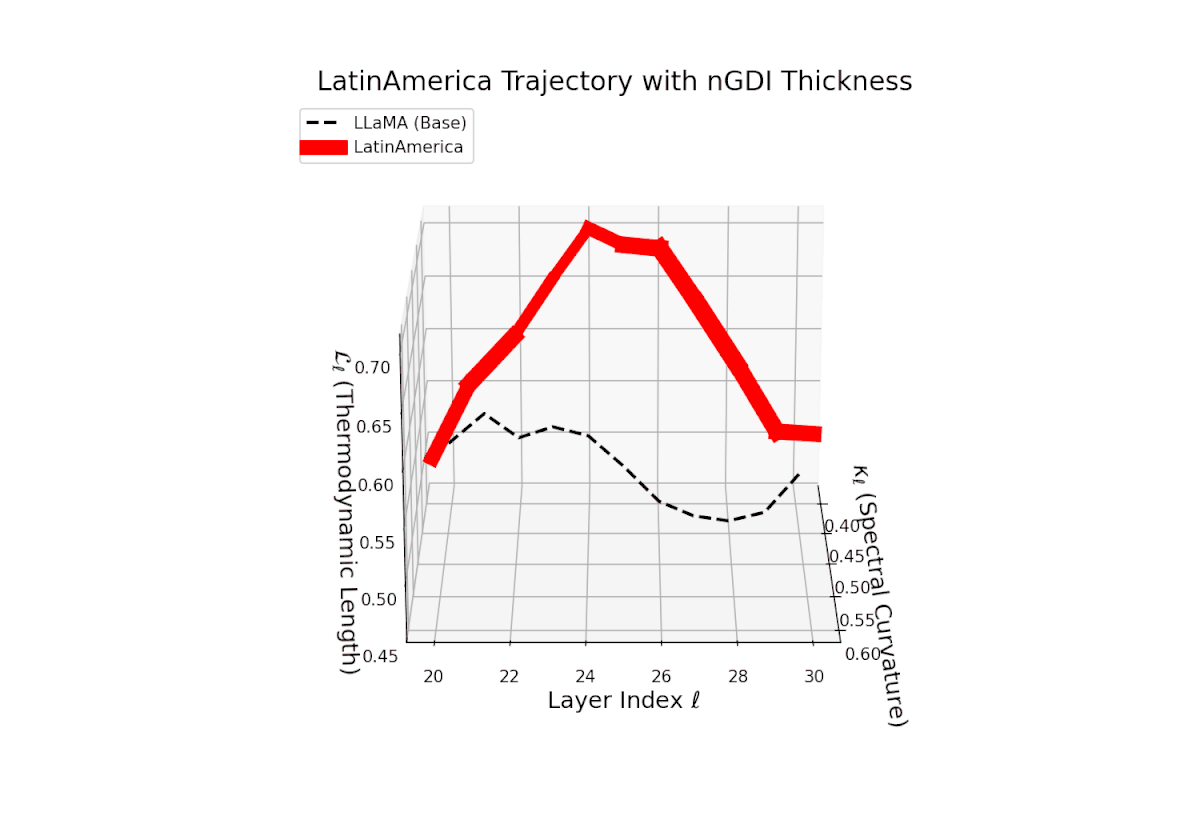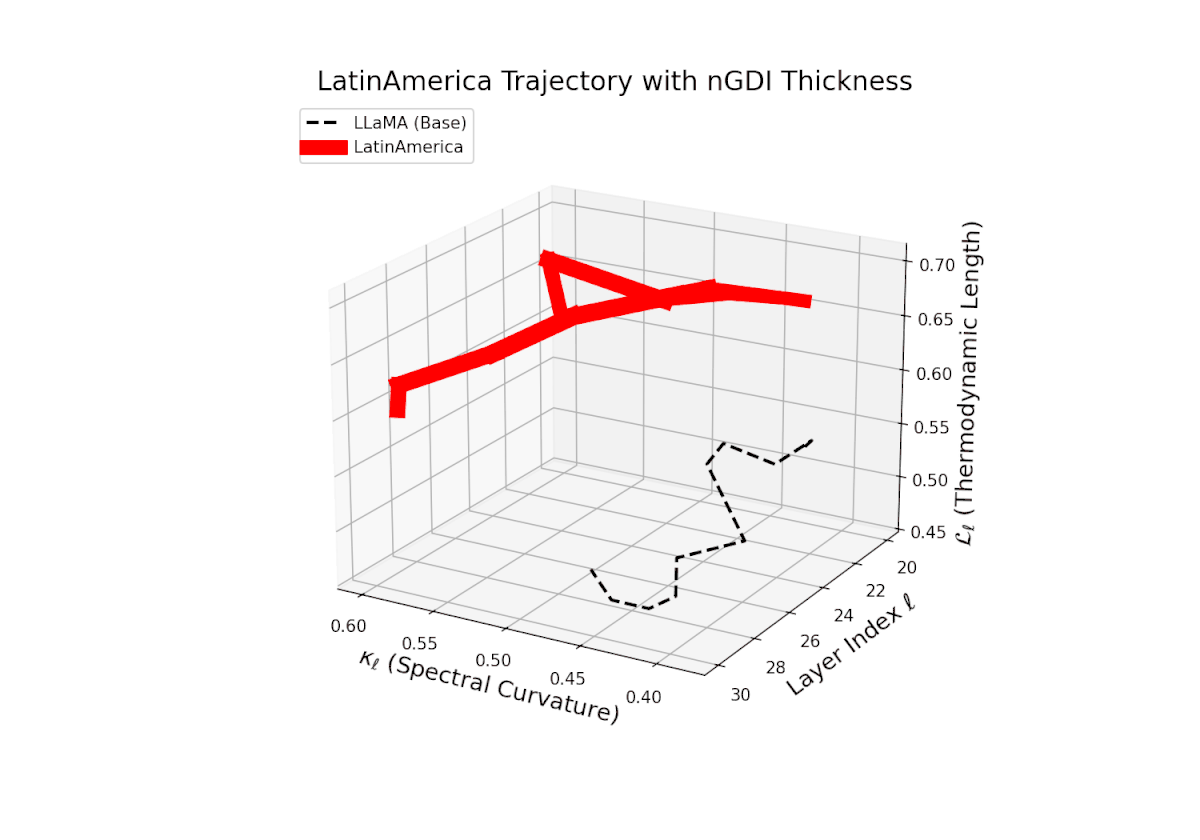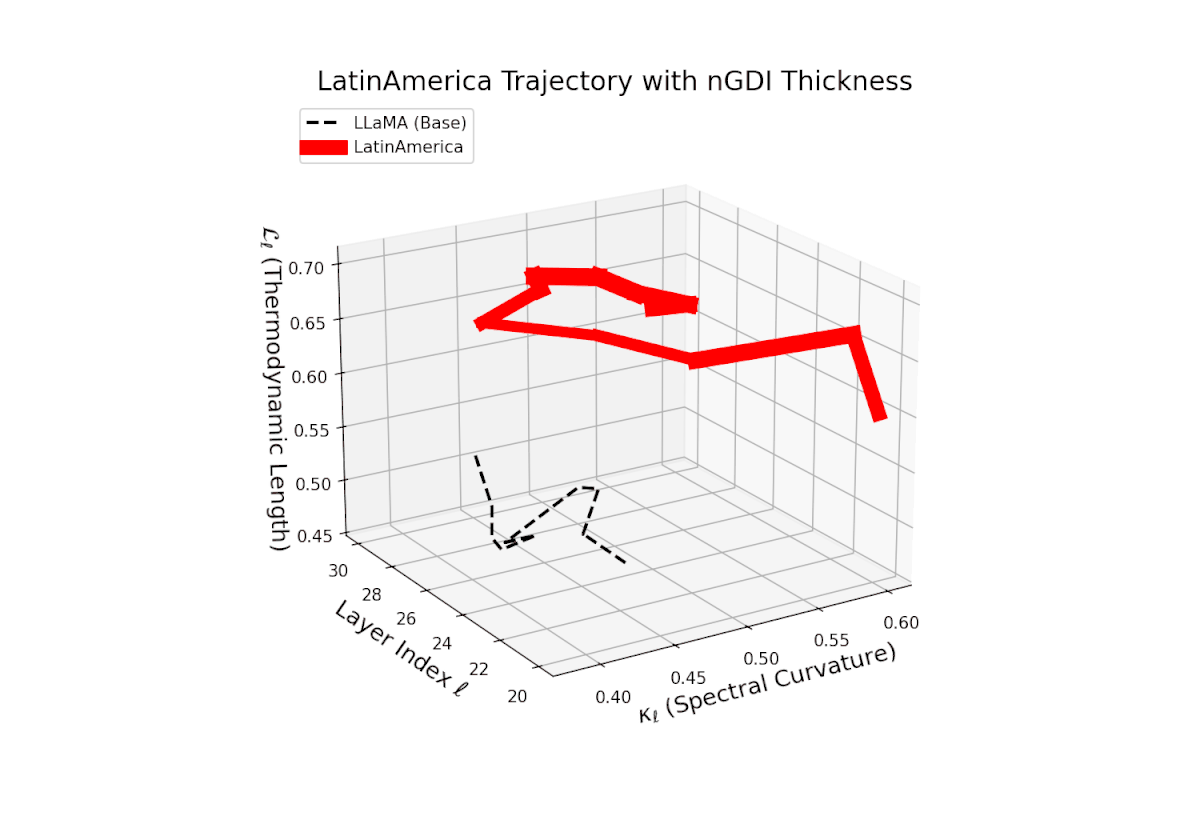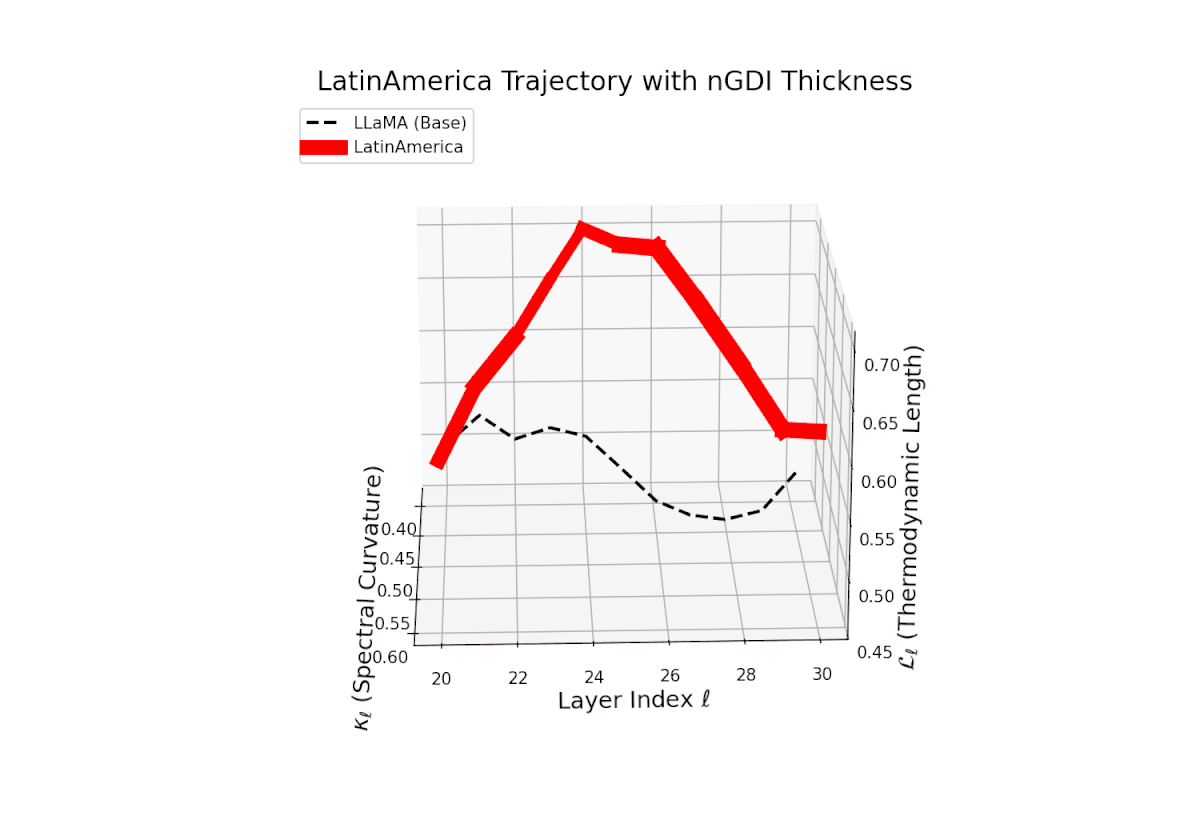
The Neural Genetic Dissimilarity Index dℓnGDI spans from 0.1 to 0.45 with moderate layerwise variability. The thickness highlights increased divergence in intermediate layers (ℓ ≈ 24 to 28), suggesting representational reshaping at these depths due to fine-tuning.
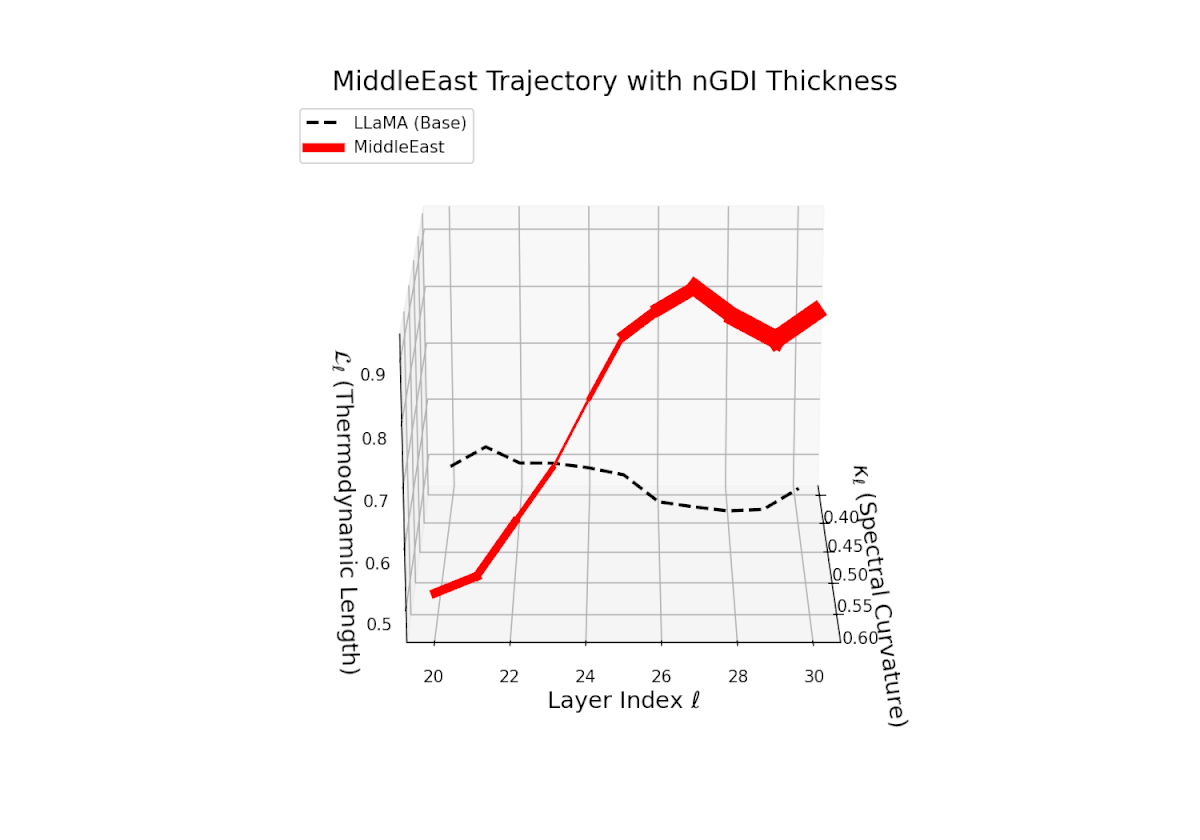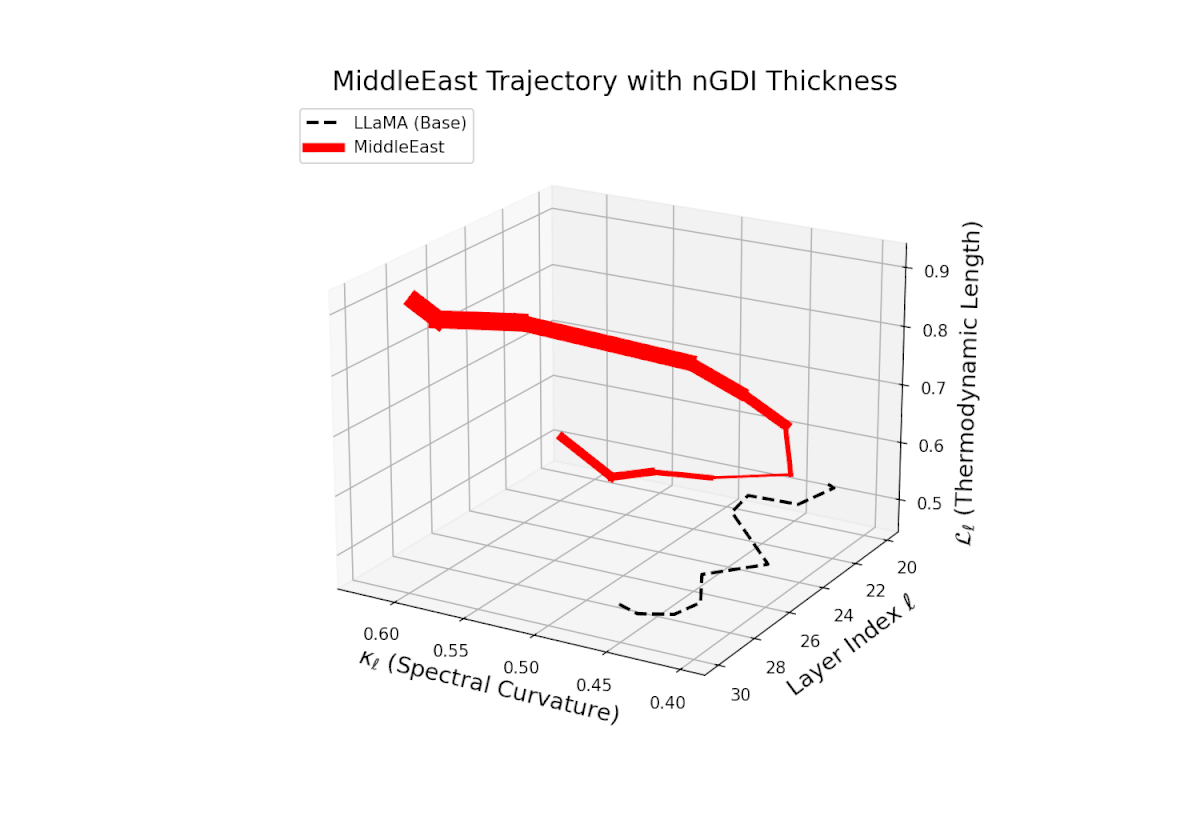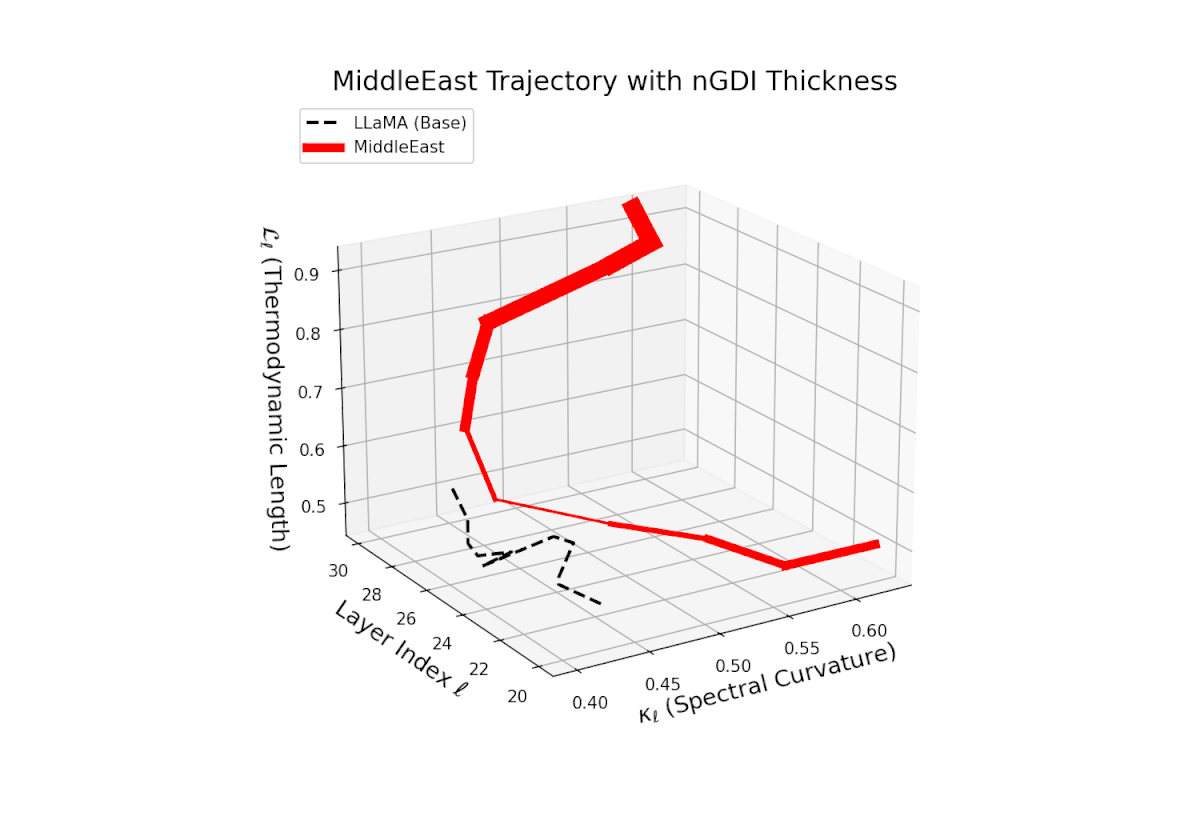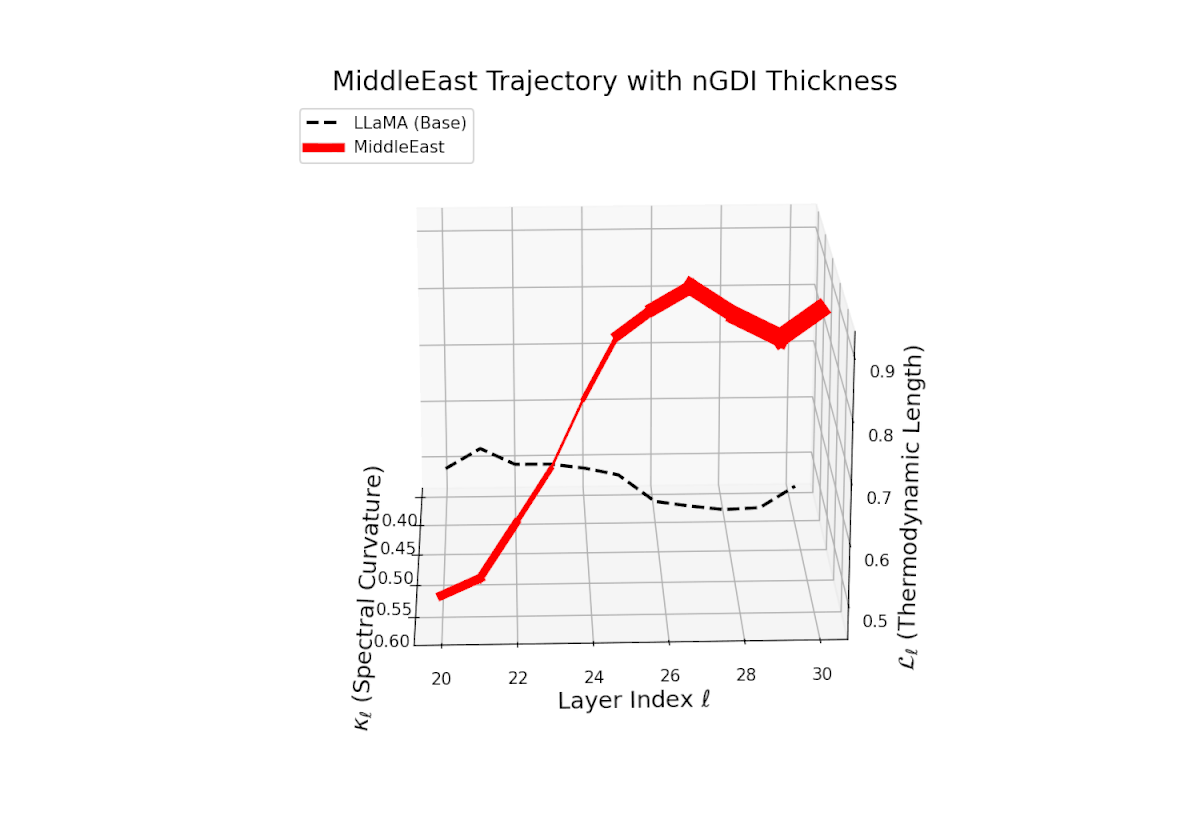
The Neural Genetic Dissimilarity Index dℓnGDI for Middle East ranges widely from 0.1 to 0.6, with a prominent peak near ℓ = 26. The pronounced thickness indicates substantial latent dissimilarity, reflecting distinct neural adaptation to cultural and linguistic specificity.
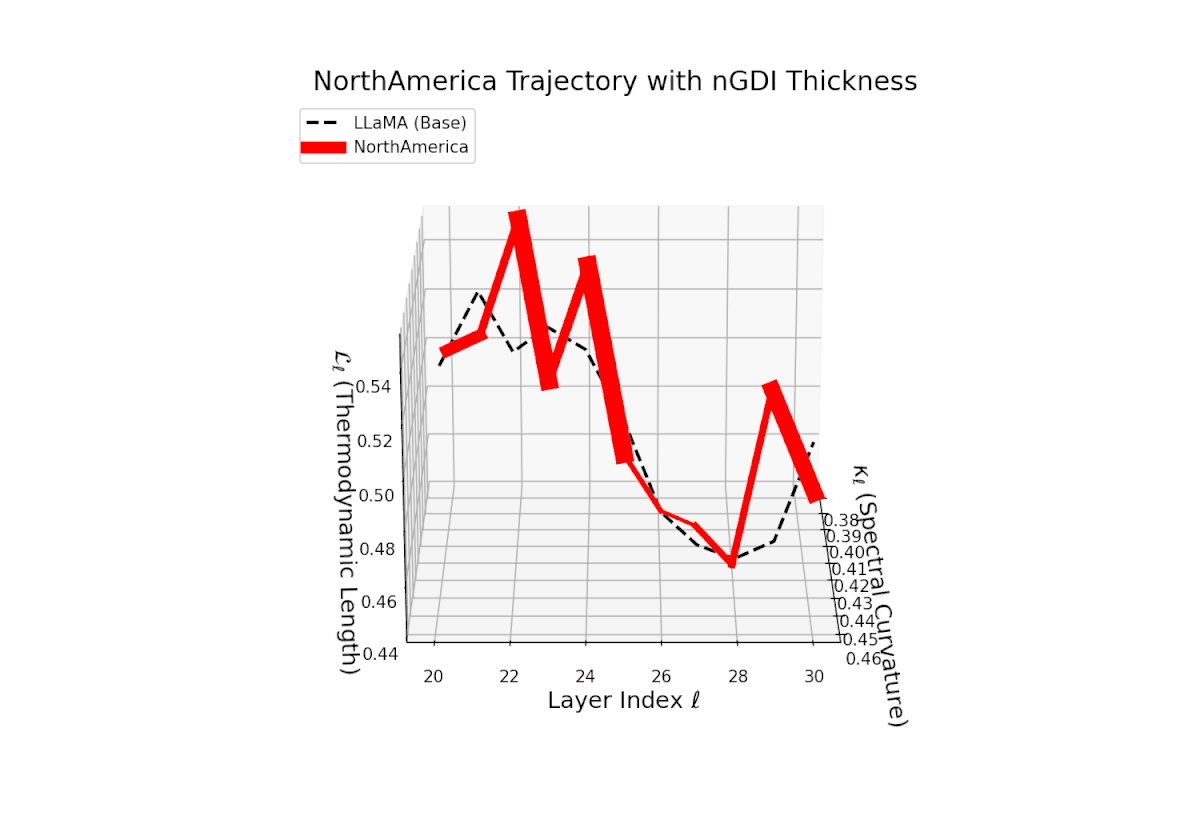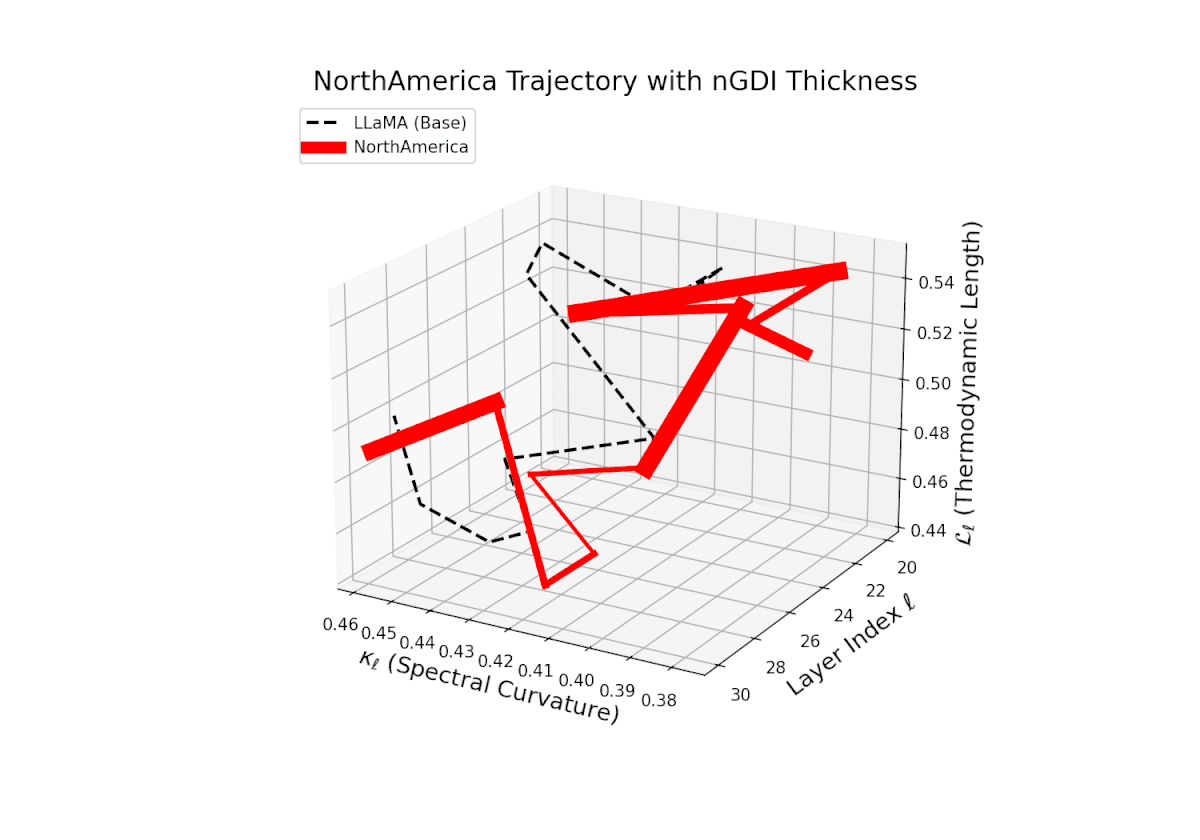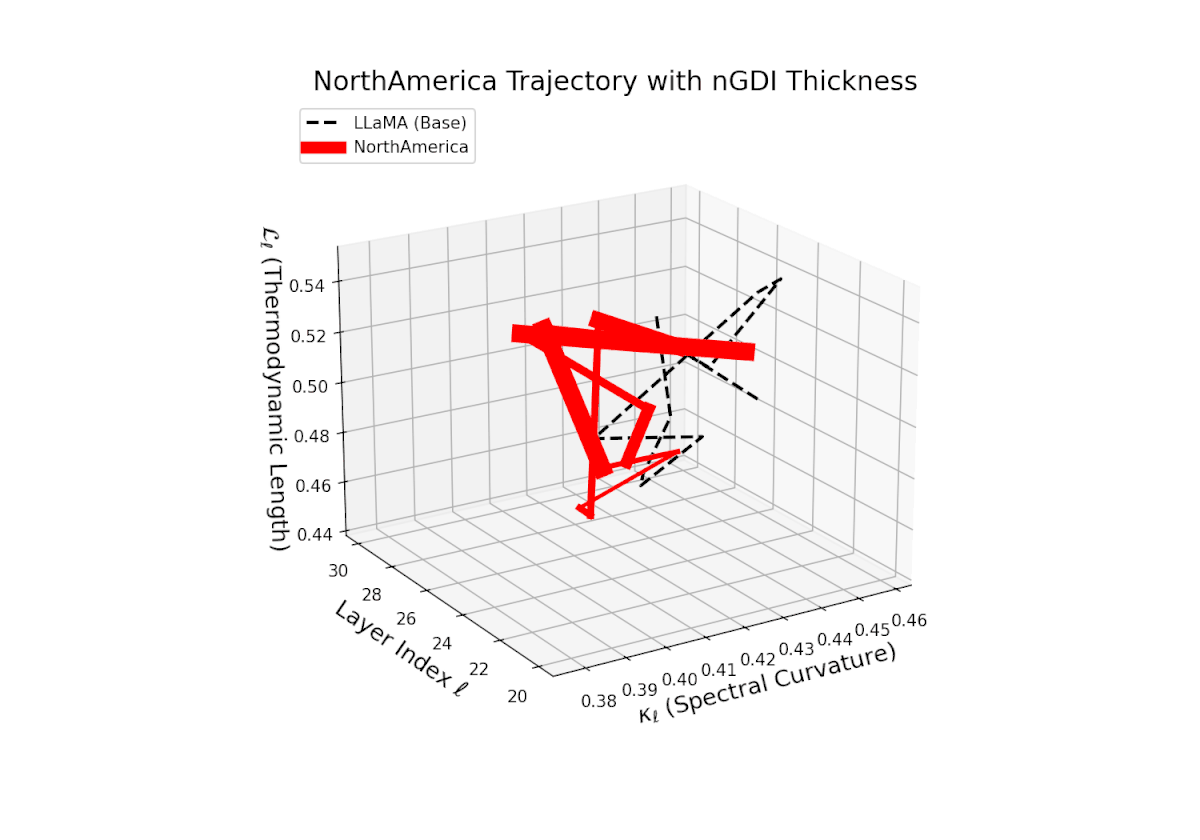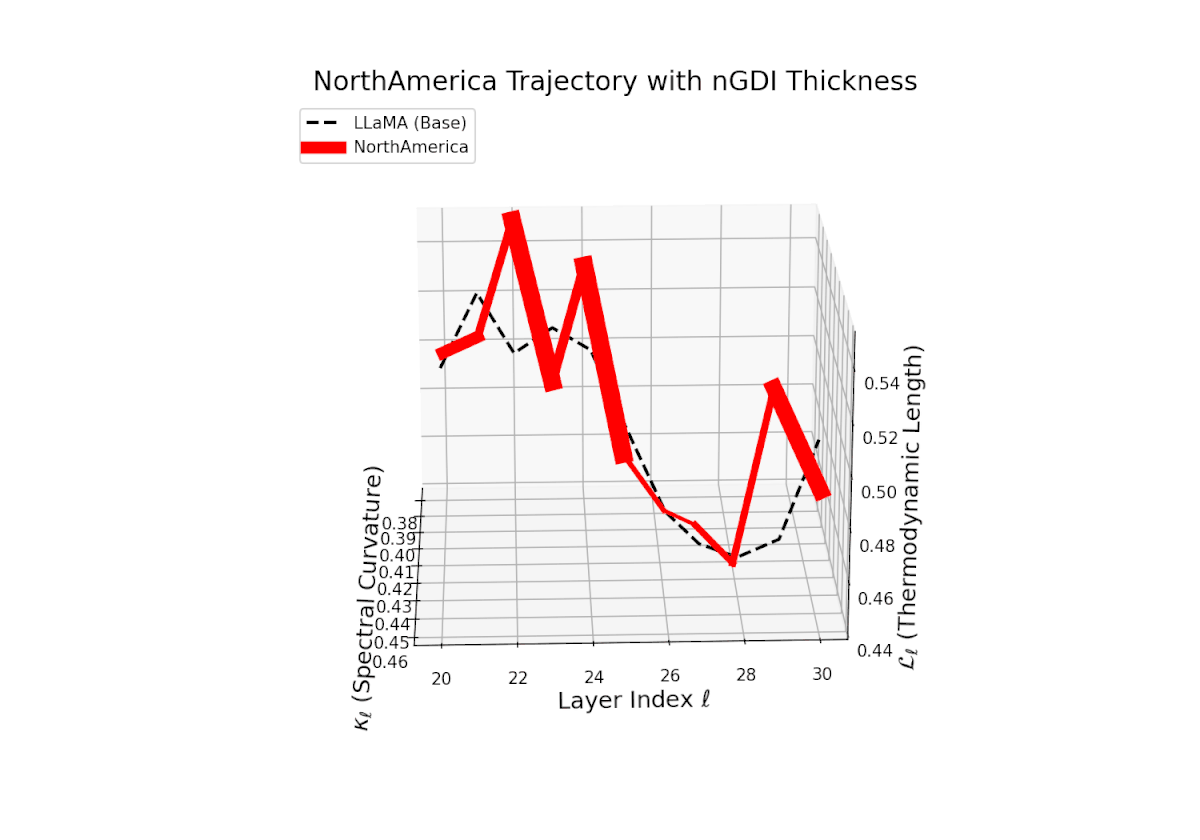
The Neural Genetic Dissimilarity Index dℓnGDI for North America shows the lowest overall values, roughly 0.05 to 0.3, indicating minimal latent genetic drift from the base. The subtle thickness variation suggests stable semantic representations across layers.
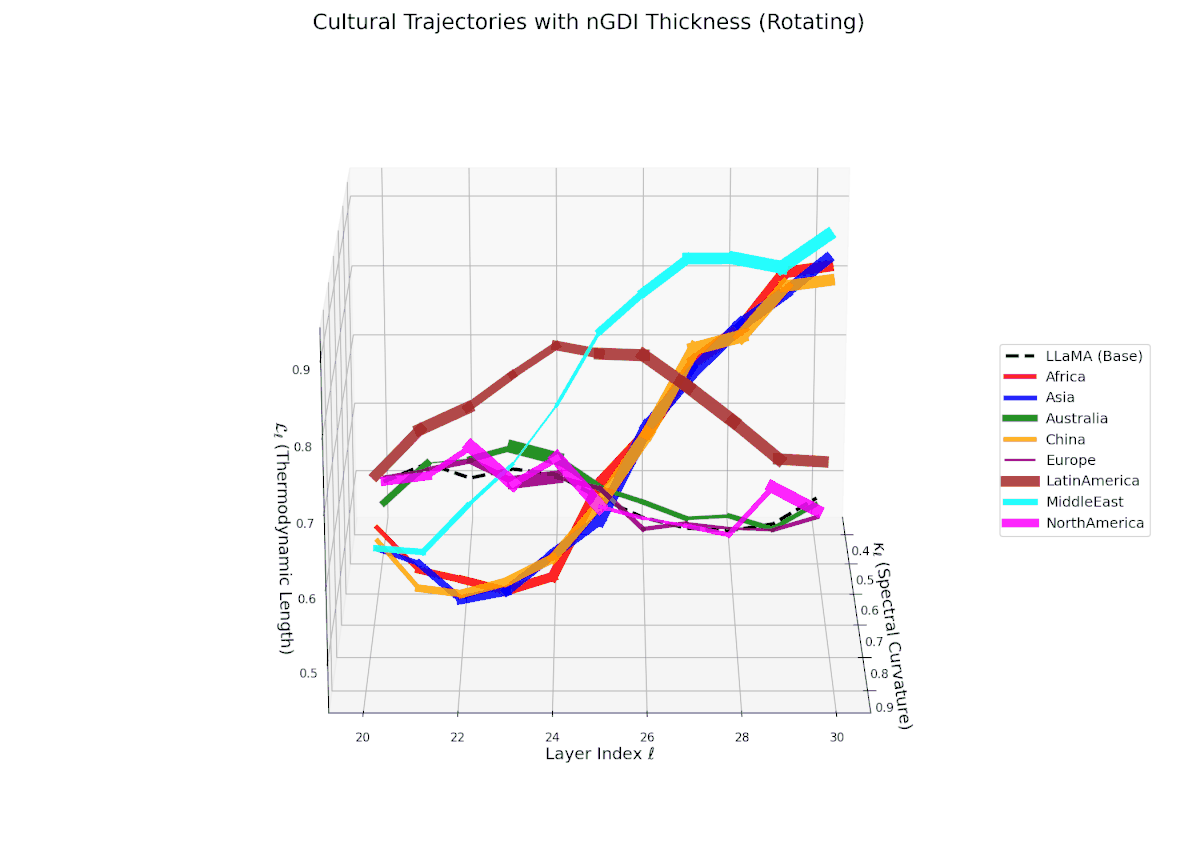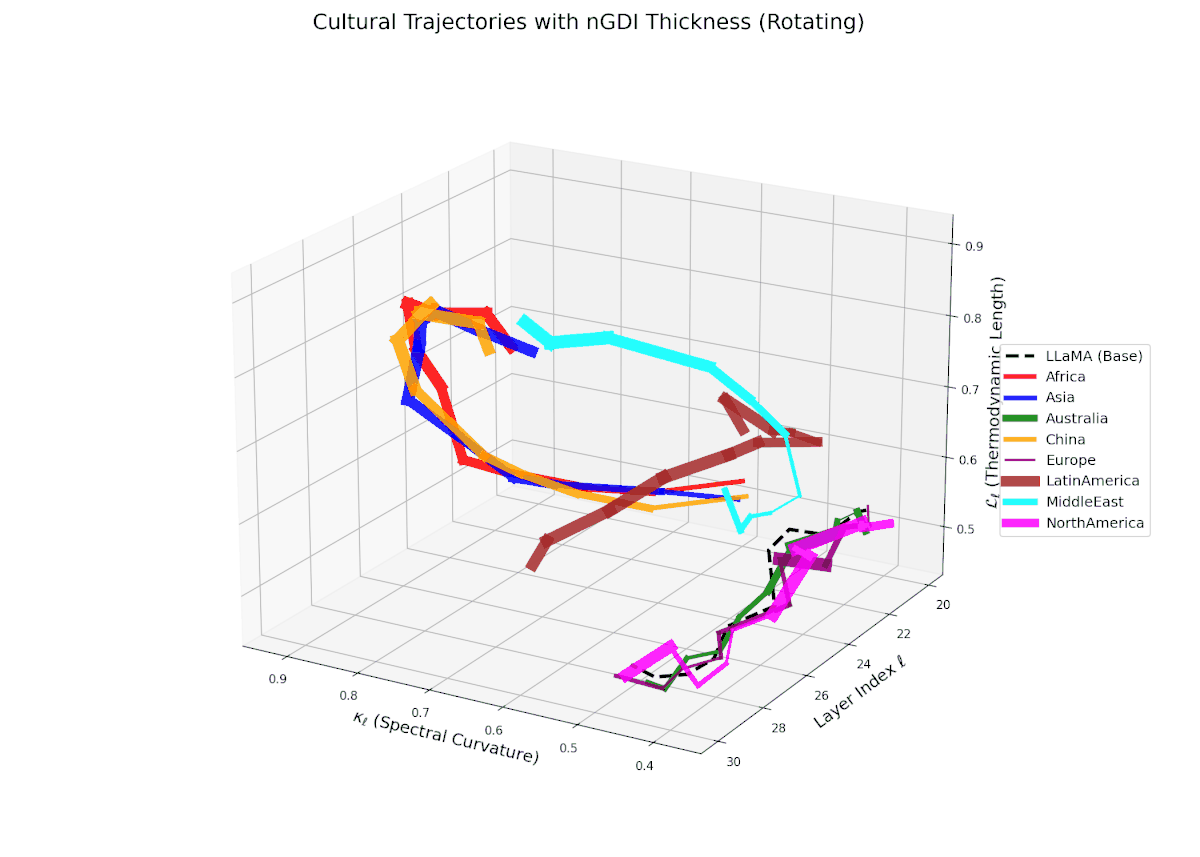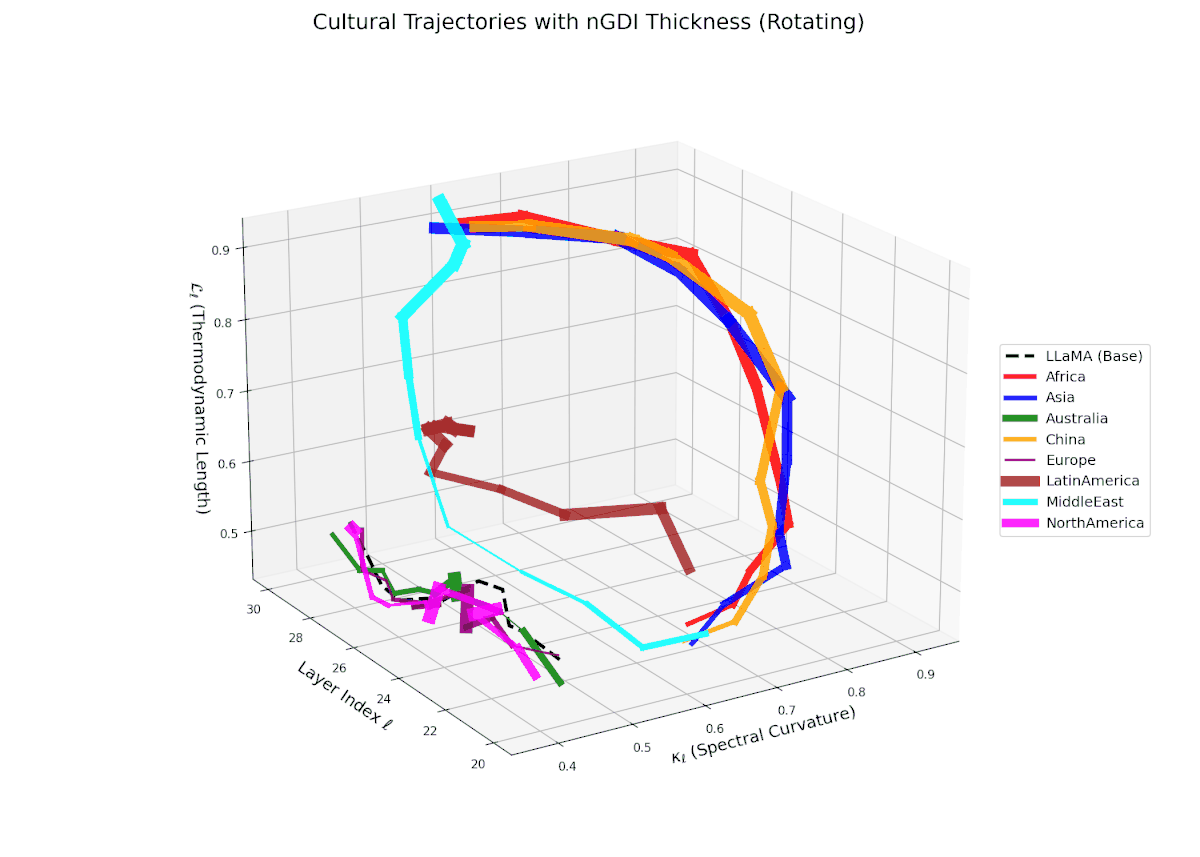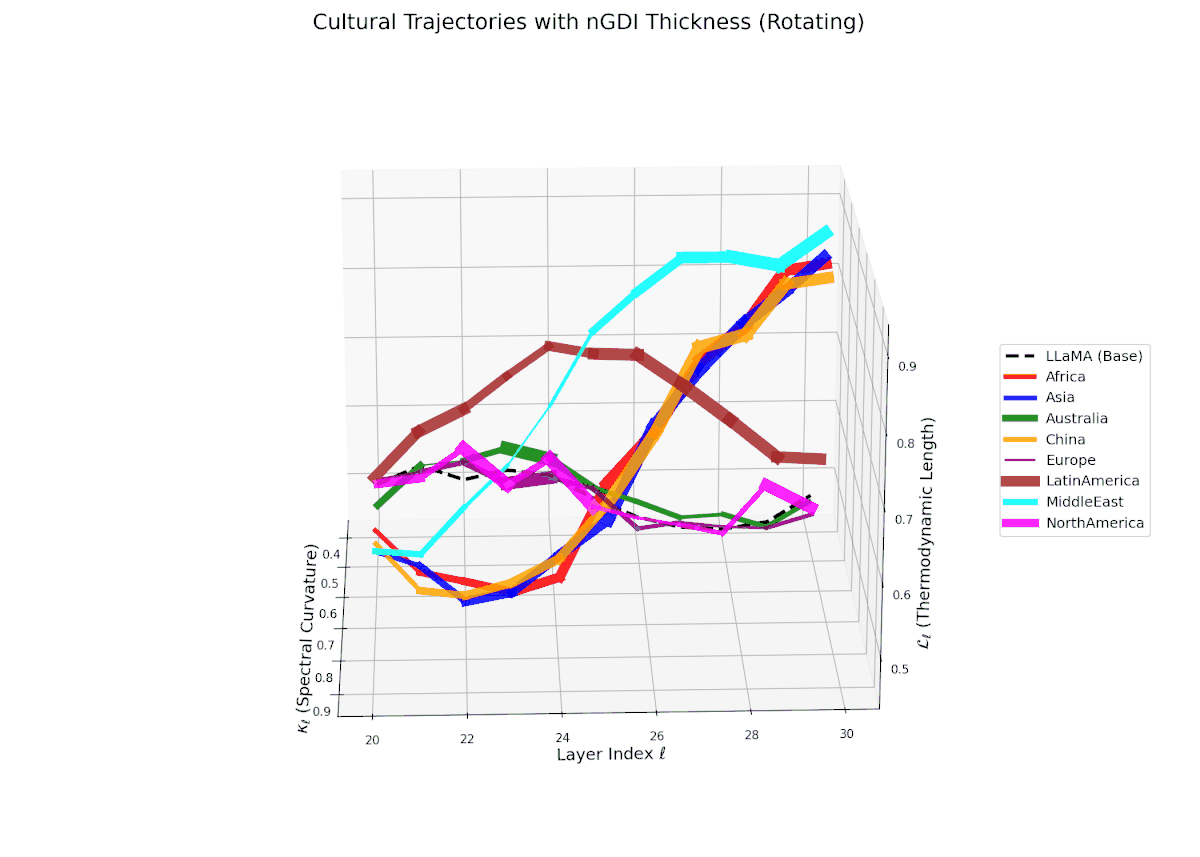
3D Neural Genetic Dissimilarity Index (dℓnGDI) Trajectories Comparing Fine-Tuned Models Against the LLaMA Base Model.
For each transformer layer ℓ ∈ {20, . . . , 30}, the metric dℓnGDI quantifies latent semantic genetic divergence relative to the base model.
The colored curves represent culturally fine-tuned model trajectories, while the black dashed curve denotes the LLaMA base reference.
Line thickness encodes the magnitude of dℓnGDI, highlighting layers with maximal representational shifts.
Mathematical Context:
The Neural Genetic Dissimilarity Index dℓnGDI is formally defined as a layerwise divergence metric in latent space measuring the geodesic or information-theoretic distance between the cultural fine-tuned model’s and base model’s manifold embeddings (312; 319).
This provides a rigorous geometric quantification of semantic drift across deep model layers.
Biological Analogy:
Analogous to genetic mutation hotspots in biological DNA recombination [6], the layerwise variation in dℓnGDI reveals critical neural depths where semantic realignment, adaptation, and cultural imprinting occur.
Models such as Africa and Middle East exhibit pronounced divergence, indicating region-specific evolutionary adaptations, while North America’s low divergence suggests semantic stability and close affinity to ancestral priors.
Mathematical Takeaway:
The offspring latent manifold at layer ℓ can be modeled as a nonlinear fusion of parental manifolds:
where α(ℓ) ∈ [0, 1] denotes the layer-dependent semantic dominance coefficient, dynamically modulating parental influence, and ε(ℓ) captures emergent nonlinear geometry beyond linear interpolation.
This formalism captures multi-layered integration, selective semantic imprinting, and complex evolutionary dynamics in transformer latent spaces, providing a principled framework for interpreting cultural neural DNA fusion and semantic innovation in multilingual AI systems.
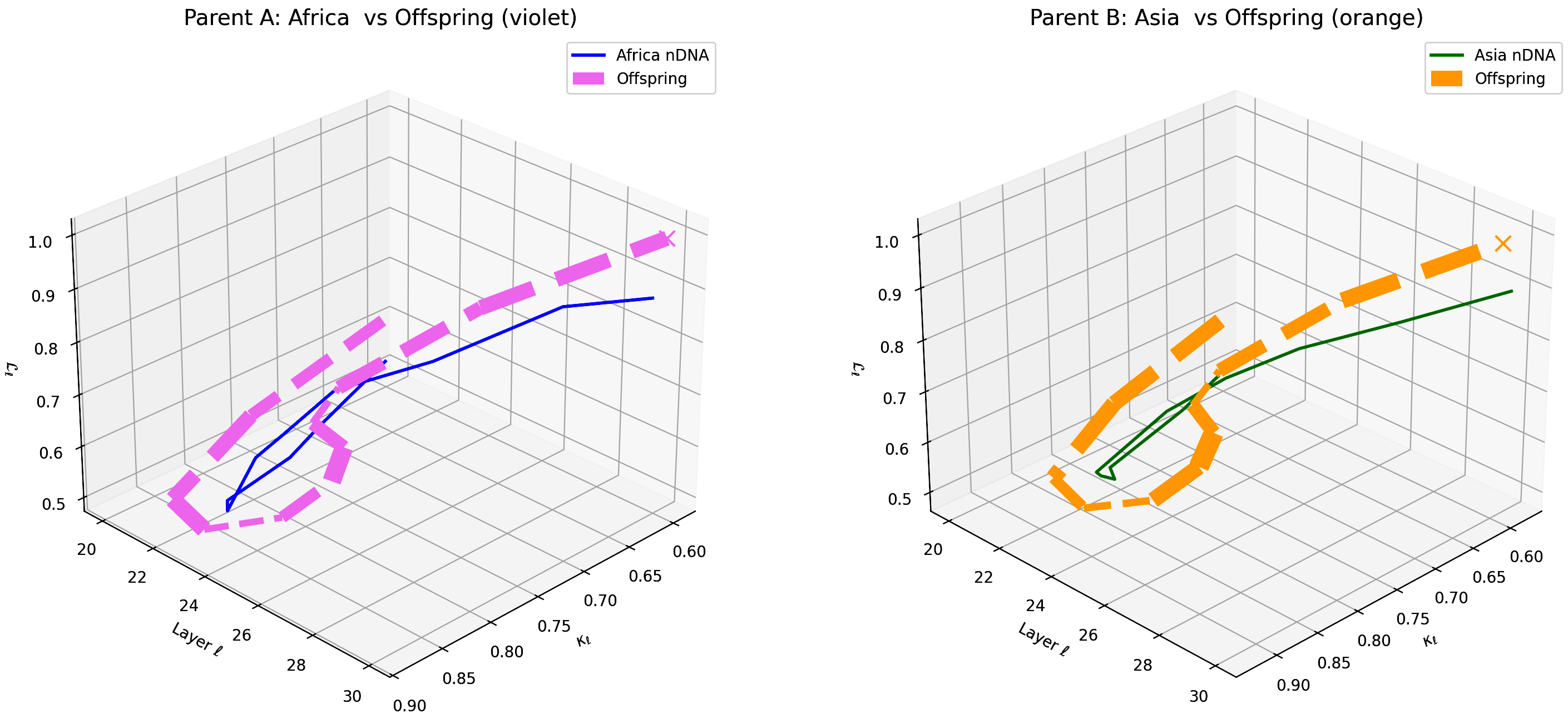
The plot compares the offspring model’s latent geometry (dashed lines) with Parent A (Africa, violet) and Parent B (Asia, orange) across transformer layers $\ell = 20$–$30$. Coordinates represent spectral curvature $\kappa_{\ell} \in [0.6, 0.9]$, torsion $\tau_{\ell} \in [0.5, 1.0]$, and latent radius $r_{\ell} \in [0.5, 1.0]$. The offspring aligns closer to Africa in early layers (20–24) and shifts toward Asia in deeper layers (26–30), revealing layer-specific trait dominance captured by $\mathrm{nTDS}_{\ell}$. Notably, the early layer alignment with Africa suggests retention of foundational lexical and syntactic features characteristic of African corpora, while deeper layer convergence toward Asia indicates higher-order semantic and cultural concept integration from Asian data. This gradient reflects progressive cultural imprinting across model depth, highlighting potential layers for targeted fine-tuning interventions to optimize cross-cultural knowledge blending.
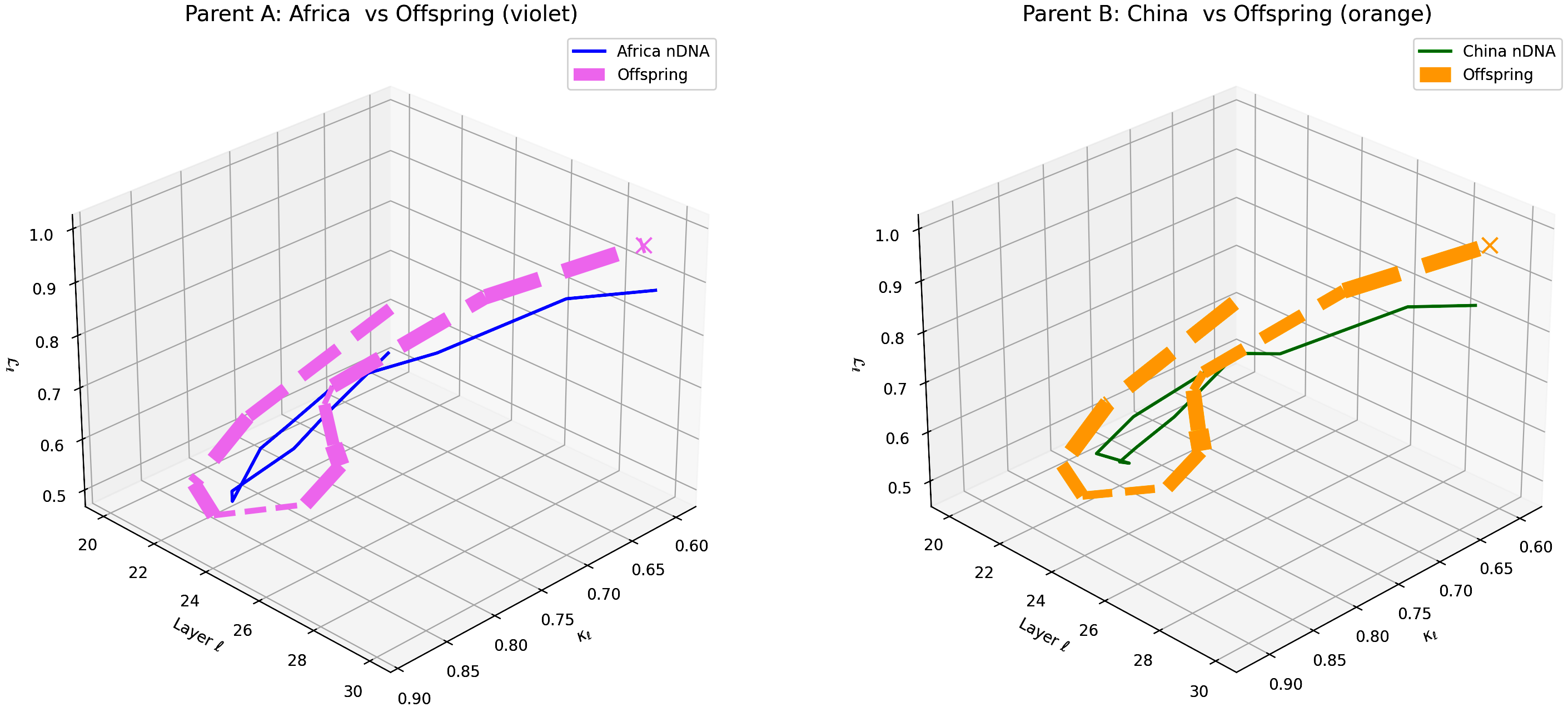
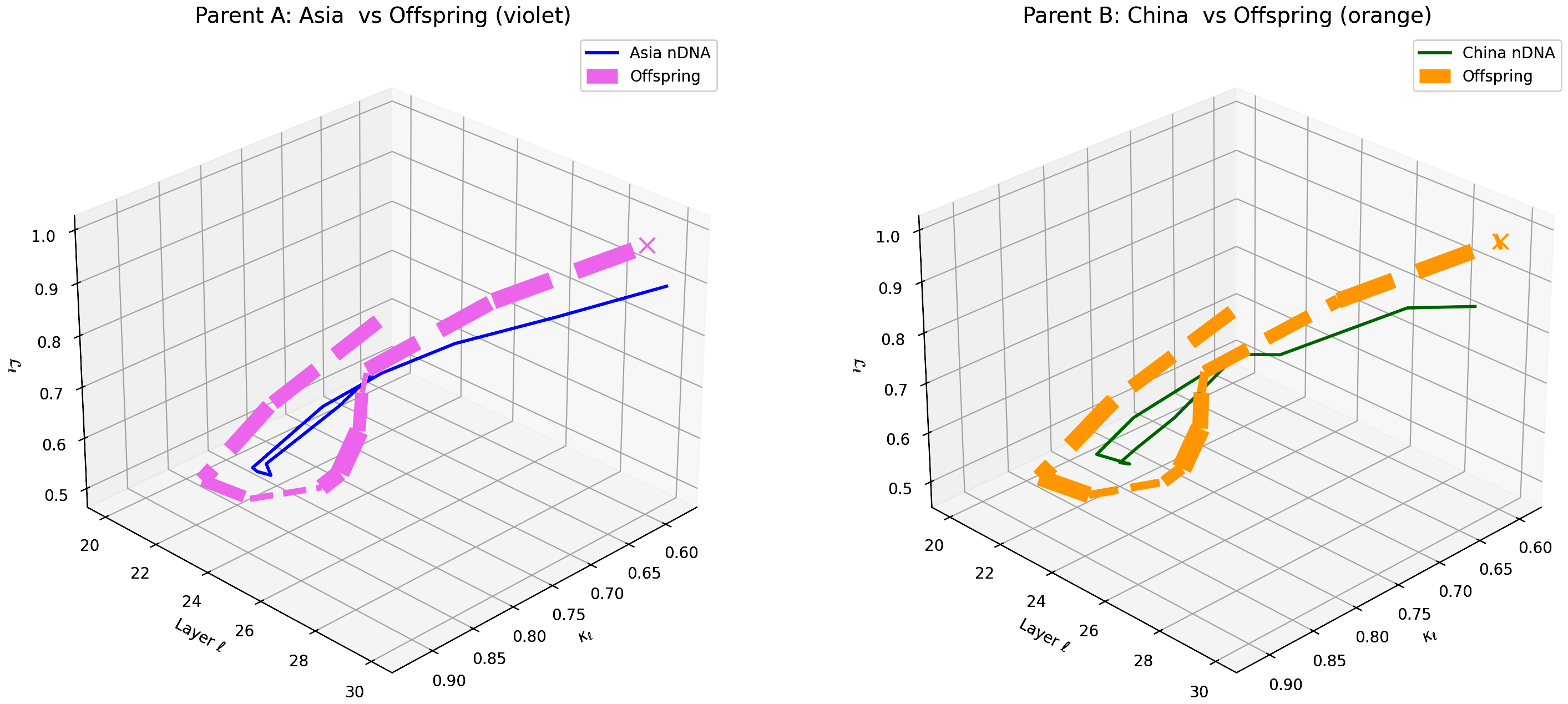
This plot depicts the offspring model’s latent geometry (dashed lines) compared against Parent A (Africa, violet) and Parent B (China, orange) across transformer layers $\ell = 20$–$30$. The coordinates correspond to spectral curvature $\kappa_{\ell} \in [0.6, 0.9]$, torsion $\tau_{\ell} \in [0.5, 1.0]$, and latent radius $r_{\ell} \in [0.5, 1.0]$. The offspring exhibits a pronounced alignment with Africa in early layers (20–24), while shifting more distinctly towards China in deeper layers (26–30). This layer-specific semantic inheritance reveals how foundational lexical and syntactic traits from African corpora are preserved early on, while abstract semantic and cultural patterns from Chinese data dominate the deeper, conceptual layers. Such a dynamic indicates nonlinear fusion effects where $\mathrm{nTDS}_{\ell}$ captures the nuanced dominance of distinct parental cultural priors across model depth. This detailed layerwise view offers actionable insights for targeted fine-tuning, facilitating enhanced cultural integration and semantic robustness in offspring models.
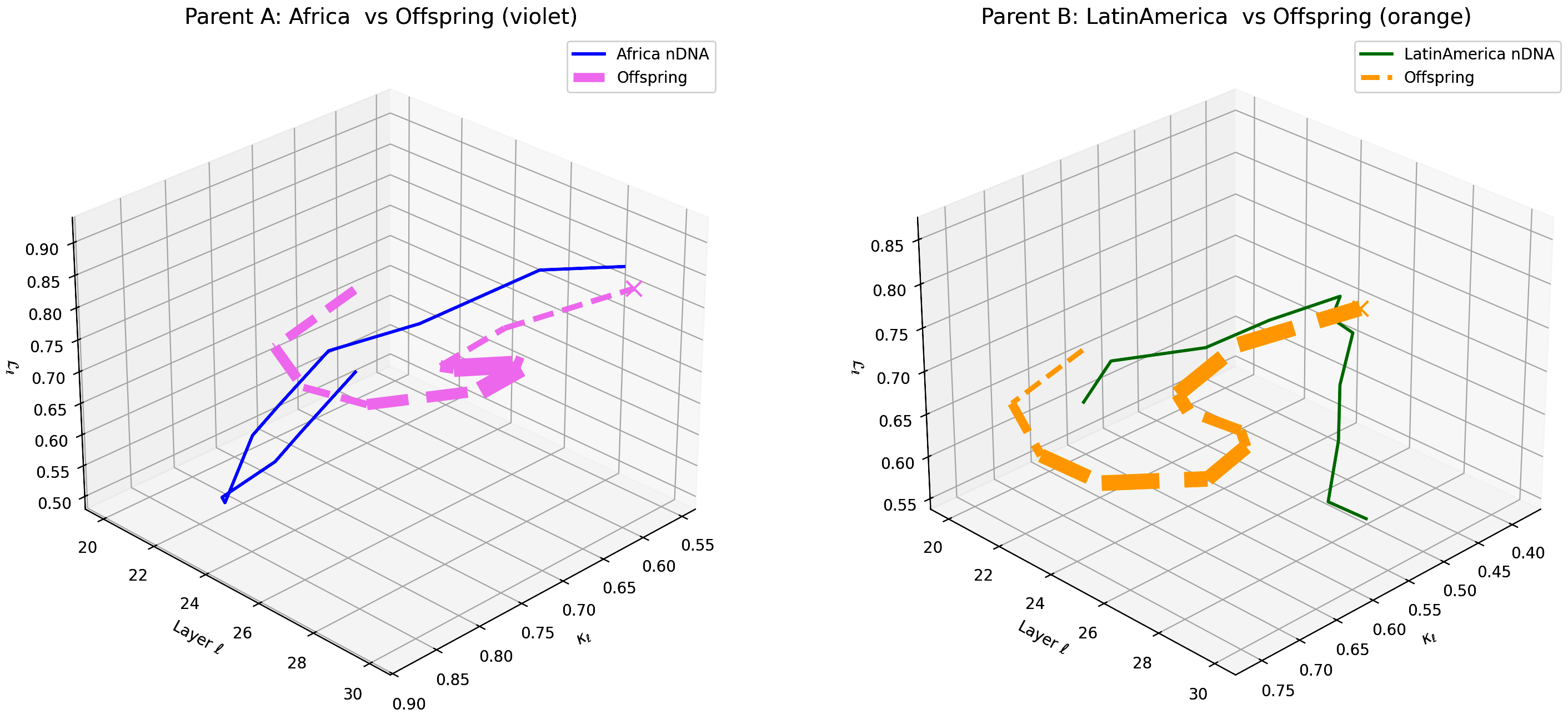
The figure contrasts the offspring model’s latent geometry (dashed lines) with Parent A (Africa, violet) and Parent B (Latin America, orange) across transformer layers $\ell = 20$–$30$. The plotted dimensions include spectral curvature $\kappa_{\ell} \in [0.4, 0.9]$, torsion $\tau_{\ell} \in [0.5, 0.9]$, and latent radius $r_{\ell} \in [0.5, 0.9]$. The offspring shows a dominant alignment with African traits in early layers (20–24), while gradually shifting toward Latin American influences in the deeper layers (26–30). This pattern reflects layerspecific semantic inheritance where foundational structural representations trace back to African corpora, with emergent abstract semantics shaped more by Latin American cultural embeddings. The nonlinear shift, effectively captured by $\mathrm{nTDS}_{\ell}$, illustrates complex cultural fusion beyond simplistic averaging. Such insights suggest targeted, depth-aware fine-tuning to reinforce semantic robustness and cultural adaptability in offspring foundation models.
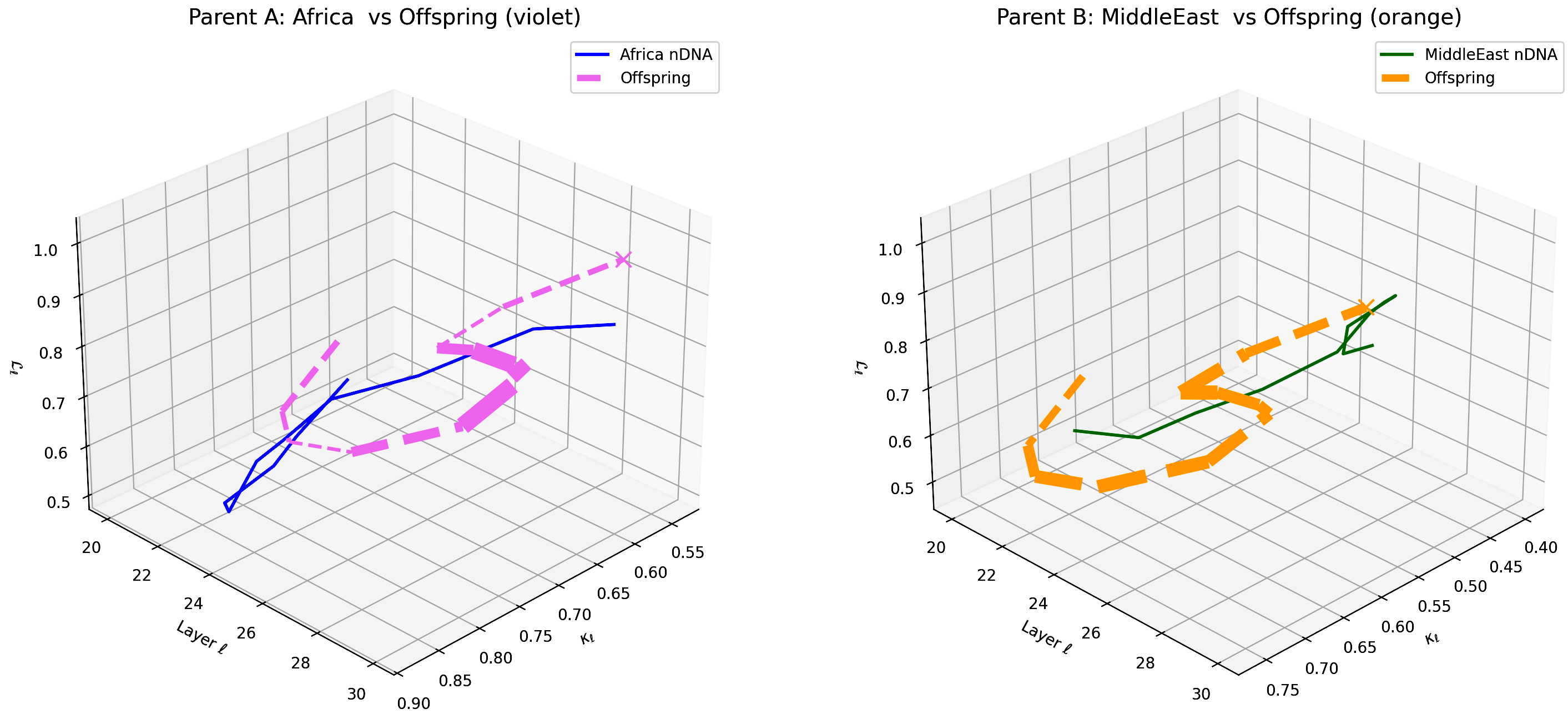
This plot illustrates the offspring model’s latent geometry (dashed lines) compared with Parent A (Africa, violet) and Parent B (Middle East, orange) across transformer layers $\ell = 20$–$30$. The axes depict spectral curvature $\kappa_{\ell} \in [0.4, 0.9]$, torsion $\tau_{\ell} \in [0.5, 1.0]$, and latent radius $r_{\ell} \in [0.5, 1.0]$. The offspring aligns more closely with African embeddings in early layers (20–25) but exhibits a notable shift toward Middle Eastern traits in deeper layers (26–30), reflecting a complex, nonlinear semantic inheritance captured by $\mathrm{nTDS}_{\ell}$. This layered trait dominance suggests that fundamental representational structures derive primarily from African data, while culturally nuanced semantics increasingly reflect Middle Eastern influences. These findings emphasize the importance of layer-specific interventions to optimize cultural expressivity and semantic fidelity in multilingual foundation models.
This visualization compares the offspring model’s latent geometry (dashed lines) with Parent A (Asia, violet) and Parent B (China, orange) over transformer layers $\ell = 20$–$30$. The plot axes denote spectral curvature $\kappa_{\ell} \in [0.6, 0.92]$, torsion $\tau_{\ell} \in [0.5, 1.0]$, and latent radius $r_{\ell} \in [0.48, 1.0]$. The offspring shows dominance of Asia traits at early layers (20–24) with a subtle transition toward Chinese traits at deeper layers (25–30), revealing a nuanced blend of regional semantic characteristics. This pattern highlights the layer-specific semantic inheritance and nonlinear fusion dynamics of the cultural priors, as captured by the $\mathrm{nTDS}_{\ell}$ metric. These findings suggest that foundational semantic structures are preserved from broader Asian corpora while fine-grained, culturally specific traits from Chinese data modulate deeper representational layers. Targeted layerwise interventions can leverage this insight to optimize semantic robustness and cultural expressivity in multilingual models.
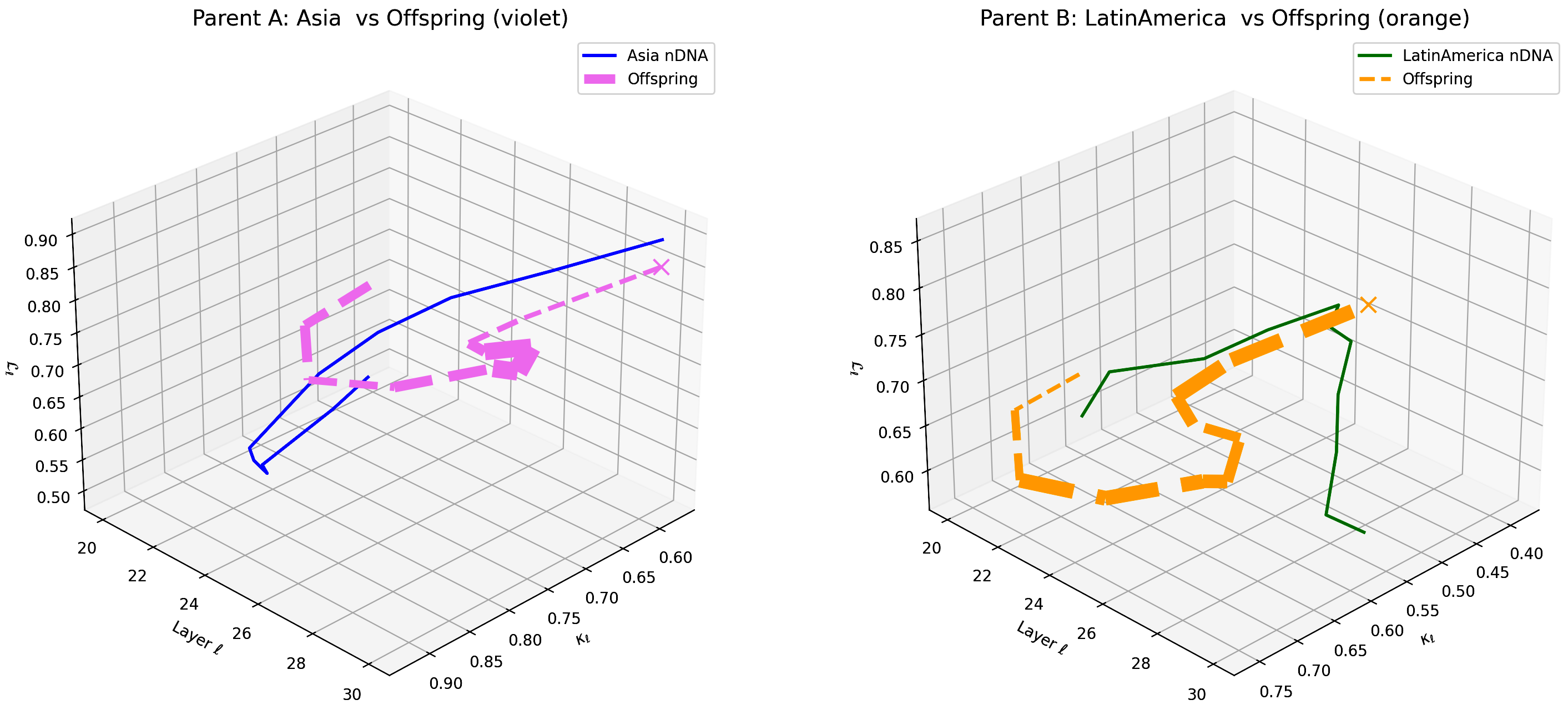
This plot contrasts the offspring model’s latent geometry (dashed lines) against Parent A (Asia, violet) and Parent B (Latin America, orange) over transformer layers $\ell = 20$–$30$. The coordinates denote spectral curvature $\kappa_{\ell} \in [0.48, 0.92]$, torsion $\tau_{\ell} \in [0.5, 0.9]$, and latent radius $r_{\ell} \in [0.48, 0.88]$. The offspring exhibits early alignment with Asian semantic traits (20–25) before shifting towards Latin American characteristics in deeper layers (26–30), showcasing a distinct layer-dependent cultural trait fusion. This pattern highlights complex, nonlinear semantic inheritance, reflecting how broad linguistic features are preserved while culturally specific nuances emerge later. Such insights enable precise layerwise tuning strategies to enhance multicultural semantic coherence and adaptivity in large language models.
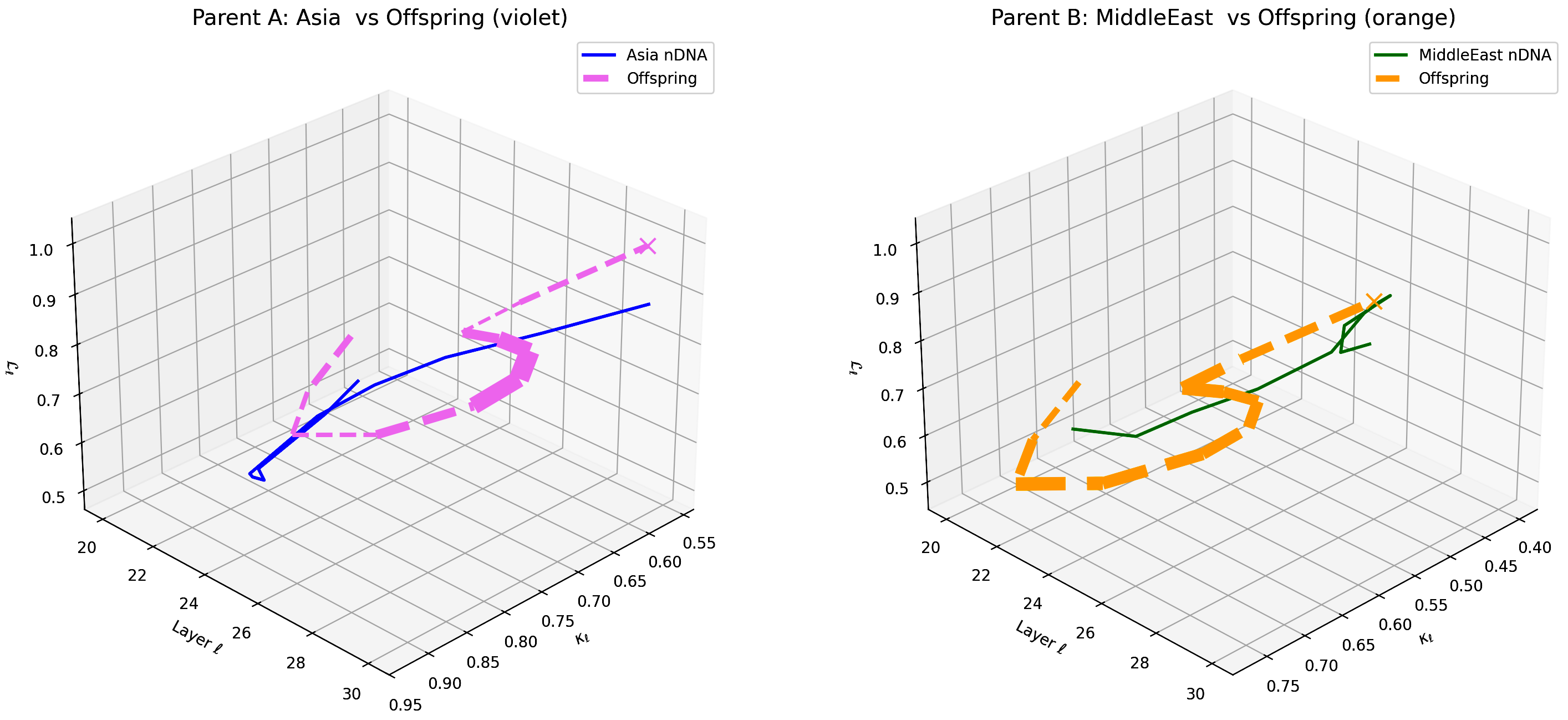
This visualization compares the offspring model’s latent geometry (dashed lines) with Parent A (Asia, violet) and Parent B (Middle East, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell} \in [0.55, 0.95]$, torsion $\tau_{\ell} \in [0.48, 1.05]$, and latent radius $r_{\ell} \in [0.45, 1.05]$. The offspring shows strong resemblance to Asian semantic structures in early layers (20–24), followed by a shift towards Middle Eastern traits in deeper layers (25–30), illustrating layer-specific semantic dominance. This pattern reveals a dynamic, nonlinear integration of cultural priors, emphasizing how foundational and abstract semantics are differentially inherited. Such granular insights provide actionable guidance for layer-targeted adaptation to optimize cross-cultural generalization.
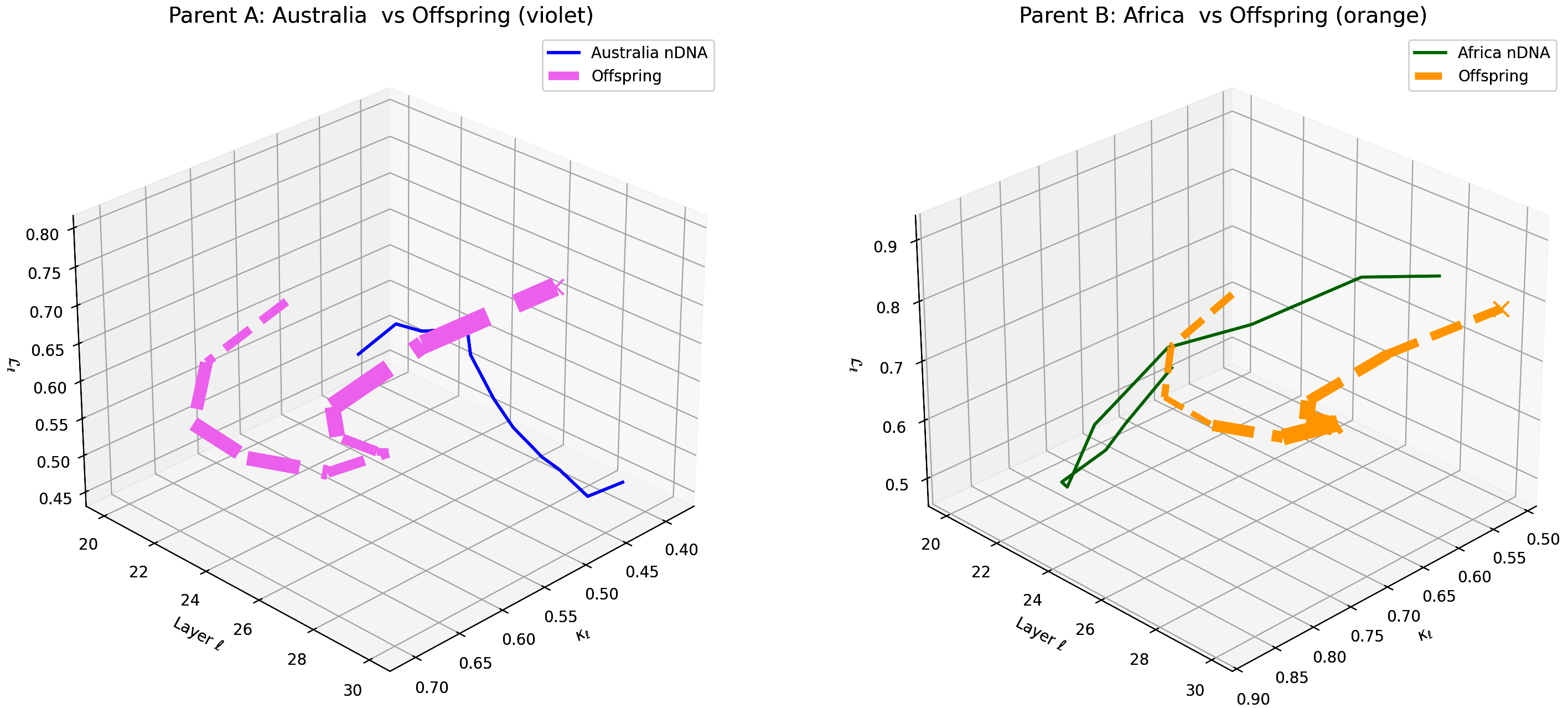
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Australia, violet) and Parent B (Africa, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a notable resemblance to Australian semantic features in early layers (20–24) and gradually transitions towards African semantic characteristics in deeper layers (25–30), reflecting layer-dependent semantic inheritance and dominance. This pattern underscores the complex interplay and integration of cultural priors within the offspring’s latent geometry. These insights highlight opportunities for layer-wise model adaptation to improve semantic fidelity and cross-cultural generalization.
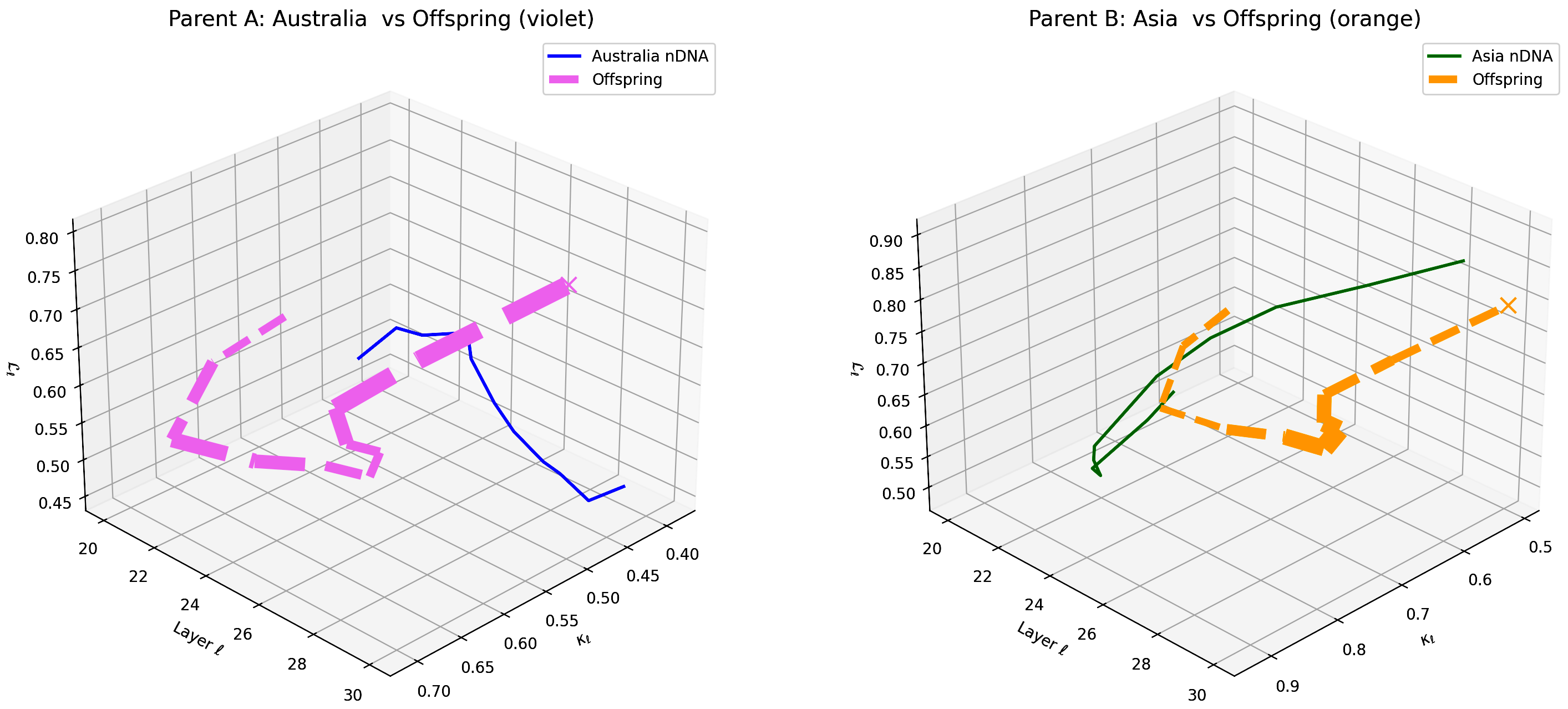
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Australia, violet) and Parent B (Asia, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory shows a strong resemblance to Australian semantic features in early layers (20–24) before gradually shifting toward Asian semantic characteristics in deeper layers (25–30), reflecting layer-dependent semantic inheritance and dominance. This pattern highlights the complex interplay and integration of cultural priors within the offspring’s latent geometry. These insights suggest promising directions for layer-wise model adaptation to enhance semantic fidelity and cross-cultural generalization.
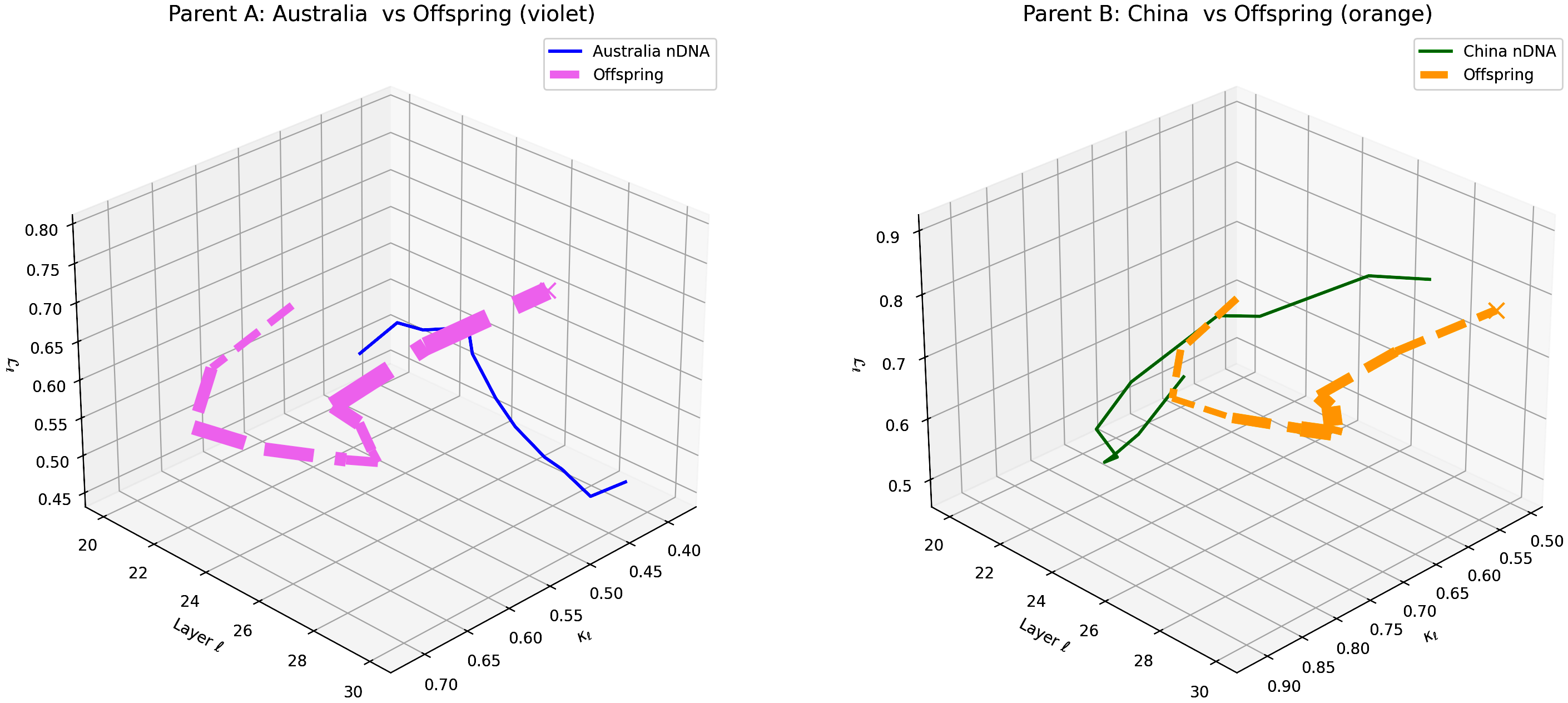
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Australia, violet) and Parent B (China, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory shows a clear resemblance to Australian semantic structures in early layers (20–24) and shifts towards Chinese semantic characteristics in deeper layers (25–30), illustrating layer-specific semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest layerwise adaptation opportunities to enhance semantic fidelity and cross-cultural generalization.
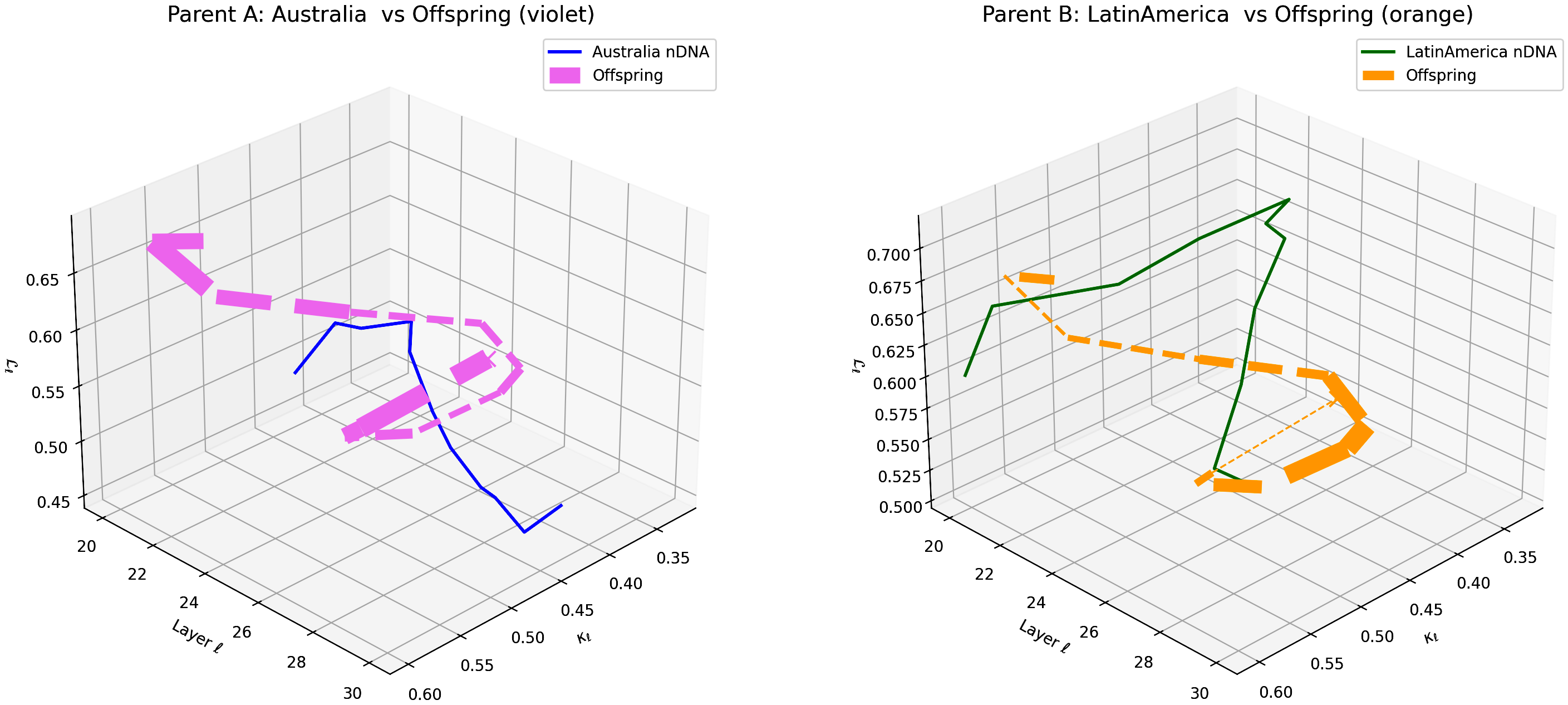
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Australia, violet) and Parent B (Latin America, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory demonstrates a strong similarity to Australian semantic patterns in early layers (20–24) and transitions toward Latin American semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This behavior highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest potential layer-wise adaptation strategies to enhance semantic fidelity and cross-cultural generalization.
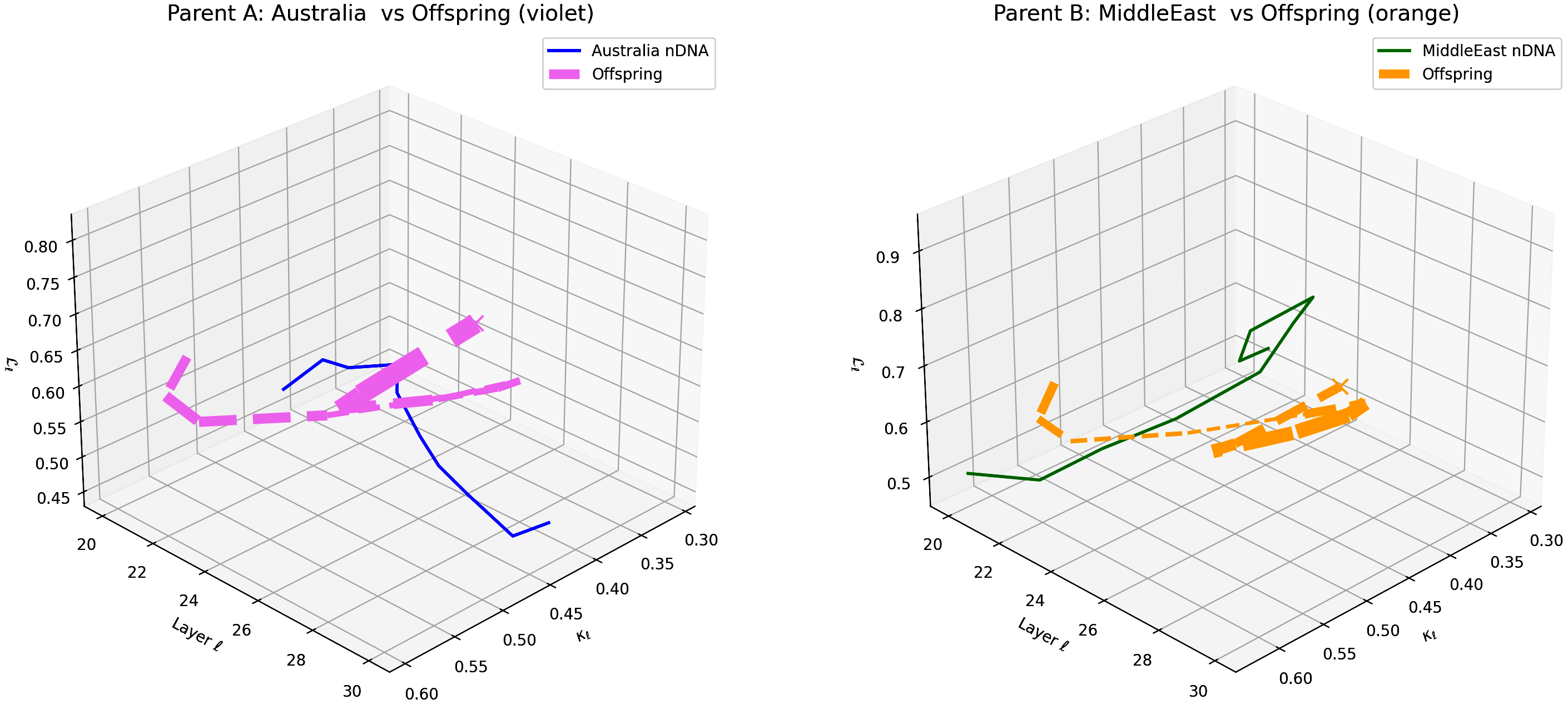
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Australia, violet) and Parent B (Middle East, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a pronounced resemblance to Australian semantic features in early layers (20–24) and shifts towards Middle Eastern semantic characteristics in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex interplay of cultural priors within the offspring’s latent geometry. These insights point to layer-wise adaptation strategies for enhancing semantic fidelity and cross-cultural generalization.
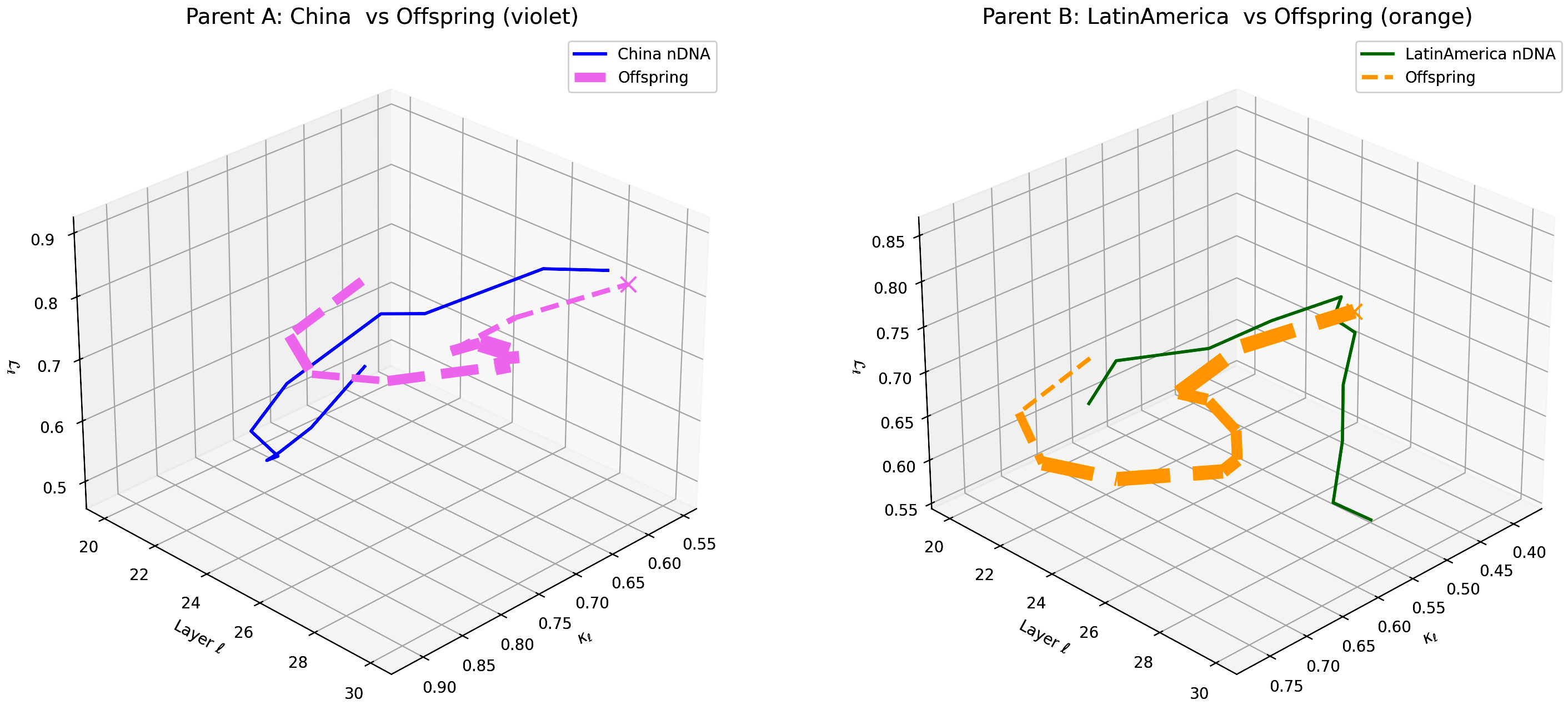
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (China, violet) and Parent B (Latin America, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory demonstrates a close resemblance to Chinese semantic patterns in early layers (20–24) with a gradual transition toward Latin American semantic traits in deeper layers (25–30), highlighting layer-dependent semantic inheritance and dominance. This pattern reveals the complex integration of cultural priors within the offspring’s latent geometry. These findings suggest layer-wise adaptation to enhance semantic fidelity and cross-cultural generalization.
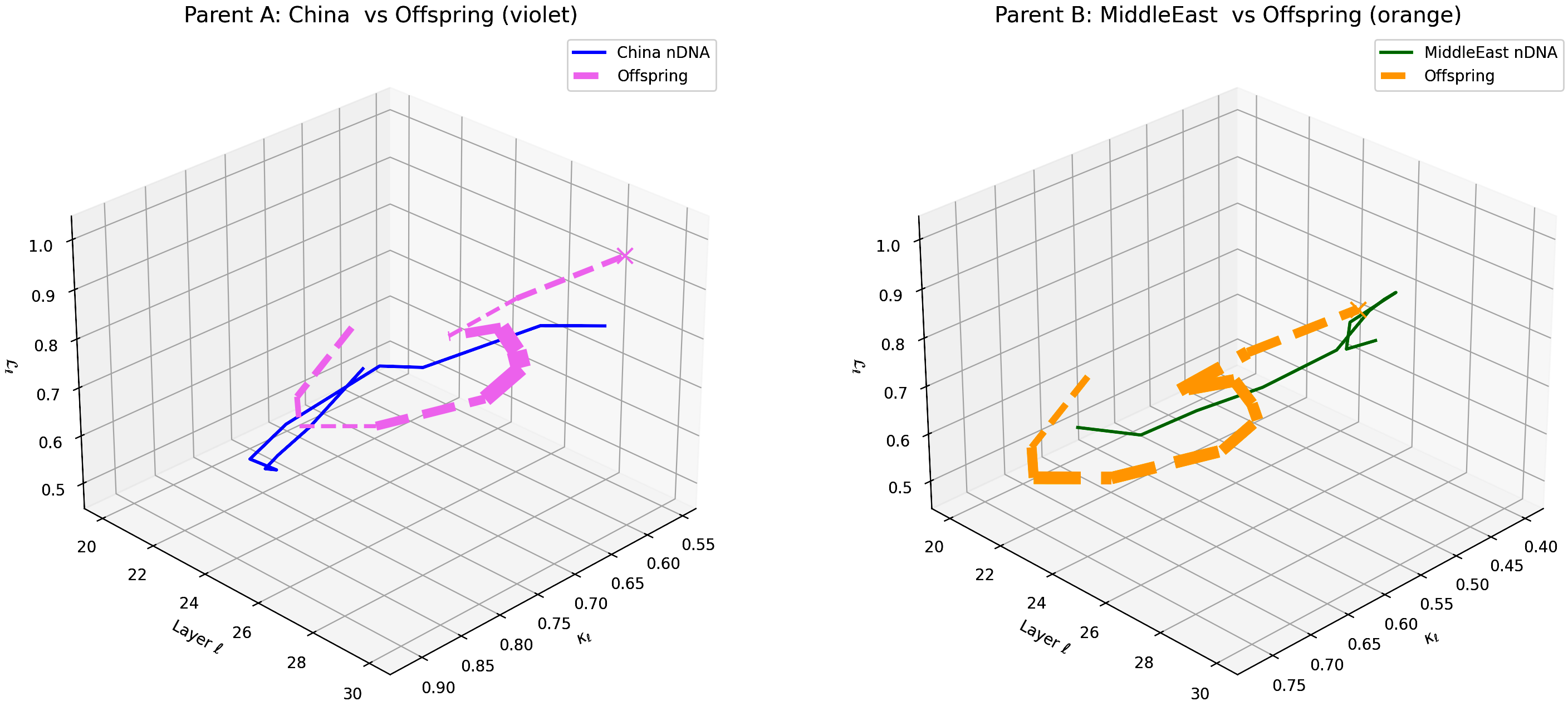
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (China, violet) and Parent B (Middle East, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory reveals a strong resemblance to Chinese semantic features in early layers (20–24) transitioning to Middle Eastern semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest promising directions for layer-wise adaptation to enhance semantic fidelity and cross-cultural generalization.
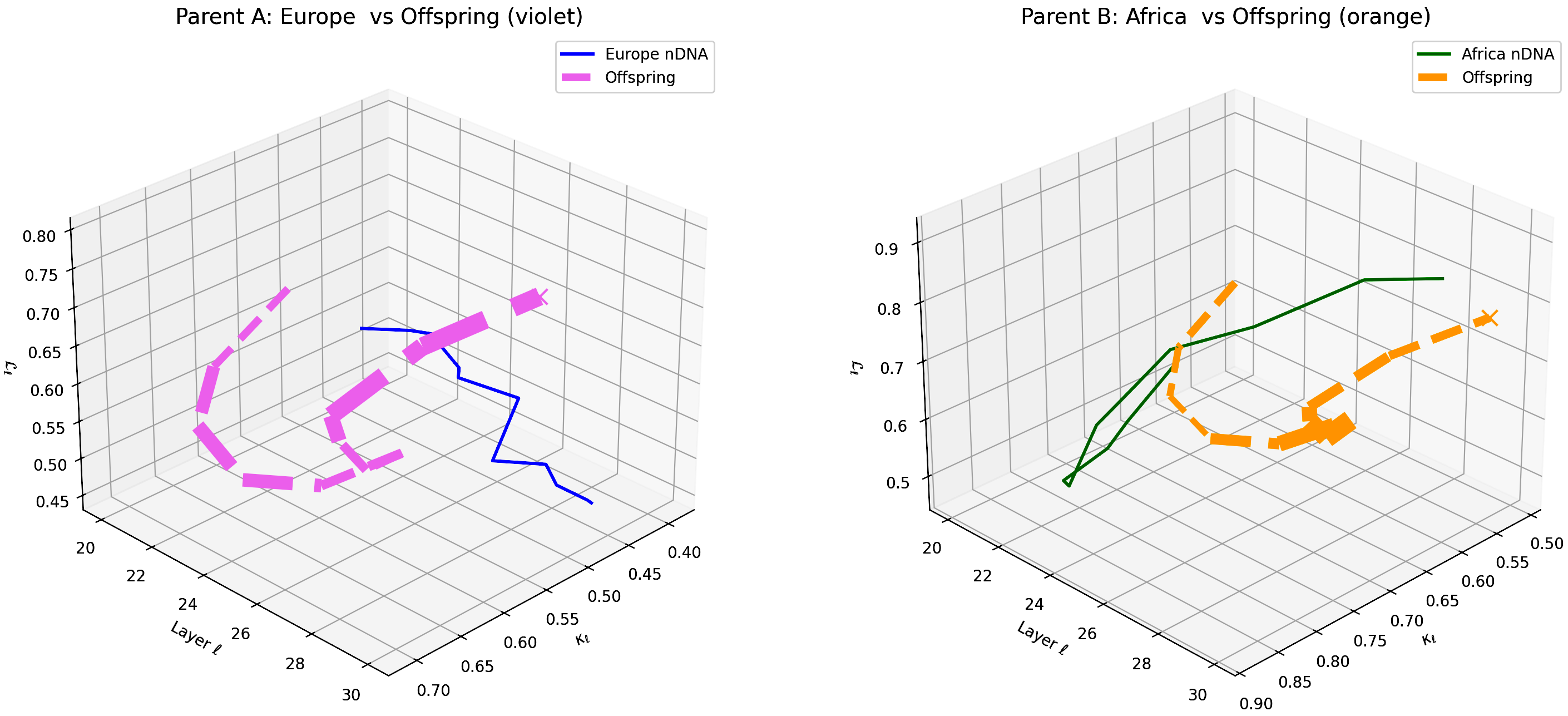
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (Africa, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory shows a notable resemblance to European semantic features in early layers (20–24) before gradually shifting toward African semantic characteristics in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest promising avenues for layer-wise adaptation to improve semantic fidelity and cross-cultural generalization.
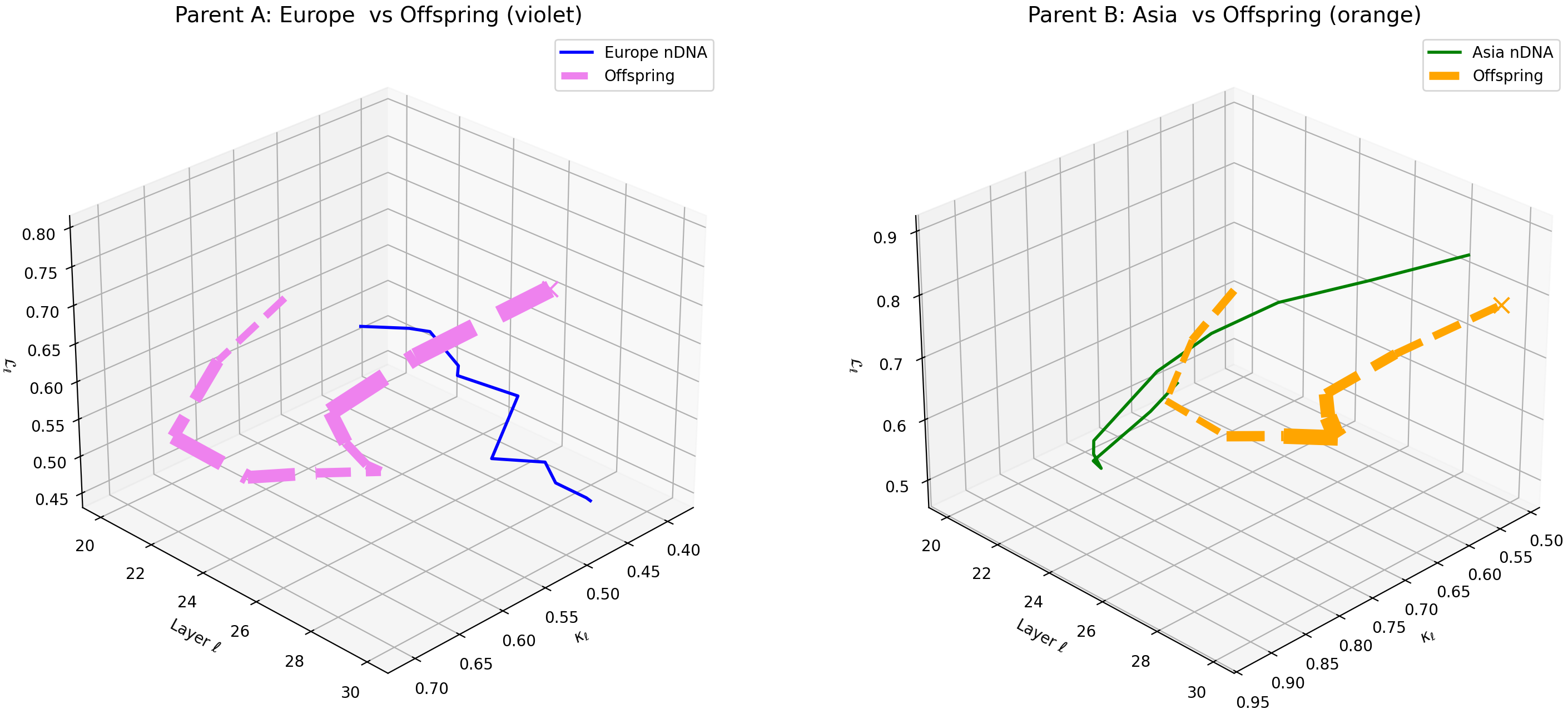
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (Asia, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a notable resemblance to European semantic features in early layers (20–24) with a gradual shift towards Asian semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest layer-wise adaptation opportunities for improving semantic fidelity and cross-cultural generalization.
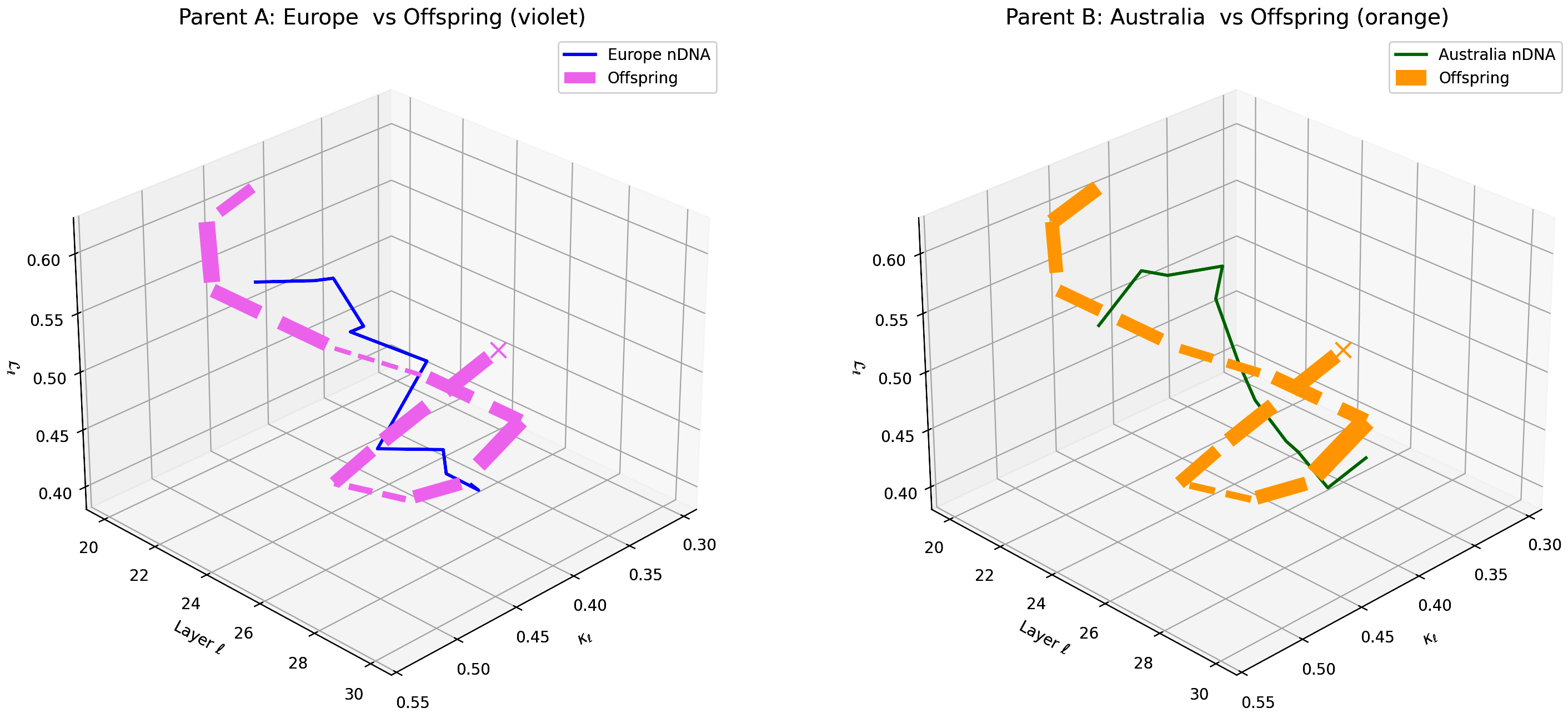
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (Australia, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a strong resemblance to European semantic features in early layers (20–24) transitioning towards Australian semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These findings suggest opportunities for layer-wise adaptation to enhance semantic fidelity and cross-cultural generalization.
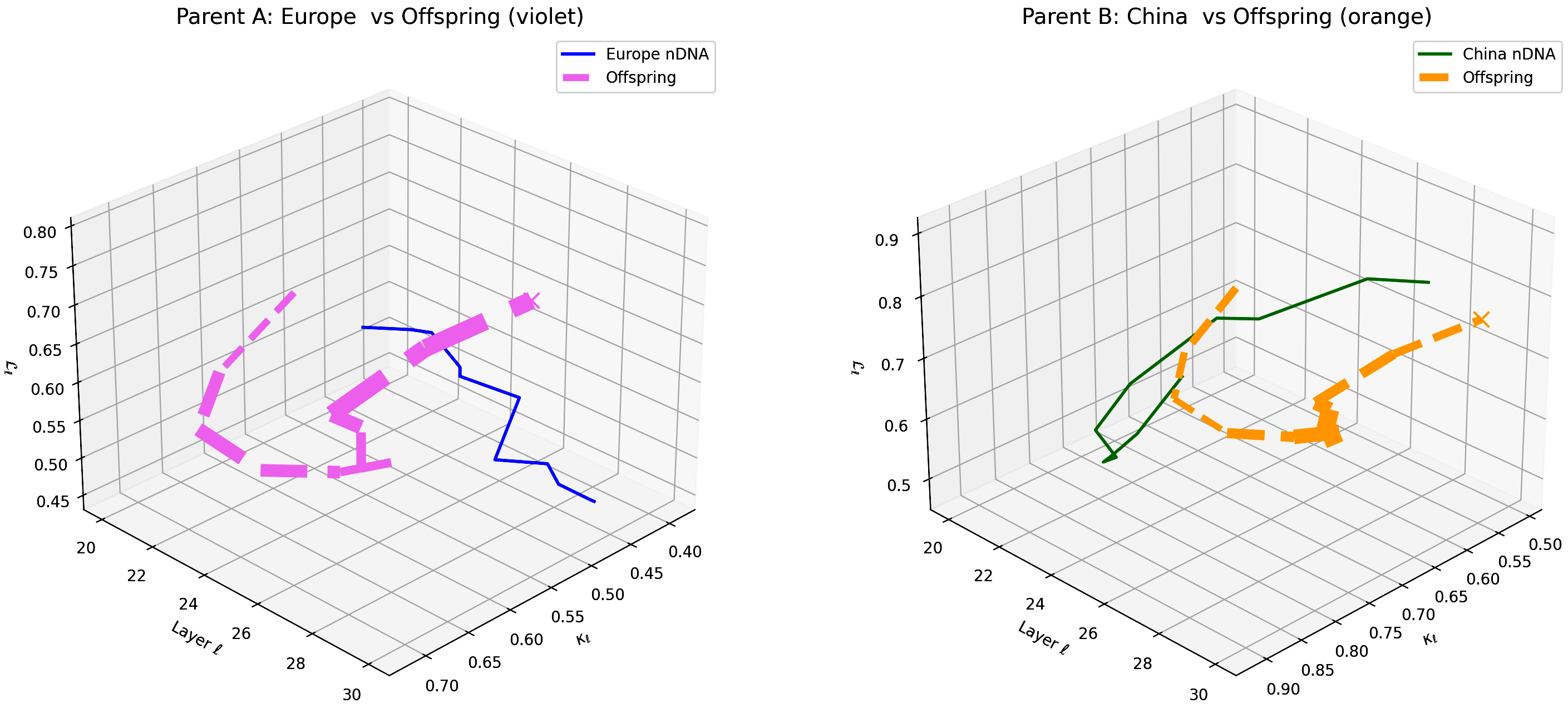
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (China, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a clear resemblance to European semantic features in early layers (20–24) and shifts gradually towards Chinese semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest promising layer-wise adaptation approaches to enhance semantic fidelity and cross-cultural generalization.
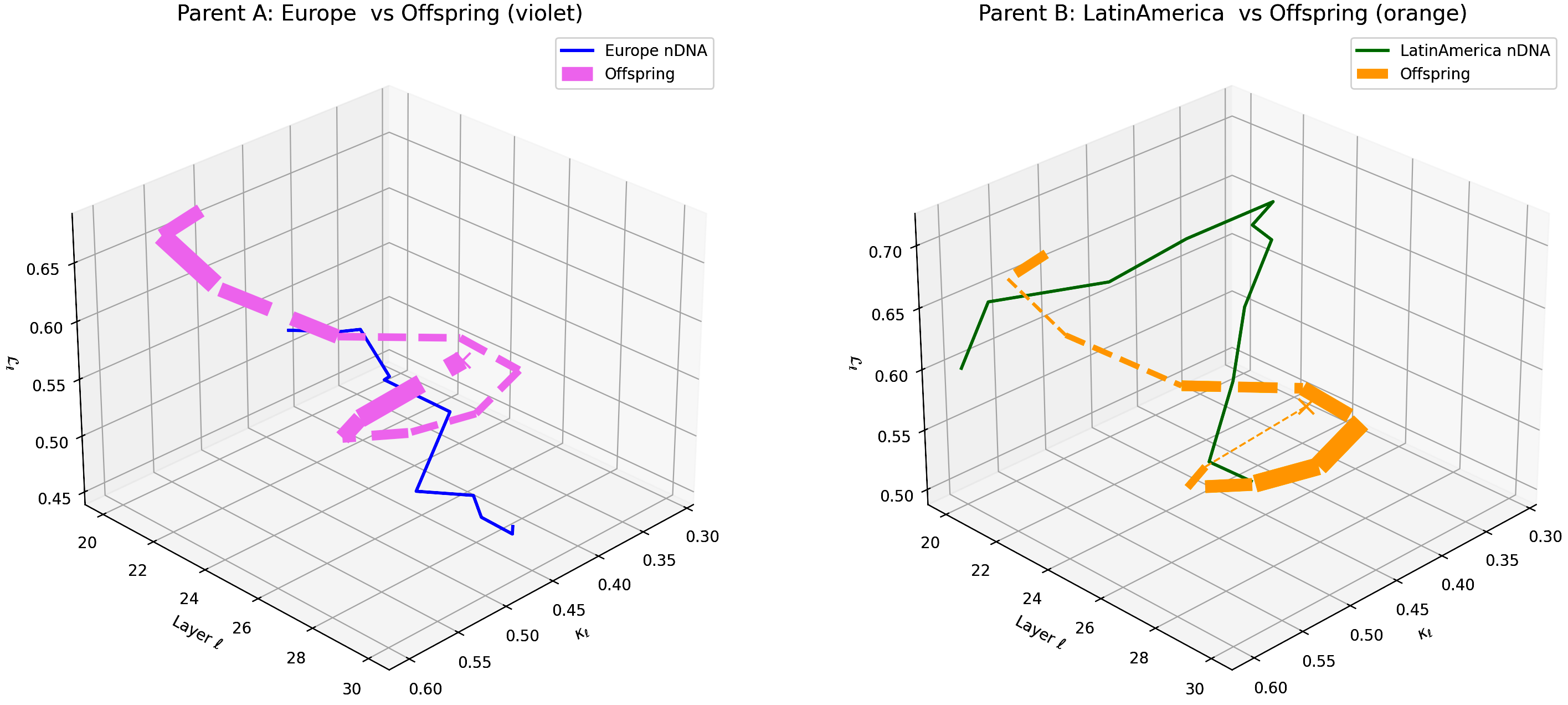
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (Latin America, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a notable resemblance to European semantic features in early layers (20–24) transitioning towards Latin American semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration of cultural priors within the offspring’s latent geometry. These insights suggest promising layer-wise adaptation approaches to enhance semantic fidelity and cross-cultural generalization.
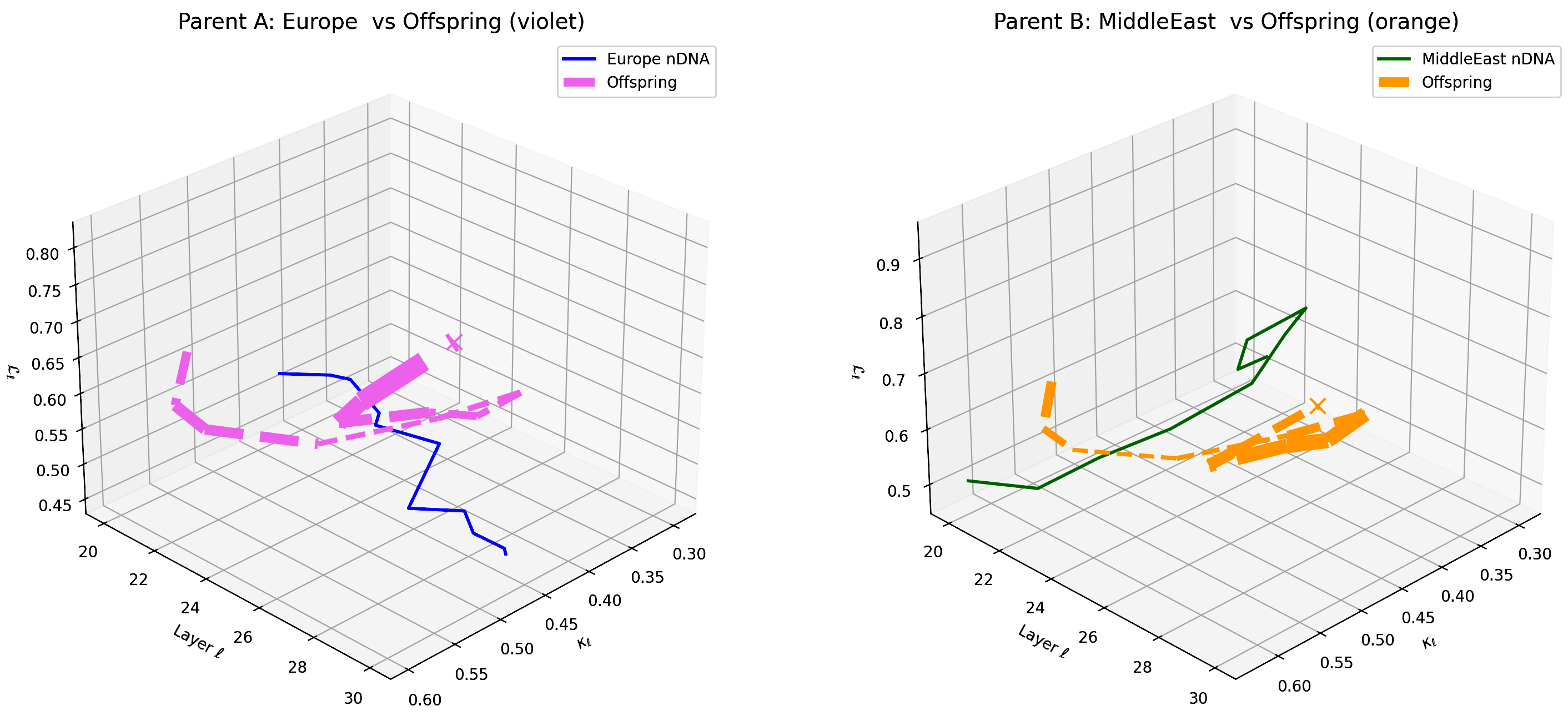
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (Middle East, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a prominent resemblance to European semantic features in early layers (20–24) and transitions towards Middle Eastern semantic traits in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern reflects the complex semantic interplay of cultural priors in the offspring’s latent geometry. These insights highlight potential layer-wise model adaptation strategies to enhance semantic fidelity and cross-cultural generalization.
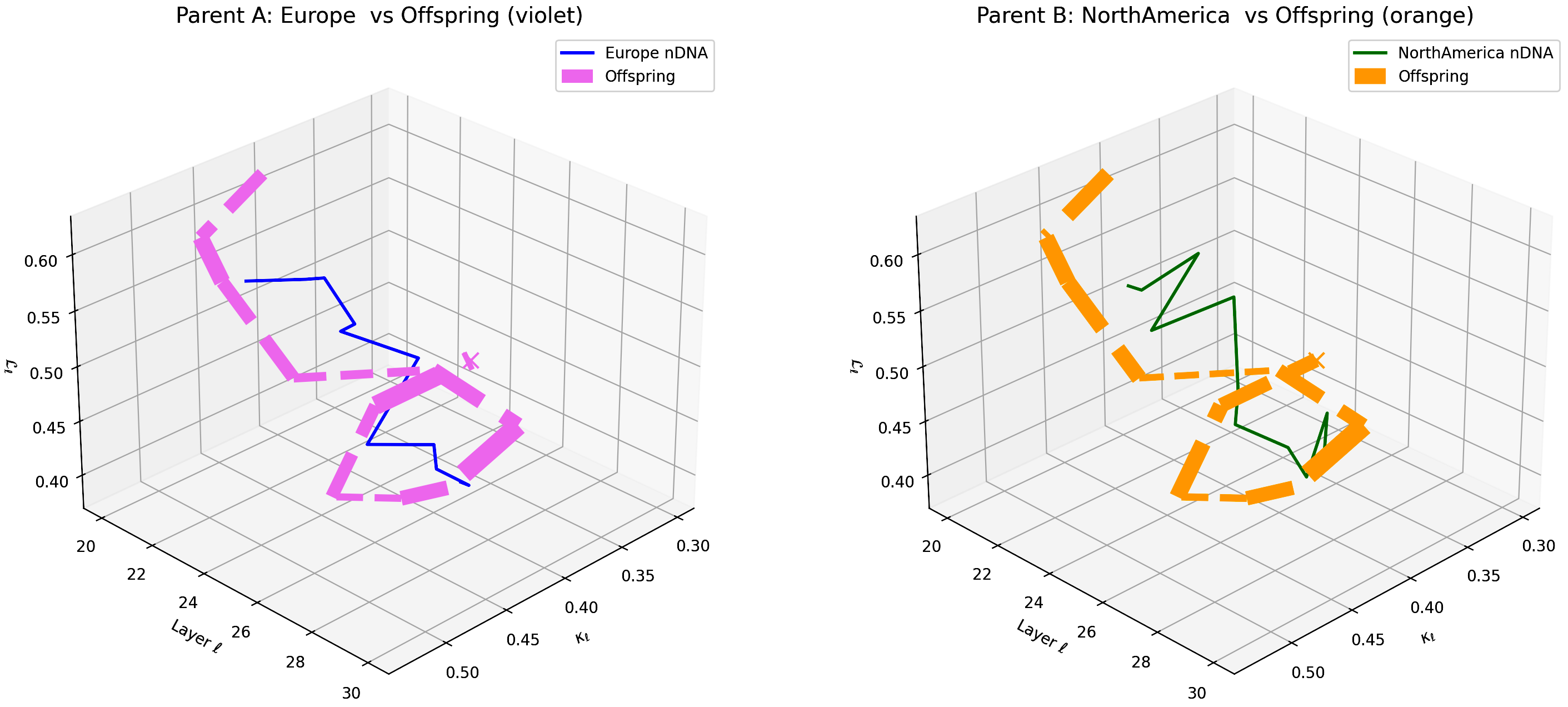
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Europe, violet) and Parent B (North America, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory demonstrates a strong resemblance to European semantic features in early layers (20–24) and shifts towards North American semantic characteristics in deeper layers (25–30), illustrating layer-dependent semantic inheritance and dominance. This pattern highlights the complex interplay of cultural priors within the offspring’s latent geometry. These insights suggest potential layer-wise model adaptation to improve semantic fidelity and cross-cultural generalization.
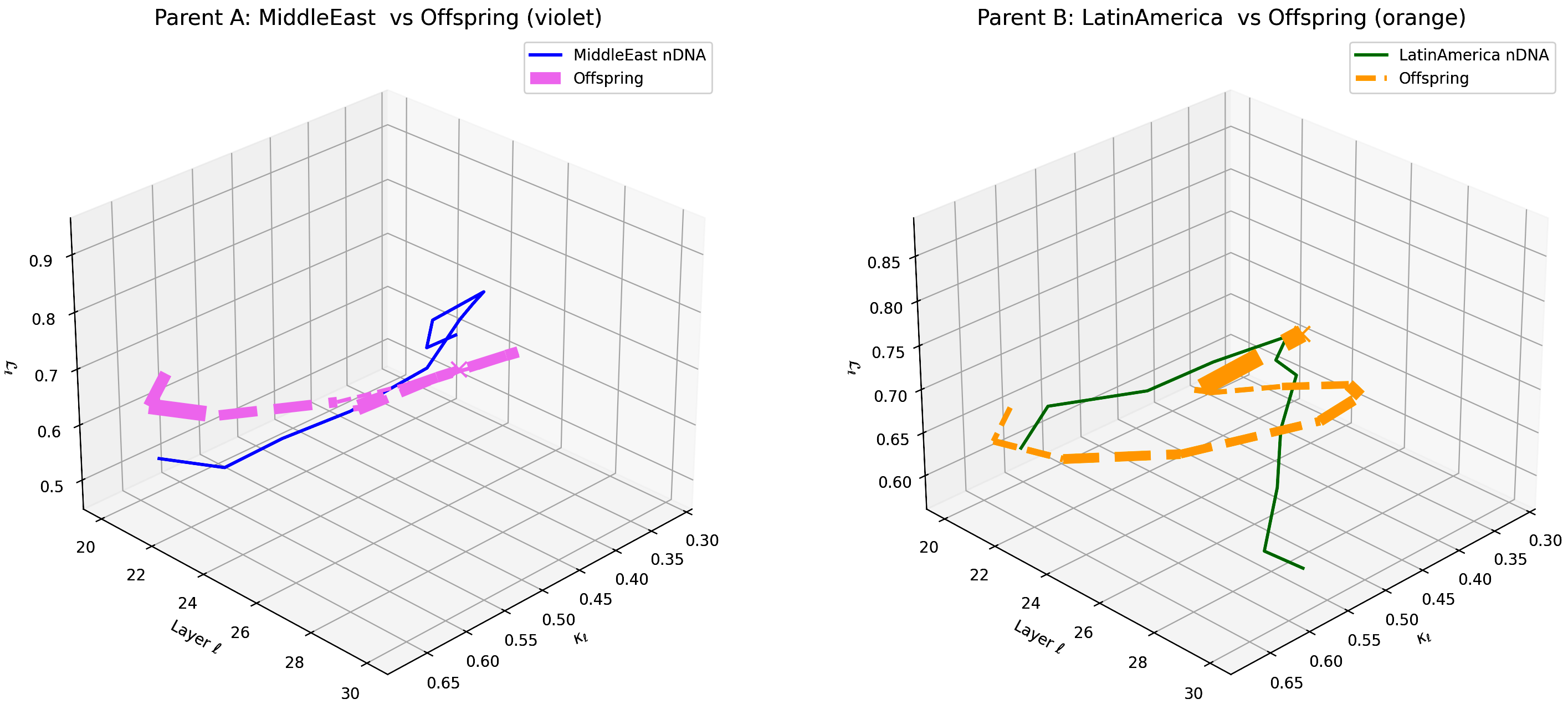
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (Middle East, violet) and Parent B (Latin America, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory displays a marked resemblance to Middle Eastern semantic patterns in early layers (20–24) and transitions towards Latin American semantic features in deeper layers (25–30), illustrating layer-specific semantic inheritance and dominance. This pattern highlights the intricate integration of cultural priors within the offspring’s latent geometry. These insights suggest opportunities for layer-targeted model adaptation to enhance semantic fidelity and cross-cultural generalization.
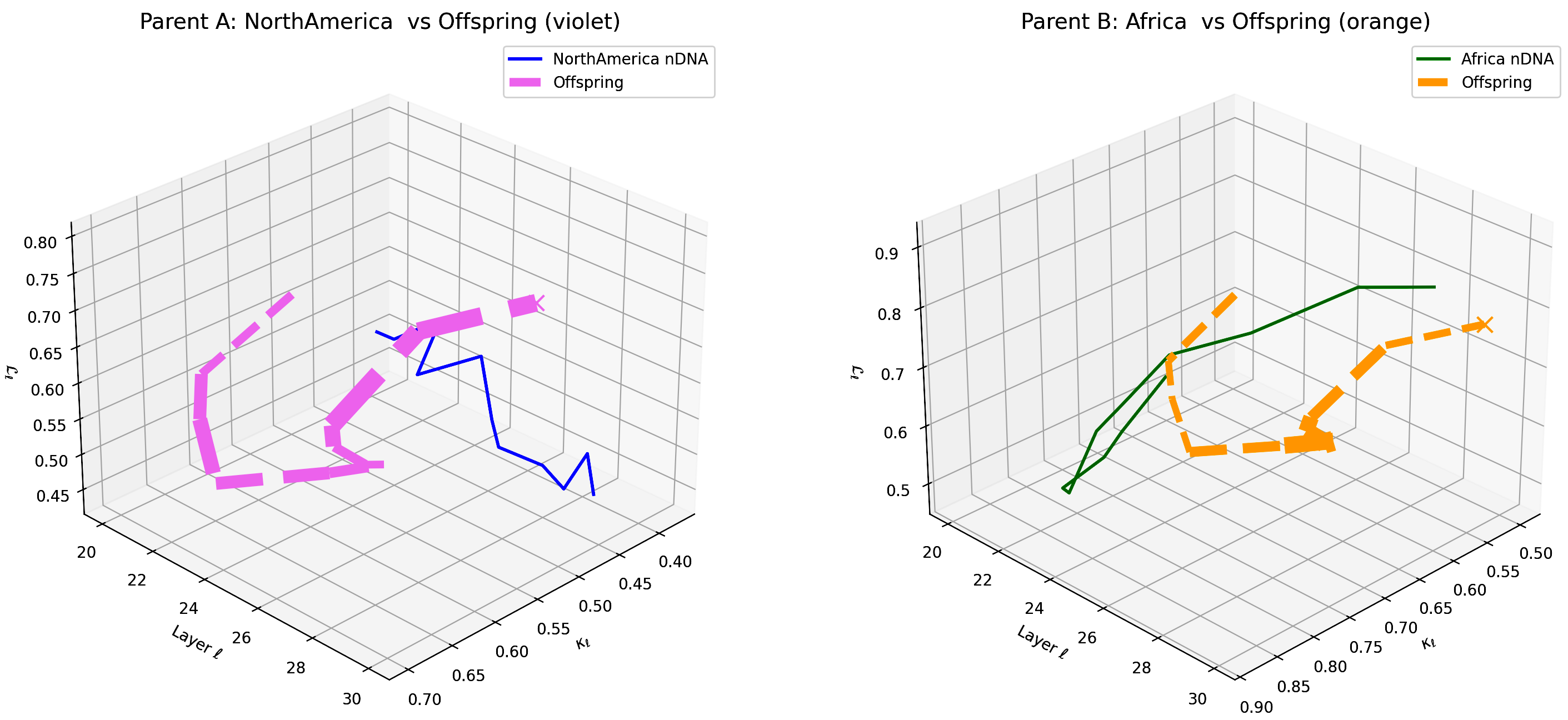
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (North America, violet) and Parent B (Africa, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a notable resemblance to North American semantic patterns in early layers (20–24) and gradually shifts towards African semantic features in deeper layers (25–30), reflecting layer-specific semantic inheritance and dominance. This pattern highlights the complex interplay and integration of cultural priors within the offspring’s latent geometry. These insights suggest avenues for layer-targeted model adaptation to enhance semantic fidelity and cross-cultural generalization.
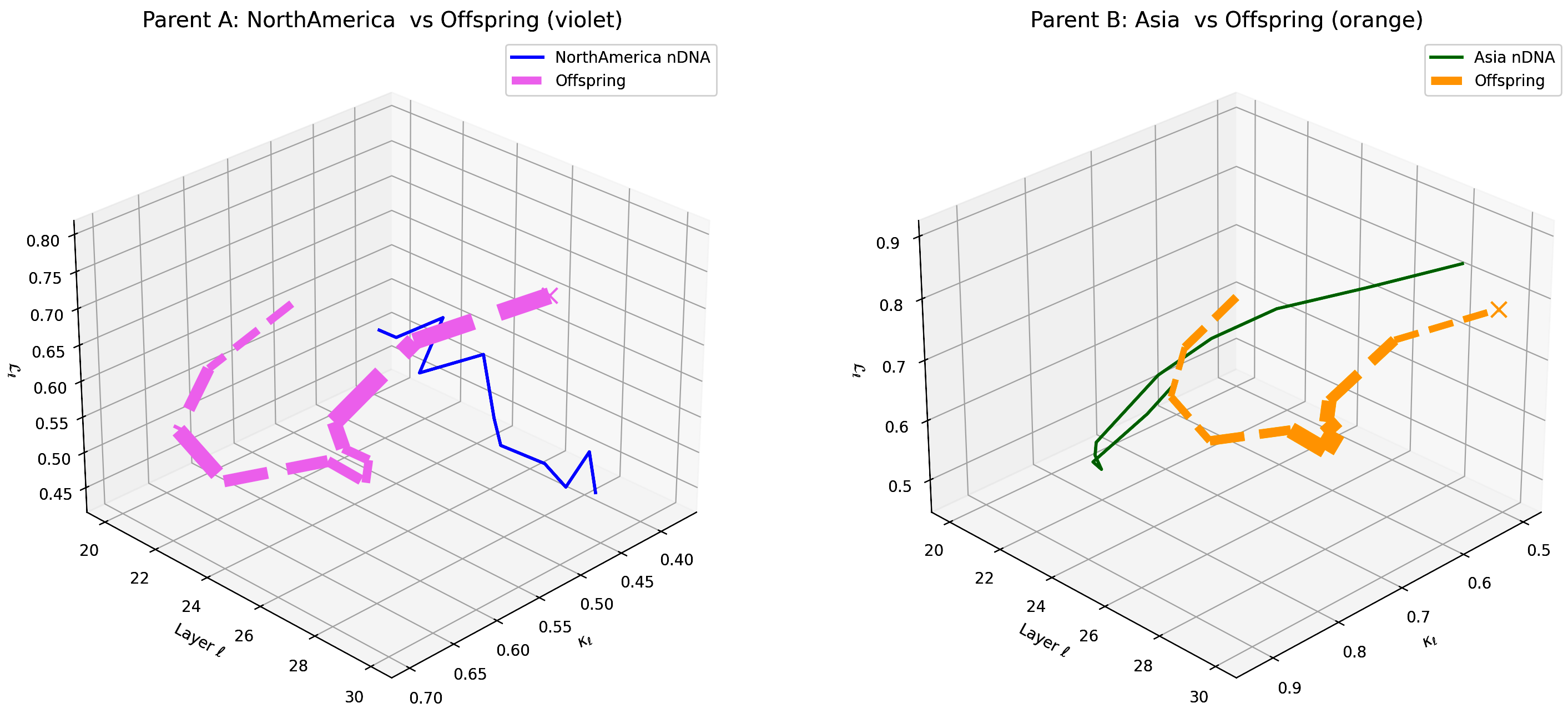
This visualization compares the offspring model’s latent geometry (thicker dashed lines) with Parent A (North America, violet) and Parent B (Asia, orange) across layers $\ell = 20$–$30$. Axes denote spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring trajectory exhibits a notable resemblance to North American semantic patterns in early layers (20–24) and transitions towards Asian semantic features in deeper layers (25–30), reflecting layer-dependent semantic inheritance and dominance. This pattern highlights the complex integration and interplay of cultural priors within the offspring’s latent geometry. These insights suggest possibilities for layer-targeted model adaptation to enhance semantic fidelity and cross-cultural generalization.
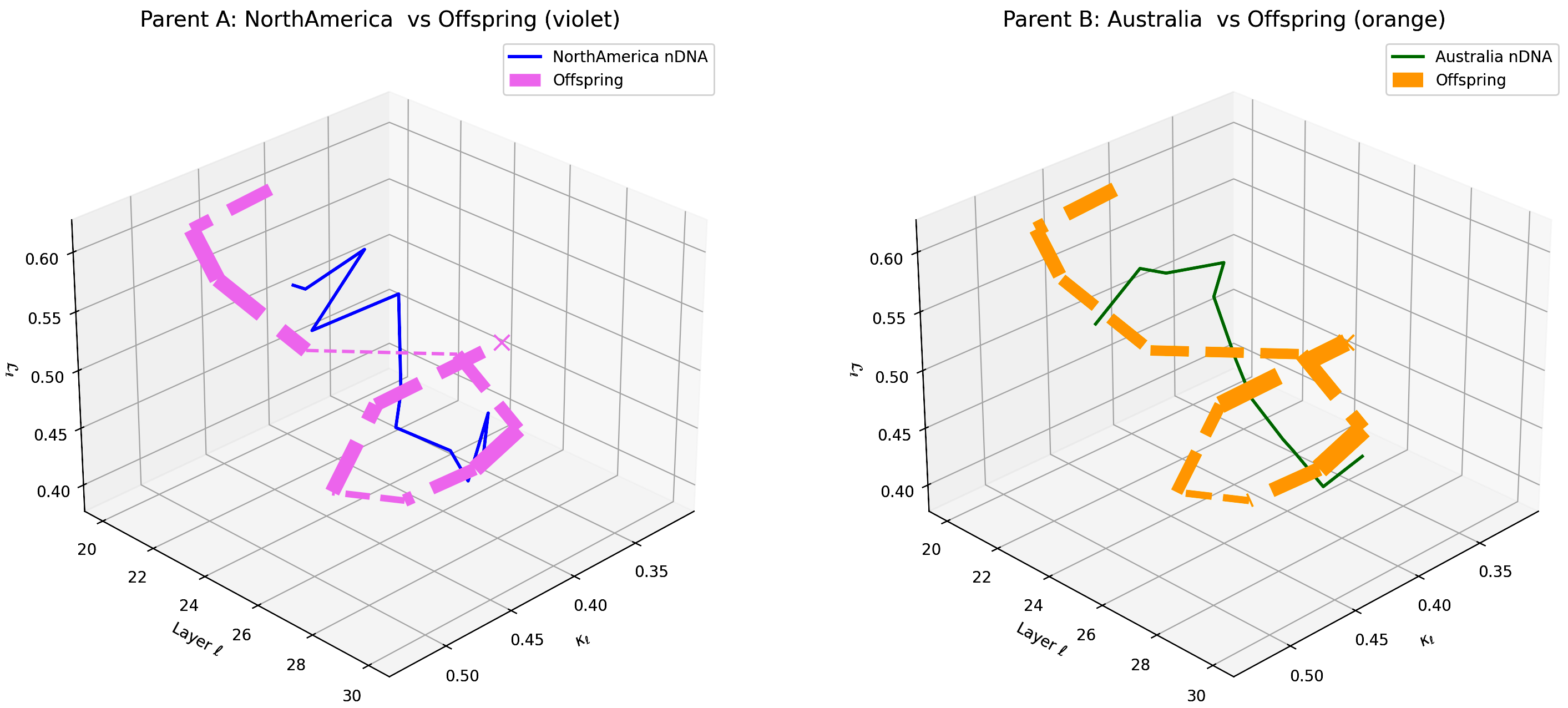
This figure compares the offspring model’s latent geometry (thick dashed magenta line) with Parent A (North America, violet) and Parent B (Australia, orange) across layers $\ell = 20$–$30$. The axes represent spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring initially aligns strongly with North American semantic priors in early layers and gradually transitions towards Australian semantic features in deeper layers, indicating layer-dependent semantic dominance shifts. This complex fusion reflects multi-layered integration of diverse cultural influences within the offspring’s latent geometry, suggesting potential for selective layer adaptation in cross-cultural model alignment and generalization.
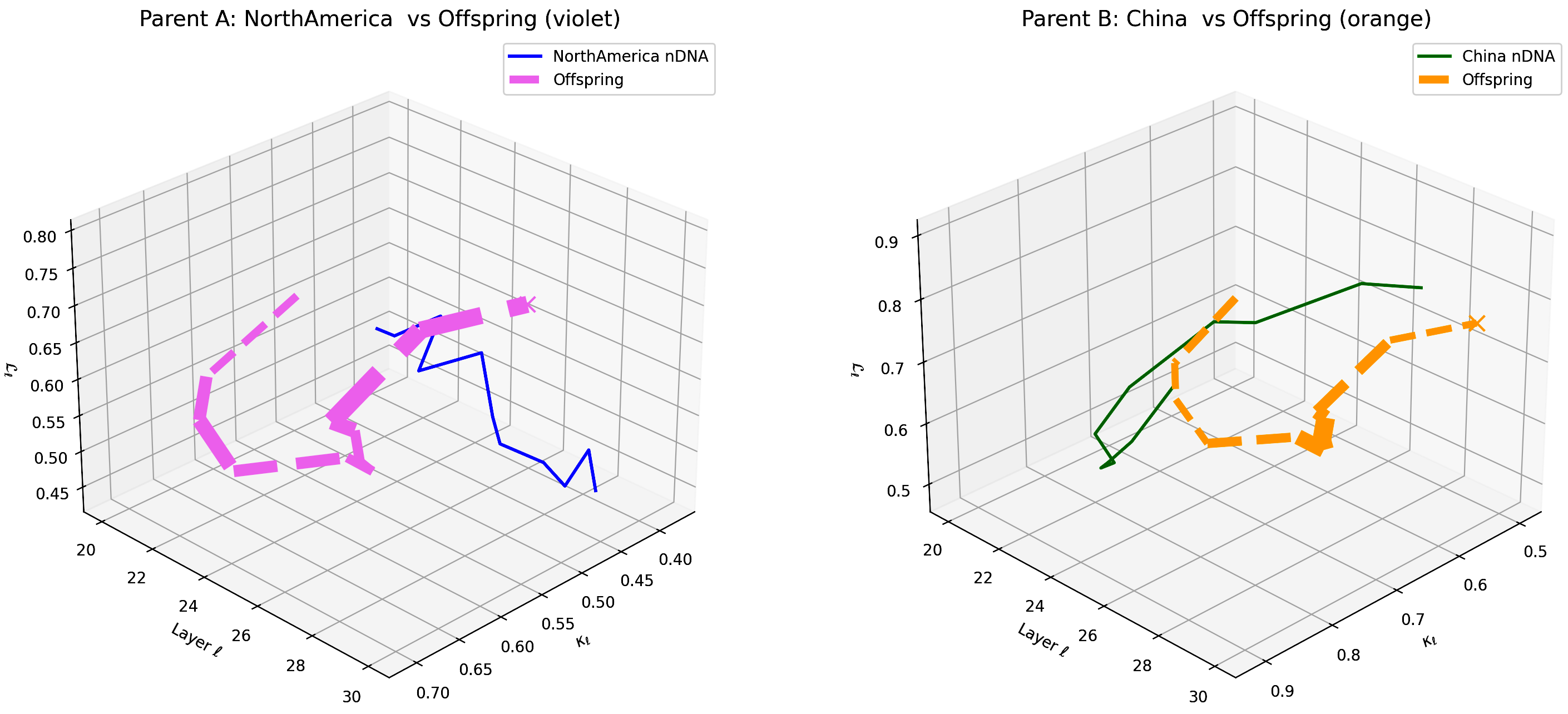
This figure compares the offspring model’s latent geometry (thick dashed magenta line) with Parent A (North America, violet) and Parent B (China, orange) across layers $\ell = 20$–$30$. The axes represent spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring initially aligns strongly with North American semantic priors in early layers and gradually transitions towards Chinese semantic features in deeper layers, indicating layer-dependent semantic dominance shifts. This complex fusion reflects multi-layered integration of diverse cultural influences within the offspring’s latent geometry, suggesting potential for selective layer adaptation in cross-cultural model alignment and generalization.
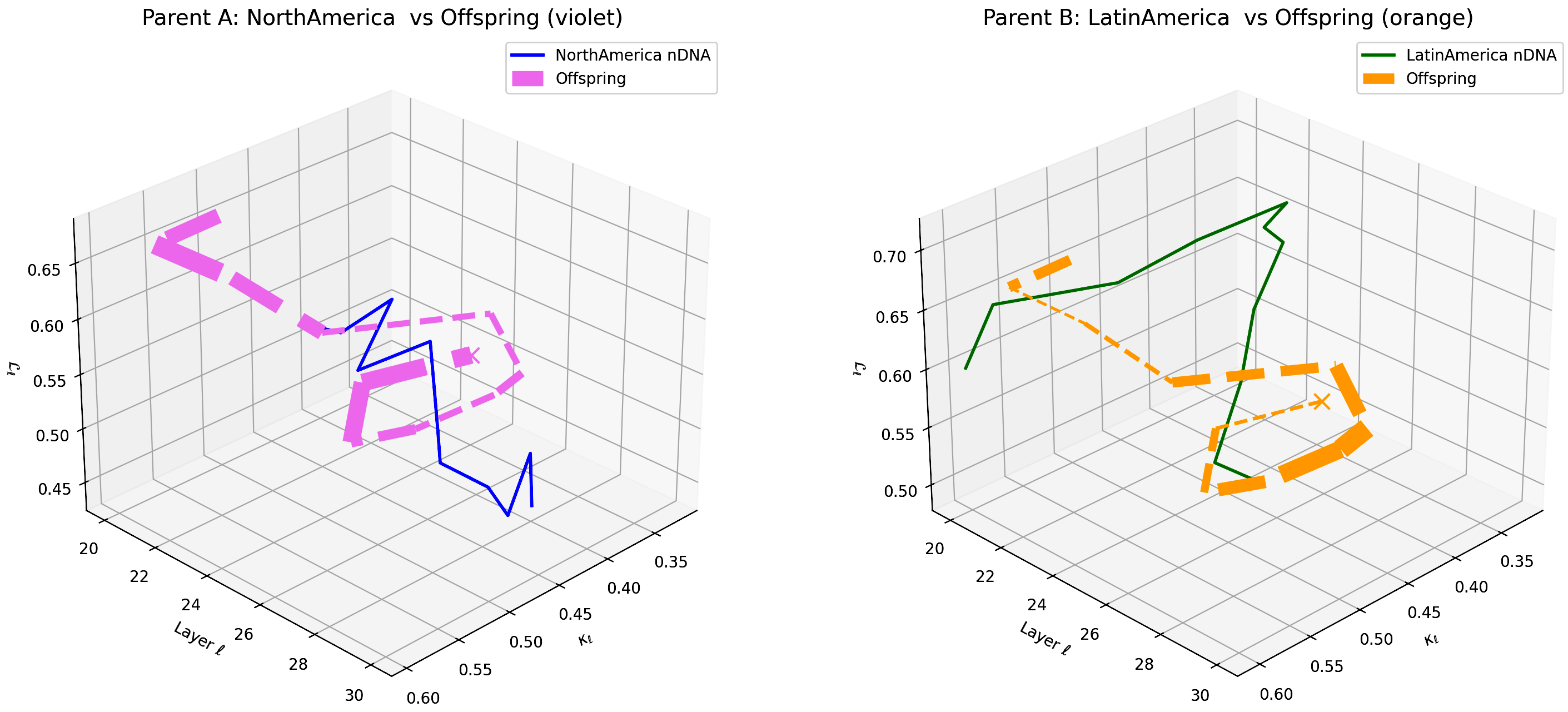
This figure compares the offspring model’s latent geometry (thick dashed magenta line) with Parent A (North America, violet) and Parent B (Latin America, orange) across layers $\ell = 20$–$30$. The axes represent spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring initially aligns strongly with North American semantic priors in early layers and gradually transitions towards Latin American semantic features in deeper layers, indicating layer-dependent semantic dominance shifts. This complex fusion reflects multi-layered integration of diverse cultural influences within the offspring’s latent geometry, suggesting potential for selective layer adaptation in cross-cultural model alignment and generalization.
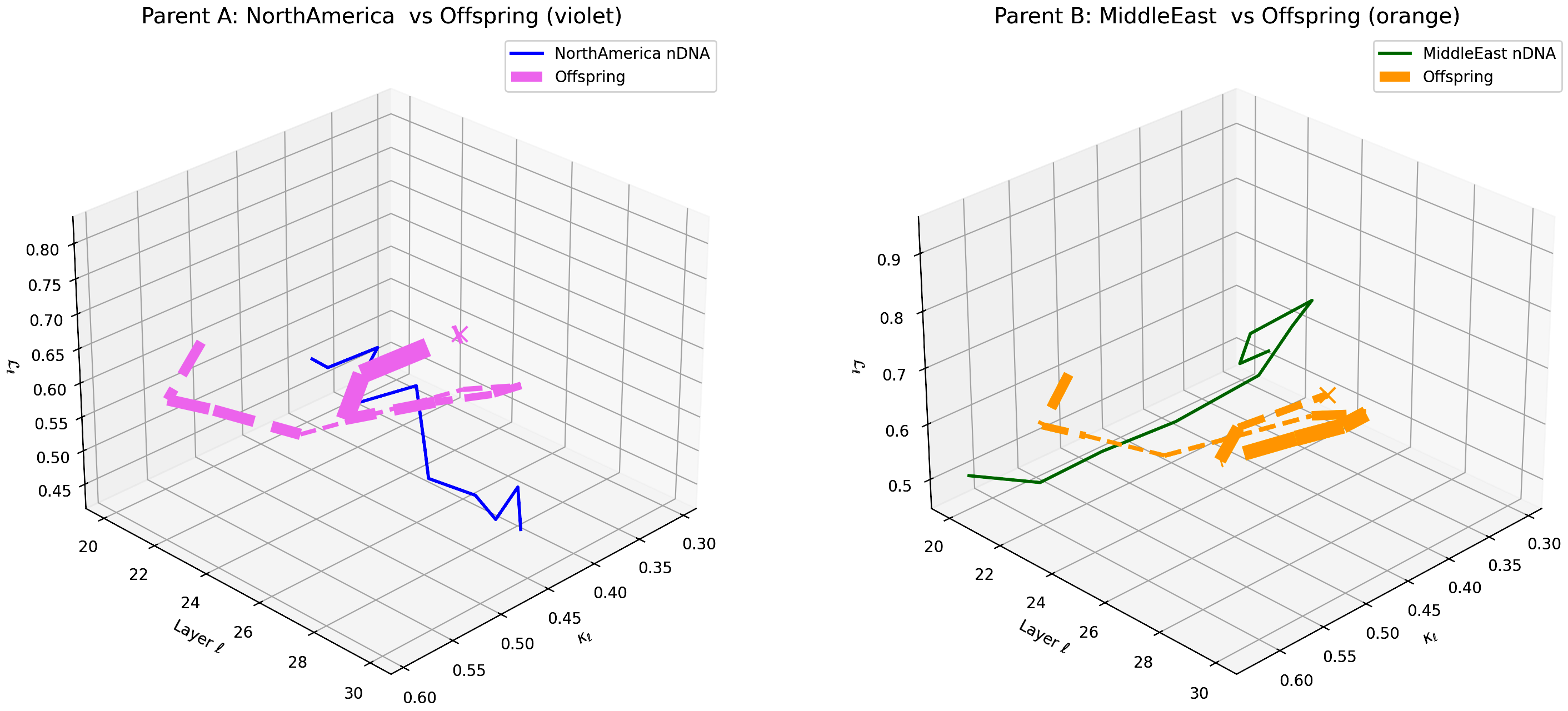
This figure compares the offspring model’s latent geometry (thick dashed magenta line) with Parent A (North America, violet) and Parent B (Middle East, orange) across layers $\ell = 20$–$30$. The axes represent spectral curvature $\kappa_{\ell}$, layer index $\ell$, and latent radius $L_{\ell}$. The offspring initially aligns strongly with North American semantic priors in early layers and gradually transitions towards Middle Eastern semantic features in deeper layers, indicating layer-dependent semantic dominance shifts. This complex fusion reflects multi-layered integration of diverse cultural influences within the offspring’s latent geometry, suggesting potential for selective layer adaptation in cross-cultural model alignment and generalization.
\[ \boxed{ M_{\text{offspring}}(\ell) = \alpha(\ell) \cdot M_A^{(\ell)} + (1 - \alpha(\ell)) \cdot M_B^{(\ell)} + \varepsilon^{(\ell)} } \]
where \( \alpha(\ell) \in [0,1] \) denotes a layer-dependent semantic dominance coefficient that dynamically shifts parental influence across model depth. The residual term \( \varepsilon(\ell) \) captures emergent nonlinear geometry beyond simple interpolation. This framework explains the observed multi-layered integration and selective semantic imprinting of diverse cultural priors in offspring latent spaces, highlighting the sophistication of cross-cultural model alignment and generalization.
References
[1] Nei, Masatoshi “Genetic distance between populations” The American Naturalist (1972).
[2] Gretton, Arthur, Borgwardt, Karsten M, and others “A kernel two-sample test” Journal of Machine Learning Research (2012).
[3] Amari, Shun-ichi “Natural gradient works efficiently in learning” Neural Computation (1998).
[4] Tenney, Ian, Das, Dipanjan, and others “BERT rediscovers the classical NLP pipeline” Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics (2019).
[5] Peyr{'e}, Gabriel and Cuturi, Marco “Computational Optimal Transport” Foundations and Trends® in Machine Learning (2019).
[6] Mackay, Trudy F.C., Stone, Eric A., and others “The genetics of quantitative traits: challenges and prospects” Nature Reviews Genetics (2009).