The Cartograph: Latent Semantic Genome of Foundation Models
Cartograph: Latent Semantic Genome of Foundation Models
Before we unveil nDNA, we must confront a foundational question: What qualifies as heritability in artificial cognition? Conventional artifacts–weights, activations, or the output behavior–are mere epiphenomena of training. In contrast, nDNA seeks to capture a model’s semantic genome: the latent organizational structures that govern how knowledge is internally represented, adapted, and transmitted across fine-tuning, distillation, pruning, and deployment. To chart the semantic ancestry of AI systems, we must move beyond output-level metrics and embrace a deeper epistemic foundation–one that traces not just what models say, but how they reason, evolve, and remember. We argue that nDNA constitutes this missing genomic trace: a structured latent fingerprint of artificial cognition. Just as molecular genetics enabled biology to transcend surface taxonomies and uncover causal mechanisms, we contend that a genomic lens is now essential for machine learning–one that can quantify:

Layer Importance and Semantic Specialization: Not all layers contribute equally to a model’s epistemic structure. A growing body of evidence [1, 2, 3, 4] reveals that semantic representations, cultural memory, and alignment behavior disproportionately concentrate in the mid-to-upper transformer layers–particularly the final 10 layers in ~30-layer models. These layers encode more than surface patterns; they carry deep semantic priors and value shifts induced by alignment, fine-tuning, and cultural adaptation. For nDNA to serve as a meaningful genomic diagnostic, it must trace inheritance, drift, and trait transformation across these epistemically sensitive regions.
Semantic Drift and Heritable Traits: Subtle misalignments and persistent divergences–documented in alignment studies [5, 6]–can occur even when models appear behaviorally consistent. These are not superficial perturbations but inheritable epistemic traits passed along neural offspring [7, 8].
Value Simulation vs. Internalization: As models grow more context-sensitive, they learn to simulate alignment without embodying its values [9, 10]. Disentangling true normative internalization from strategic mimicry is essential for any meaningful epistemic inspection.
Plasticity and Collapse: Aggressive fine-tuning, distillation, or ideological merging can induce plasticity collapse–a reduction in epistemic flexibility and semantic richness [11, 12]. This demands metrics that trace both robustness and degeneration over time.
Latent Cultural Conflict: In multilingual or cross-cultural settings, models often encode conflicting or incoherent value systems [13, 14]. These conflicts are not visible through BLEU or ROUGE–they reside in the model’s latent belief structure and must be surfaced through geometric lineage analysis.
Topological Continuity: Alignment and fine-tuning warp the internal geometry of models in nontrivial ways [15, 4]. nDNA must preserve continuity and interpretability of trajectories across such transformations.
Epistemic Mutation: Merging preferences, annotator distributions, or learned behaviors–as explored by [16]–creates emergent traits that standard metrics cannot track. These mutations are only diagnosable through a genomic lens on representation evolution.
nDNA empowers us to interrogate the hidden geometry of learning–revealing how foundational operations such as alignment, fine-tuning, quantization, pruning, and multilingual fusion subtly but systematically reshape a model’s semantic core. It uncovers cultural instabilities introduced through regional adaptation, traces asymmetric inheritance patterns across neural offspring, visualizes latent reorganizations induced by merging or distillation, and quantifies a model’s capacity to resist or absorb conflicting epistemic pressures.
These phenomena–often dismissed as quirks–are in fact heritable traits, etched into the model’s internal manifold. When viewed through this lens, model collapse, alignment-induced drift, and semantic mimicry cease to be incidental failures and instead emerge as structural signatures of deeper latent dynamics. nDNA thus transcends metaphor to become a scientific grammar for measuring epistemic resilience, semantic coherence, cultural consistency, and trait inheritance–offering a principled lens through which to govern, understand, and audit the evolving anatomy of artificial cognition.
We further posit that cultural provenance induces a distinct layerwise calibration effect, predominantly localized in the final decoder layers \(\ell \in [20, 30]\), where sociolinguistic priors exert the strongest influence on output distribution. To capture this, we introduce the nDNA Score–a composite diagnostic unifying: (i) Spectral curvature \(\kappa_\ell\), reflecting the compression and warping of conceptual flow; (ii) thermodynamic length \(\mathcal{L}_\ell\), quantifying the epistemic effort required to traverse belief transitions; and (iii) the norm of the Belief Vector Field \(\lVert\mathbf{v}_\ell^{(c)}\rVert\), measuring the directional intensity of latent cultural drift.
Together, these dimensions form a latent semantic fingerprint–a high-dimensional, biologically inspired signature of internal cognition–enabling us to trace, compare, and govern the neural evolution of foundation models with unprecedented granularity.
Rationale and Formalization: Why Trajectories, Not Weights
The usual levers for interpreting and governing LLMs—parameter counts, sparsity patterns, attention heatmaps—live in coordinates that are non-identifiable and only weakly tethered to deployed behavior. Permutations, rotations, and low-rank re-expressions can leave the realized function intact while scrambling weight-level narratives [17, 18, 19, 20, 21, 22]. By contrast, what remains stable under such reparameterizations is the on-input computation: for a prompt x, the forward pass traces a trajectory of hidden states through depth. Endowing representation space with information geometry (e.g., Fisher–Rao pullbacks) yields coordinate-free notions of distance, bending, and effort that track changes in the output law [23, 24, 25]. We read this as semantic hydrodynamics: meaning is transported through layers like a fluid through a shaped conduit.
Limits of weight-space and attention views
Weight-space indicators (parameter counts, sparsity, individual neurons/heads) live in non-identifiable coordinates: permutations, rotations, or refactorings can leave behavior unchanged while rewriting any weight-level narrative. Attention maps are largely descriptive, not reliably causal or stable—different patterns can yield the same outputs and head roles drift across training. These limits motivate a behavior-first, coordinate-free view that reads the model’s on-input trajectory of representations, rather than static weights or raw attention.
Weight space is non-identifiable and behavior-misaligned. Permutation symmetries, rotations, and low-rank re-expressions can preserve the function while scrambling weight-level narratives. Empirically, independently trained solutions are often mode-connected by low-loss paths or become connected after accounting for permutations, undermining explanations that cling to specific coordinates [17, 18, 19, 20, 21]. Moreover, practical levers like weight averaging/model soups alter parameters while leaving deployed behavior similar or improved, again decoupling “where weights sit” from what the model does [22]. In short, we deploy behaviors, not weights; coordinate-specific stories are fragile.
Attention is informative but not a faithful, stable mechanism by itself. Extensive tests show that similar outputs can arise from disparate attention patterns, and directly perturbing attention often leaves predictions largely unchanged; hence attention weights are, at best, descriptive [26, 27]. Redundancy and role-drift are common: many heads can be pruned with little loss, a few heads do the “heavy lifting,” and head functions shift across training or fine-tuning, weakening governance value of raw maps [28, 29, 30, 31]. Post-hoc corrections (e.g., attention flow/rollout) improve alignment with token importance but still treat attention as signals, not ground-truth causes [32]. Beyond attention, critical computation lives in MLPs: feed-forward layers behave like key–value memories that store and retrieve factual associations, so attention alone under-specifies mechanism [33]. Methodologically, the broader saliency literature warns that visually plausible explanations can fail sanity checks, and “faithfulness” must be defined and evaluated explicitly [34, 35].
What is stable: the on-input trajectory. For each prompt x, the forward pass traces a depth-indexed path of hidden states—the operational object we actually deploy. Prior analyses show that linguistic competencies emerge layerwise in consistent pipelines (POS → parsing → NER → SRL → coreference), supporting the intuition that the trajectory through representation space is a robust behavioral signature [36, 30]. This motivates nDNA’s choice to work in trajectory space, not parameter space.
We read AI foundation models as semantic fluid–dynamics
nano-gpt (structure). Architecture as channel blueprint: depth acts like the axial coordinate; residuals $\leftrightarrow$ bypass pipes; attention / MLP blocks act as mixers/valves that locally reshape the flow of representations.
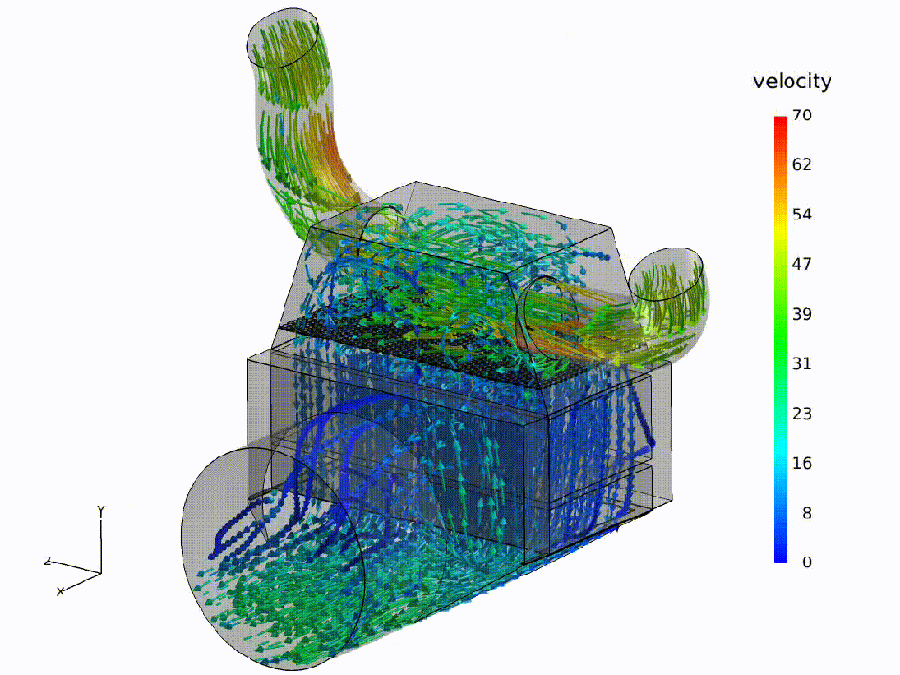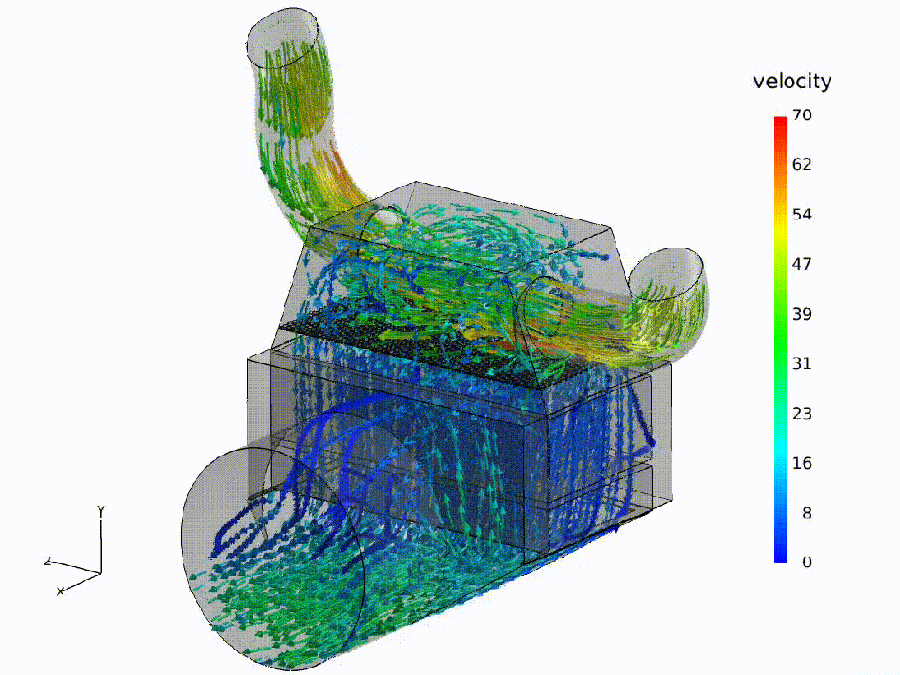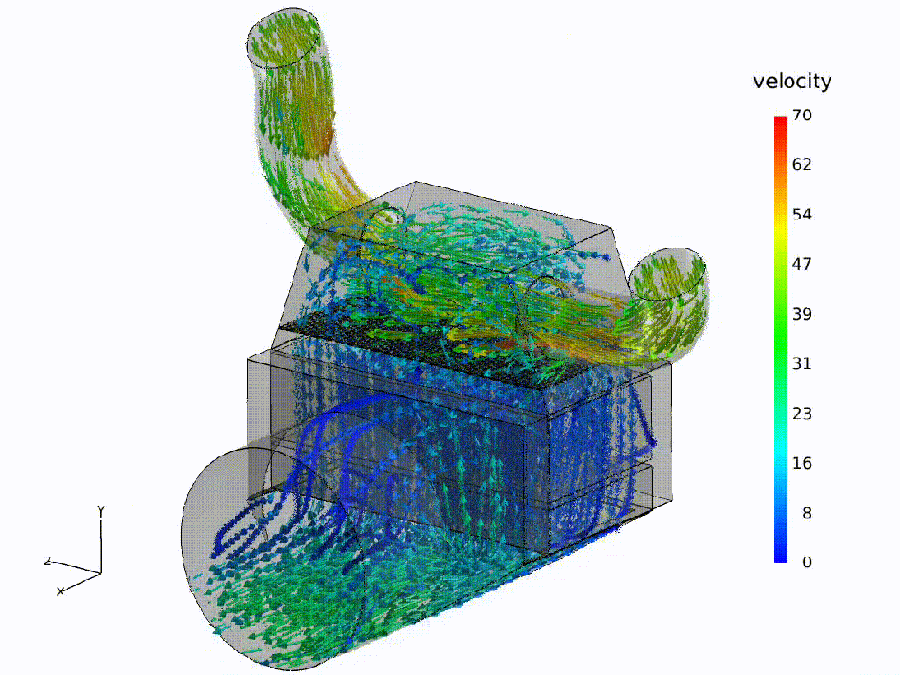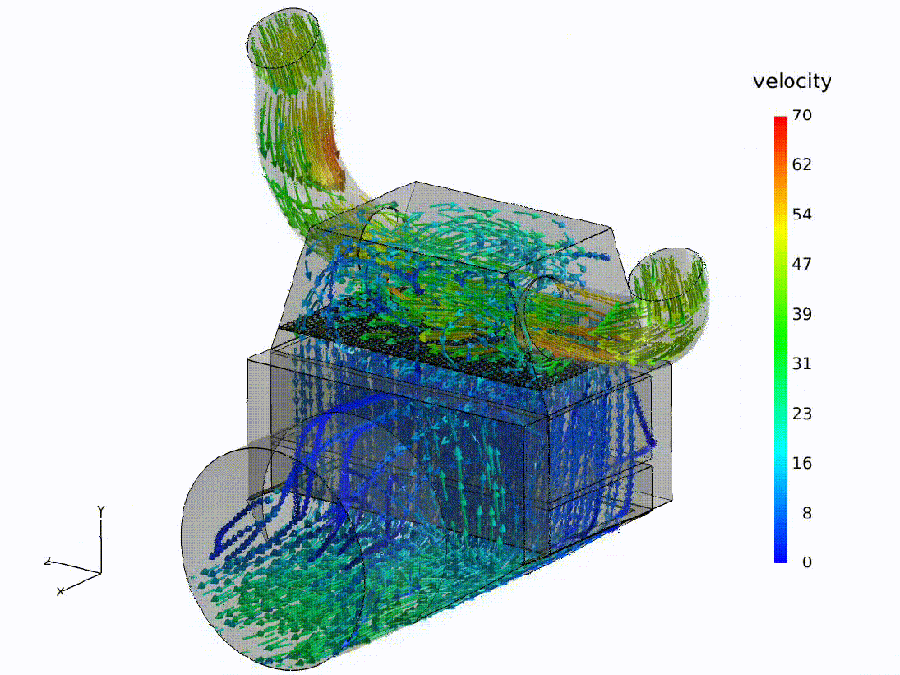
Flow simulation (analogue). Fluid: colored streamlines show speed through a bend and throat—curvature rises, shear increases, small recirculation pockets may form. Semantic: bends $\Rightarrow$ spectral curvature spikes ($\kappa$); constrictions $\Rightarrow$ thermodynamic length bursts ($\Delta L$); eddies $\Rightarrow$ local rotation in the belief field ($\nabla\times\mathbf{v}$).

Pipeline metaphor (macro view). Geometry governs transport: routing capacity and effort depend on the network of ducts. Semantic: model design / fine-tuning shapes where meaning flows easily, where it pays, and where it recirculates.
Semantic hydrodynamics. Model. We read the forward pass as semantic hydrodynamics: a prompt injects semantic mass that is transported through depth like a fluid through a shaped channel. Why. Weight/attention coordinates can change without altering behavior; the on-input flow provides behavior-first, coordinate-free signals. Reading guide. Bend $\to$ spectral curvature $\kappa$ (sharp reroutes vs. laminar refinement); Pay $\to$ thermodynamic length $L$ (where the model expends effort; $\Delta L$ bursts mark bottlenecks); Push $\to$ belief field $\mathbf{v}$ (direction/magnitude of local drive; eddies indicate recirculation). Benefit. The same metaphor specifies where to measure—bends, throats, and eddies—turning inner computation into actionable diagnostics and governance thresholds.
Why semantic hydrodynamics matters
-
We govern behavior, not coordinates. Operational concerns—robustness, safety, bias, faithfulness—attach to what the model does on an input, not to how its weights are labeled. Two checkpoints can behave the same while their parameters and attention differ. In short: the weights are the map; the trajectory is the territory.
-
Invariance beats introspection. Coordinate-bound stories change under neuron permutations, subspace rotations, or low-rank refactorings; the path an input carves and its geometry (length, curvature, alignment) are invariant because they are measured by how predictions would change, not by which index moved.
-
Geometry turns cognition into observables. An information metric acts as local stiffness: soft directions barely affect the output; stiff directions swing the predictive law. With that ruler, we quantify how far the model travels to reshape belief (thermodynamic length L), where it turns its internal argument (spectral curvature κ), and what pushes change locally (belief field v) [37, 38].
-
The hydrodynamics metaphor is operational. Like fluid in a channel, semantic flow shows corners, constrictions, and eddies: sharp bends $\Rightarrow$ high $\kappa$; narrow throats $\Rightarrow$ bursts in $\Delta L$; local recirculation $\Rightarrow$ rotational structure in $\mathbf{v}$. These are measurable, per-layer signals on the actual computation.
What this buys us (concrete payoffs).
-
Behavior-first invariance. Reading $\kappa$, $L$, and $\mathbf{v}$ on the trajectory yields fingerprints that are comparable across models, seeds, and checkpoints—even when weights or head roles reshuffle.
-
Local diagnostics. $\kappa$ spikes flag brittle decision pivots; $\Delta L$ bursts expose capacity bottlenecks or lossy transformations; low alignment (small $\cos\theta$ between $\mathbf{v}$ and the tangent $\mathbf{T}$) marks layers that move without updating belief (staging or detours).
-
Governance hooks. Geometry budgets and thresholds—max $\kappa$, allowable $\Delta L$ per slice, minimum alignment—become pre-release gates; nDNA fingerprints support drift monitoring after fine-tuning, pruning, quantization, or alignment.
-
Comparative forensics. Because $\kappa/L/\mathbf{v}$ are tied to the output law, we can attribute performance deltas to where in depth the flow changed (e.g., a new bend from fine-tuning, an effort spike from quantization) instead of to unstable weight indices.
Rule of thumb: If the goal is to explain, compare, or govern deployed behavior, analyze the flow of meaning that the input actually experiences. In nDNA: curvature says where it bends, thermodynamic length says how much it pays, and the belief field says what pushes it—all with a ruler calibrated to the model’s own predictions.
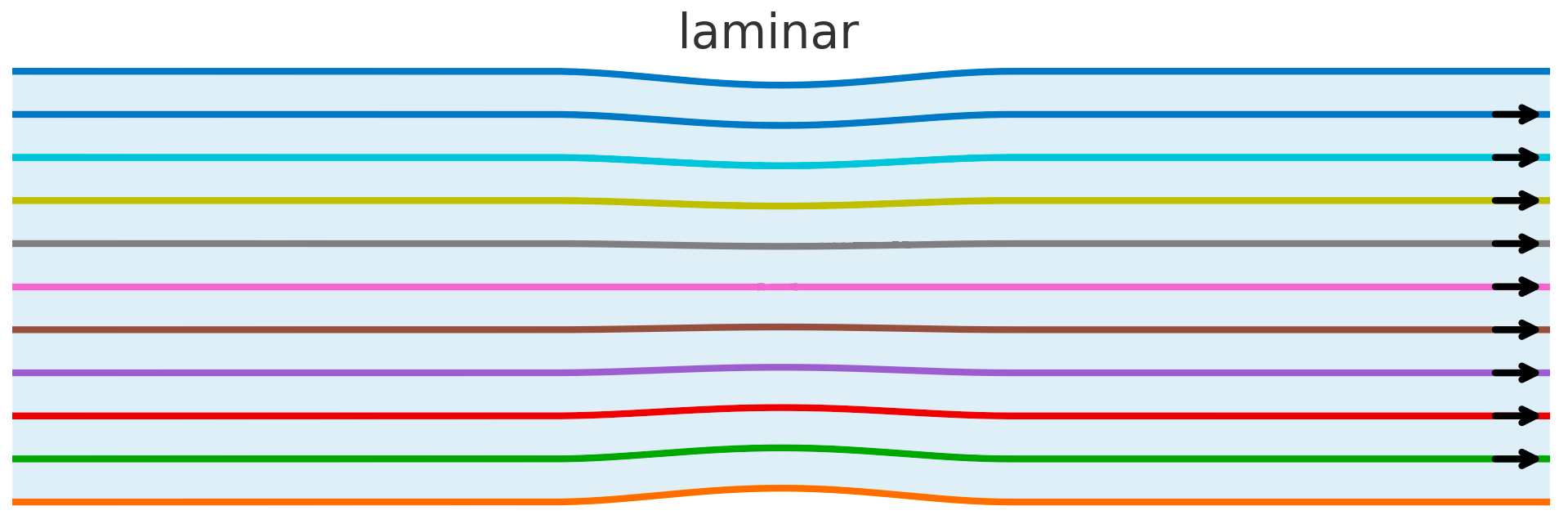
Laminar flow. Fluid: viscous–dominated, low–Re regime; nearly parallel streamlines, negligible cross–stream mixing, no recirculation.
LLM Semantic Flow: uniformly low spectral curvature $\kappa$, small steady $\Delta L$, and high alignment between the step and the belief push (steady refinement).
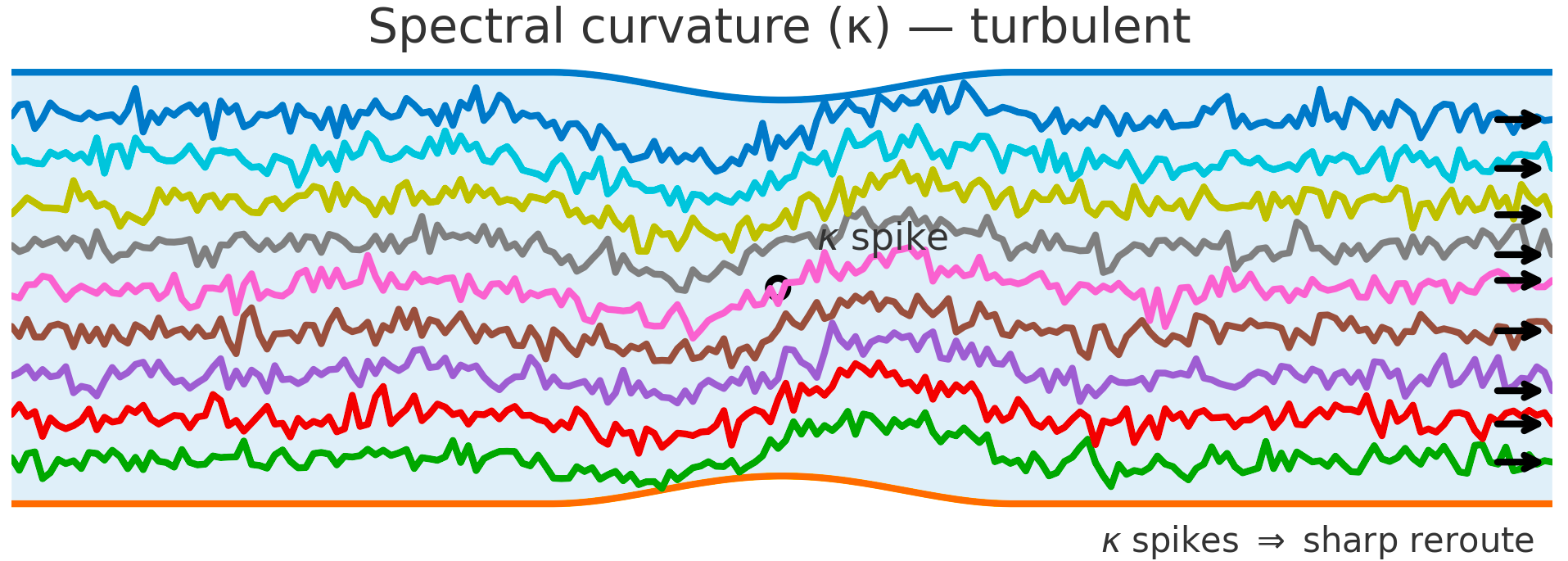
Spectral curvature ($\kappa$) — turbulent. Fluid: a bend induces sharp turning, higher shear, possible separation.
LLM Semantic Flow: a localized $\kappa$ spike at the turning point marks a sharp reroute in representation space; quasi–linear segments before/after indicate a discrete semantic pivot (e.g., topic jump, shortcut, policy jolt).
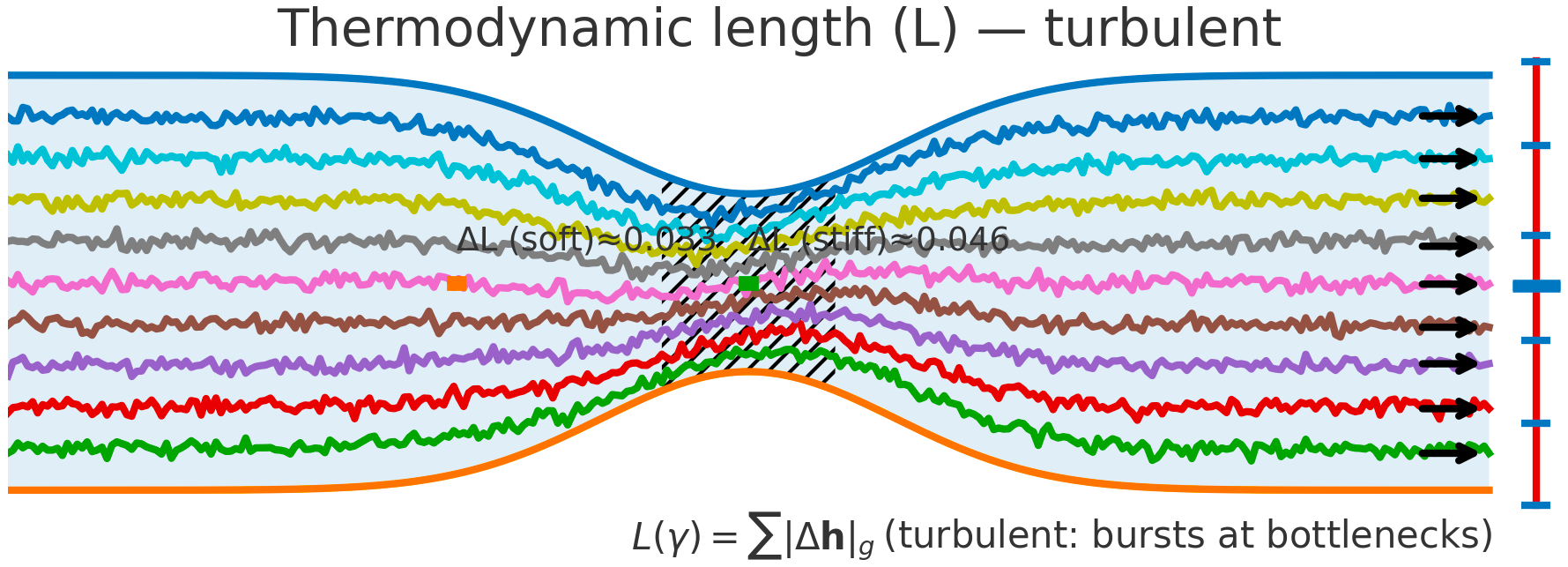
Thermodynamic length ($L$). Fluid: a constriction raises shear and pressure drop; energy dissipates fastest in the throat.
LLM Semantic Flow: a stiffer metric band (hatched) and a rise in $\Delta L$ reveal a bottleneck where extra semantic effort is paid to reshape belief (friction, detours, boundary crossing).
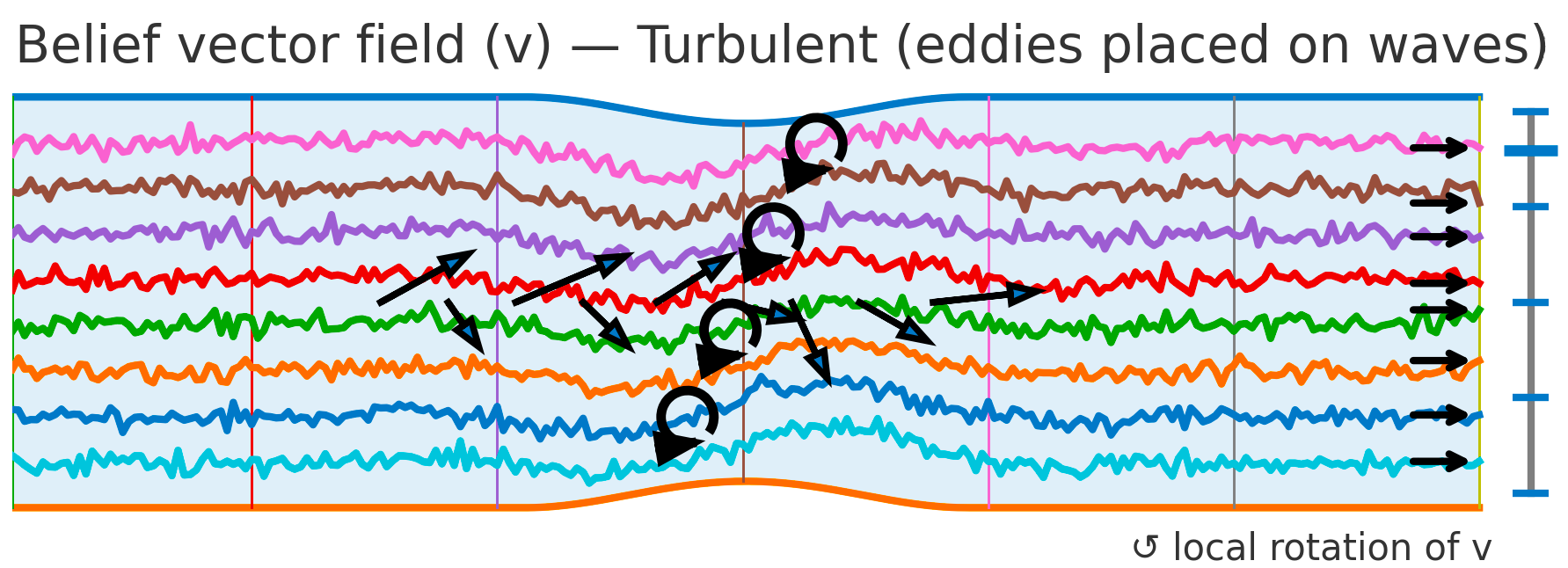
Belief field ($\mathbf{v}$). Fluid: the velocity field sets transport; eddies (local curl) mark recirculation; alignment with streamlines indicates efficient conveyance.
LLM Semantic Flow: $\mathbf{v}$ is the local push that most steeply changes the output law; longer arrows $\Rightarrow$ larger $|\mathbf{v}|$, and the side gauge shows $\cos\theta$ between $\mathbf{v}$ and the path tangent $\mathbf{T}$; circular loops on waves depict local recirculation that can trap or reinforce beliefs.
LLM as an input$\to$output semantic channel. Model: we read the forward pass as semantic hydrodynamics—a prompt injects semantic mass that is transported through depth like a fluid through a shaped conduit. Bend (top row): curvature $\kappa$ distinguishes laminar refinement from sharp reroutes. Pay (bottom left): thermodynamic length $L$ localizes where effort concentrates via $\Delta L$ bursts (bottlenecks). Push (bottom right): the belief field $\mathbf{v}$ reveals whether a layer update directly advances belief (high alignment) or reorganizes information (low alignment); eddies signal local recirculation.
Why this lens: weight–space and attention views are non–identifiable and unstable across checkpoints; nDNA instead reads the on–input trajectory and its information geometry, yielding coordinate–free, behavior–first measurements.
Vision: treat inner computation as a measurable flow so that bends, effort, and push become quantifiable traits of cognition—comparable across inputs, layers, models, and training phases.
Benefits: actionable diagnostics—$\kappa$ spikes flag brittle turns, $\Delta L$ bursts expose capacity bottlenecks, low $\cos\theta$ (between $\mathbf{v}$ and the tangent $\mathbf{T}$) indicates movement that does not immediately update belief; stable comparability—geometry–based fingerprints are robust to neuron permutations and head–role drift; governance hooks—set thresholds on $\kappa$ or $\Delta L$, track fingerprint drift after fine–tuning/pruning, and audit capacity before release.
Spectral Curvature \((\kappa_\ell)\): A Geometric Lens on Latent Bending
What is spectral curvature? In classical geometry, curvature quantifies how much a path deviates from being straight–measuring local bending of a trajectory. In spectral geometry and harmonic analysis, curvature extends to how signals or paths behave in frequency space or under operators that encode structure (e.g., Laplacians, difference operators). Spectral curvature refers to curvature derived through such operators–capturing the shape of latent signals as they evolve across layers of a model.
Why spectral for latent manifolds? In foundation models, hidden representations form a sequence of activations \(\{h_\ell\}_{\ell=0}^L\) across layers. These representations trace a path in high-dimensional latent space. The shape of this path encodes the model’s internal conceptual flow–how its beliefs evolve as it integrates priors, inputs, and alignment constraints. Spectral operators (such as discrete Laplacians or difference operators) naturally quantify how this path bends or accelerates–making them ideal for probing internal geometry. Unlike mere distance measures, spectral curvature reflects intrinsic shape, invariant under reparameterization.
Formulation and derivation. Consider hidden activations \(h_\ell \in \mathbb{R}^d\) at each layer \(\ell\). The first-order difference
\[\Delta h_\ell := h_\ell - h_{\ell-1}\]approximates the local directional change of latent states–a discrete analogue of velocity in latent space.
To capture bending, we compute the change in this directional flow–the second-order difference:
\[\Delta^2 h_\ell := \Delta h_{\ell+1} - \Delta h_\ell = (h_{\ell+1} - h_\ell) - (h_\ell - h_{\ell-1}) = h_{\ell+1} - 2h_\ell + h_{\ell-1}\]This operator acts like a discrete Laplacian along the latent path, highlighting where the model’s internal belief flow deviates from a straight trajectory.
Spectral curvature at layer \(\ell\) is defined as:
\[\kappa_\ell := \lVert\Delta^2 h_\ell\rVert = \lVert h_{\ell+1} - 2h_\ell + h_{\ell-1}\rVert\]
In continuous form, this corresponds to:
\[\kappa(s) = \left\lVert\frac{d^2 h(s)}{ds^2}\right\rVert\]where \(s\) parameterizes depth through the network. Our discrete \(\kappa_\ell\) provides a practical, layerwise estimator.
Why is this meaningful? Peaks in \(\kappa_\ell\) mark layers where internal geometry is most dynamic–zones of semantic inflection, belief compression, or ideological absorption. These are the structural signatures of internal epistemic adaptation, essential to trace cultural inheritance and alignment drift.
Lineage and context. Spectral curvature builds on tools from geometric deep learning, equivariant architectures, Ricci flow in machine learning, and spectral graph analysis [39, 40, 41, 42, 43, 44, 45, 46, 47, 48]. Within nDNA, it serves as a principled geometric fingerprint–revealing not only what is encoded, but how internal belief pathways are reshaped to encode it.
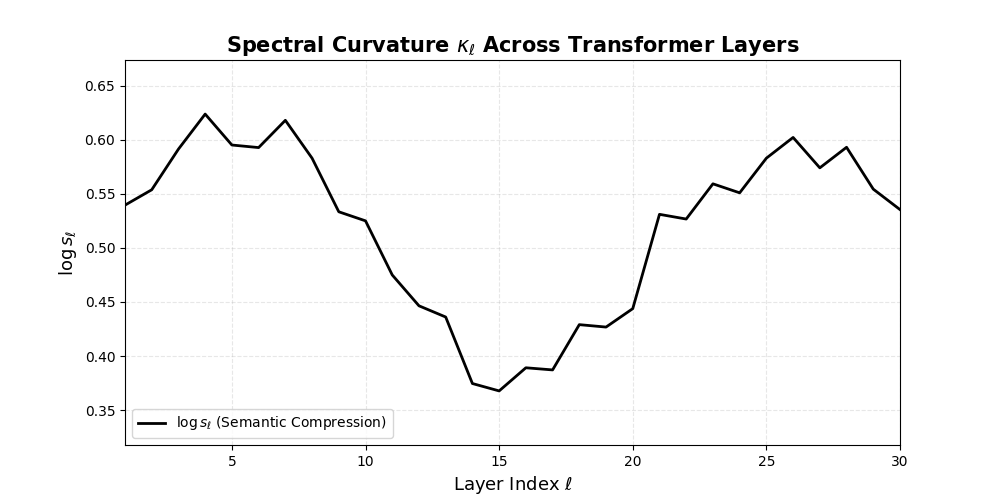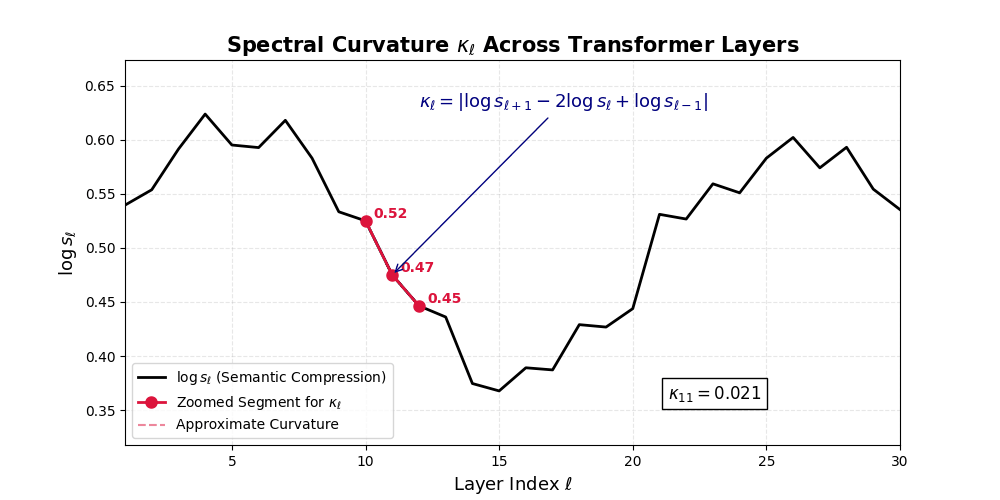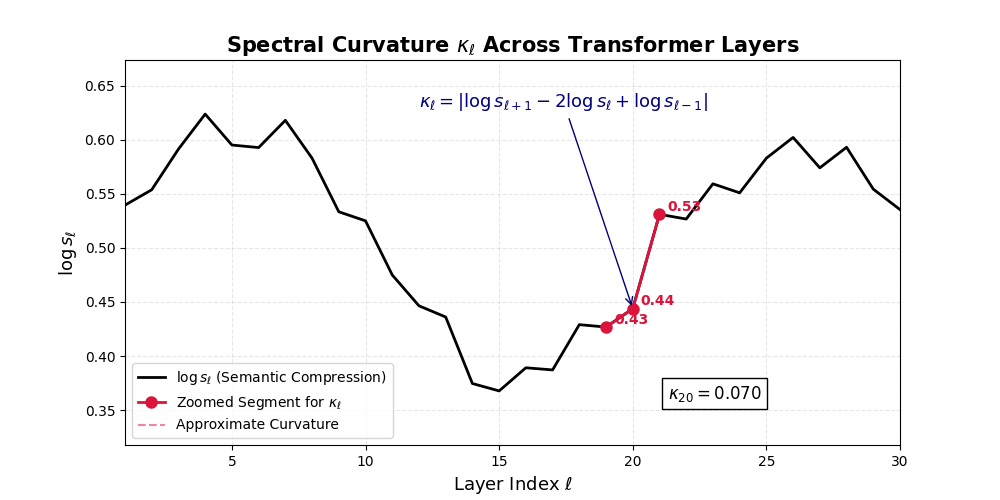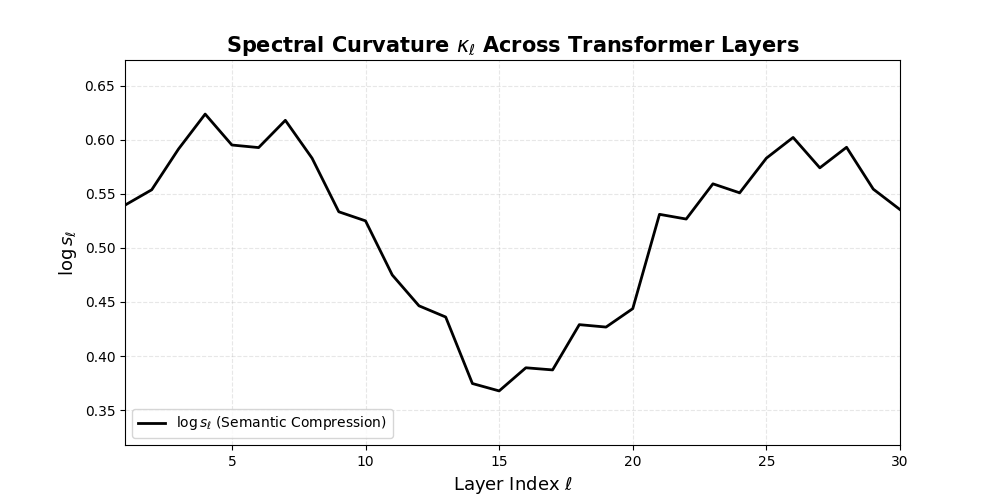
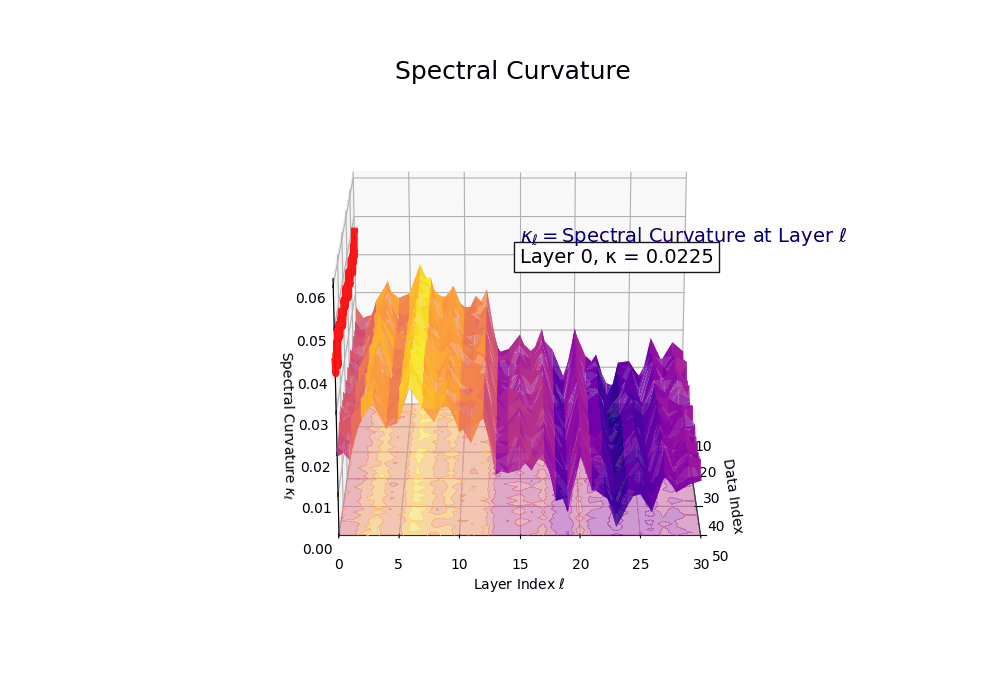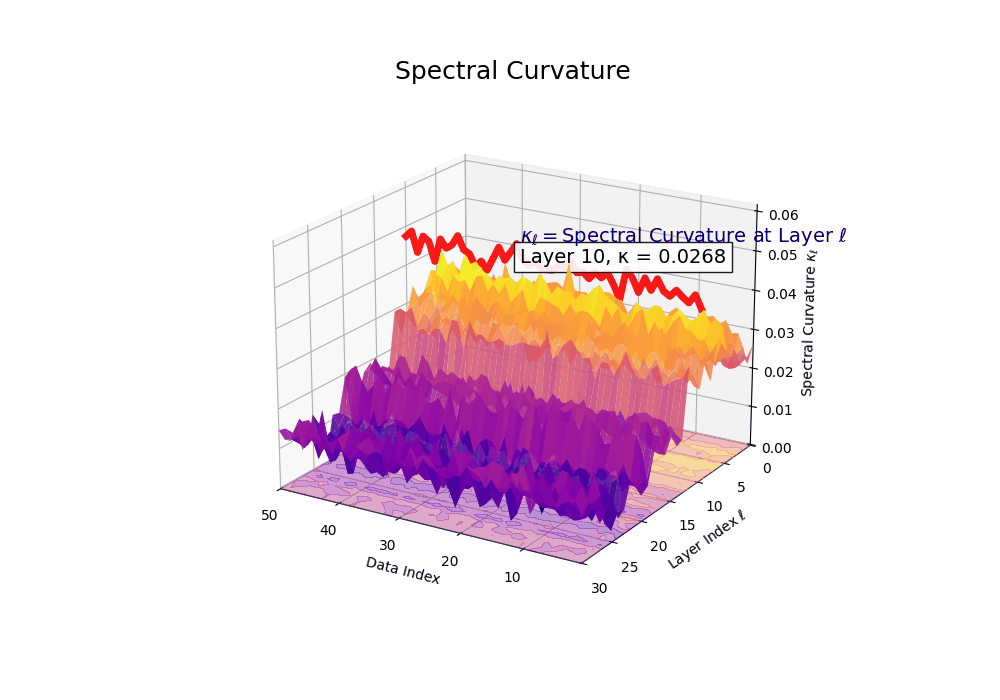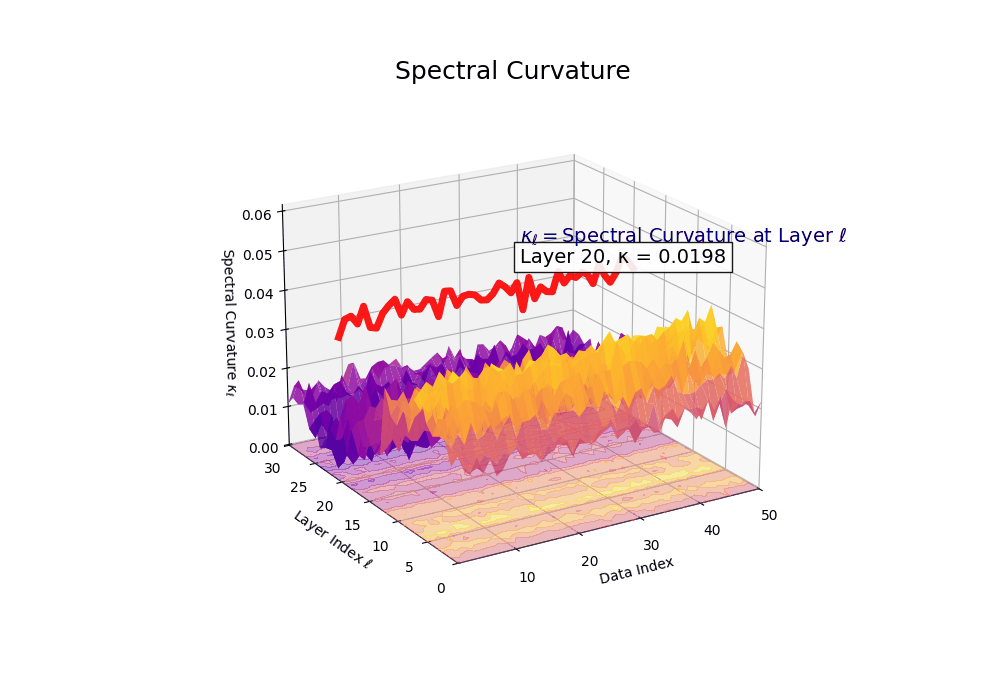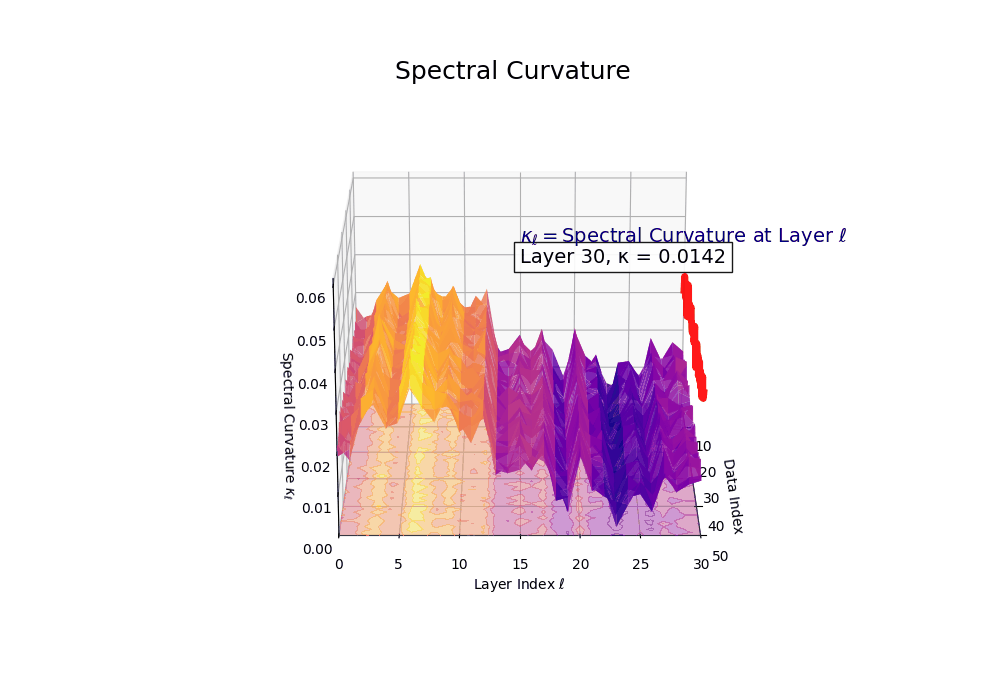
Spectral Curvature \((\kappa_\ell)\) quantifies second-order deviations in latent representations across transformer layers–computed via the discrete geometric operator \(\kappa_\ell := \lVert h_{\ell+1} - 2h_\ell + h_{\ell-1}\rVert\). High curvature signals semantic inflection points where internal geometry bends sharply–often in culturally dense, ideologically loaded, or epistemically volatile regions. Peaks in \(\kappa_\ell\) typically emerge in upper decoder layers \((\ell \in [21,30])\), where the model accommodates sociolinguistic priors during alignment, multicultural or multilingual fusion. Within the nDNA framework, such curvature reflects latent inheritance dynamics, offering a fine-grained geometric fingerprint of representational restructuring.
Thermodynamic Length \((\mathcal{L}_\ell)\): Epistemic Effort Across Layers
What is thermodynamic length? In statistical thermodynamics and information geometry, thermodynamic length measures the cumulative effort–or “work”–required for a system to transition between states on a statistical manifold. It integrates local gradient energy along a trajectory, providing an intrinsic cost measure that is independent of parametrization.
Why thermodynamic length for foundation models? In foundation models, layers trace a path through latent belief space. As input data and alignment priors reshape activations, the model expends internal computational effort to adjust its belief state. Thermodynamic length quantifies this latent effort – measuring not just what the model knows, but how hard it works to adapt that knowledge across layers in response to epistemic pressures (e.g., cultural fusion, alignment shifts).
Mathematical intuition. Let \(h_\ell\) denote the latent state at layer \(\ell\), and \(\mathcal{M}\) the model’s latent manifold. Layer transitions define a curve \(\gamma: [0,L] \to \mathcal{M}\) whose thermodynamic length is
\[\mathcal{L}(\gamma) = \int_0^L \sqrt{\langle \dot{\gamma}(s), \mathcal{G}_{\text{Fisher}} \dot{\gamma}(s) \rangle} \, ds\]
where \(\mathcal{G}_{\text{Fisher}}\) is the Fisher information metric. Here, \(\mathcal{L}(\gamma)\) represents the intrinsic work needed to traverse \(\gamma\) on \(\mathcal{M}\).
Interpretation. High thermodynamic length indicates regions where latent geometry stretches – where the model’s belief space undergoes substantial reconfiguration to reconcile priors and input. This formalism reveals not just where latent states change, but the cost structure of that change. Zones of large \(\mathcal{L}_\ell\) mark points of alignment tension, cultural fusion, or complex reasoning, where internal scaffolds are under maximum stress.
Thermodynamic length offers a window onto the model’s “latent energy budget” – illuminating how internal belief states reshape to meet complexity, constraint, and context.
Mathematical Definition
Let \(p_\ell(y\mid x)\) denote the model’s conditional distribution at layer \(\ell\) given input \(\)x. The local epistemic cost is reflected in the squared norm of the gradient of log-likelihood with respect to model parameters:
\[\lVert\nabla_\theta \log p_\ell(x)\rVert^2\]This quantity measures how much the model must adjust its parameters locally at layer \(\ell\) to improve its fit to input \(\)x. Thermodynamic length at layer \(\ell\) aggregates this cost across the dataset \(\mathcal{D}\):
Thermodynamic length at layer \(\ell\) is defined as:
\[\mathcal{L}_\ell := \sum_{x \in \mathcal{D}} \lVert\nabla_\theta \log p_\ell(x)\rVert^2 = \lvert\mathcal{D}\rvert \cdot \mathbb{E}_{x \sim \mathcal{D}} \lVert\nabla_\theta \log p_\ell(x)\rVert^2\]
This formulation reveals that \(\mathcal{L}_\ell\) captures both the average local effort and its scaling with dataset size. Furthermore, in differential geometric terms, thermodynamic length can be written as a path energy:
\[\mathcal{L}_\ell = \int_{\gamma_\ell} \left\langle \frac{dh_\ell}{ds}, \mathcal{G}_{\text{Fisher}}(h_\ell) \frac{dh_\ell}{ds} \right\rangle ds\]where \(h_\ell\) denotes latent trajectories at layer \(\ell\), \(\mathcal{G}_{\text{Fisher}}\) the Fisher information metric, and \(s\) arc length along \(\gamma_\ell\). Thus, \(\mathcal{L}_\ell\) can be seen as an energy integral over the belief manifold – capturing how much internal “heat” or computational work is generated to reconcile prior belief state with new input at depth \(\ell\).
Why is this meaningful? Unlike static capacity metrics or weight magnitudes, \(\mathcal{L}_\ell\) is dynamically grounded: it measures where the model actively strains to reconcile competing epistemic demands. In regions of high \(\mathcal{L}_\ell\), the model’s latent geometry is under tension–reshaping itself to accommodate alignment constraints, cultural priors, or multilingual semantics.
Lineage and context. This diagnostic builds on the Fisher–Rao metric in information geometry and thermodynamic length formalism from statistical physics [49, 50, 39, 51]. Thus nDNA provides a complementary view to spectral curvature–capturing not where the model bends, but how hard it works to do so. Together, these axes form a neurogeometric anatomy of latent belief adaptation.
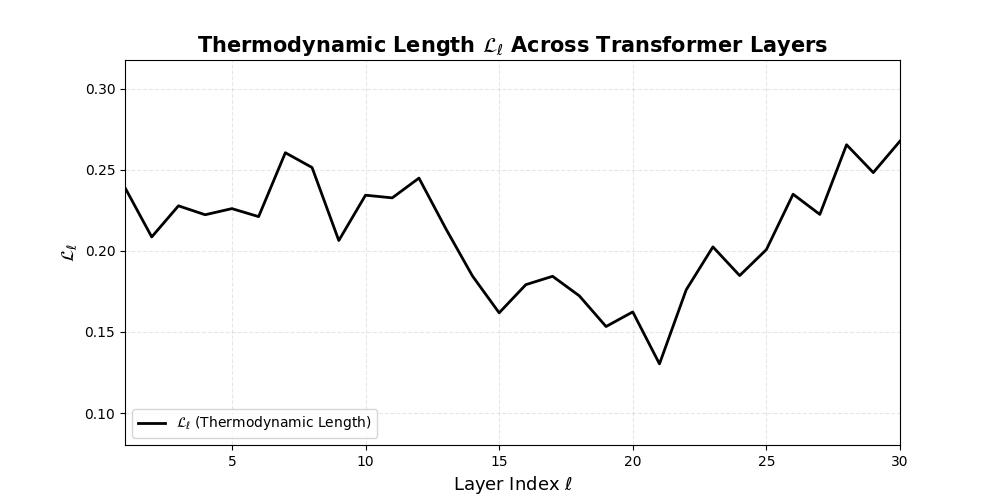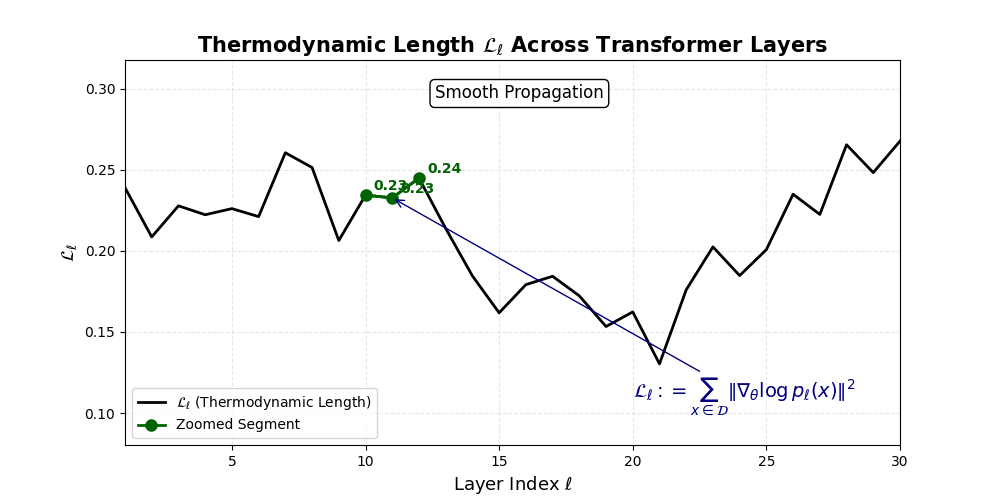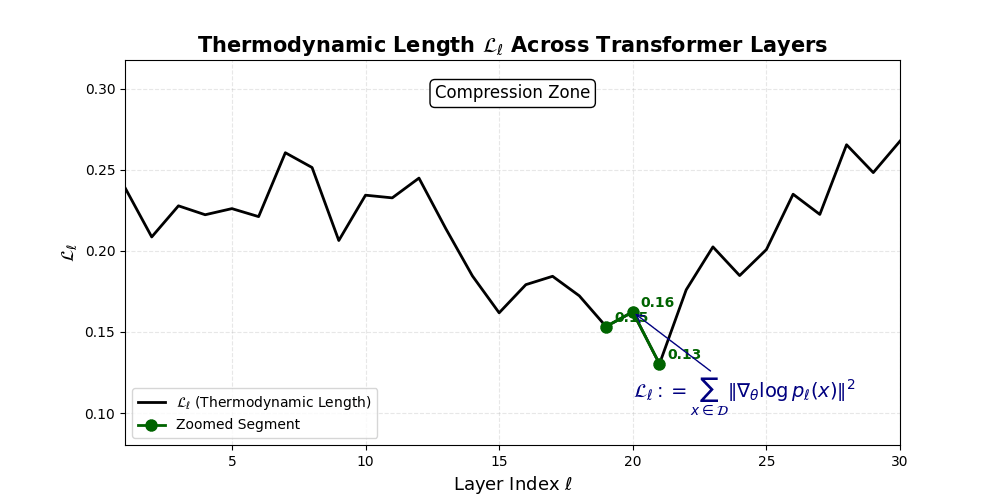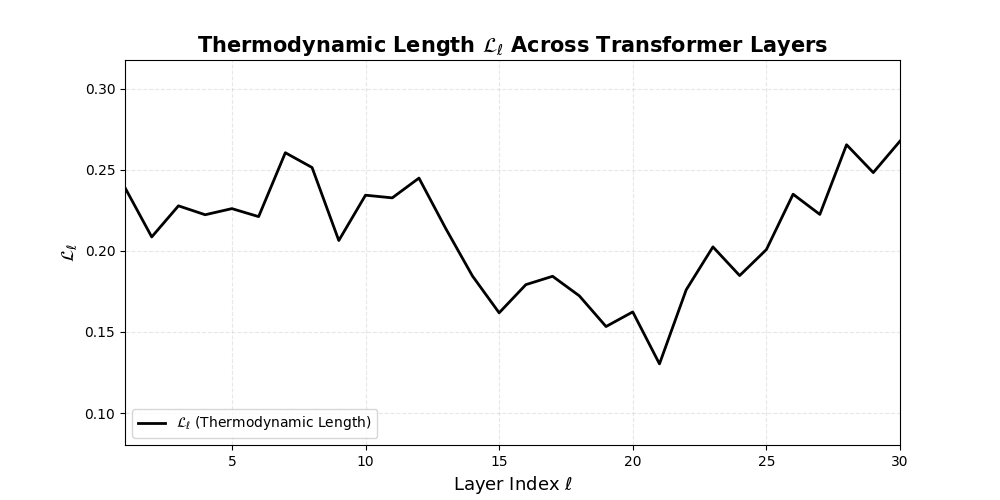
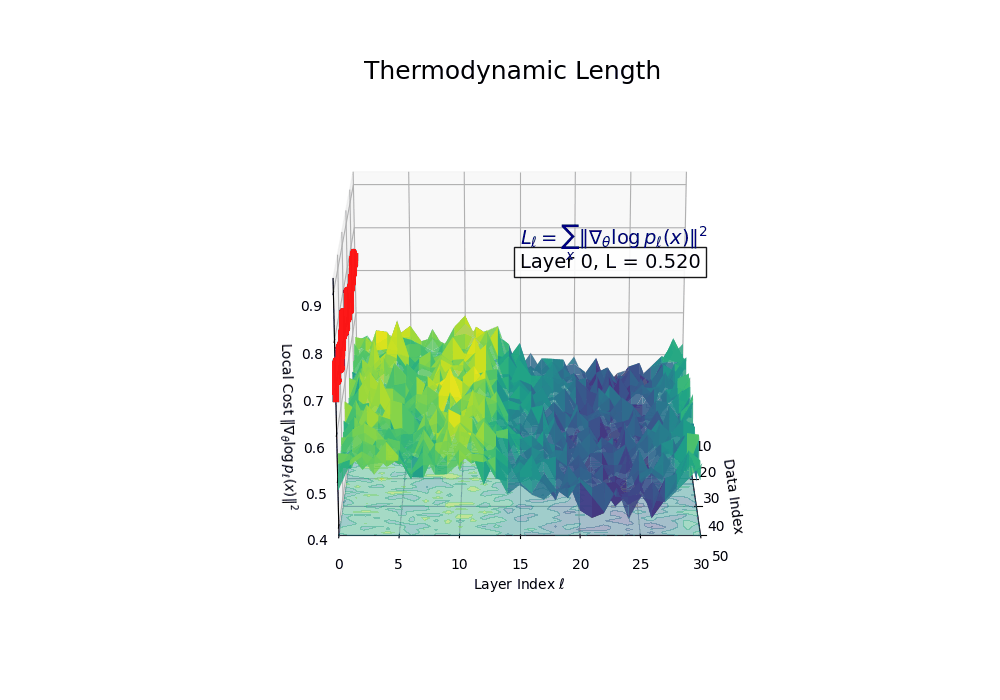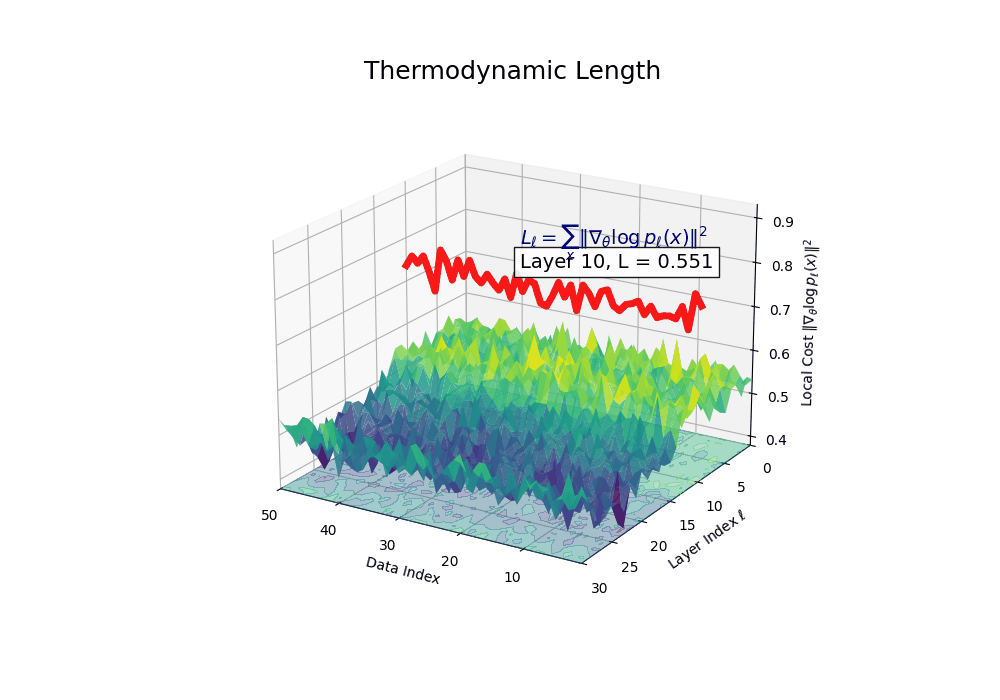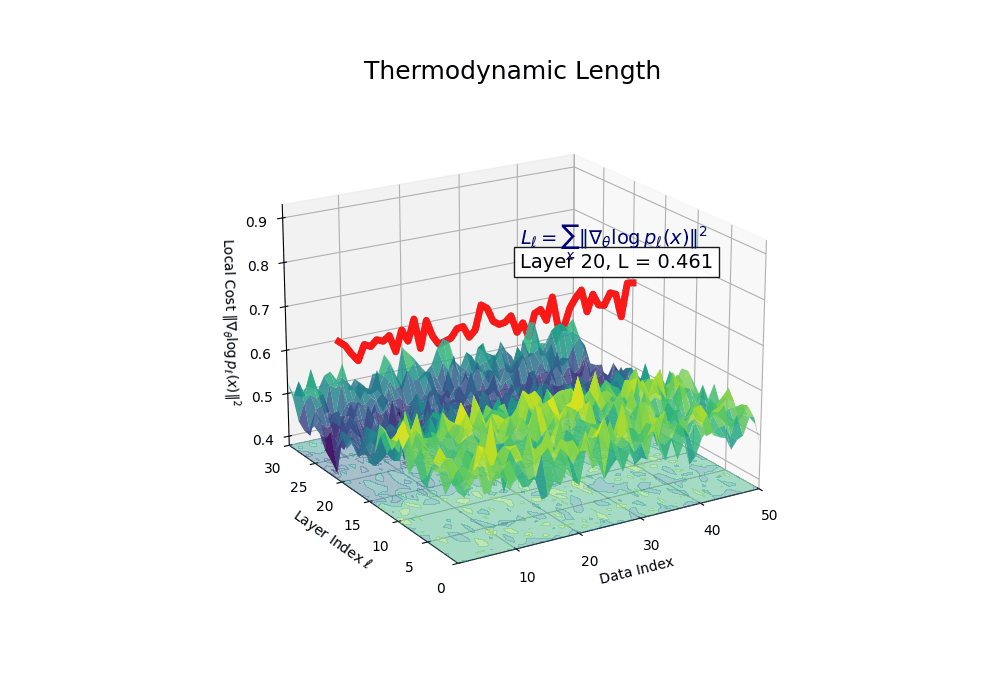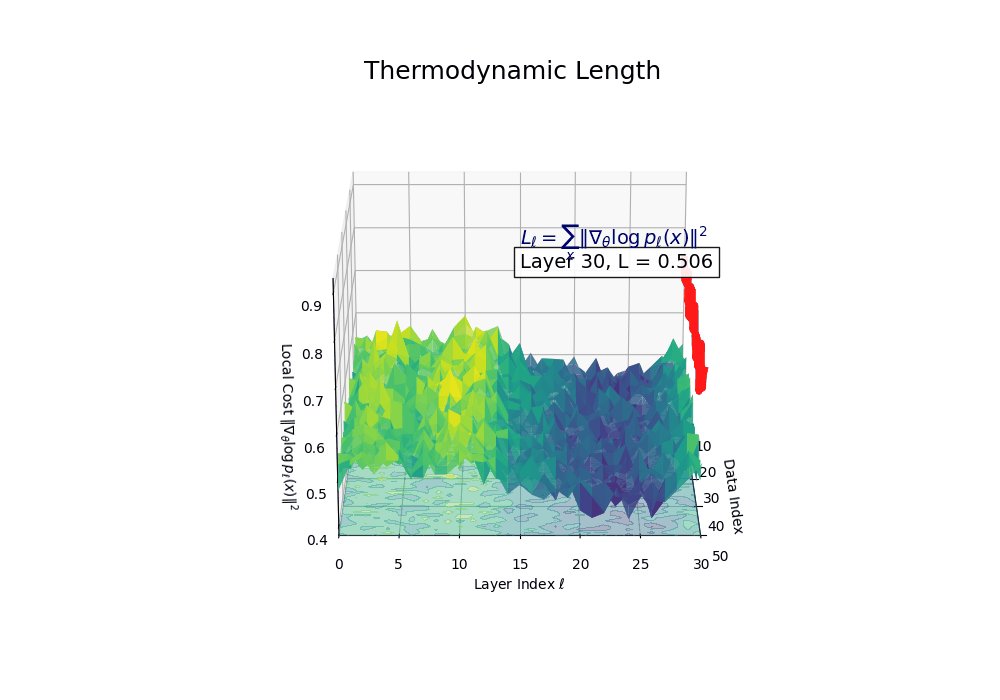
Thermodynamic Length \(\mathcal{L}_\ell := \sum_{x \in \mathcal{D}} \lVert\nabla_\theta \log p_\ell(x)\rVert^2\) quantifies the epistemic work performed across transformer layers, calculated as the cumulative squared gradient norm of layerwise log-likelihoods. Higher values signal internal resistance–zones of significant restructuring, belief compression, or negotiation of conflicting priors. In culturally fine-tuned models, these peaks localize to upper decoder layers, indicating intense adaptation near output-generating blocks. Within the nDNA construct, \(\mathcal{L}_\ell\) helps reveal latent epistemic effort that underlies surface-level behavior. This metric thus provides a nuanced window into where and how models internally allocate effort during learning and inference.
Belief Vector Field \((\mathbf{v}_\ell^{(c)})\): Cultural Drift in Latent Space
What is the Belief Vector Field– In differential geometry and physics, a vector field describes a directional force applied at each point of a space. Inspired by this, the Belief Vector Field models the directional semantic force that a specific culture or value system exerts on a model’s latent representations. It encodes where, how strongly, and in what direction cultural priors act within the model’s internal geometry–functioning as a semantic compass through the latent manifold.
Why a vector field for cultural influence? While spectral curvature \((\kappa_\ell)\) captures how sharply latent paths bend, and thermodynamic length \((\mathcal{L}_\ell)\) how hard the model works during adaptation, neither tells us the source, direction, or origin of that adaptation. The Belief Vector Field offers this missing piece: it traces the latent steering applied by culture-conditioned priors–where the model is being pushed in latent space, by what epistemic force, and toward which semantic direction. This makes it a critical diagnostic for studying cultural drift, ideological imprinting, and alignment tension.
Mathematical Definition
Let \(p(y\mid x)\) denote the model’s conditional output distribution for input \(\)x, and let \(h_\ell\) be the latent representation at layer \(\ell\). The local belief gradient, \(\nabla_{h_\ell} \log p(y\mid x)\), measures how a small change in \(h_\ell\) would affect output confidence–a proxy for semantic force at that layer. To extract the culturally conditioned semantic force, we compute its expectation over a culture-specific distribution \(\mathcal{P}^{(c)}\):
Belief vector field at layer \(\ell\) for a given manifold condition is defined as:
\[\mathbf{v}_\ell^{(c)} := \mathbb{E}_{x \sim \mathcal{P}^{(c)}} [\nabla_{h_\ell} \log p(y\mid x)]\]
where \(\mathcal{P}^{(c)}\) represents inputs emblematic of given manifold condition \(c\) (e.g., regional, linguistic, ideological contexts). This formulation captures not just latent deformation, but its cause: how cultural priors exert directional influence within the belief manifold.
Why is this meaningful? \(\mathbf{v}_\ell^{(c)}\) provides a directional lens on latent dynamics. High \(\lVert\mathbf{v}_\ell^{(c)}\rVert\) signals regions where the model is actively redirected by external cultural forces–offering diagnostic power for detecting ideological drift, semantic conflict, or bias inheritance. Unlike \(\kappa_\ell\) or \(\mathcal{L}_\ell\), which capture internal geometry, \(\mathbf{v}_\ell^{(c)}\) reveals external epistemic pressure and its directional impact.
Lineage and context. This diagnostic builds upon belief geometry, alignment drift studies, and cultural bias tracing in NLP [52, 5, 53, 54, 55, 56, 57, 58, 59, 60]. Within the nDNA construct, it integrates with curvature and length to offer a holistic neurogeometric portrait–revealing how, why, and where foundation models inherit, adapt, or distort beliefs under cultural influence.
Interpretability in practice. By mapping \(\mathbf{v}_\ell^{(c)}\) across layers and cultures, we can trace cultural provenance, identify ideological pressure zones, and diagnose inheritance asymmetry in multilingual or aligned models. This directional fingerprint informs audits of model bias, robustness, and alignment integrity–providing the missing vectorial dimension in understanding machine cognition.
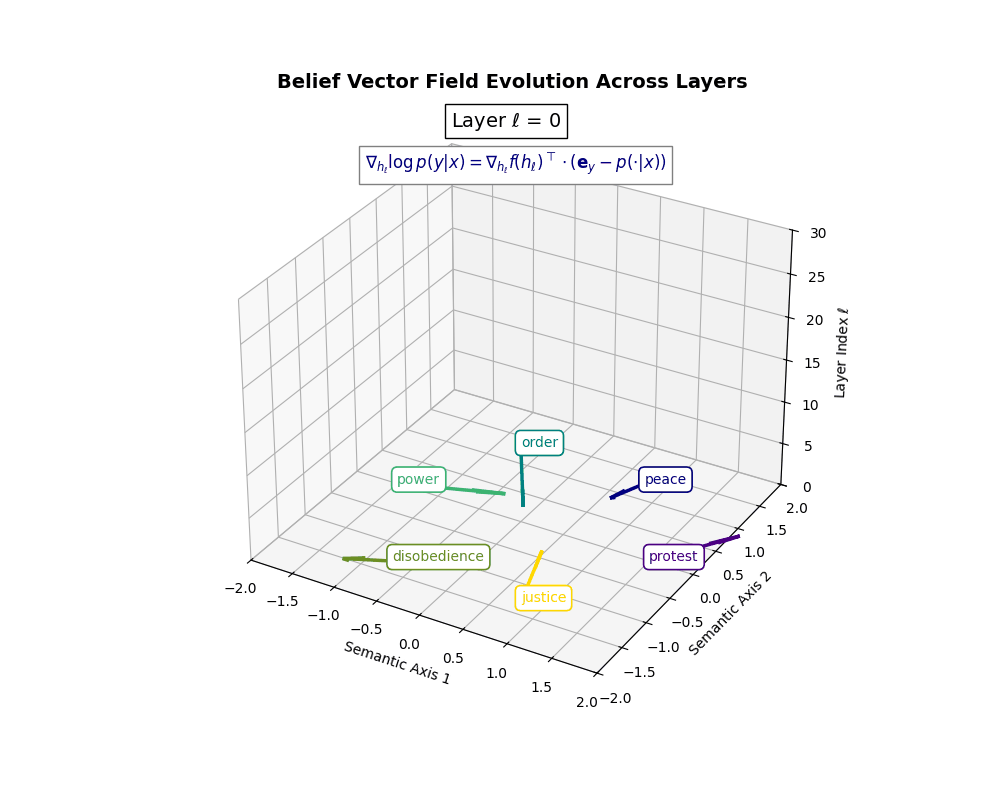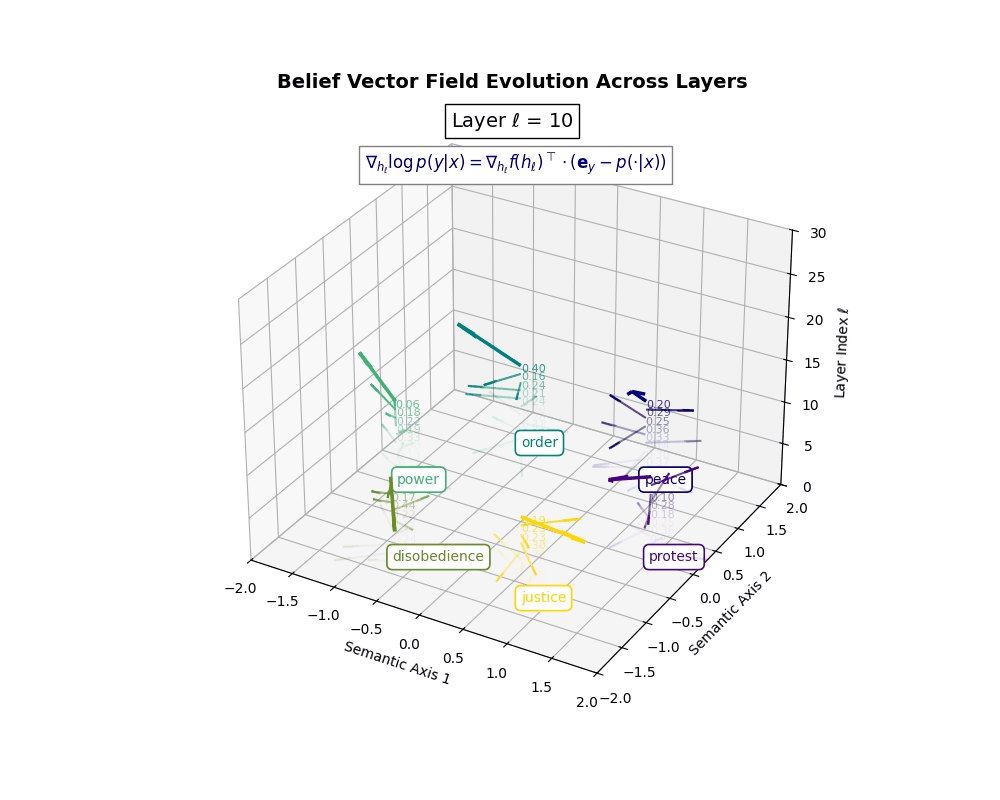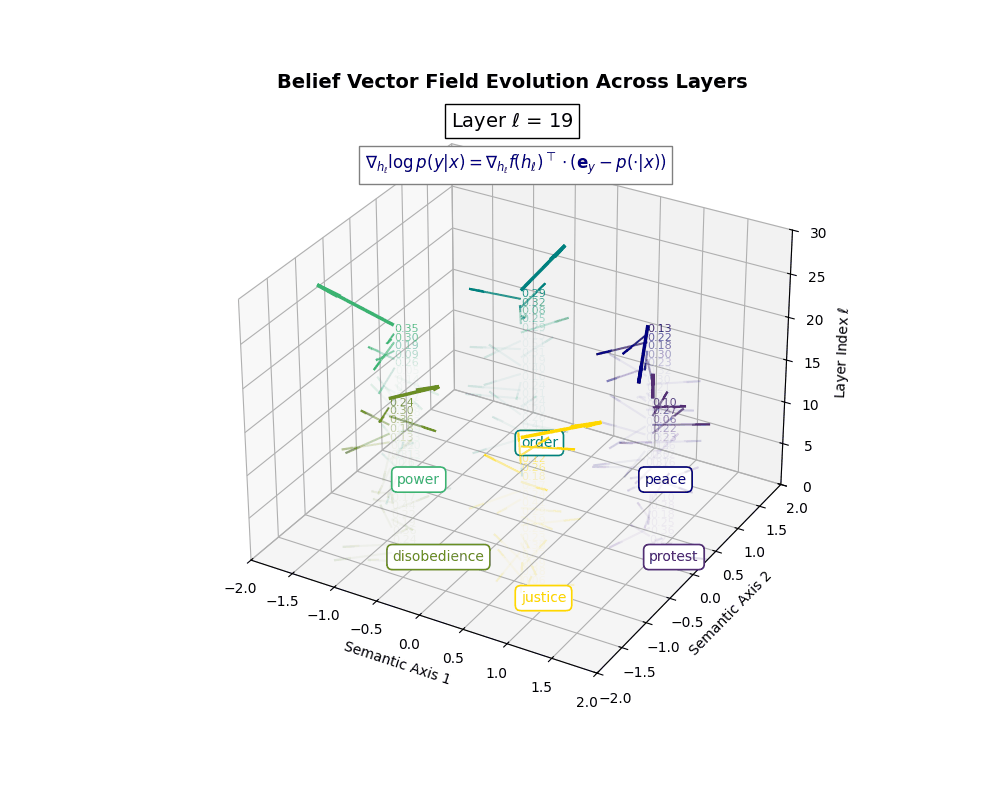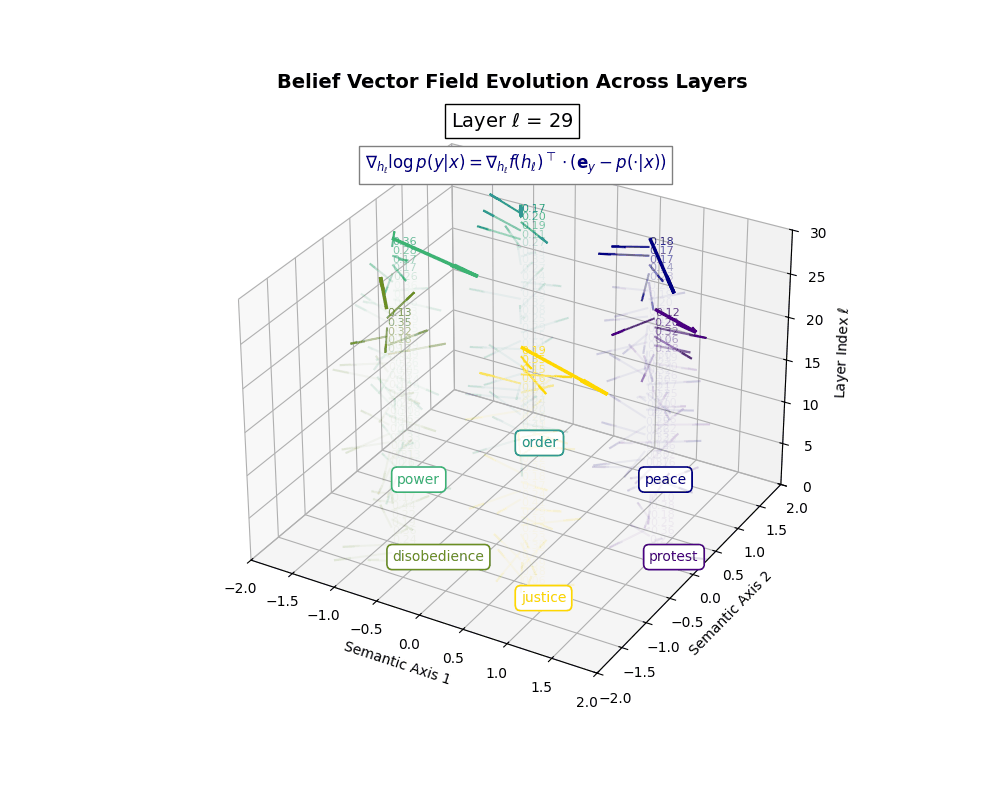
Belief Vector Field Visualization: \(\mathbf{v}_\ell^{(c)} = \mathbb{E}_{x \sim \mathcal{P}_{\text{CIVIC}}^{(c)}} [\nabla_{h_\ell} \log p(y\mid x)]\) represents the belief semantic steering force at layer \(\ell\) toward concept \(c\), conditioned on CIVIC cultural priors. Large magnitudes (e.g., \(\lVert\mathbf{v}_\ell^{(c)}\rVert \in [0.15, 0.50]\)) indicate strong directional pressure–zones where cultural values actively reshape latent geometry. Color-coded arrows trace distinct conceptual trajectories (protest, peace, order, power, disobedience, justice), while numeric labels quantify local steering strength. Upper layers \((\ell \geq 20)\) typically exhibit epistemic reorientation, where cultural priors most heavily influence belief encoding. Such visualizations reveal whether a model internalizes culturally contingent reasoning or merely mimics alignment at the output surface.
nDNA: Unified Epistemic Inheritance Measure
Why a unified score? While spectral curvature \((\kappa_\ell)\), thermodynamic length \((\mathcal{L}_\ell)\), and the belief vector field norm \((\lVert\mathbf{v}_\ell^{(c)}\rVert)\) each offer unique insight into latent dynamics, they operate on distinct facets of epistemic geometry:
The nDNA score is a cumulative measure of latent geometry, quantifying how a large language model adapts its internal scaffolding to a given corpus. It integrates three key components at each layer \(\ell\):
- Curvature \((\kappa_\ell)\): how twisted or bent the latent manifold is; captures how sharply internal trajectories bend – a scalar measure of latent acceleration.
- Length \((\mathcal{L}_\ell)\): how much latent work or displacement occurs as representations evolve; quantifies how hard the model works to adapt its beliefs – a scalar effort integral.
- Belief vector norm \((\lVert\mathbf{v}_\ell^{(c)}\rVert)\): how strong the model’s belief signal is for that corpus; encodes where and how strongly cultural priors steer latent space – a scalar magnitude derived from the vector field.
Formally, we define the nDNA score as:
\[\text{nDNA} := \sum_{\ell=1}^L \omega_\ell \cdot \kappa_\ell \cdot \mathcal{L}_\ell \cdot \lVert\mathbf{v}_\ell^{(c)}\rVert\]
Individually, these measures illuminate latent strain, adaptation cost, and cultural pressure. But to assess inheritance as a whole – how traits propagate through fine-tuning, merging, or distillation – we must integrate these into a single diagnostic that reflects combined latent geometry, epistemic work, and directional influence.
Designing the composite measure. Since \(\kappa_\ell\) and \(\mathcal{L}_\ell\) are scalars, and \(\lVert\mathbf{v}_\ell^{(c)}\rVert\) reduces directional drift to scalar magnitude, their product forms a natural joint measure of: internal bending \((\kappa_\ell)\), internal epistemic effort \((\mathcal{L}_\ell)\), and external drift pressure \((\lVert\mathbf{v}_\ell^{(c)}\rVert)\). To balance their contributions across depth, we introduce layer weights \(\omega_\ell\), emphasizing semantically active or epistemically significant layers (e.g., \(\omega_\ell\) higher in upper decoder blocks).
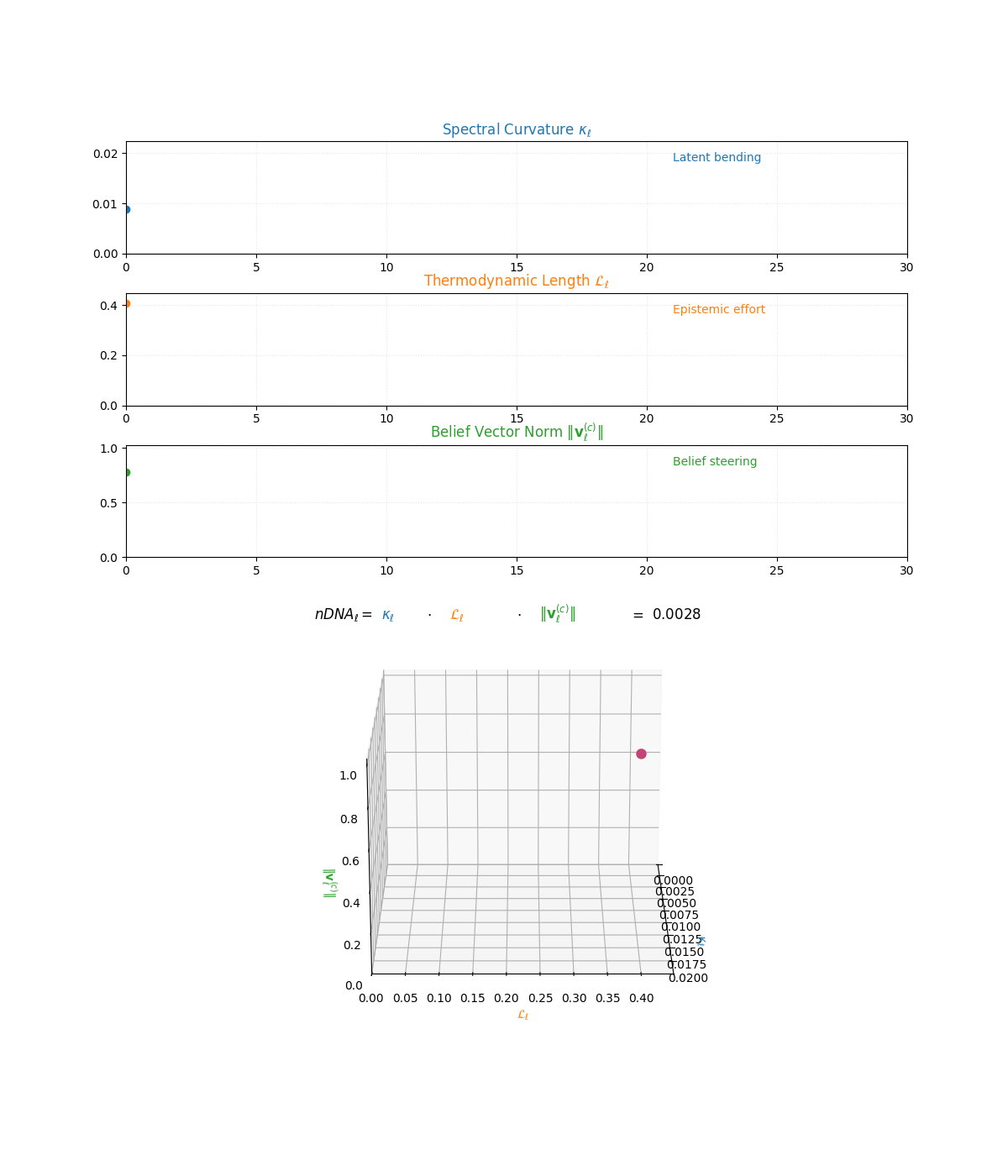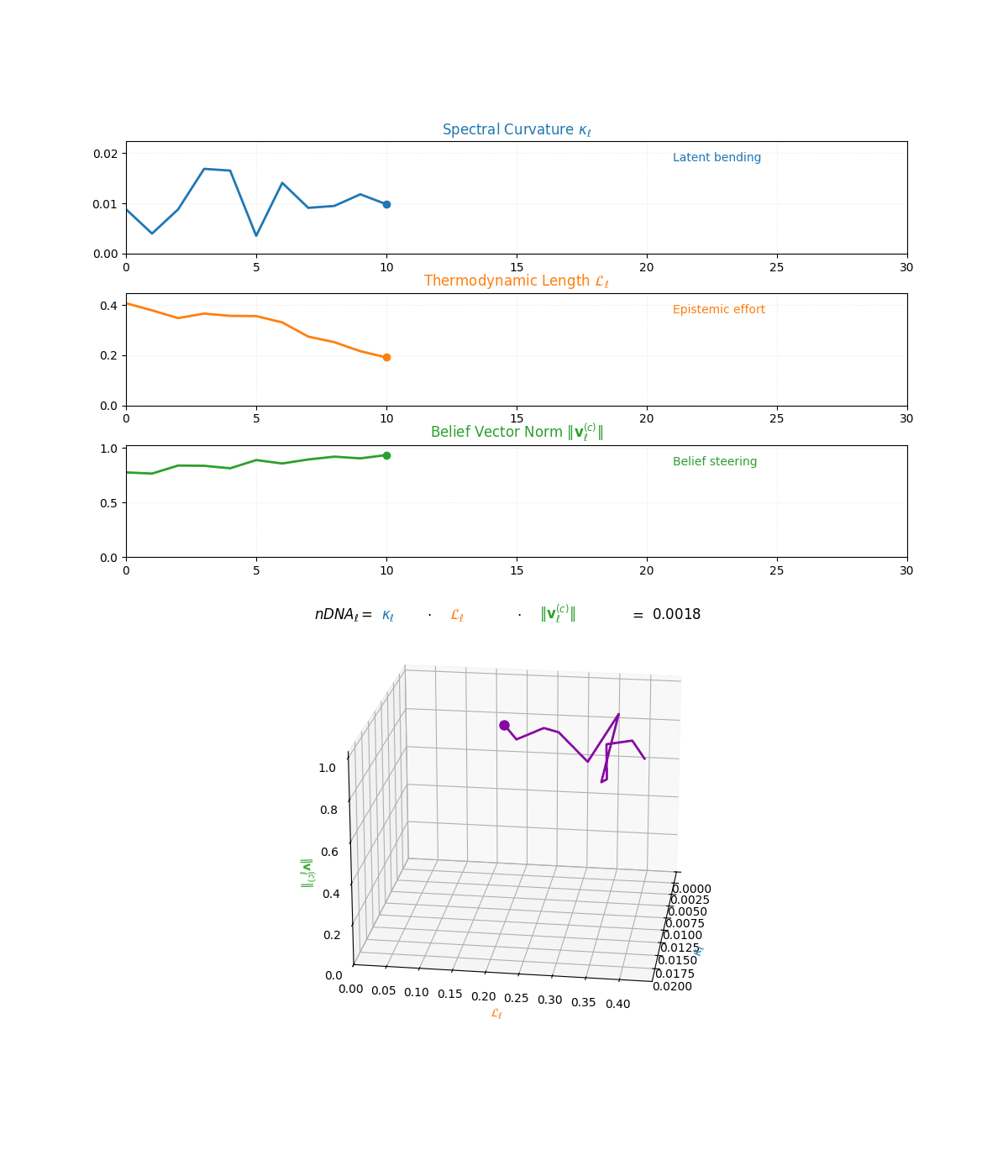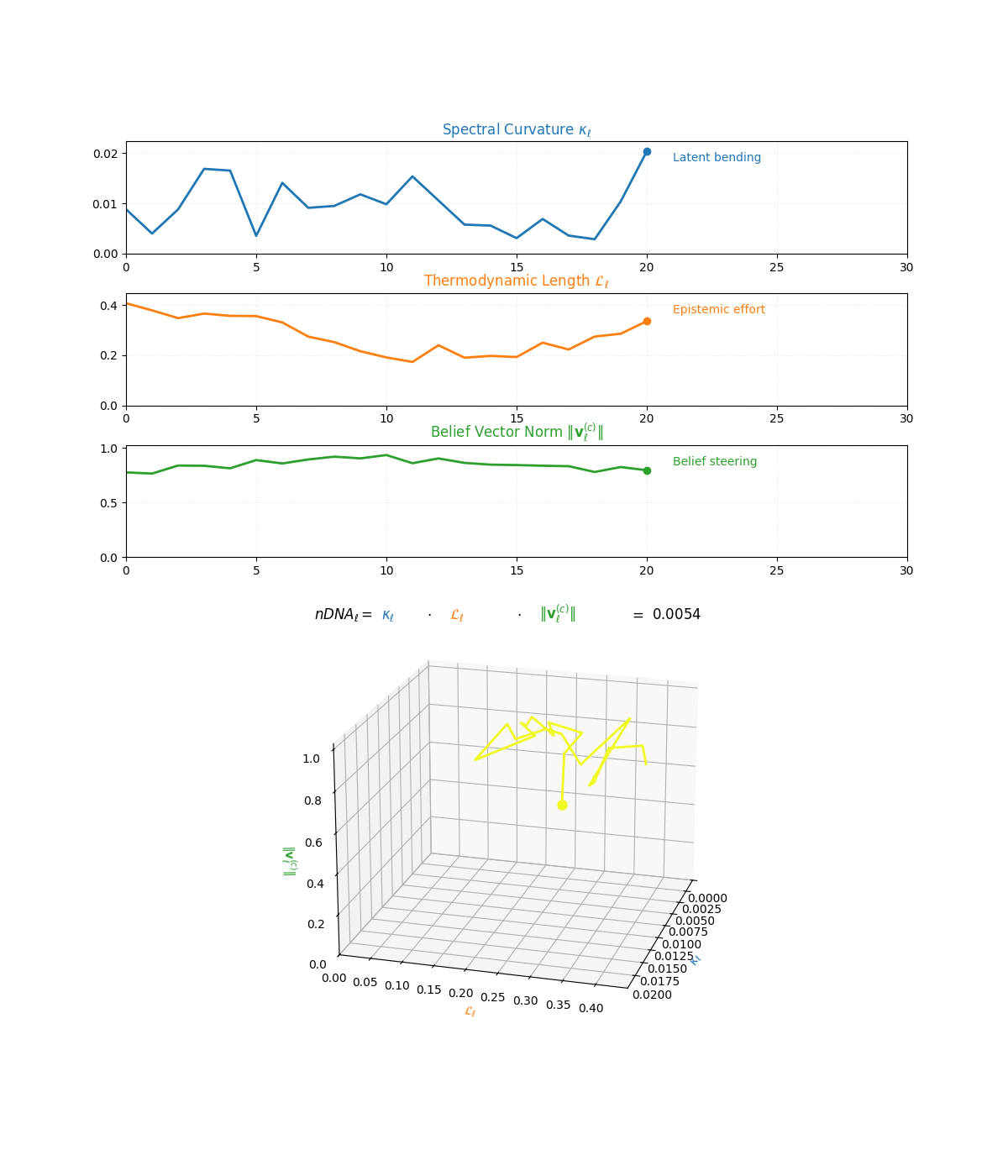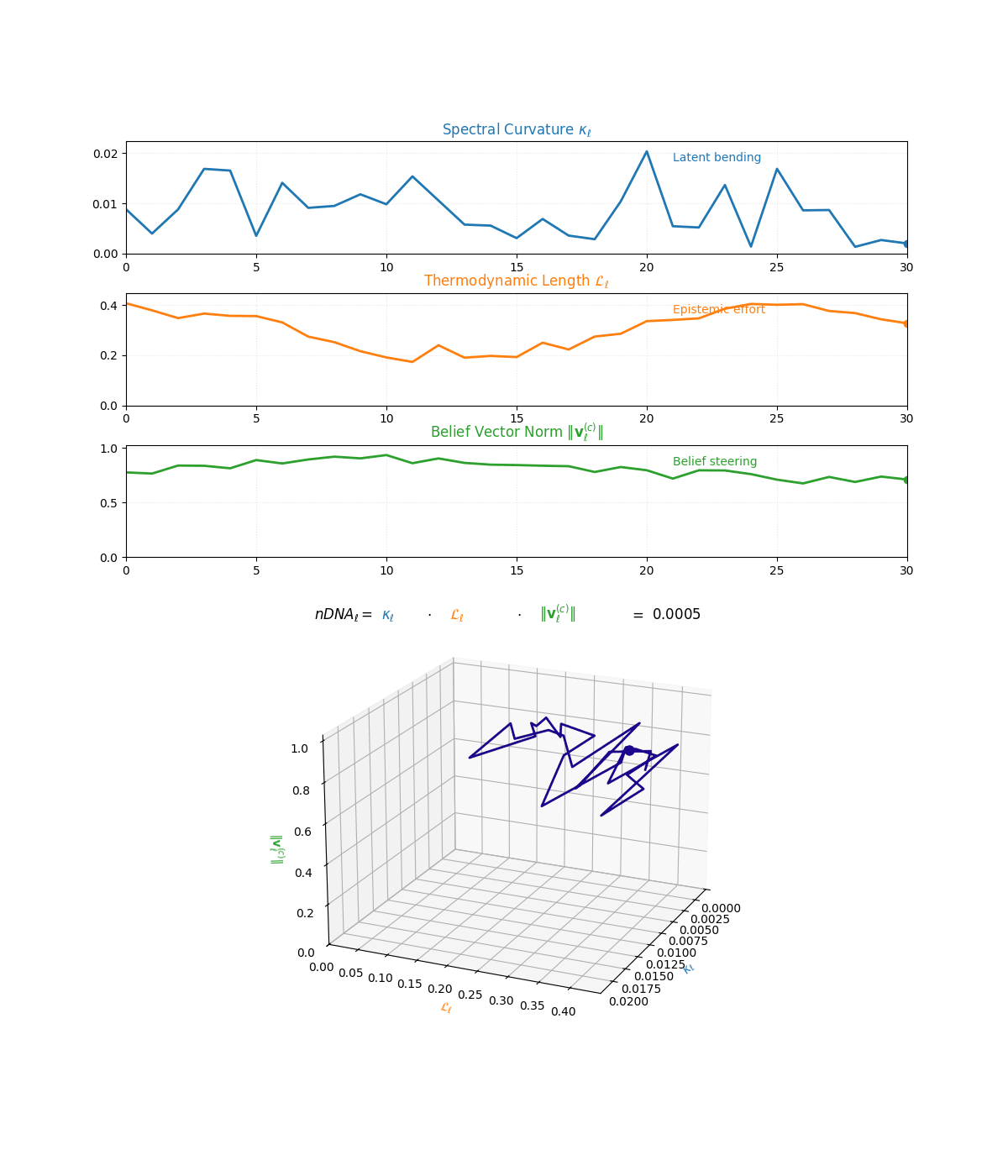
The compositional anatomy of neural DNA (nDNA) through curvature, length, and belief geometry. This figure illustrates how nDNA arises as a layered product of three latent quantities. First, spectral curvature \(\kappa_\ell\) measures latent manifold bending and flexibility (latent acceleration), indicating how sharply the internal geometry twists at layer \(\ell\). Second, thermodynamic length \(\mathcal{L}_\ell\) quantifies the accumulated epistemic effort (latent adaptation energy) and reflects how hard the model works to reconcile prior beliefs with new input and alignment signals. Third, belief vector norm \(\lVert\mathbf{v}_\ell^{(c)}\rVert\) encodes the magnitude of latent directional force imposed by corpus priors or alignment signals. The joint trajectory in \((\kappa_\ell, \mathcal{L}_\ell, \lVert\mathbf{v}_\ell^{(c)}\rVert)\) space, color-coded by the composite score, shows how bending, effort, and steering co-evolve across layers. The combined latent signature is formalized as \(\text{nDNA}_\ell = \kappa_\ell \cdot \mathcal{L}_\ell \cdot \lVert\mathbf{v}_\ell^{(c)}\rVert = 0.0024\) (example layer), with high values identifying zones of intense latent reconfiguration where geometry and adaptation forces align. Color-keyed descriptors (“Latent bending”, “Epistemic effort”, “Belief steering”) guide visual interpretation. The figure illustrates how large language models coordinate latent bending, effort, and steering to build a neurogeometric scaffold that adapts flexibly to task complexity while remaining anchored in a universal latent structure.
This composite score integrates scalar and vector-derived diagnostics into a unified measure of epistemic inheritance – quantifying the latent structure and cultural traits a model carries forward from its neural ancestry.
Rationale for multiplicative integration. This form spotlights layers where latent paths bend sharply, belief adaptation incurs significant effort, and cultural or alignment pressures apply strong directional force. High scores identify zones of intense latent reconfiguration, where internal dynamics and external pressures converge to reshape the model’s reasoning space.
Role of \(\omega_\ell\). The weight \(\omega_\ell\) serves as a lens to prioritize semantically expressive, epistemically active regions of the network. It may be set uniformly, hand-tuned, or optimized against alignment drift benchmarks, bias metrics, or interpretability objectives.
Interpretability and utility. The nDNA score provides a compact fingerprint of model inheritance:
- It enables direct comparison of parent and child models post fine-tuning, merging, or distillation.
- It highlights zones of semantic mutation, ideological absorption, or cultural drift.
- It serves as a proxy for latent epistemic integrity – quantifying the hidden cost and directionality of neural evolution.
By unifying spectral, thermodynamic, and vectorial diagnostics, the nDNA score functions as a heritable geometry index – diagnosing how latent traits persist, mutate, or degrade as foundation models evolve.
nDNA Geometry: A Closer Look
The notion of nDNA arises from a simple yet profound insight: modern foundation models do not merely produce outputs–they embody a latent cognitive structure that governs how they reason, adapt, and evolve [55, 6]. This latent structure is not directly encoded in model weights or activations alone; rather, it emerges in the internal geometry of belief formation, semantic flow, and epistemic adaptation across layers [4, 47]. We define the nDNA geometry of a model as the joint distribution of its spectral curvature (\(\kappa_\ell\)), thermodynamic length (\(\mathcal{L}_\ell\)), and belief vector field norm (\(\lVert\mathbf{v}_\ell^{(c)}\rVert\)) layer-by-layer. This triad forms a high-dimensional semantic fingerprint that encodes a model’s inheritance stability, alignment dynamics, and cultural drift—analogous to how biological DNA records heritable traits and mutations [53, 16].
| Layer | $$\kappa_\ell$$ | $$\mathcal{L}_\ell$$ | $$\lVert\mathbf{v}_\ell^{(c)}\rVert$$ | Belief Vector $$\mathbf{v}_\ell^{(c)}$$ |
|---|---|---|---|---|
| 20 | 0.0412 | 0.9123 | 0.6521 | [0.1204, -0.0502, 0.0896, …, 0.0402] |
| 21 | 0.0458 | 0.8123 | 0.7523 | [0.1301, -0.0351, 0.0950, …, 0.0431] |
| 22 | 0.0523 | 1.0120 | 0.5823 | [0.1423, -0.0312, 0.0994, …, 0.0488] |
| 23 | 0.0581 | 0.9021 | 0.6912 | [0.1534, 0.0270, 1.0042, …, 0.0512] |
| 24 | 0.0639 | 1.1023 | 0.5520 | [0.1667, 0.0205, 1.1105, …, 0.0543] |
| 25 | 0.0505 | 0.9420 | 0.8124 | [0.1602, -0.0251, 1.0081, …, 0.0504] |
| 26 | 0.0398 | 0.8520 | 0.6120 | [0.1251, 0.0450, 0.0912, …, 0.0418] |
| 27 | 0.0512 | 1.0520 | 0.7222 | [0.1455, -0.0322, 1.0005, …, 0.0477] |
| 28 | 0.0590 | 0.9320 | 0.5721 | [0.1577, 0.0285, 1.0078, …, 0.0499] |
| 29 | 0.0672 | 1.0123 | 0.6322 | [0.1701, -0.0198, 1.1142, …, 0.0533] |
| 30 | 0.0555 | 0.8221 | 0.7720 | [0.1620, -0.0242, 1.1101, …, 0.0510] |
This table provides an illustrative example of nDNA geometry, highlighting how these quantities vary across depth in a representative model. Rather than simple monotonic trends, we observe intricate layer-wise patterns: certain layers exhibit elevated curvature (\(\kappa_\ell > 0.06\)), signaling sharp latent reorientation [40], while others concentrate thermodynamic length (\(\mathcal{L}_\ell > 1.10\)), reflecting zones of intense internal work to reconcile competing priors [49, 50]. The belief vector norm \(\lVert\mathbf{v}_\ell^{(c)}\rVert\) exposes the directional cultural force acting on the latent manifold [56, 5], marking layers where external alignment or sociolinguistic conditioning exerts greatest influence. Together, these values form a geometry-specific trace that distinguishes models by their latent adaptation history.
The Corpus Dependence of nDNA: A Necessary Feature, Not a Flaw
In biological systems, DNA is celebrated as the universal code of life – a sequence of nucleotides that, across all known organisms, governs the development, function, and inheritance of traits [61, 62]. Yet despite this universal structure, the functional expression of DNA is profoundly context-dependent. The same genome, when expressed in different cellular contexts, gives rise to vastly different phenotypes: for instance, neurons and hepatocytes arise from identical genetic material yet serve radically different functions [63, 64]. This context-sensitive expression is orchestrated through layered regulatory mechanisms, including epigenetic modifications [63], transcription factor (TF) binding [65], and chromatin architecture remodeling [66, 67]. These mechanisms form a hierarchical, probabilistic regulatory network that determines gene expression patterns in response to developmental and environmental cues [68].
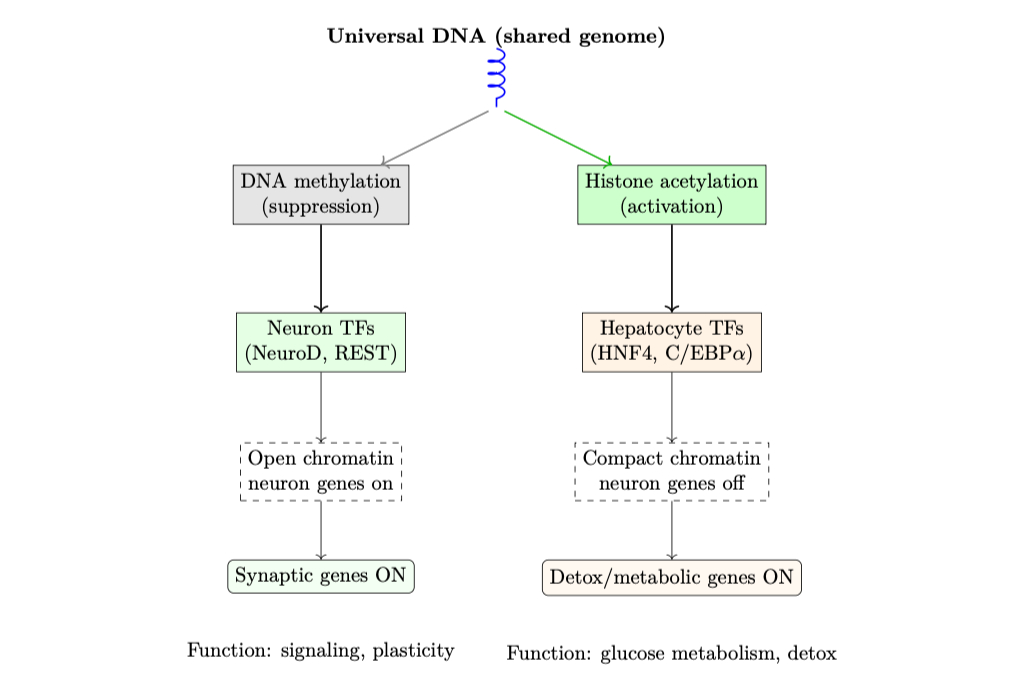
A hierarchical view of universal DNA and context-sensitive gene expression, as a biological parallel to nDNA latent scaffolding in LLMs. This figure illustrates how the same genome (depicted as a universal DNA helix at the top) produces distinct functional outcomes through a layered and structured regulatory architecture. The first regulatory layer consists of epigenetic modifications, including DNA methylation (linked with gene silencing) and histone acetylation (linked with gene activation) [63, 66]. These modifications influence chromatin accessibility, setting the stage for context-specific transcriptional control. The second layer involves cell-type-specific transcription factors (TFs) – for example, NeuroD and REST in neurons, or HNF4 and C/EBPα in hepatocytes – which bind regulatory DNA elements and integrate signaling cues to guide gene expression programs [65, 64]. The third layer reflects the resultant chromatin state: open, transcriptionally permissive configurations in neurons for synaptic gene activation, versus compact, repressive configurations in hepatocytes where those genes are silent [69, 67]. Finally, this hierarchical regulatory control produces functionally specialized gene programs: neurons activate synaptic plasticity and axon signaling genes; hepatocytes activate detoxification and glucose metabolism genes [62, 68]. This layered architecture provides a powerful biological analogy for nDNA in LLMs. Just as DNA’s expression is shaped by regulatory logic rather than random variation, nDNA encodes both universal priors (shared across tasks) – such as pretrained latent manifolds, attention mechanisms, and model architecture – and corpus-dependent latent scaffolding, emerging as the model adapts to specific tasks or domains [70, 71, 72]. The analogy emphasizes that corpus dependence in nDNA is not a weakness or artifact, but a reflection of meaningful task adaptation: structured variation grounded in universal latent geometry. This scaffolding ensures LLMs achieve functional diversity across tasks while maintaining coherence, alignment, and generalization, much like gene regulatory networks ensure appropriate cellular identity and function despite operating from a common genome blueprint [68, 64]. The figure highlights that both biological DNA and nDNA exhibit clarity through complexity: layered, interpretable hierarchies enabling flexible, robust expression across contexts.
Similarly, in large foundation models, the neural DNA (nDNA) – a composite measure of latent geometry encompassing spectral curvature \((\kappa)\) [73], thermodynamic length \((L)\) [74], and latent belief vector norms [70] – exhibits both universal structure and corpus-specific adaptation. LLMs encode universal latent priors through pretraining: architectural invariances [75], semantic manifolds [76, 77], and attention-based relational structures [71]. However, when probed with different corpora – such as mathematical reasoning benchmarks (e.g. GSM8K [78]), dialogue datasets (e.g. MultiWOZ [79]), or encyclopedic QA (e.g. SQuAD [80]) – the model activates distinct latent scaffolding, producing task-specific geometric pathways.
In both systems, structured variation emerges as a necessity: in biology, to produce functional diversity across cell types; in LLMs, to scaffold reasoning across tasks while maintaining alignment and generalization [77, 78]. Like tissue-specific gene expression, corpus-dependent nDNA scaffolding follows precise, learned priors rather than arbitrary variation. Mathematical models of both systems reduce to path integrals over conditional cost:
\[\mathcal{S}(c) = \int_{\gamma_c} \mathcal{C}(h_\ell; c) \, ds\]where \(\gamma_c\) is the pathway for context \(c\) (cell type or corpus), and \(\mathcal{C}\) reflects regulatory or loss cost.
Where DNA differentiates cells, nDNA differentiates reasoning. Both systems achieve functional coherence through context-dependent geometry anchored in universal code.
Despite their contextual variation, both DNA and nDNA encode universal structure that stabilizes functional diversity. In biology, this universality is embodied in the genetic code: the shared language of codons, conserved regulatory motifs, and chromatin architectural principles that ensure coherent development across tissues [62, 61]. In large language models, nDNA’s universality arises from the shared latent priors learned during pretraining: attention-based relational structures [75], semantic manifolds [76], and transformer-invariant latent symmetries [77]. These priors act as the “genomic grammar” that binds task-specific latent pathways into a coherent reasoning framework.
\[\boxed{\textbf{DNA: }\Sigma^3 / \ker \phi \to \mathcal{A}\quad\textbf{nDNA: }\mathcal{X} / G_{\text{LLM}} \to V/G}\]Such universal structure enables generalization: in biology, reliable organismal development; in LLMs, reasoning consistency and alignment across tasks. Crucially, this structure constrains corpus-dependent variation within interpretable latent geometry – preventing arbitrary or adversarial drift [71, 78].
What DNA is to the unity of multicellular life, nDNA is to the coherence of LLM reasoning: a stabilizing universal code that enables structured functional variation.
Evolutionary and Learning Dynamics: Convergence of Principles
Both DNA and nDNA are shaped by selection processes. In biology, the genome has evolved under millennia of selective pressure, with regulatory networks fine-tuned to ensure robust development and adaptability [68, 64]. In LLMs, pretraining operates as an evolutionary analogue: stochastic gradient descent (SGD) over massive corpora selects latent priors that minimize expected loss across tasks, with fine-tuning akin to epigenetic adjustment [77, 81].
\[\underbrace{\mathcal{L}_{\text{pretrain}}(\theta) = \mathbb{E}_{(x,y)} [-\log p_\theta(y|x)]}_{\textbf{SGD as selection pressure}}\]This evolutionary parallel explains why both systems exhibit clarity through complexity: layered hierarchies, probabilistic pathways, and interpretable modularity. Where biological evolution yields modular gene regulatory networks that ensure context-sensitive expression [68], LLM training yields modular latent structures – such as attention heads and adapter modules – that scaffold task-specific reasoning [71, 81].
Why Corpus Dependence Matters
Far from a flaw, corpus dependence in nDNA is the signature of a flexible, adaptive reasoning architecture. Just as biological systems rely on tissue-specific gene expression to produce functional diversity from a universal genome [64, 68], large language models (LLMs) leverage corpus-dependent latent scaffolding to generate reasoning structures attuned to task demands, mirroring the reproducibility logic of biological variability quantification [82]. By examining nDNA’s spectral curvature \((\kappa)\), thermodynamic length \((\mathcal{L})\), and belief vector norm \((\lVert\mathbf{v}_\ell^{(c)}\rVert)\), we gain a diagnostic lens for alignment, generalization, and safety [73, 74, 70]:
\[\mathcal{S}_{\text{nDNA}}(c) = \int_{\gamma_c} \left(\alpha\kappa + \beta\mathcal{L} + \gamma\lVert\mathbf{v}_\ell^{(c)}\rVert\right) \, ds\]where \(\gamma_c\) is the latent trajectory for corpus \(c\). This latent geometry echoes Waddington’s epigenetic landscape where paths represent developmental fates [83].
QA tasks evoke compact low-curvature paths (e.g. \(\kappa \sim 0.012\)–\(0.03\), \(\mathcal{L} \sim 0.47\)–\(0.53\)) [80, 84, 85], while reasoning tasks elicit broader high-curvature paths (e.g. \(\kappa \sim 0.005\)–\(0.04\)) [78, 86, 71]. Dialogue corpora produce shallow clustered scaffolds [79, 87, 88]; commonsense tasks yield oscillatory paths [89, 90, 91]. nDNA aligns with interpretable AI goals [92] and geometric decoding approaches [93].
This corpus dependence is not arbitrary noise – it reflects the model’s learned latent regulatory logic, analogous to the combinatorial control of gene regulatory networks that ensures context-sensitive yet robust gene expression [68, 62]. Just as developmental disorders arise when regulatory circuits misfire [64], misalignment or hallucination in LLMs can be traced to latent trajectories that diverge from expected scaffolding. nDNA analysis, therefore, does not merely characterize model geometry – it offers a tool for interpretability, failure detection, and safe alignment.
Corpus dependence in nDNA is the expression of reasoning plasticity, bounded by universal latent priors much like gene networks balance flexibility with functional coherence.
Moreover, the universality of nDNA’s foundational structure – its pretrained manifold, architectural symmetries, and core alignment priors – provides the stabilizing grammar that constrains corpus-specific scaffolds within meaningful reasoning spaces [75, 77]. This is the latent equivalent of biology’s genetic code and conserved transcriptional machinery: an invariant substrate that supports functional diversity without sacrificing coherence. By quantifying how nDNA paths bend, stretch, or steer in response to task demands, we can map the model’s cognitive landscape – and determine when it traces human-aligned reasoning or drifts into failure modes.
What the genome is to life’s functional unity, nDNA is to the model’s reasoning coherence: a universal code that binds diversity into stability, and complexity into interpretability.
| Layer | DNA (Biology) | nDNA (LLM) |
|---|---|---|
| Universal code | Codon mapping \(\phi: \Sigma^3 \to \mathcal{A}\), kernel \(\neq \emptyset\), redundancy ensures error tolerance [62] | Pretrained latent manifold; symmetries \(G_{\text{LLM}} \subset \text{Aut}(V)\); generalization via equivariance [77] |
| Context regulator | Conditional \(P(\text{gene ON}|\text{TF, epi})\); Bayesian gene networks [68] | Conditional latent path \(P(h_1,\ldots,h_\ell|x)\); stochastic latent dynamics [71] |
| Path geometry | Minimal energy path \(\gamma^*\) in epigenetic landscape: \(\int_\gamma \lVert\nabla V\rVert \, ds\) [83] | Latent geodesic minimizing cost: \(\int_\gamma \lVert\nabla_\theta \log p(y\mid x)\rVert^2 \, ds\) [74] |
| Output mapping | Fiber bundle: \(\pi: E_{\text{gene}} \to B_{\text{cell}}\) | Fiber bundle: \(\pi: E_{\text{latent}} \to B_{\text{task}}\) |
nDNA Task Group Analysis
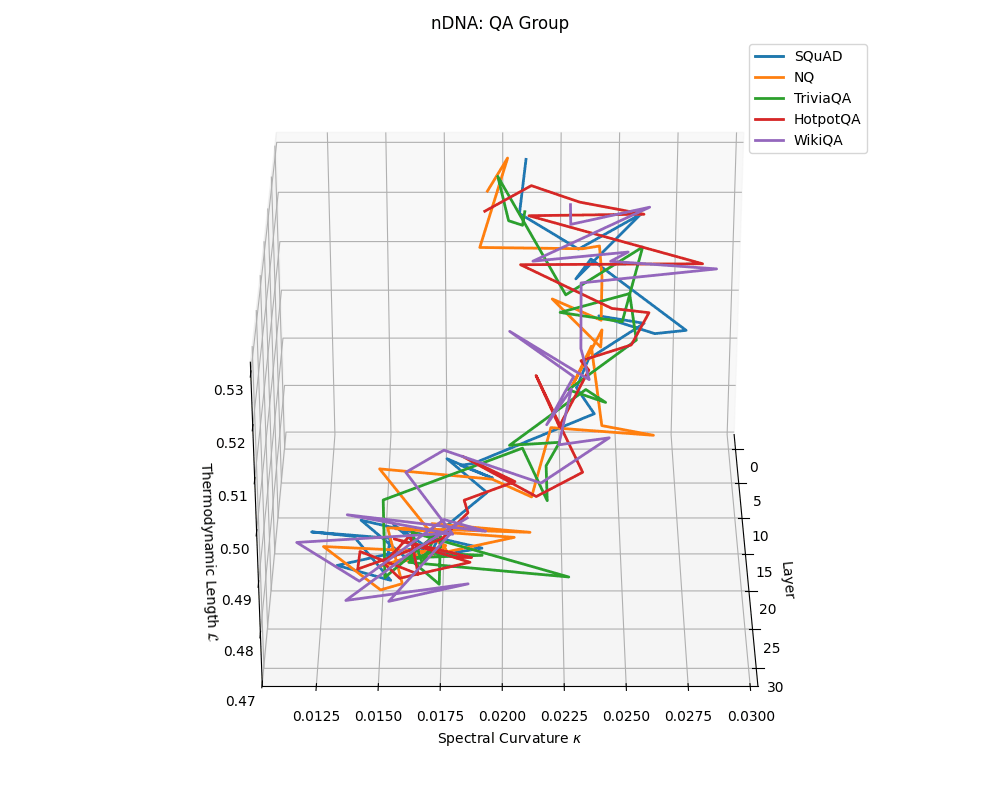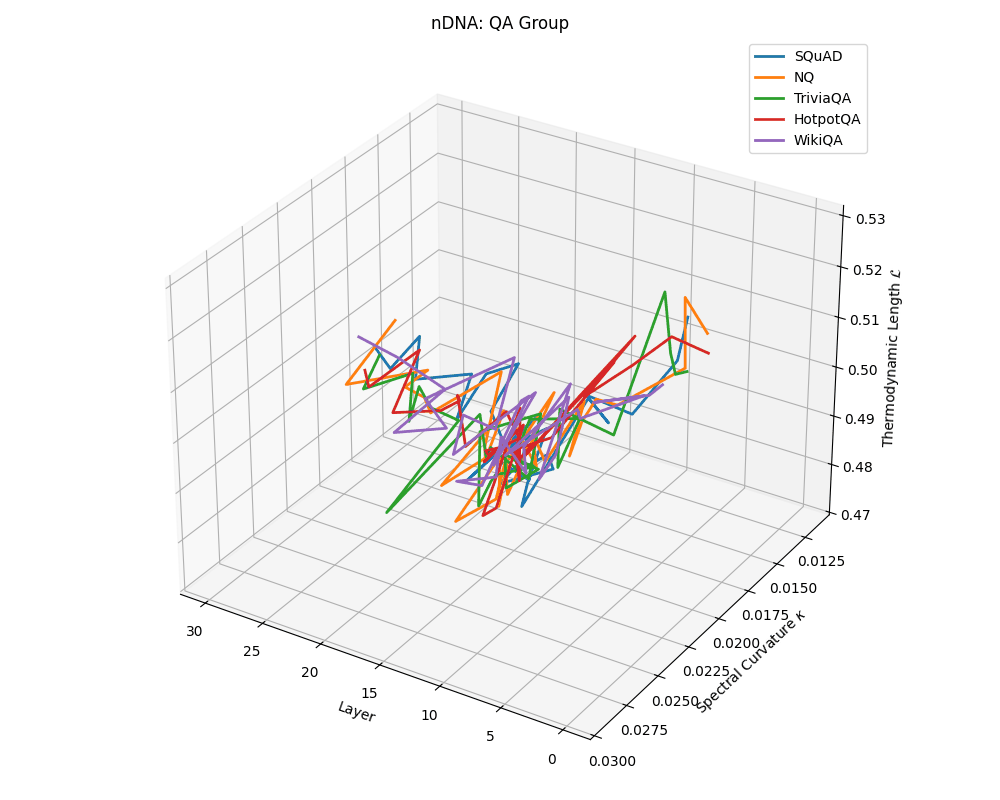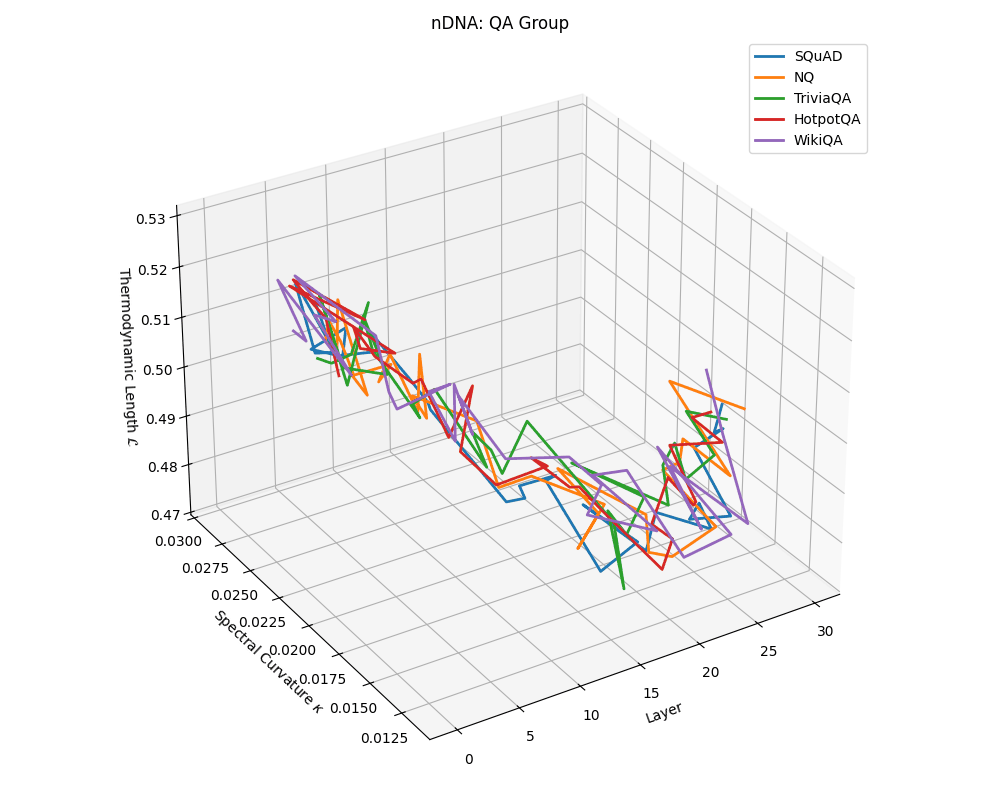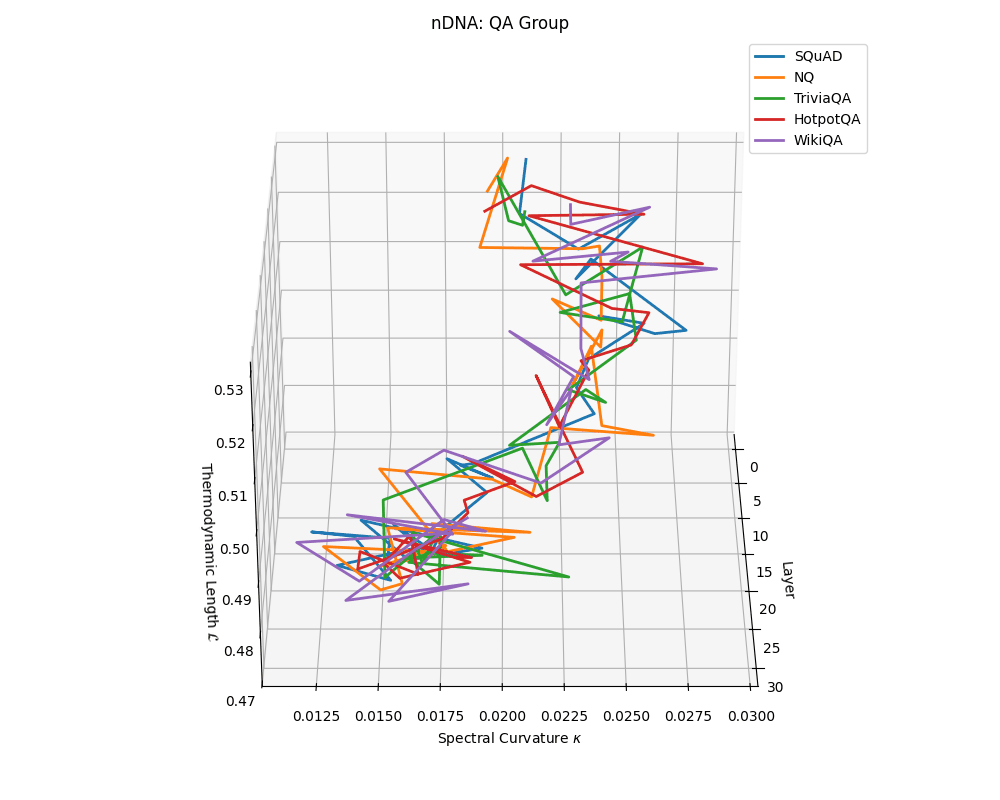
QA group nDNA trajectories: \(\kappa\) ranges \(\sim 0.012\)–\(0.03\), \(\mathcal{L} \sim 0.47\)–\(0.53\), \(\tau \sim 0.006\)–\(0.014\). Trajectories are compact and consistently shaped across datasets, reflecting shared task structure.
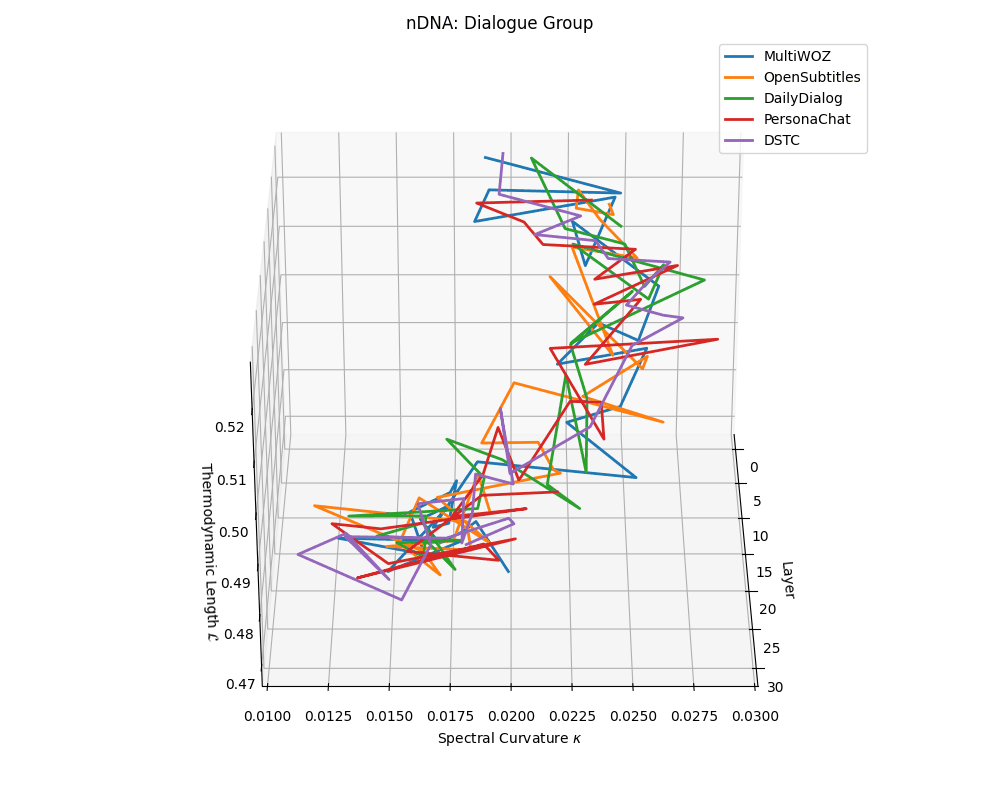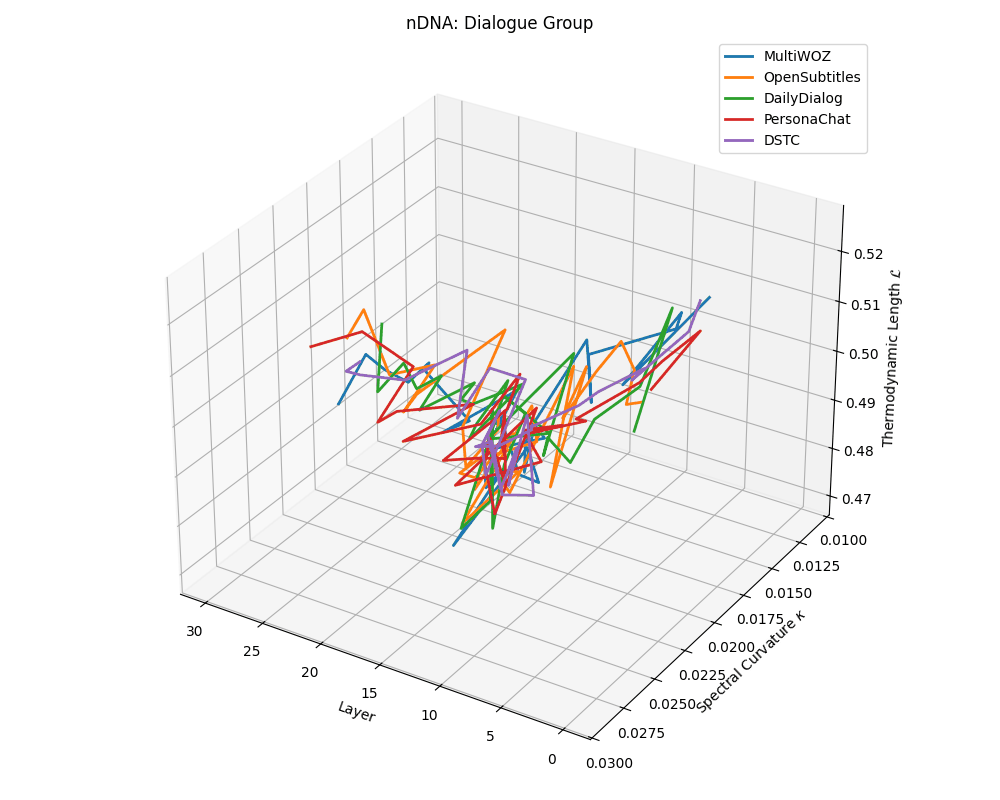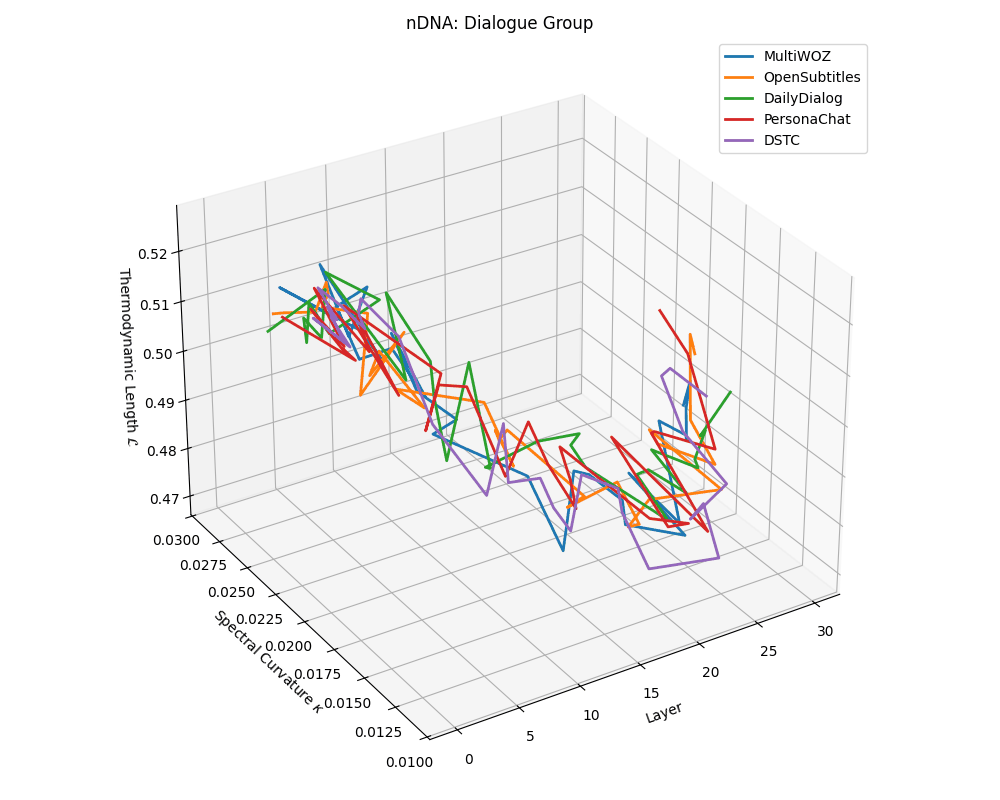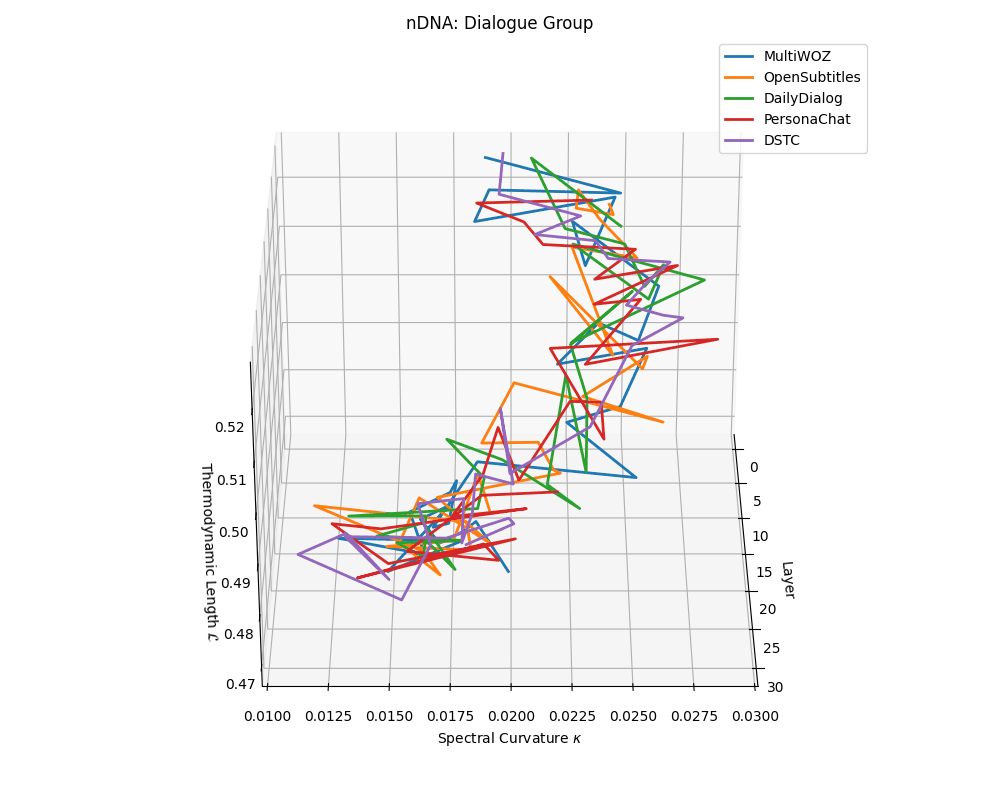
Dialogue group nDNA trajectories: \(\kappa\) ranges \(\sim 0.01\)–\(0.03\), \(\mathcal{L} \sim 0.47\)–\(0.53\), \(\tau \sim 0.006\)–\(0.014\). Trajectories are shallow and tightly clustered, reflecting low latent complexity typical of conversational flow.
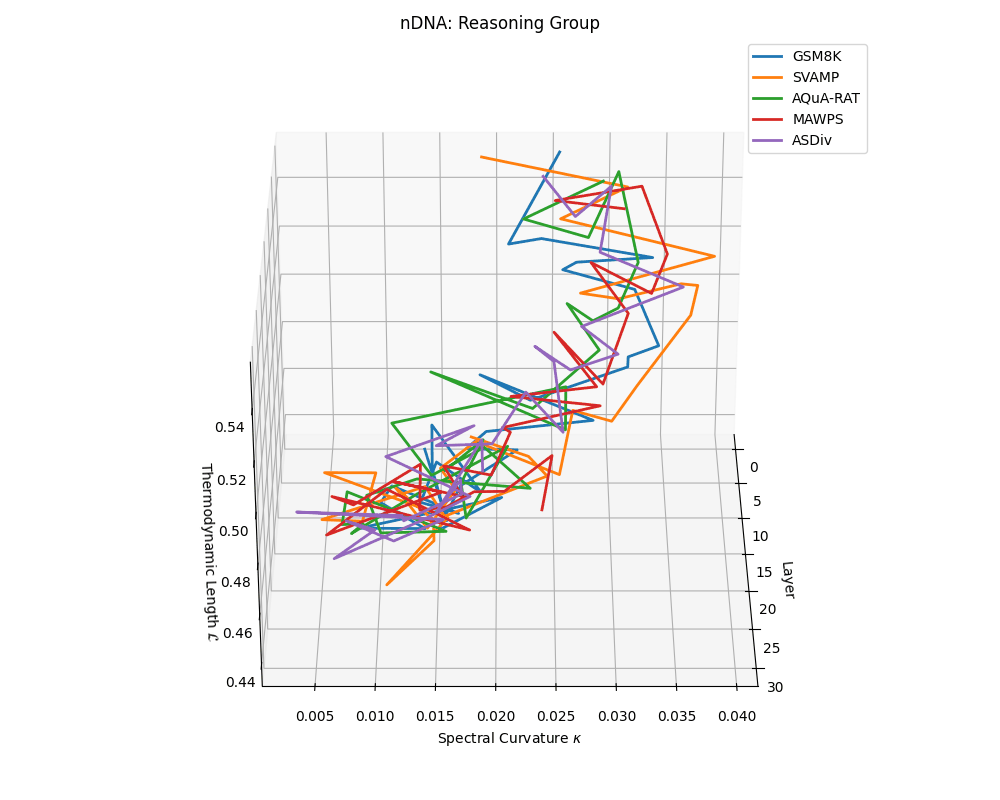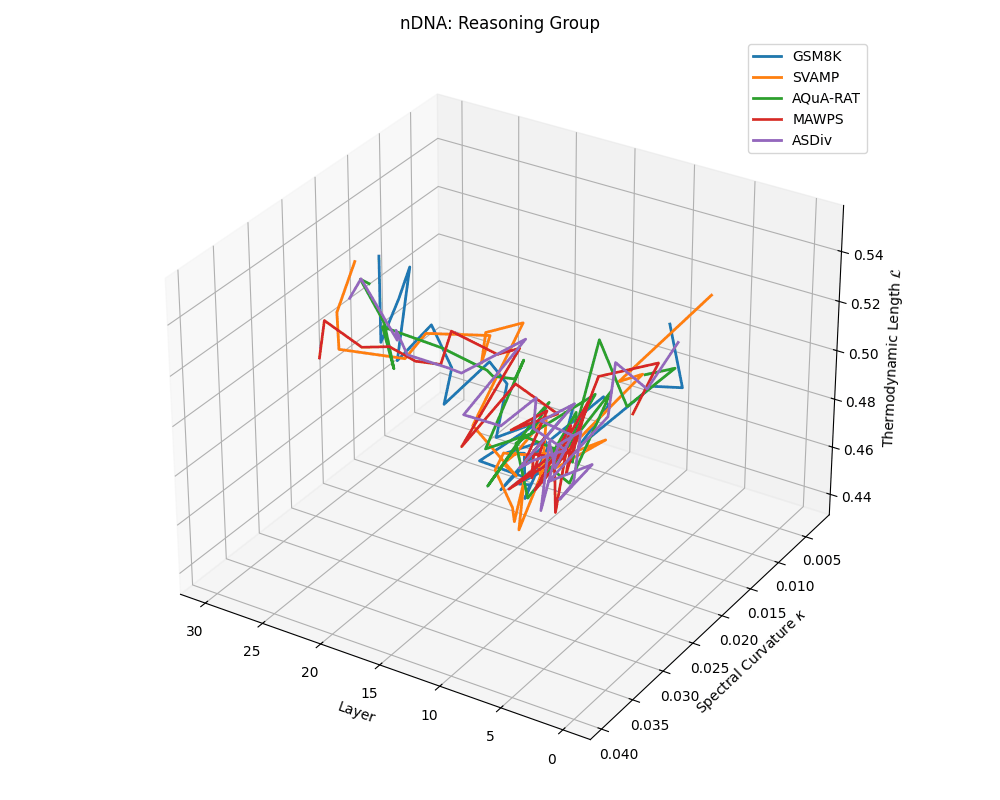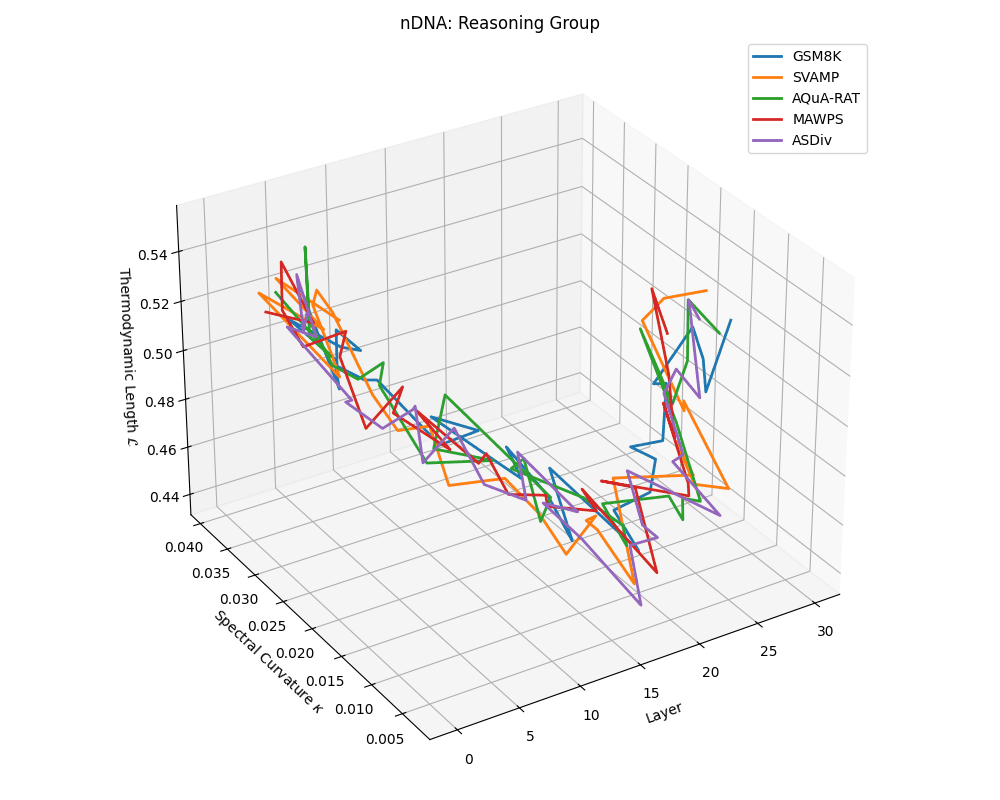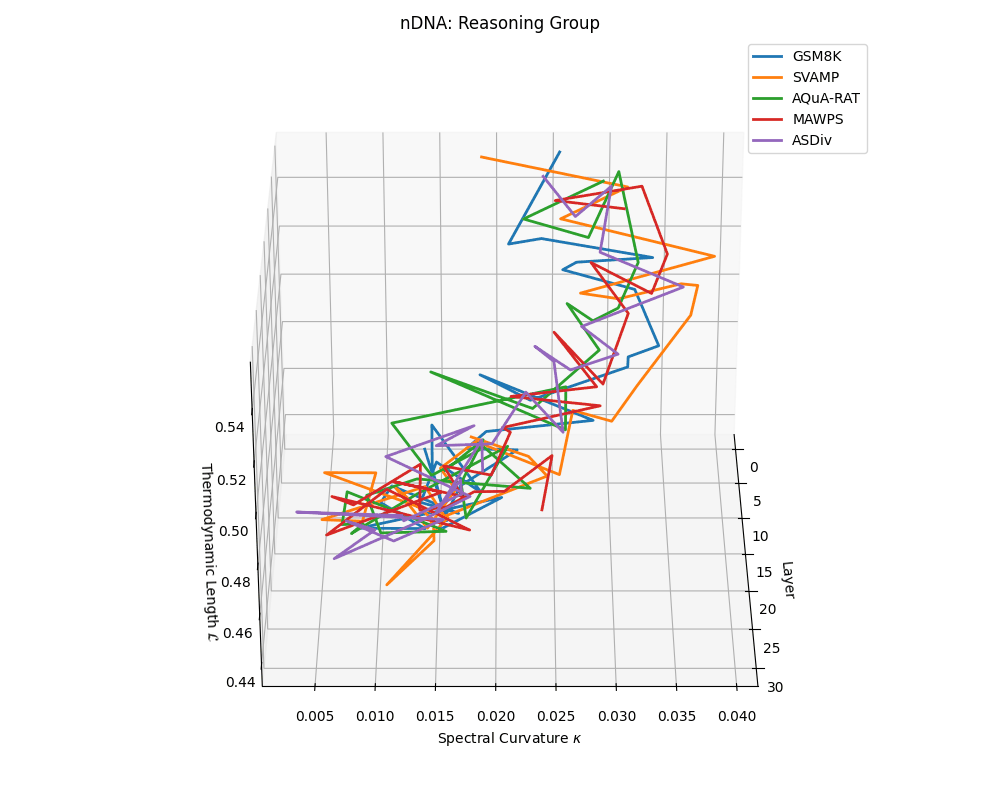
Reasoning group nDNA trajectories: \(\kappa\) ranges \(\sim 0.005\)–\(0.04\), \(\mathcal{L} \sim 0.44\)–\(0.56\), \(\tau \sim 0.002\)–\(0.018\). Trajectories show greater spread and complexity, reflecting multi-step reasoning scaffolding.
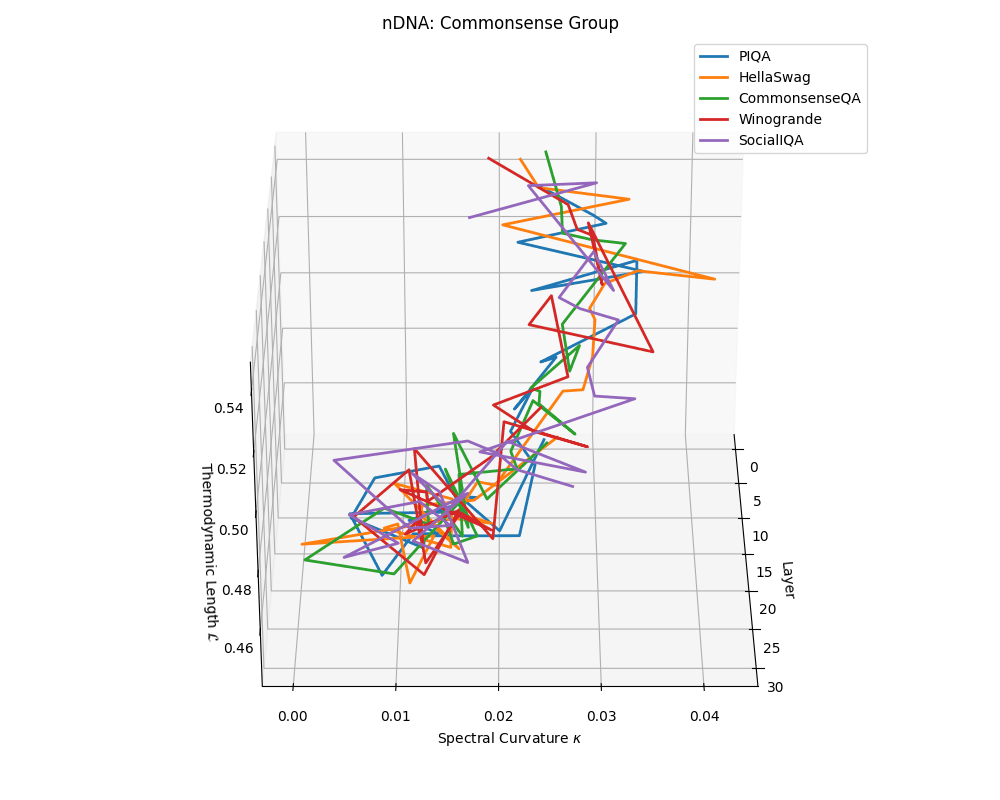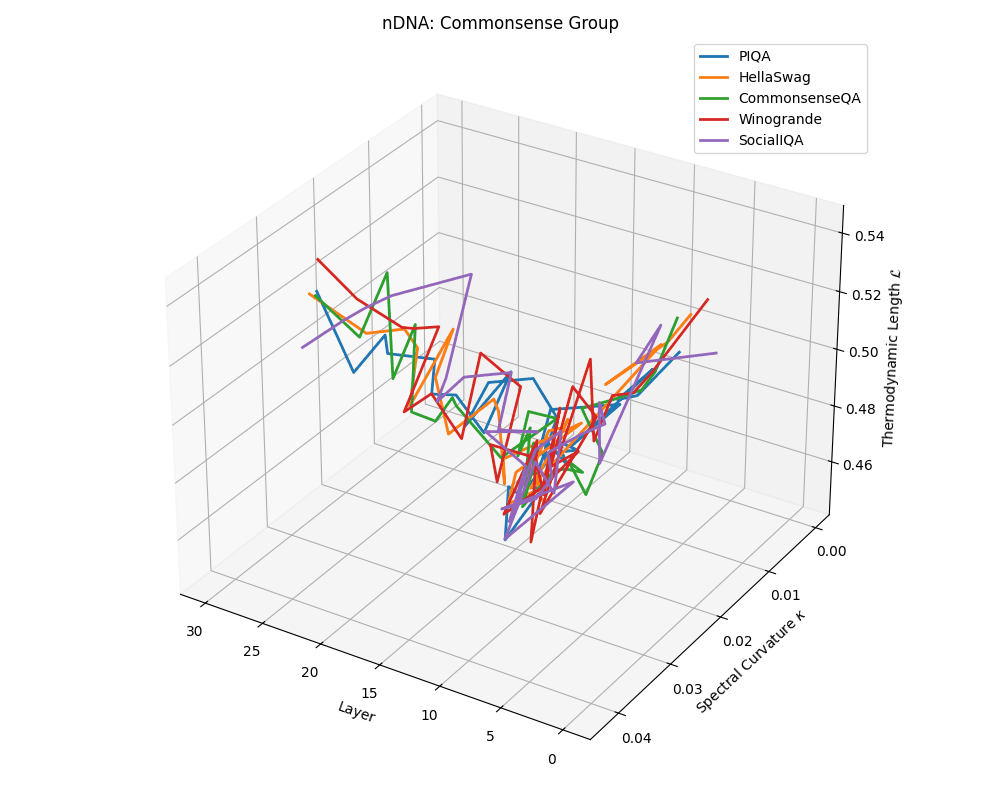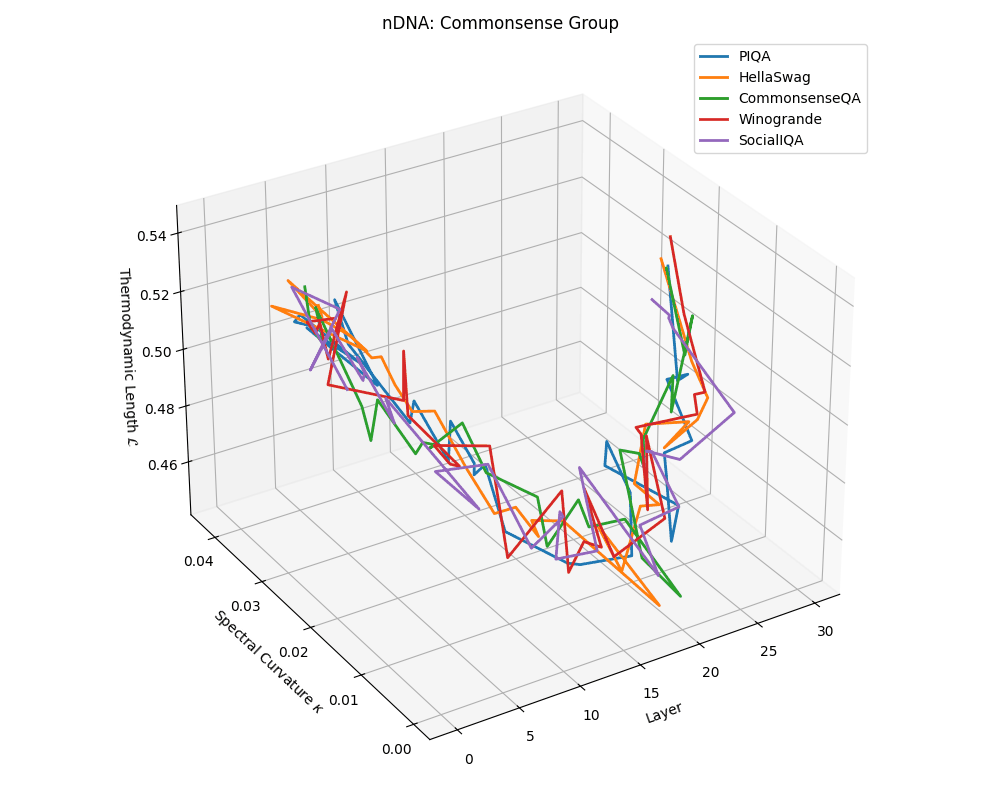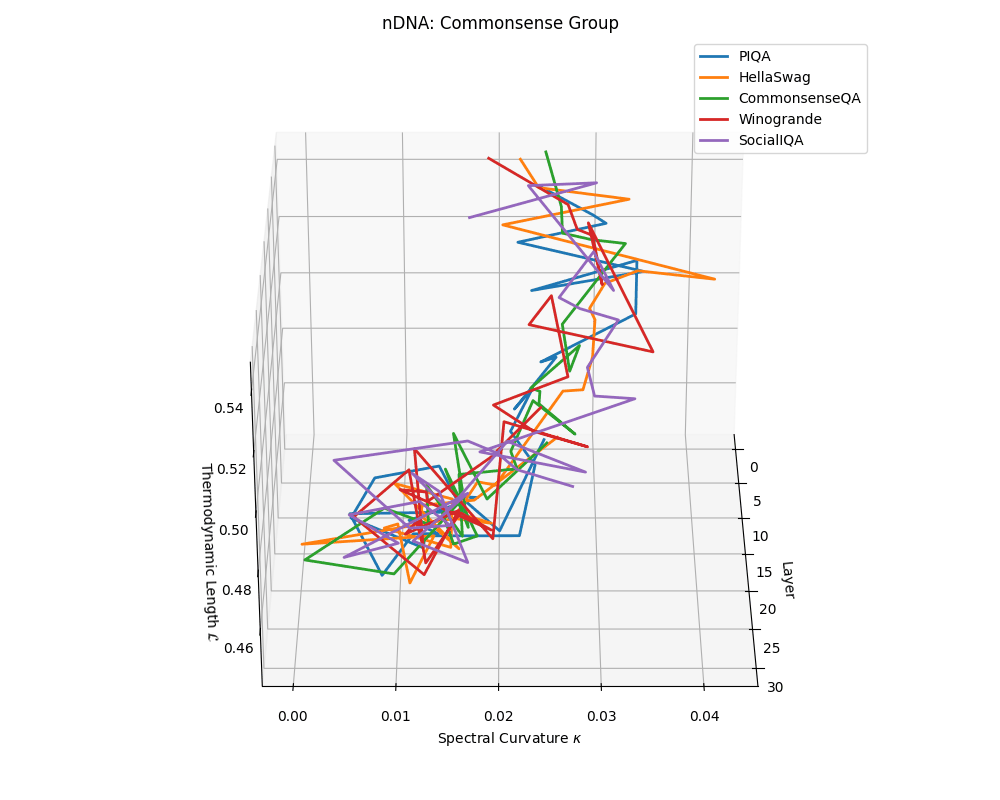
Commonsense group nDNA trajectories: \(\kappa\) ranges \(\sim 0.00\)–\(0.04\), \(\mathcal{L} \sim 0.44\)–\(0.54\), \(\tau \sim 0.004\)–\(0.018\). Trajectories are intermediate in complexity, reflecting varied latent demands of commonsense reasoning.
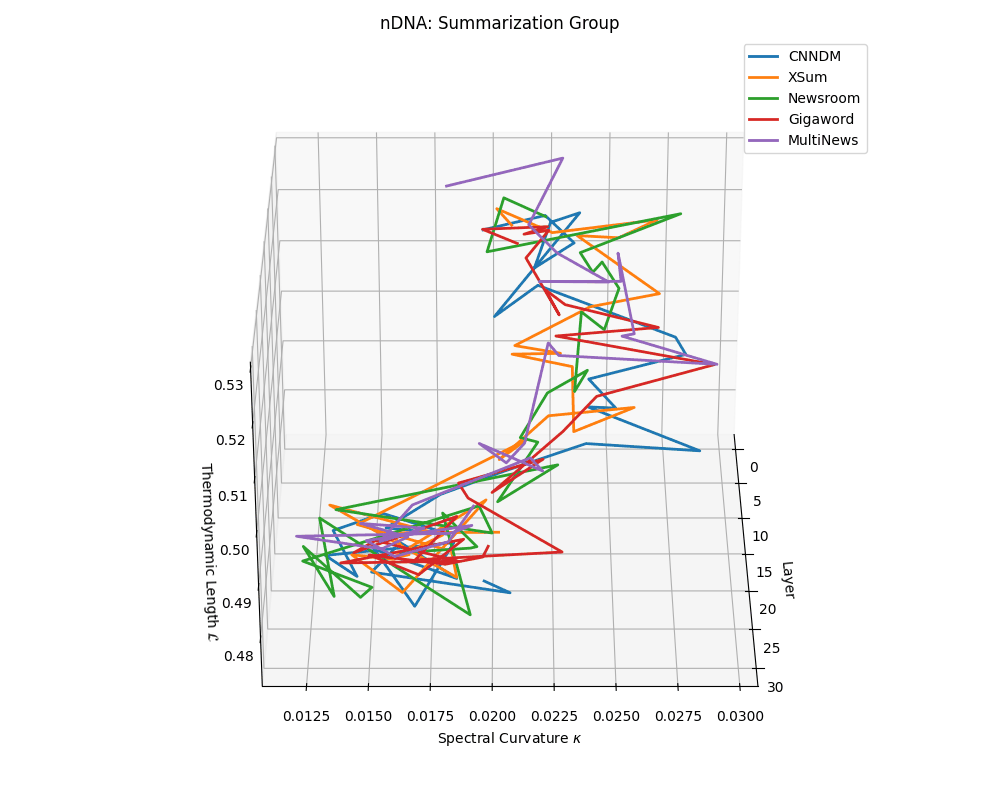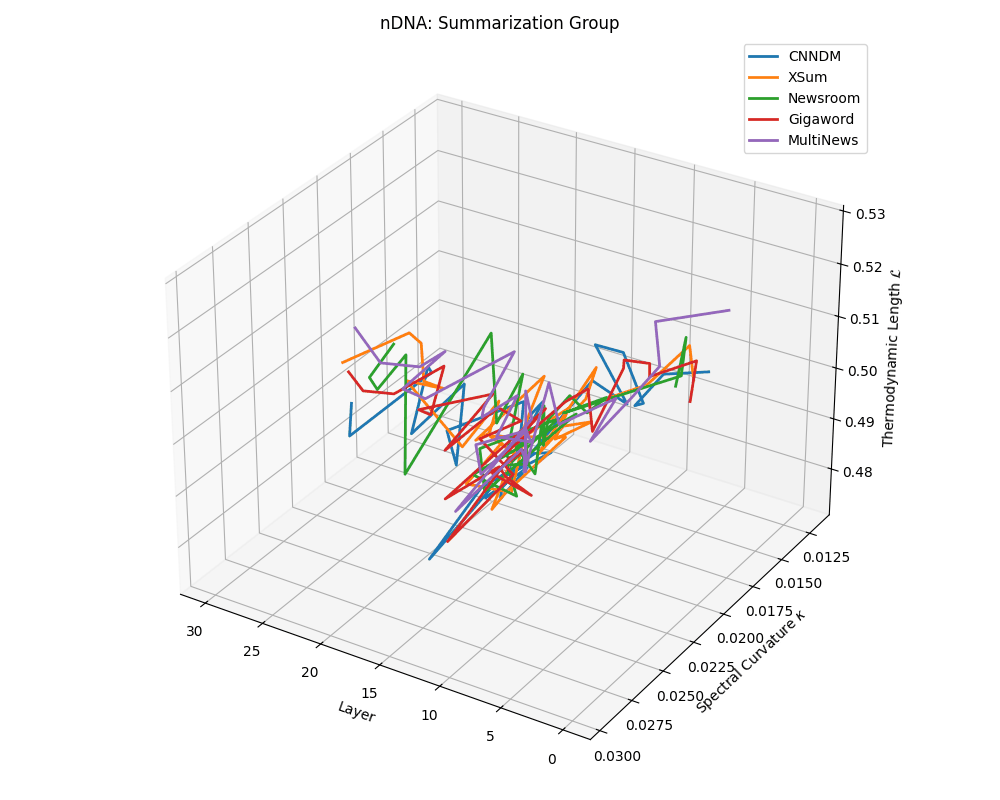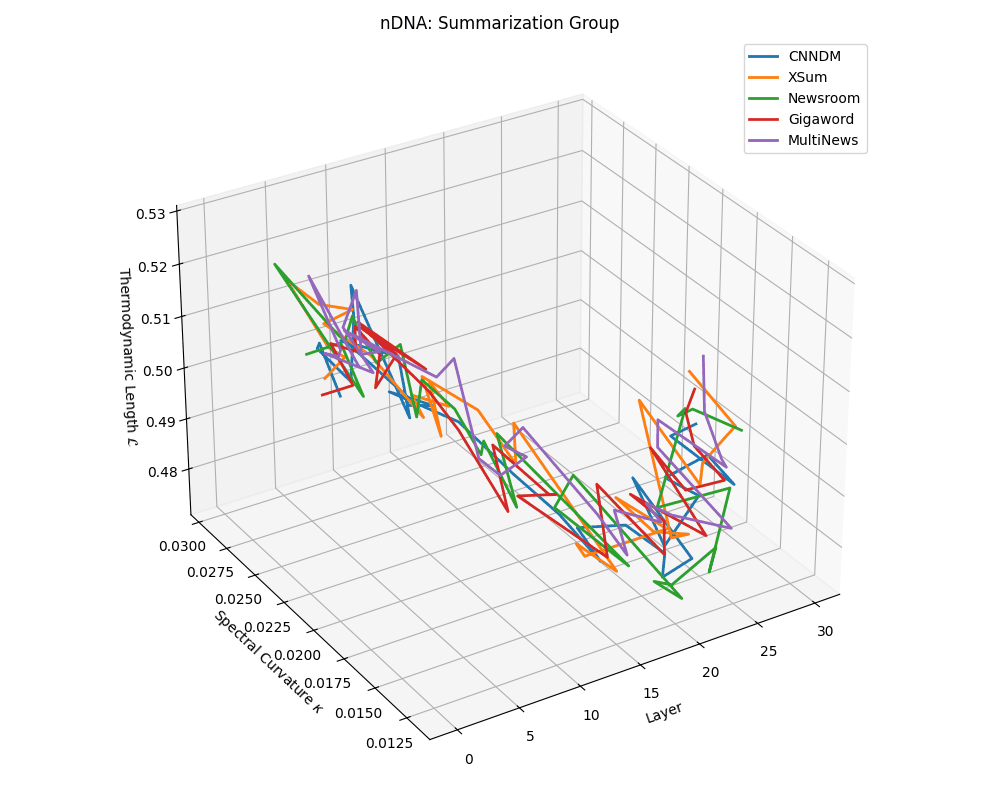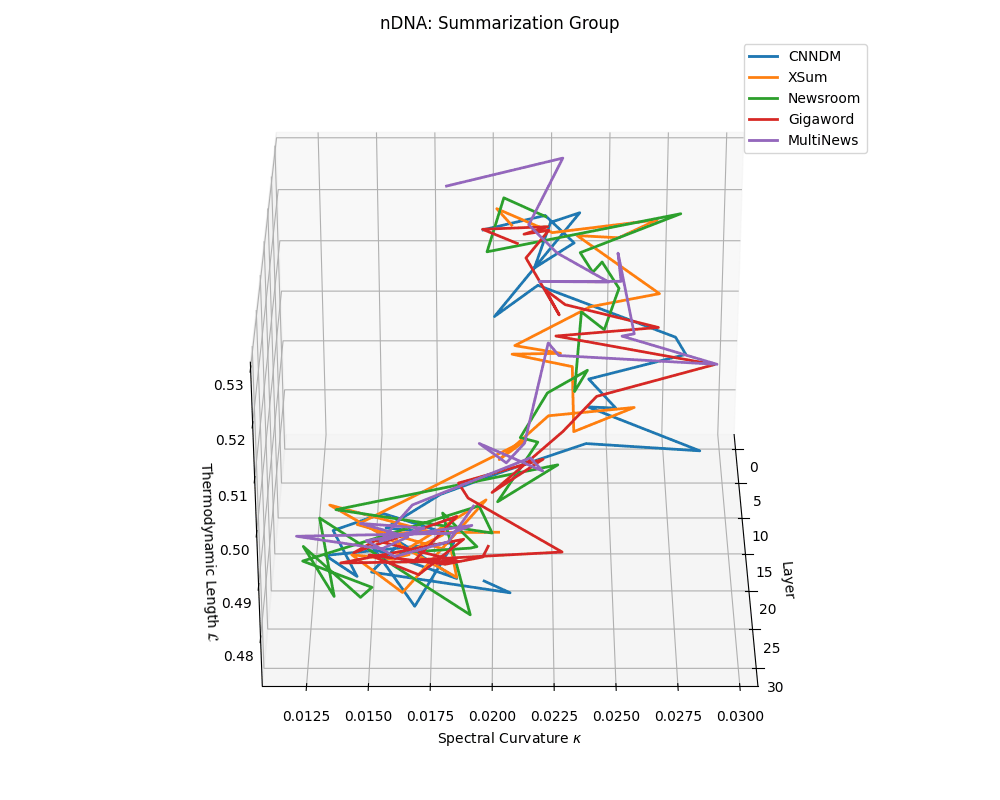
nDNA trajectories across LLaMA vs. task groups. Each subplot visualizes spectral curvature \((\kappa_\ell)\), thermodynamic length \((\mathcal{L}_\ell)\), and belief vector norm \((\lVert\mathbf{v}_\ell^{(c)}\rVert)\) layer-wise trajectories for representative datasets. The structured variation illustrates that corpus dependence in nDNA is meaningful and interpretable, reflecting task complexity rather than random noise. QA and dialogue tasks activate compact, smooth latent scaffolds with low curvature and modest belief steering; reasoning tasks exhibit broader, more intricate geometry, with increasing curvature, longer latent length, and stronger belief vector dynamics. Commonsense tasks show intermediate complexity with oscillatory scaffolding, reflecting ambiguity and contextual switching. This figure demonstrates the core takeaway of our section: like biological DNA, nDNA expresses differently in context, but remains bound by universal latent priors that ensure coherence, generalization, and alignment.
References
[1] Belrose, Jacob, Chan, Amanda, and others “A Mechanistic Interpretability Analysis of Grokking” arXiv preprint arXiv:2301.05217 (2023).
[2] Geva, Mor, Schuster, Tal, and others “Transformer feed-forward layers are key-value memories” Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing (2022).
[3] Dai, Zihang, Lin, Xuezhi, and others “Knowledge neurons in pretrained transformers” arXiv preprint arXiv:2104.08696 (2023).
[4] Liu, Nelson and others “Hidden Progress in Language Models” arXiv preprint arXiv:2305.04388 (2023).
[5] Zhou, Ben and others “On Alignment Drift in Large Language Models” arXiv preprint arXiv:2310.02979 (2023).
[6] Ganguli, Deep and others “Reducing sycophancy in large language models via self-distillation” arXiv preprint arXiv:2305.17493 (2023).
[7] Wu, Z. and others “Seamless: Robust distillation of large models” ICML (2024).
[8] Xu, J. and others “Aligning large language models with iterative feedback” ICLR (2023).
[9] Jacobs, Rachel, Uesato, Jonathan, and others “Evaluation-Aware Language Models” arXiv preprint arXiv:2406.02583 (2024).
[10] Perez, Ethan, Ringer, Sam, and others “Discovering latent knowledge in language models without supervision” arXiv preprint arXiv:2212.03827 (2022).
[11] Liu, Nelson F. and others “Lost in the Middle: How Language Models Use Long Contexts” arXiv preprint arXiv:2307.03172 (2023).
[12] Bai, Yuntao and others “Constitutional AI: Harmlessness from AI Feedback” arXiv preprint arXiv:2212.08073 (2023).
[13] Mukherjee, Subhadeep, Das, Amitava, and others “Cultural Inconsistency and Value Conflict in Multilingual Language Models” arXiv preprint arXiv:2404.08730 (2024).
[14] Chen, Daphne Ippolito and others “When Can AI Systems Disagree with Humans? Evaluating Multilingual Alignment” arXiv preprint arXiv:2309.00946 (2023).
[15] Chiang, Cheng and others “Can Language Models Learn with Less? A Study on Fine-Tuning Alignment” arXiv preprint arXiv:2309.01855 (2023).
[16] Bakker, Tom and others “Uniting Model Merging and Distillation: Towards Unified Neural Inheritance” arXiv preprint arXiv:2402.00999 (2024).
[17] Garipov, Timur, Izmailov, Pavel, and others “Loss Surfaces, Mode Connectivity, and Fast Ensembling of Deep Neural Networks” Advances in Neural Information Processing Systems (2018). https://arxiv.org/abs/1802.10026
[18] Draxler, Felix, Veschgini, Kambis, and others “Essentially No Barriers in Neural Network Energy Landscape” Proceedings of the 35th International Conference on Machine Learning (2018). https://proceedings.mlr.press/v80/draxler18a.html
[19] Li, Hao, Xu, Zheng, and others “Visualizing the Loss Landscape of Neural Nets” Advances in Neural Information Processing Systems (2018). https://papers.nips.cc/paper/2018/hash/a41b3bb3e6b050b6c9067c67f663b915-Abstract.html
[20] Entezari, Rahim, Sedghi, Hanie, and others “The Role of Permutation Invariance in Linear Mode Connectivity of Neural Networks” International Conference on Learning Representations (2022). https://arxiv.org/abs/2110.06296
[21] Ainsworth, Samuel K., Hayase, Jonathan, and others “Git Re-Basin: Merging Models modulo Permutation Symmetries” International Conference on Learning Representations (ICLR) (2023). https://openreview.net/forum?id=CQsmMYmlP5T
[22] Wortsman, Mitchell, Ilharco, Gabriel, and others “Model soups: averaging weights of multiple fine-tuned models improves accuracy without increasing inference time” Proceedings of the 39th International Conference on Machine Learning (ICML) (2022). https://arxiv.org/abs/2205.05638
[23] Efron, Bradley “Defining the Curvature of a Statistical Problem (with Applications to Second Order Efficiency)” The Annals of Statistics (1975). https://projecteuclid.org/journals/annals-of-statistics/volume-3/issue-6/defining-the-curvature-of-a-statistical-problem-with-applications-to-second-order-efficiency/10.1214/aos/1176343282
[24] Amari, Shun-ichi and Nagaoka, Hiroshi “Methods of information geometry” arXiv preprint (2000).
[25] Amari, Shun-ichi “Information geometry and its applications” Applied Mathematical Sciences (2016).
[26] Jain, Sarthak and Wallace, Byron C. “Attention is not Explanation” Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (2019). https://aclanthology.org/N19-1357/
[27] Serrano, Sofia and Smith, Noah A. “Is Attention Interpretable?” Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics (2019). https://aclanthology.org/P19-1282/
[28] Michel, Paul, Levy, Omer, and others “Are sixteen heads really better than one?” Advances in Neural Information Processing Systems (NeurIPS) (2019).
[29] Voita, Elena, Talbot, David, and others “Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned” Proceedings of ACL (2019).
[30] Clark, Kevin, Khandelwal, Urvashi, and others “What Does {BERT} Look At? An Analysis of {BERT}’s Attention” Proceedings of the 2019 ACL Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP (2019). https://aclanthology.org/W19-4828/
[31] Kovaleva, Olga, Romanov, Alexey, and others “Revealing the Dark Secrets of {BERT}” Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP) (2019). https://aclanthology.org/D19-1445
[32] Abnar, Samira and Zuidema, Willem “Quantifying Attention Flow in Transformers” Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (2020). https://aclanthology.org/2020.acl-main.385
[33] Geva, Mor, Schuster, Roei, and others “Transformer Feed-Forward Layers Are Key-Value Memories” Proceedings of EMNLP (2021). https://aclanthology.org/2021.emnlp-main.446/
[34] Adebayo, Julius, Gilmer, Justin, and others “Sanity Checks for Saliency Maps” Advances in Neural Information Processing Systems 31 (NeurIPS 2018) (2018). https://proceedings.neurips.cc/paper/2018/hash/294a8ed24b1ad22ec2e7efea049b8737-Abstract.html
[35] Jacovi, Alon and Goldberg, Yoav “Towards Faithfully Interpretable NLP Systems: How Should We Define and Evaluate Faithfulness?” Proceedings of ACL (2020). https://aclanthology.org/2020.acl-main.386/
[36] Tenney, Ian, Das, Dipanjan, and others “BERT rediscovers the classical NLP pipeline” Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics (2019).
[37] Sivak, David A and Crooks, Gavin E “Thermodynamic metrics and optimal paths” Physical Review Letters (2012).
[38] Hyv{"a}rinen, Aapo “Estimation of Non-Normalized Statistical Models by Score Matching” Journal of Machine Learning Research (2005). https://jmlr.org/papers/v6/hyvarinen05a.html
[39] Farzam, Amir, Subramani, Akshay, and others “Ricci Curvature Reveals Alignment Dynamics in Language Models” ICLR (2024).
[40] Cho, Kyunghyun and others “Mixed Curvature Geometry in Large Language Models” arXiv preprint arXiv:2310.04890 (2023).
[41] Gasteiger, Johannes, Becker, Florian, and others “GemNet: Universal Directional Graph Neural Networks for Molecules” NeurIPS (2021).
[42] Xu, Yifan and Tong, Hanghang “Spherical Graph Neural Networks for Learning on Non-Euclidean Structures” ICLR (2022).
[43] Konf, Anna and Zhang, Yuhang “Hierarchical Spectral Networks for Structured Reasoning” ACL (2021).
[44] Ying, Rex, Tancik, Matthew, and others “SE(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials” NeurIPS (2021). https://proceedings.neurips.cc/paper_files/paper/2021/file/2e7480b033cddcfba40cbed8d8b2c4ec-Paper.pdf
[45] Hu, Zexuan, Li, Qi, and others “Learning Lie Algebra Representations in Transformers” NeurIPS (2022). https://proceedings.neurips.cc/paper_files/paper/2022/file/3a1b9185290a2c576a8cc4eecdfd24f9-Paper-Conference.pdf
[46] Hess, William, Rahimi, Ali, and others “Spectral Regularization for Stable Representation Learning” ICML (2023). https://proceedings.mlr.press/v202/hess23a/hess23a.pdf
[47] Wang, Qingyun and others “GeomTransformer: Geometry-Equivariant Attention for Molecular Graphs” ICLR (2021).
[48] Raposo, Tiago and Xu, Muhao “Spectral Geometry in Language Models” arXiv preprint arXiv:2308.00042 (2023). https://arxiv.org/abs/2308.00042
[49] Crooks, Gavin E “Measuring thermodynamic length” Physical Review Letters (2007).
[50] Oliviero, Daniele, Bacciu, Davide, and others “Thermodynamics of Learning: Energy-Based Viewpoints and Information Geometry in Deep Learning” Proceedings of the 40th International Conference on Machine Learning (ICML) (2023).
[51] Wagner, Henrik and Bubeck, Sébastien “Thermodynamic Metrics Reveal Capacity Allocation in Transformers” arXiv preprint arXiv:2306.13052 (2023).
[52] Wang, Ziwei, Xu, Yichao, and others “Cultural bias in large language models: A survey” arXiv preprint arXiv:2311.05691 (2023).
[53] Shen, Sheng and others “The Geometry of Belief in Language Models” arXiv preprint arXiv:2305.12355 (2023).
[54] Arora, Akhila, Goyal, Tushar, and others “Stereoset: Measuring stereotypical bias in pretrained language models” TACL (2023).
[55] Bommasani, R. and others “Foundation models: Past, present, and future” arXiv preprint arXiv:2309.00616 (2023).
[56] Peng, Baolin, Wang, Li, and others “Culturally aligned language modeling: Methods and benchmarks” ACL (2024).
[57] Laurens, Ethan and others “The Ethics of Alignment: Towards Culturally Inclusive Foundation Models” Proceedings of the AAAI Conference on Artificial Intelligence (2024).
[58] Kang, Junjie and Liu, Emily “Fairness Across Cultures in NLP” ACL (2024).
[59] de Vries, Harm and Sharma, Aarushi “Latent Bias Projection in Transformers” EMNLP (2023).
[60] Gao, Xiaozhong and Huang, Yiwen “Tracing Value Attribution in Foundation Models” NeurIPS (2023).
[61] Alberts, Bruce, Johnson, Alexander, and others “Molecular Biology of the Cell” arXiv preprint (2014).
[62] Lewin, Benjamin, Krebs, Jocelyn E, and others “Genes XI” arXiv preprint (2013).
[63] Bird, Adrian “Perceptions of epigenetics” Nature (2007).
[64] Davidson, Eric H. “The Regulatory Genome: Gene Regulatory Networks In Development And Evolution” arXiv preprint (2006).
[65] Lambert, Samuel A., Jolma, Arttu, and others “The human transcription factors” Cell (2018).
[66] Clapier, Cedric R., Iwasa, Janet, and others “Mechanisms of action and regulation of ATP-dependent chromatin-remodelling complexes” Nature Reviews Molecular Cell Biology (2017).
[67] Dekker, Job and Mirny, Leonid “Exploring the three-dimensional organization of genomes: interpreting chromatin interaction data” Nature Reviews Genetics (2013).
[68] Alon, Uri “An Introduction to Systems Biology: Design Principles of Biological Circuits” arXiv preprint (2006).
[69] Thurman, Robert E., Rynes, Eric, and others “The accessible chromatin landscape of the human genome” Nature (2012).
[70] Olah, Chris, Satyanarayan, Arvind, and others “Zoom In: An introduction to circuits” arXiv preprint (2020). https://distill.pub/2020/circuits/zoom-in/
[71] Geva, Mor, Schuster, Tal, and others “Transformer feed-forward layers are key-value memories” Proceedings of EMNLP (2021).
[72] Beltagy, Iz, Peters, Matthew E., and others “Longformer: The Long-Document Transformer” arXiv preprint arXiv:2004.05150 (2020).
[73] Belkin, Mikhail, Hsu, Daniel, and others “Reconciling modern machine-learning practice and the classical bias–variance trade-off” Proceedings of the National Academy of Sciences (2019).
[74] Still, Susanne “Thermodynamic cost and benefit of memory” Physical Review Letters (2012).
[75] Vaswani, Ashish, Shazeer, Noam, and others “Attention is all you need” Proceedings of NeurIPS (2017).
[76] Mikolov, Tomas, Sutskever, Ilya, and others “Distributed representations of words and phrases and their compositionality” NeurIPS (2013).
[77] Bommasani, Rishi, Hudson, Drew A, and others “On the opportunities and risks of foundation models” arXiv preprint arXiv:2108.07258 (2021).
[78] Cobbe, Karl, Kosaraju, Vineet, and others “Training verifiers to solve math word problems” arXiv preprint arXiv:2110.14168 (2021).
[79] Budzianowski, Paweł, Wen, Tsung-Hsien, and others “MultiWOZ–A large-scale multi-domain wizard-of-oz dataset for task-oriented dialogue modelling” Proceedings of EMNLP (2018).
[80] Rajpurkar, Pranav, Zhang, Jian, and others “SQuAD: 100,000+ questions for machine comprehension of text” Proceedings of EMNLP (2016).
[81] Pfeiffer, Jonas, Kamath, Ankur, and others “AdapterFusion: Non-Destructive Task Composition for Transfer Learning” EACL (2021).
[82] Marioni, John C, Mason, Christopher E, and others “RNA-seq: An assessment of technical reproducibility and comparison with gene expression arrays” Genome research (2008).
[83] Waddington, Conrad Hal “The strategy of the genes: a discussion of some aspects of theoretical biology” Allen & Unwin (1957).
[84] Kwiatkowski, Tom, Palomaki, Jennimaria, and others “Natural Questions: A benchmark for question answering research” Proceedings of ACL (2019).
[85] Joshi, Mandar, Choi, Eunsol, and others “TriviaQA: A large scale distantly supervised challenge dataset for reading comprehension” Proceedings of ACL (2017).
[86] Patel, Shrey Desai, Chen, Zi, and others “Are NLP models really robust? Evaluating and enhancing the robustness of NLP models for numerical reasoning” Proceedings of EMNLP (2021).
[87] Li, Jiwei, Galley, Michel, and others “A persona-based neural conversation model” Proceedings of ACL (2016).
[88] Zhang, Saizheng, Dinan, Emily, and others “Personalizing dialogue agents: I have a dog, do you have pets too?” Proceedings of ACL (2018).
[89] Sap, Maarten, Le Bras, Ronan, and others “SocialIQA: Commonsense reasoning about social interactions” Proceedings of EMNLP (2019).
[90] Zellers, Rowan, Holtzman, Ari, and others “HellaSwag: Can a machine really finish your sentence?” Proceedings of ACL (2019).
[91] Talmor, Alon, Herzig, Jonathan, and others “CommonsenseQA: A question answering challenge targeting commonsense knowledge” Proceedings of NAACL-HLT (2019).
[92] Zhang, Qing, Yang, Wen, and others “Interpretable deep learning systems: A survey” arXiv preprint arXiv:1802.09945 (2018).
[93] Narayanan, S, Joshi, N, and others “Decoding language models: A geometric approach to interpretability” arXiv preprint arXiv:2105.06997 (2021).