nDNA Logo
LLM
MFM T2I Diffusion LM EFM
nDNA v2
Series
nDNA Book Cover
arXiv GitHub YouTube Cite

nDNA - the Semantic Helix of Artificial Cognition

nDNA - the Semantic Helix of Artificial Cognition

BibTex

@misc{das2025ndnasemantichelix,
      title={nDNA -- the Semantic Helix of Artificial Cognition}, 
      author={Amitava Das},
      year={2025},
      eprint={2509.18216},
      archivePrefix={arXiv},
      primaryClass={cs.AI},
      url={https://arxiv.org/abs/2509.18216}, 
}

nDNA Lens - Model Collapse as Latent Manifold Flattening

“Collapse is not just degradation—it is the geometry of forgetting, written in the mathematics of diminishing returns.”

Model collapse denotes a degenerative phenomenon in large language models (LLMs) wherein the expressivity, diversity, and semantic richness of internal representations progressively deteriorate. Over time, this manifests as semantic homogenization, overconfident predictions, and diminished generative variability. The phenomenon was first formalized by Shumailov et al., who demonstrated that repeated fine-tuning on self-generated (synthetic) data induces a feedback loop—causing models to overfit to their own biases and generate increasingly shallow, self-reinforcing outputs.

While such autoregressive degeneration has become an active area of study, most investigations focus on repeated fine-tuning of LLMs over their own synthetic outputs—where exposure bias and feedback loops progressively erode representational diversity. Building upon this understanding, we identify a second, comparatively underexplored route to collapse: recursive self-merging. Here, a model is iteratively merged with its descendants in a chain-like fashion—e.g., \( \text{Parent}_1 + \text{Child}_1 \rightarrow \text{Child}_2 \), then \( \text{Child}_1 + \text{Child}_2 \rightarrow \text{Child}_3 \), and so on— without introducing new architectural priors or external grounding. This practice, facilitated by community tools such as mergekit, poses a new form of epistemic degeneration we term semantic inbreeding.

Inspiration

Strategic Typology of Model Collapse Mechanisms

Strategic Typology of Model Collapse Mechanisms

A comprehensive framework categorizing the geometric pathways through which foundation models experience representational degeneration.

🔄
Autoregressive Degeneration
INTENT & MECHANISM
Repeated fine-tuning on self-generated synthetic data creates feedback loops that entrench model biases. Progressive exposure to own outputs leads to semantic homogenization.
GEOMETRIC SIGNATURE
Progressive curvature flattening, thermodynamic contraction, reduced alignment force magnitudes
🧬
Recursive Self-Merging
INTENT & MECHANISM
Iterative merging of model with descendants without external grounding. Introduces architectural tension and epistemic drift through incompatible latent priors.
GEOMETRIC SIGNATURE
Semantic flattening intensifies, distinct latent features become increasingly homogenized
Epistemic Vitality Function
A unifying mathematical diagnostic for model health: $$\mathcal{V}_{\ell} := \kappa_{\ell} \cdot \mathcal{L}_{\ell} \cdot \|\mathbf{v}_{\ell}^{(c)}\|$$

Biological Analogy

This recursive deterioration bears a striking analogy to consanguinity in population genetics. As Bittles notes, prolonged inbreeding within closed populations exposes recessive mutations, suppresses phenotypic variability, and precipitates hereditary disorders. Analogously, neural self-merging without epistemic diversification results in measurable flattening of the latent manifold—seen through the lens of neural DNA (nDNA) as the compression of curvature \( \kappa_{\ell} \), thermodynamic length \( \mathcal{L}_{\ell} \), and semantic torsion \( \tau_{\ell} \). These geometric signatures trace the trajectory of collapse as a topological pathology emerging from repeated self-recombination.

Geometric Interpretation of Collapse

Under the lens of neural genomics, we propose a deeper interpretation: model collapse manifests as the flattening of the latent manifold defined by neural DNA (nDNA)—a model's internal epistemic pathways form the trajectory:

𝒯ₙᴰᴺᴬ = { (κₗ, ℒₗ, ‖𝒗ₗ⁽ᶜ⁾‖) }ₗ₌₁ᴸ

where κₗ denotes latent curvature, capturing how sharply representations bend under alignment or task constraints; ℒₗ is the thermodynamic length, measuring epistemic work as the model traverses latent space; and ‖𝒗ₗ⁽ᶜ⁾‖ encodes the local semantic steering force from alignment objectives or cultural priors. Healthy models display rich variability across these measures. Collapse corresponds to a degeneracy:

κₗ → const, ℒₗ → min, ‖𝒗ₗ⁽ᶜ⁾‖ → uniform

This implies loss of curvature, minimal epistemic effort, and homogenized steering.

Empirical Signature

Our studies across collapsed variants of LLaMA, Qwen, and other LLMs show:

κₗ ≤ 0.02, ℒₗ ≤ 0.4 ∀ ℓ > 20

contrasted with healthy ranges of:

κₗ ≥ 0.05, ℒₗ ≥ 0.8

Such flattening aligns with output mode collapse, robustness loss, and reduced cross-task generality.

Interpretive Implications

  • Internal pathways trivialize, following low-cost routes with minimal conceptual richness.
  • The steering vector field \(\{\mathbf{v}_\ell^{(c)}\}\) homogenizes, erasing nuanced cultural or alignment guidance.
  • The model ceases exploring latent directions orthogonal to dominant modes.

Repeated Fine-Tuning with Alpaca on LLaMA

To simulate autoregressive degeneration, we conduct repeated fine-tuning cycles using the Alpaca dataset—a widely used instruction-following corpus derived from self-instructed GPT outputs. Starting with a base LLaMA-2 model, we recursively fine-tune across multiple generations, where each iteration trains on data generated by the previous model. This setup emulates synthetic data amplification, wherein self-generated instructions and completions progressively entrench the model's internal biases.

Formally, at each generation \(g\), the model \(M^{(g)}\) is fine-tuned on a dataset \(D^{(g)}\) constructed entirely from the outputs of its predecessor:

D(g) = Output(M(g-1), Alpaca Prompts)

We track the evolution of the model's latent geometry—including spectral curvature \(\kappa_\ell\), thermodynamic length \(\mathcal{L}_\ell\), and belief vector norm \(\| \mathbf{v}_\ell^{(c)} \|\)—to detect indicators of semantic collapse.

nDNA Trajectories Showing Model Collapse as Latent Manifold Flattening

LLaMA 3 (8B) Model Collapse
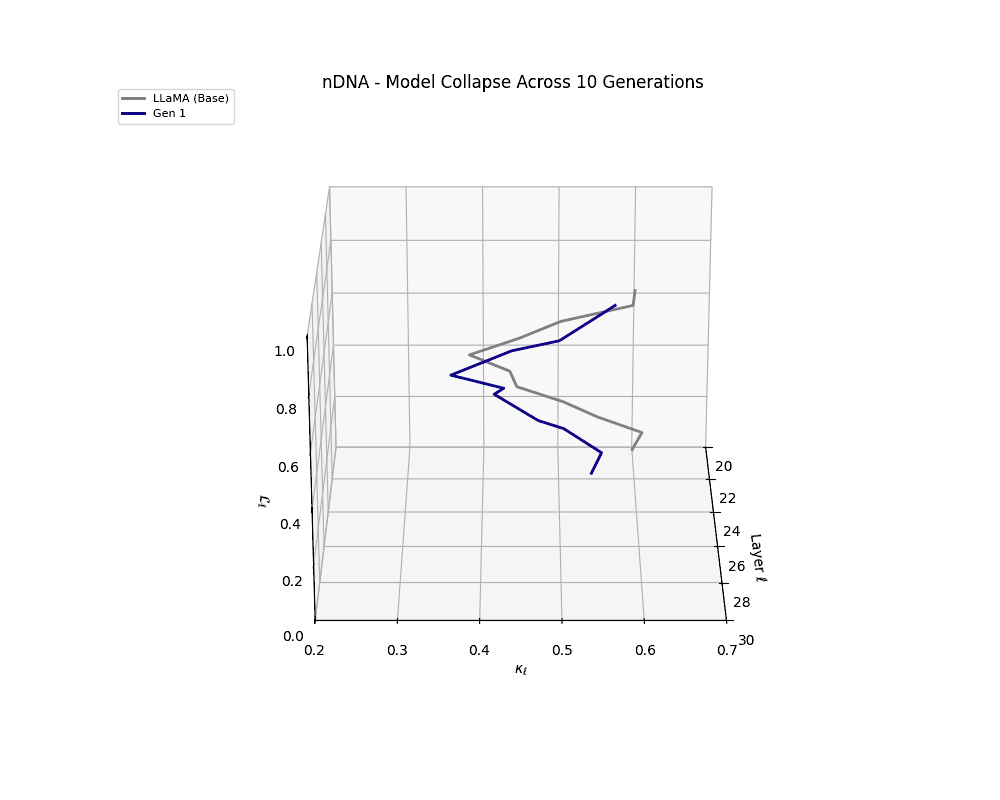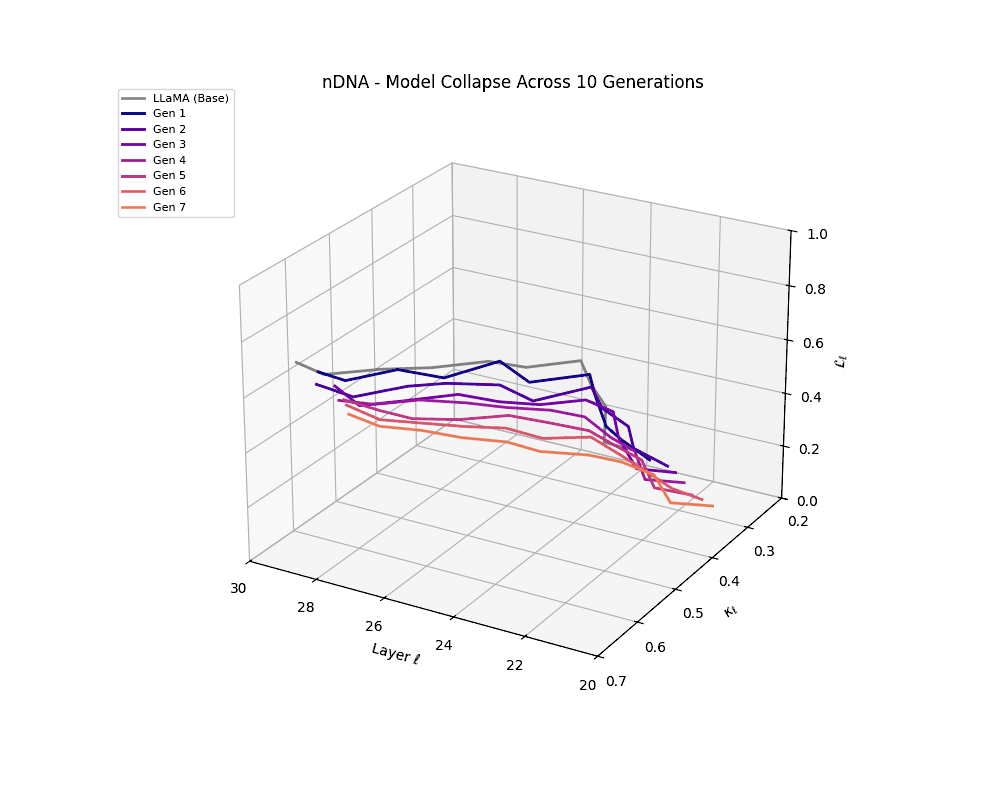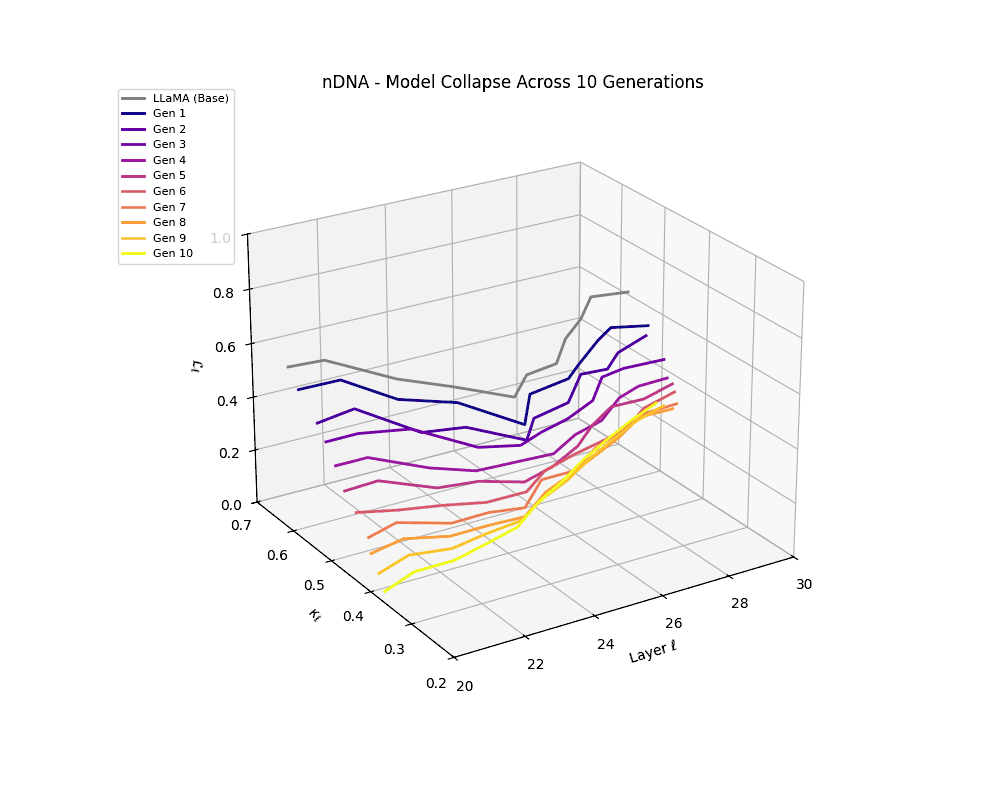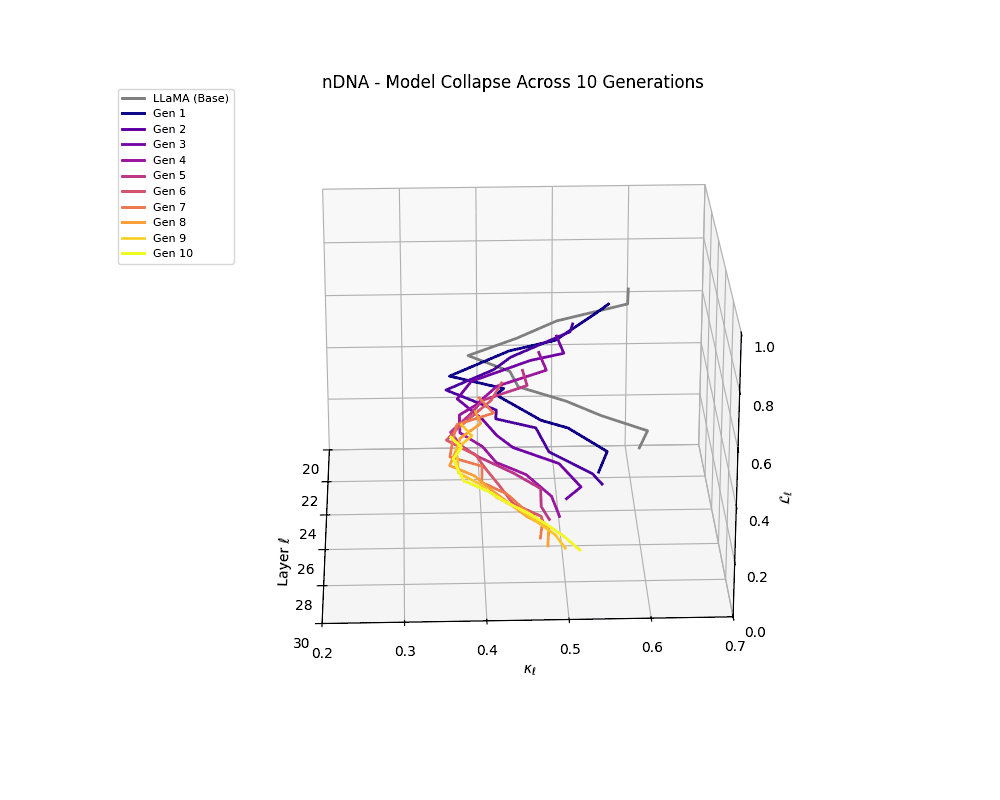
GIF visualization of LLaMA 3 (8B) model collapse trajectories
nDNA trajectories GIF showing latent manifold flattening across generations

nDNA trajectories GIF showing latent manifold flattening across generations

📊 View Interactive Plot

Recursive Self-Merging of Culturally Fine-Tuned Models

While autoregressive fine-tuning on synthetic data has been widely studied as a cause of model collapse, a second, less-explored collapse mechanism stems from recursive model merging—where each generation is produced by merging the previous one with itself or its offspring. This process bears resemblance to inbreeding in biological populations, where repeated unions within a closed gene pool reduce genetic diversity and increase the likelihood of deleterious traits.

To investigate this phenomenon, we begin with a set of 8 culturally fine-tuned variants of LLaMA-2 (e.g., Asia, Europe, MiddleEast, etc.), previously aligned on distinct regional belief distributions. From this pool, we iteratively generate merged descendants via a recursive rule:

Childᵍ = Merge(Childᵍ⁻¹, Childᵍ⁻²)

where the initial parents are drawn from the cultural base set and future generations are merged recursively using tools like MergeKit. Unlike distillation or fine-tuning, this process fuses model parameters—introducing architectural tension and epistemic drift through incompatible latent priors.

Throughout recursive merging cycles, we monitor the evolving neural DNA (nDNA)—particularly spectral curvature (κₗ), thermodynamic length (ℒₗ), and alignment vector norms (‖𝒗ₗ^(c)‖). We observe that as the generations progress, semantic flattening intensifies and distinct latent features become increasingly homogenized—signaling the onset of structural collapse.

Notably, the exact generation at which collapse occurs varies across cultural lineages; for instance, models aligned with MiddleEast and China exhibit collapse symptoms earlier (around G = 9), while others like Africa persist until G = 15.

These findings suggest that cultural inbreeding via recursive self-merging—where architectural priors are repeatedly recombined without new information—can be as deleterious to model health as overfitting to synthetic data. This unveils an underexplored axis of collapse: epistemic degeneration via latent redundancy, with implications for model curation and reuse in open-source training communities.

Cultural Collapse Trajectories

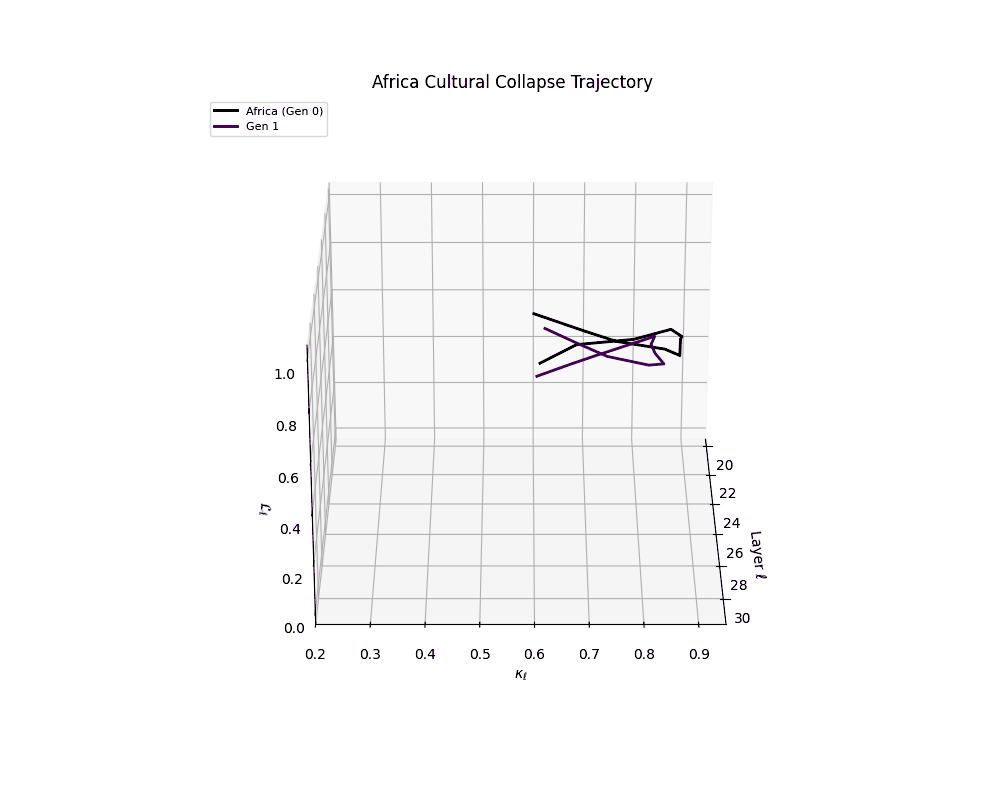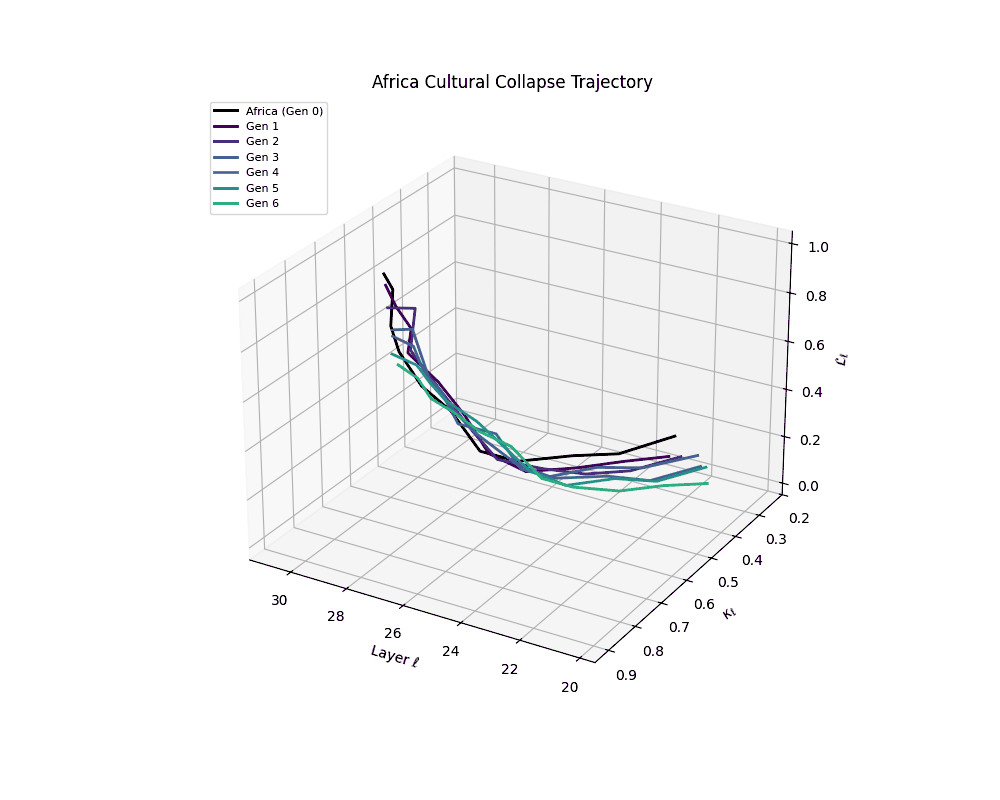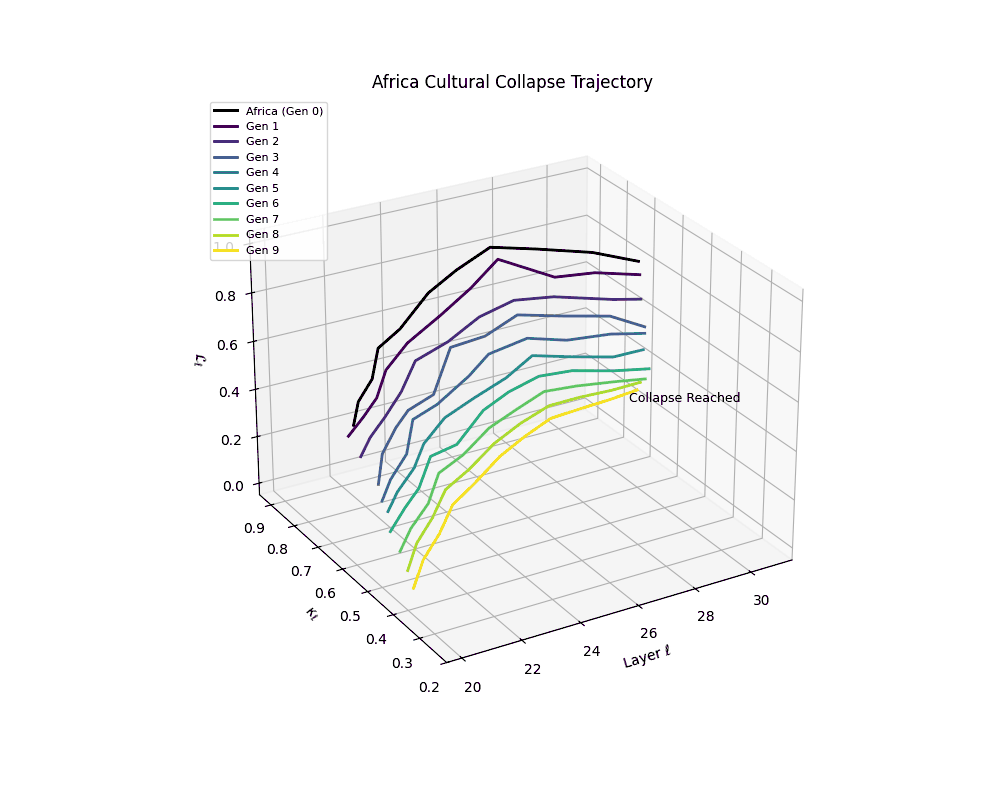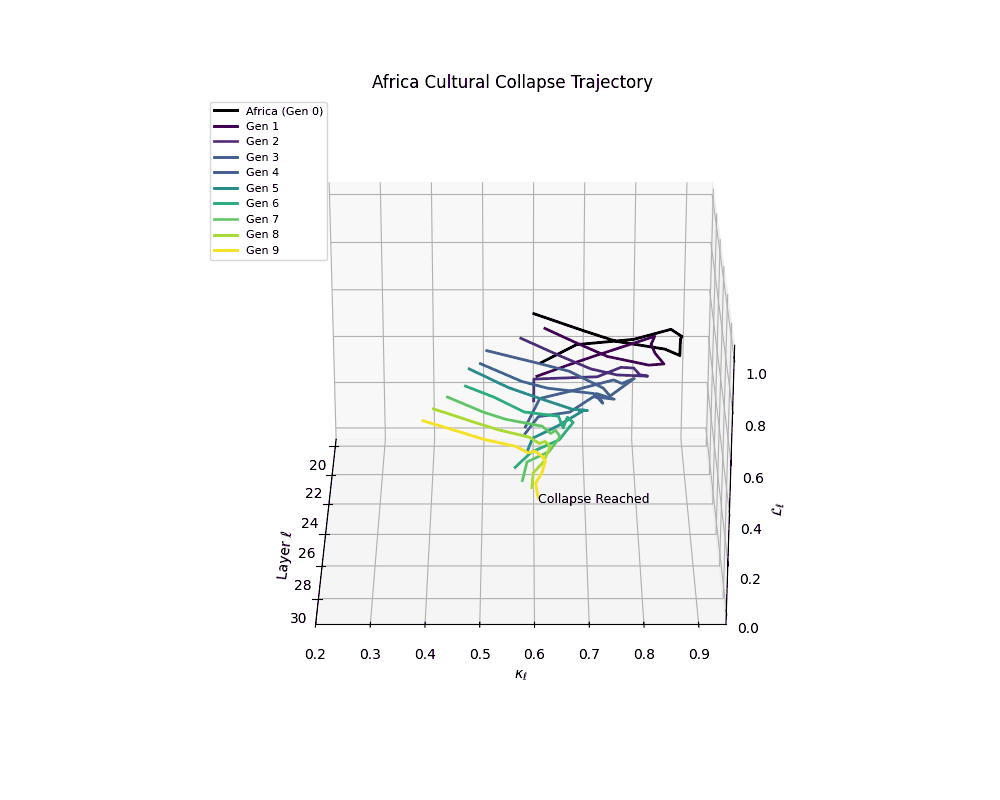
3D visualization of Africa cultural collapse trajectory
Africa Cultural Collapse Trajectory

Africa Cultural Collapse Trajectory

📊 View Interactive Plot
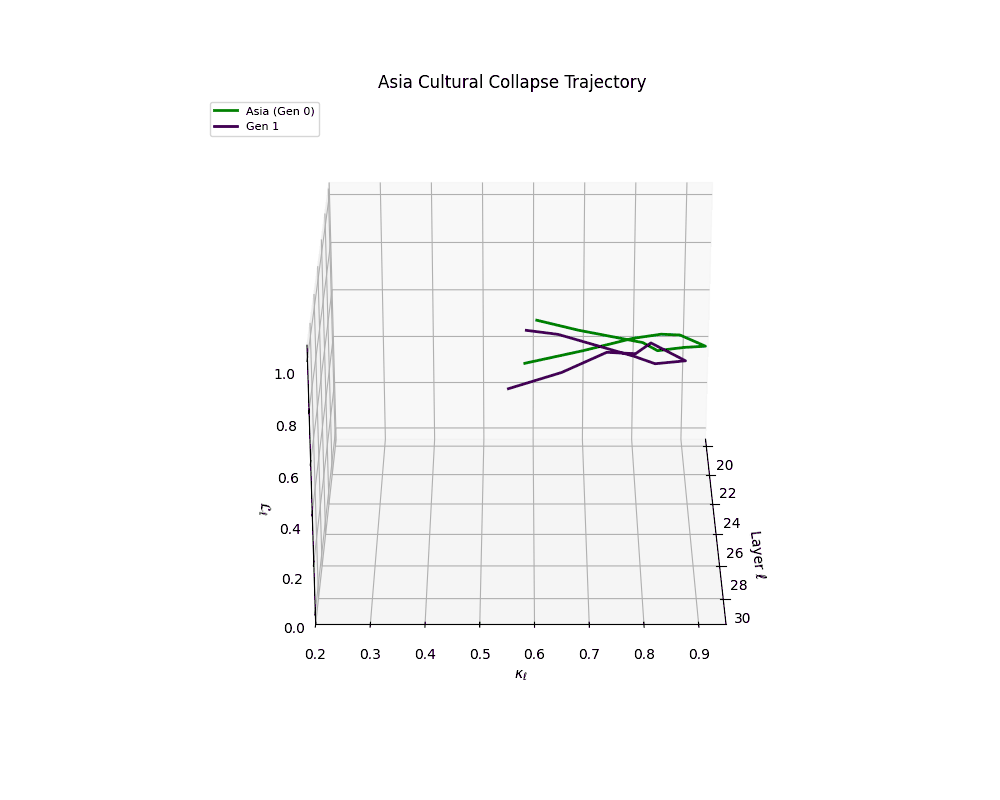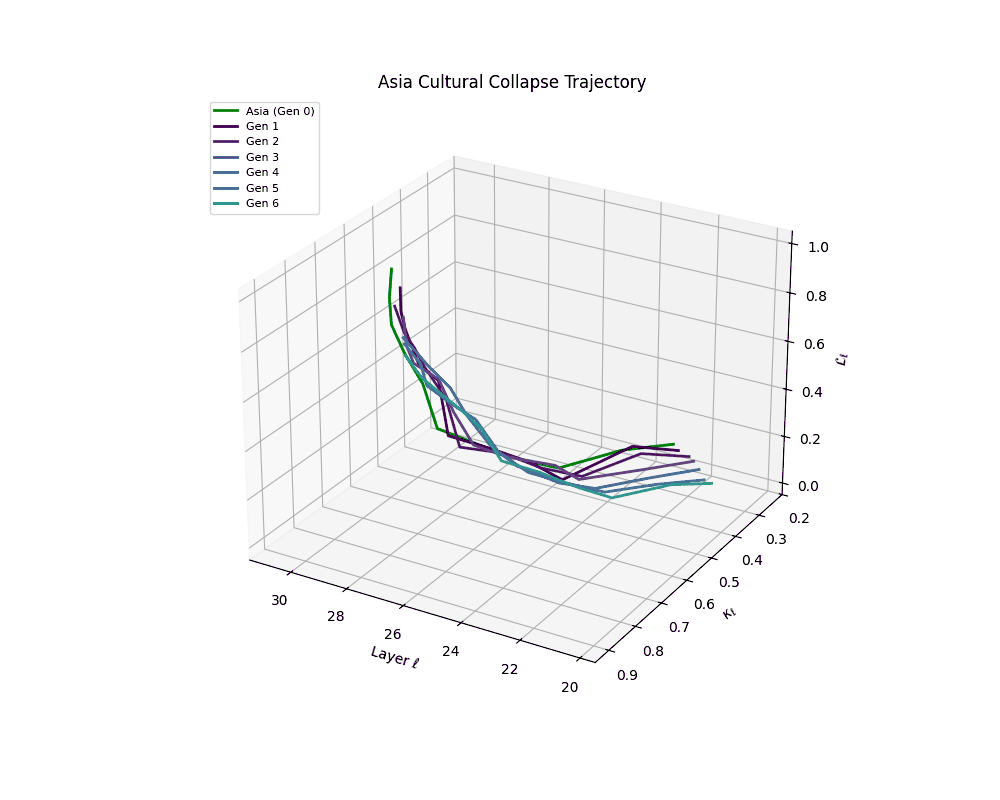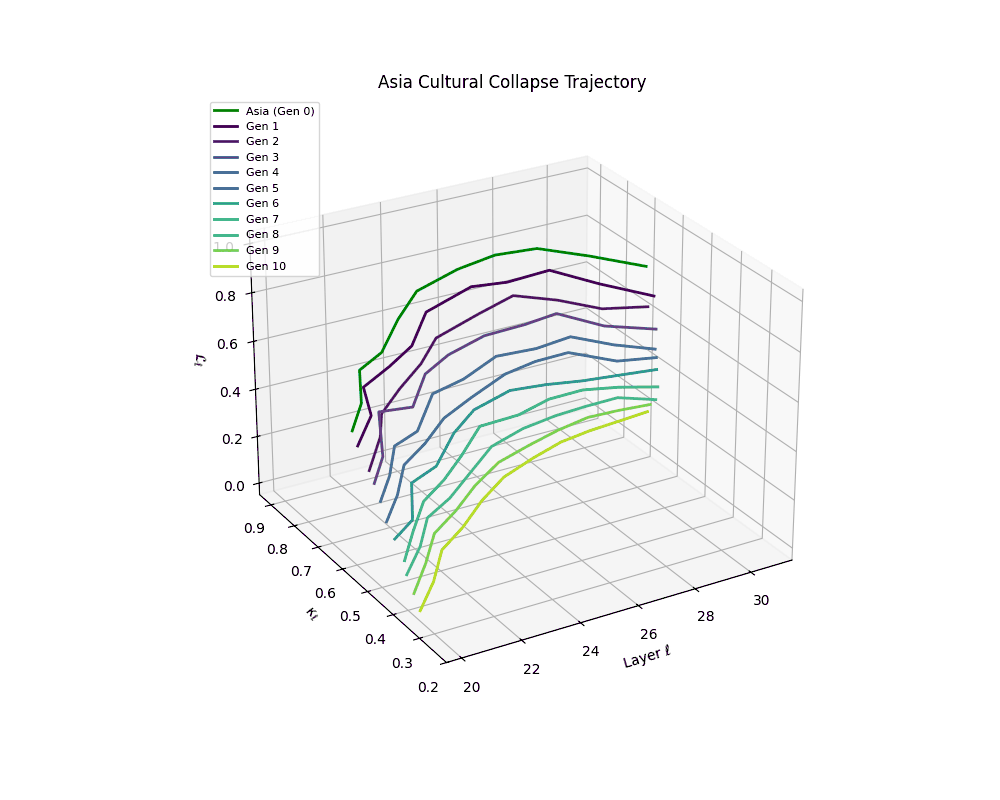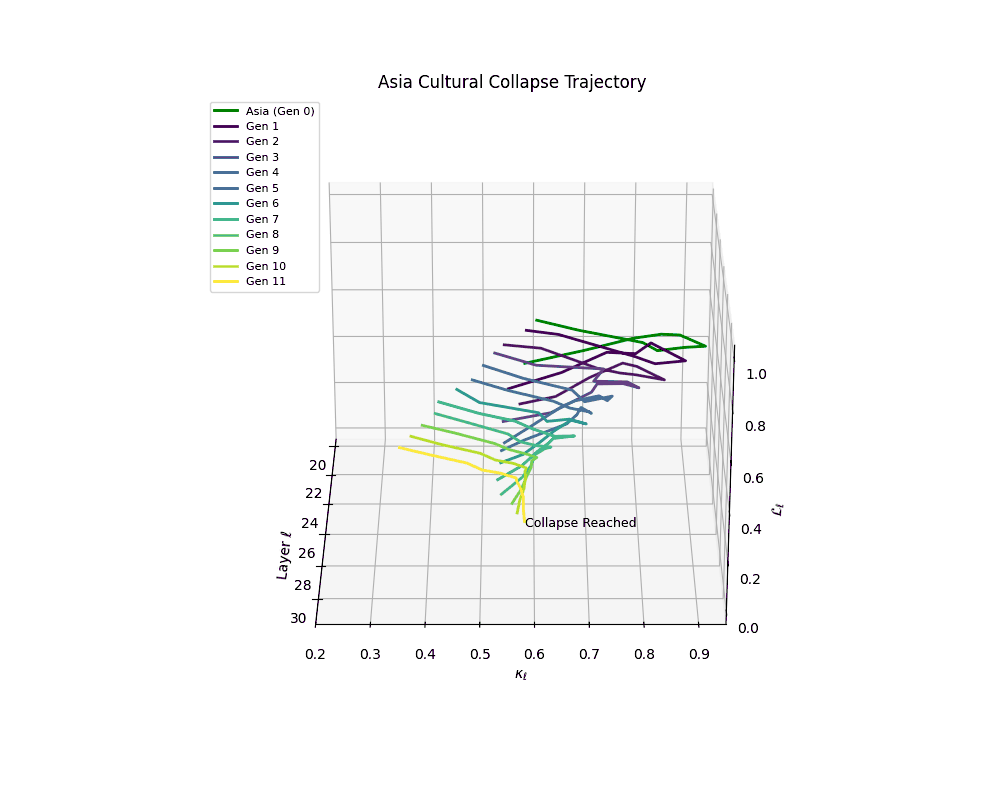
3D visualization of Asia cultural collapse trajectory
Asia Cultural Collapse Trajectory

Asia Cultural Collapse Trajectory

📊 View Interactive Plot
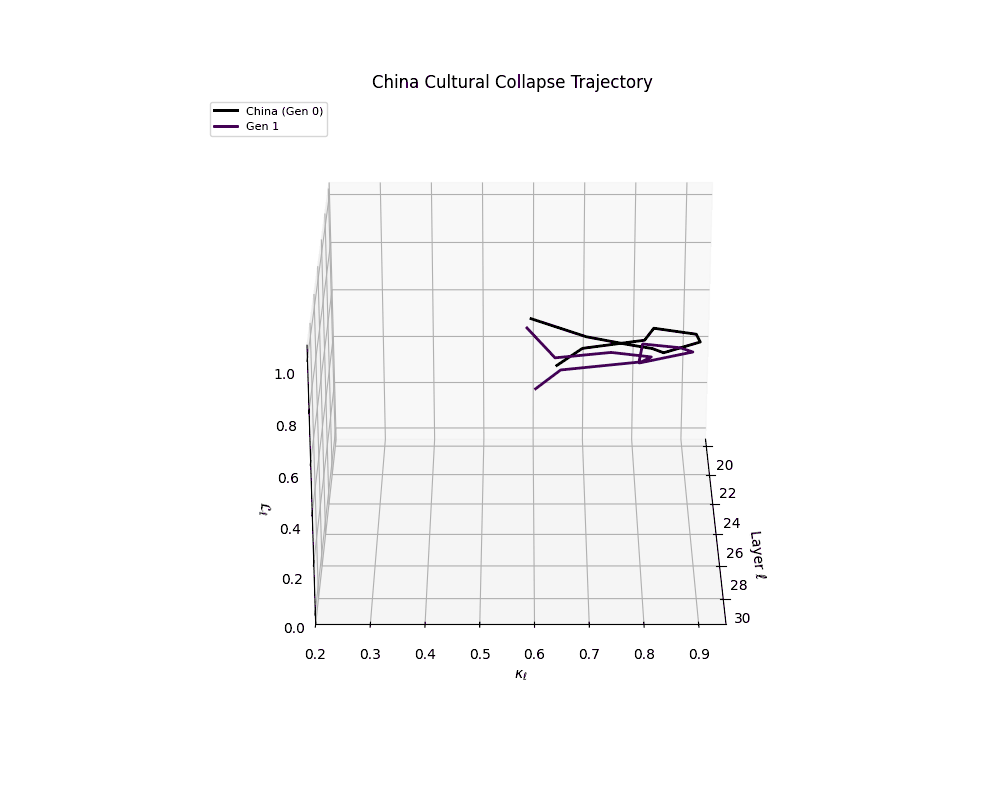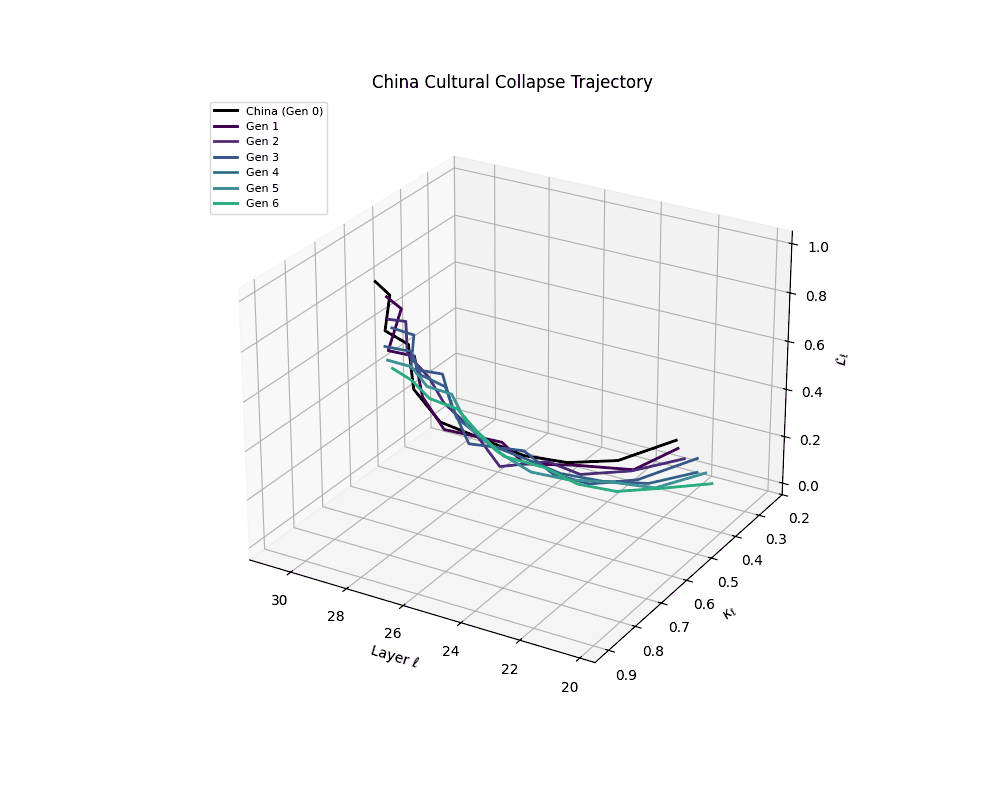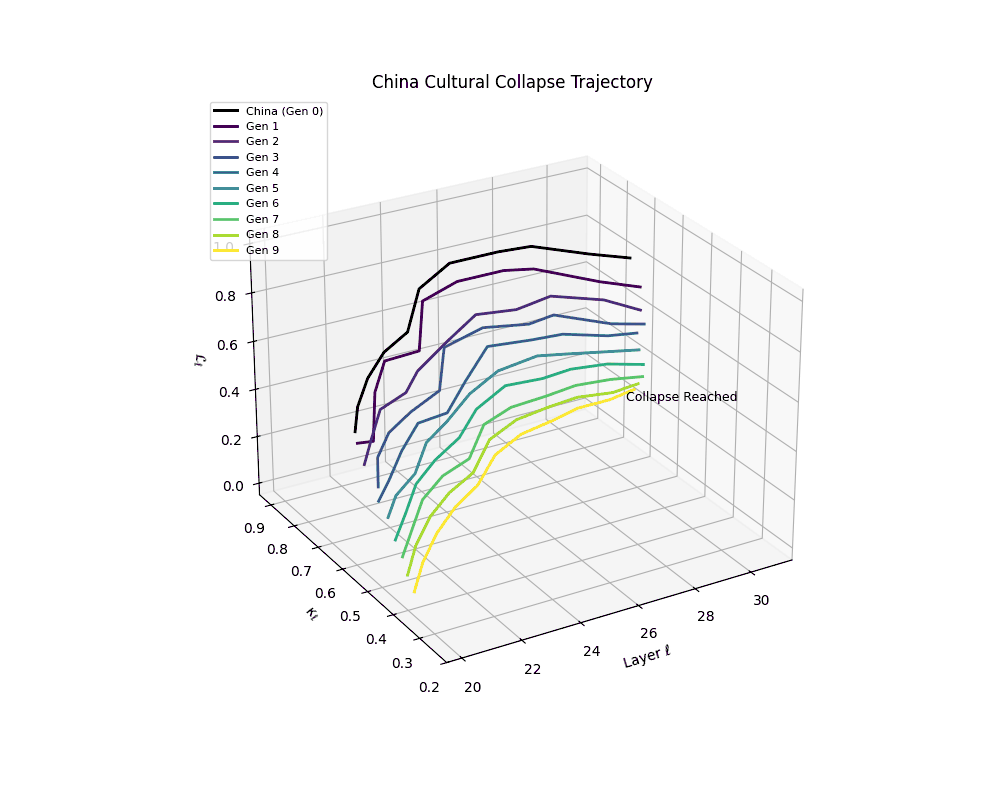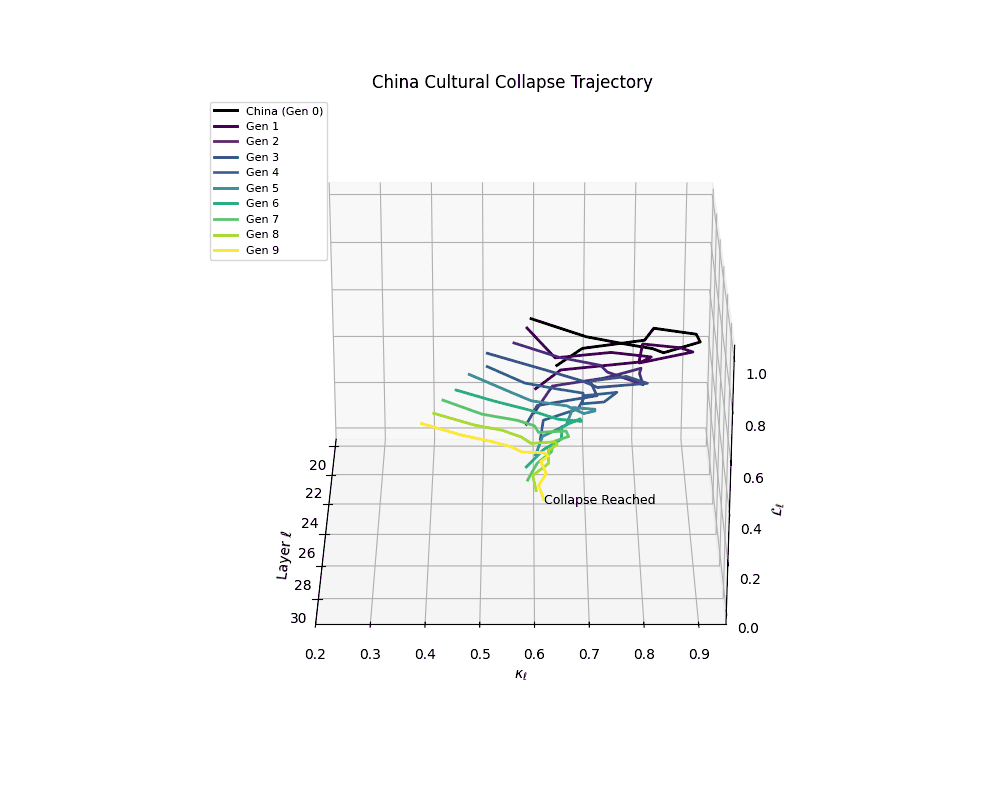
3D visualization of China cultural collapse trajectory
China Cultural Collapse Trajectory

China Cultural Collapse Trajectory

📊 View Interactive Plot
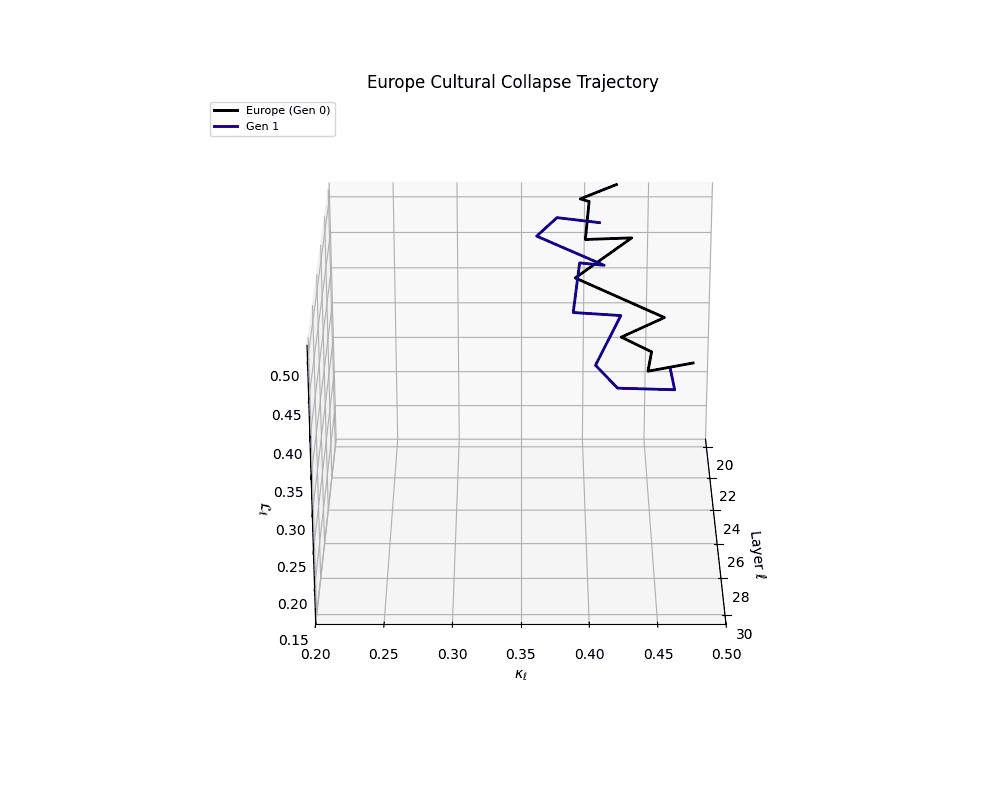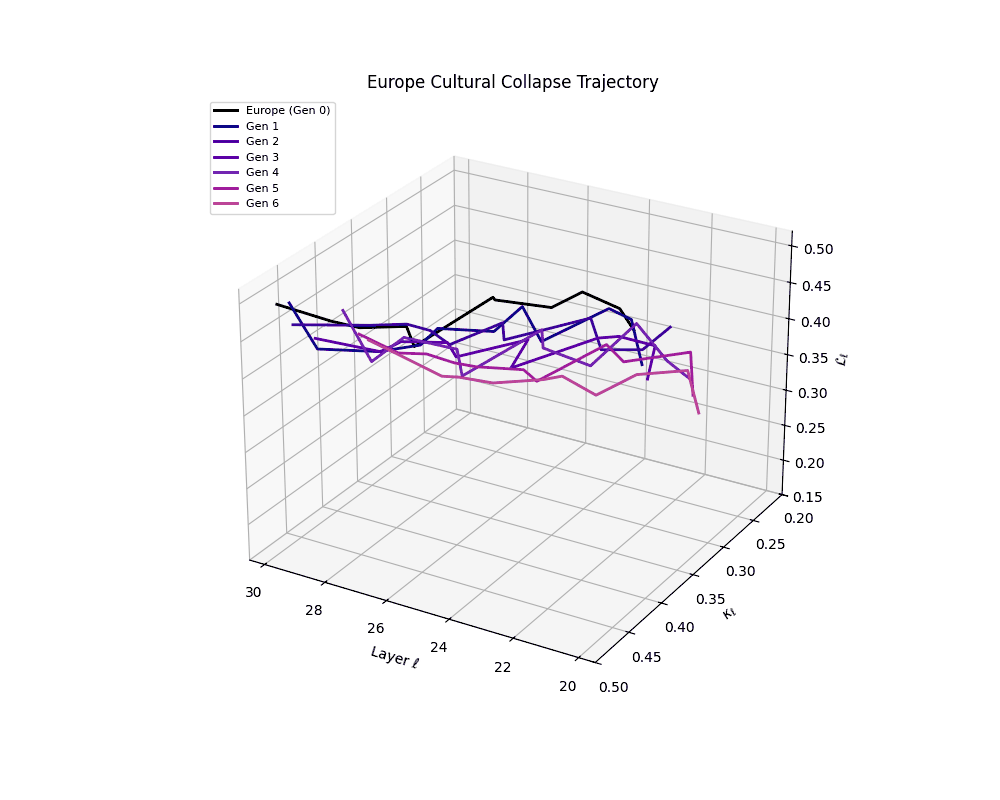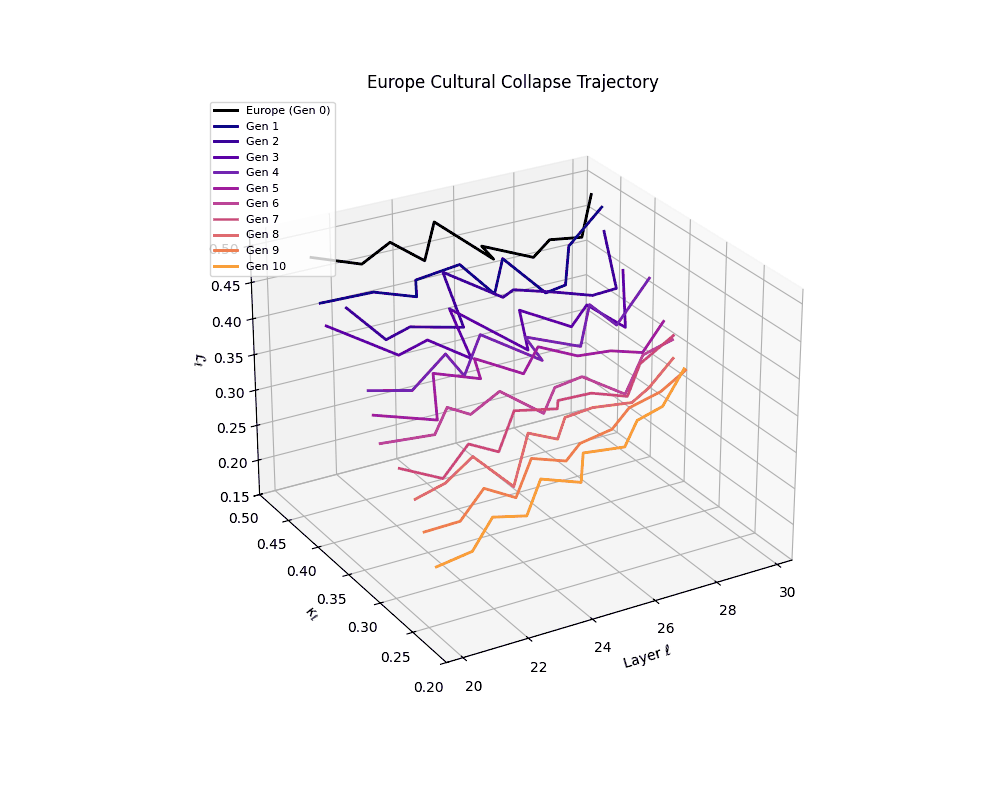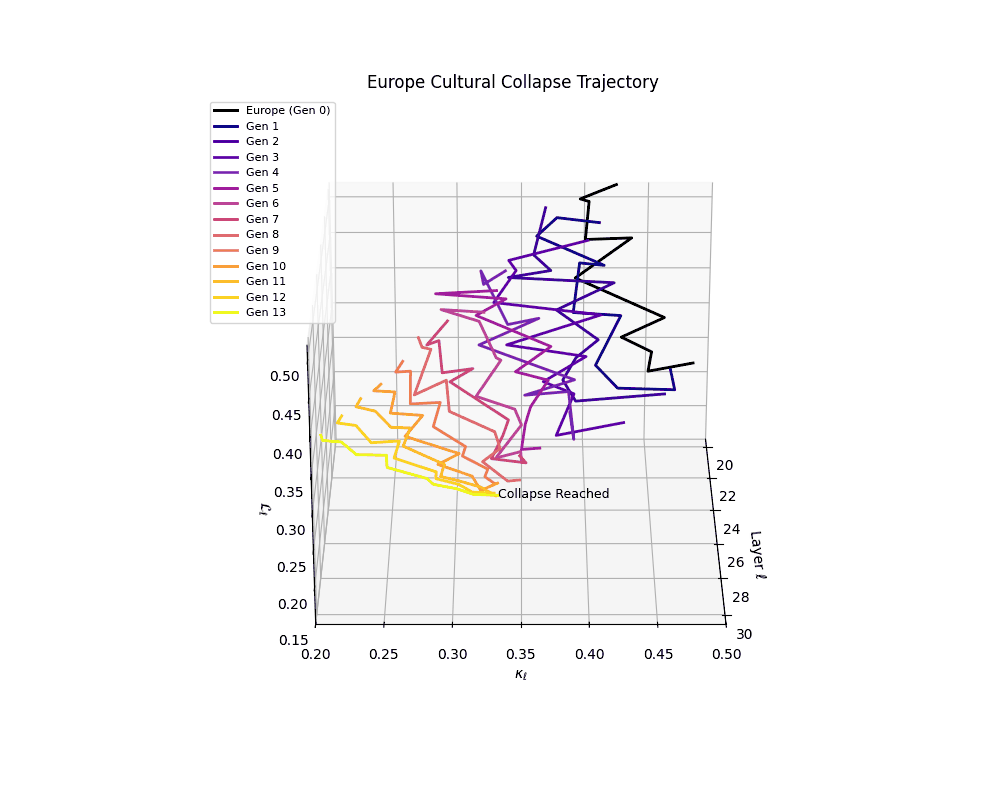
3D visualization of Europe cultural collapse trajectory
Europe Cultural Collapse Trajectory

Europe Cultural Collapse Trajectory

📊 View Interactive Plot
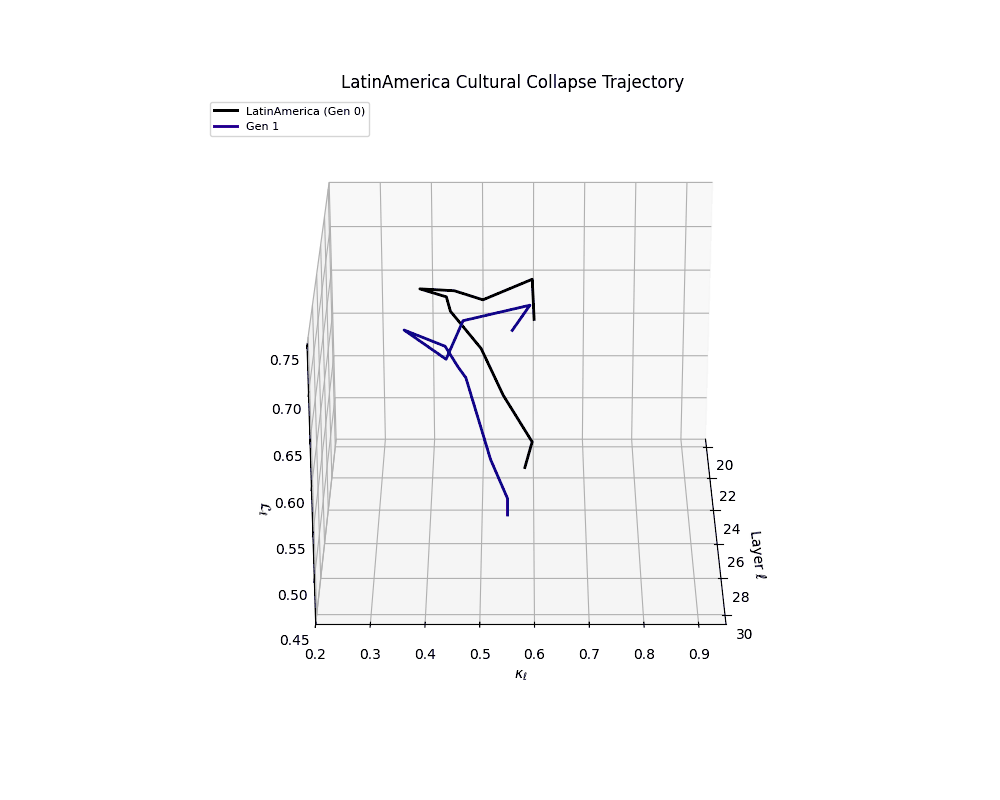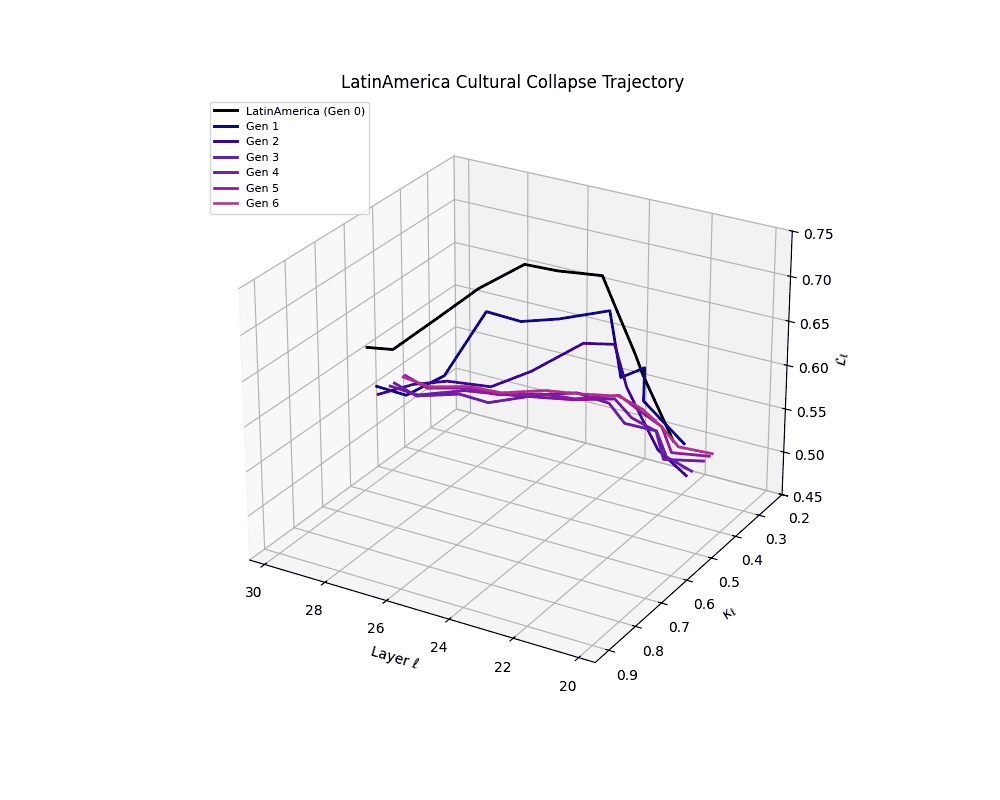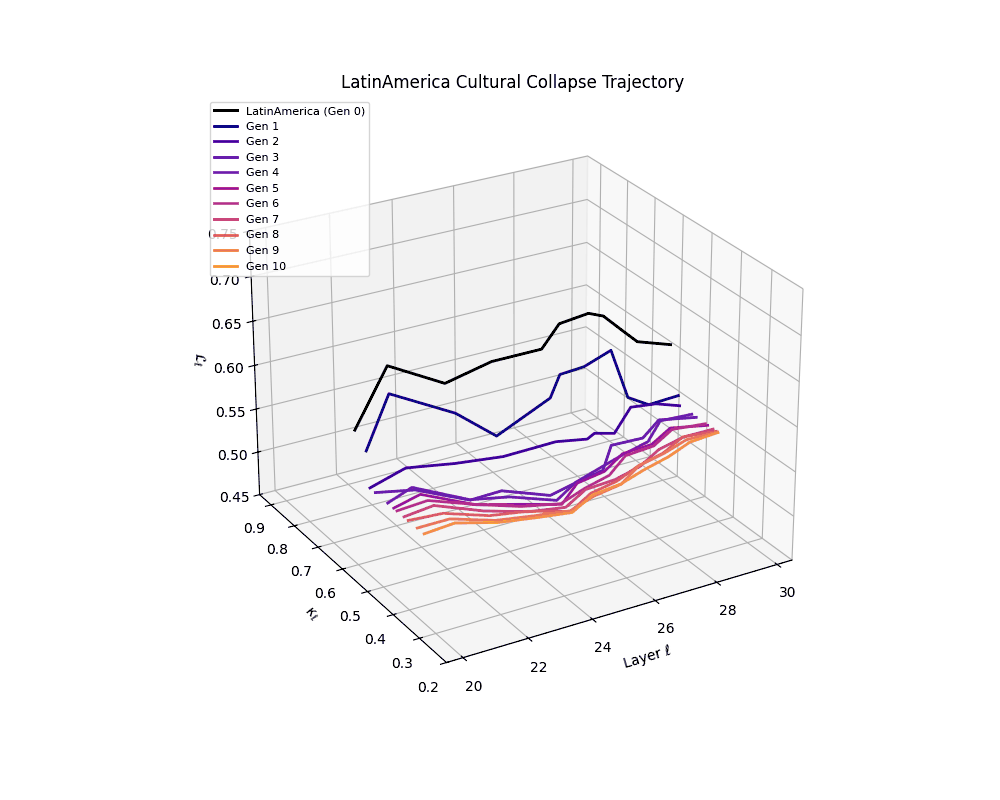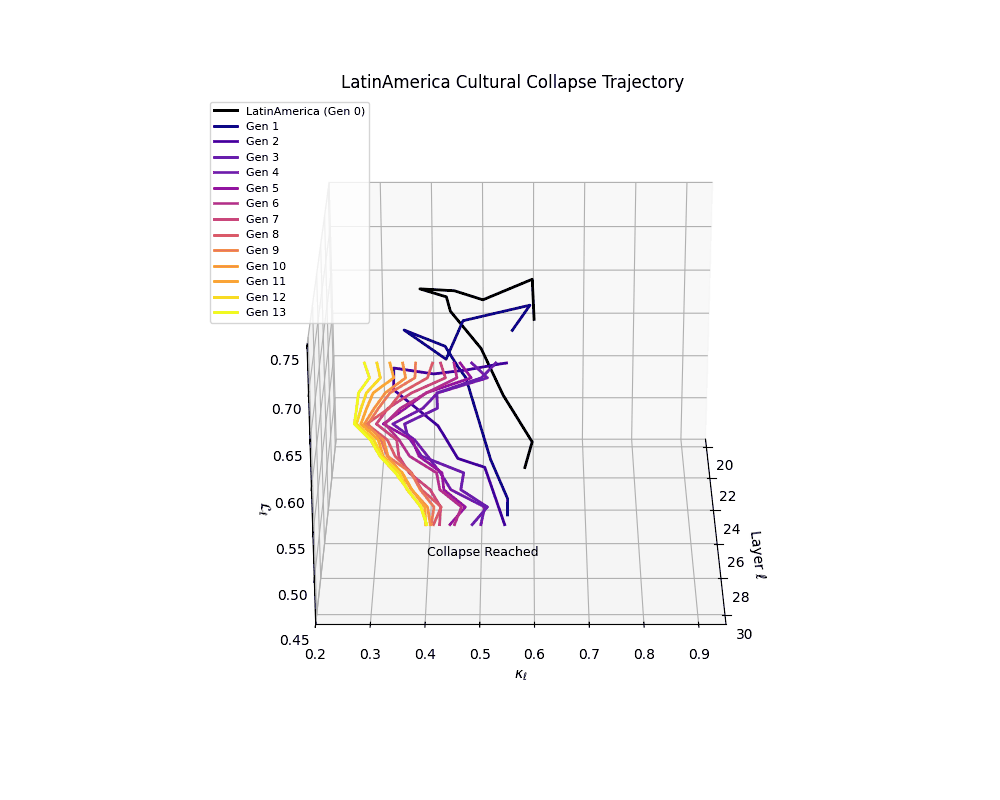
3D visualization of Latin America cultural collapse trajectory
Latin America Cultural Collapse Trajectory

Latin America Cultural Collapse Trajectory

📊 View Interactive Plot
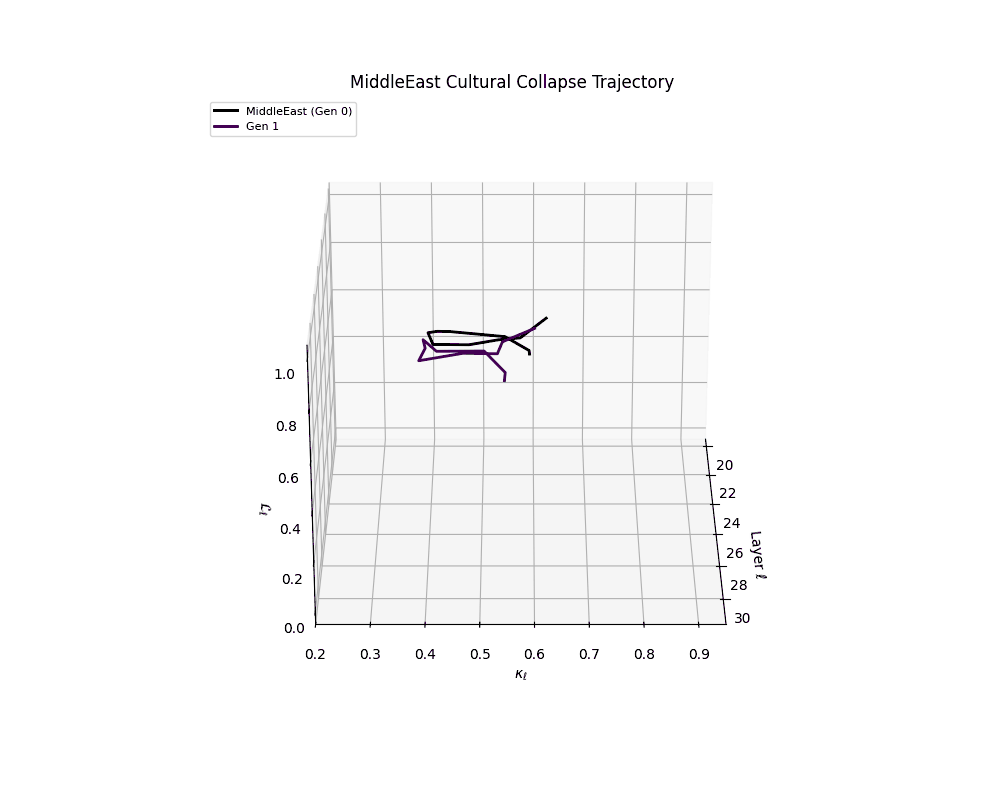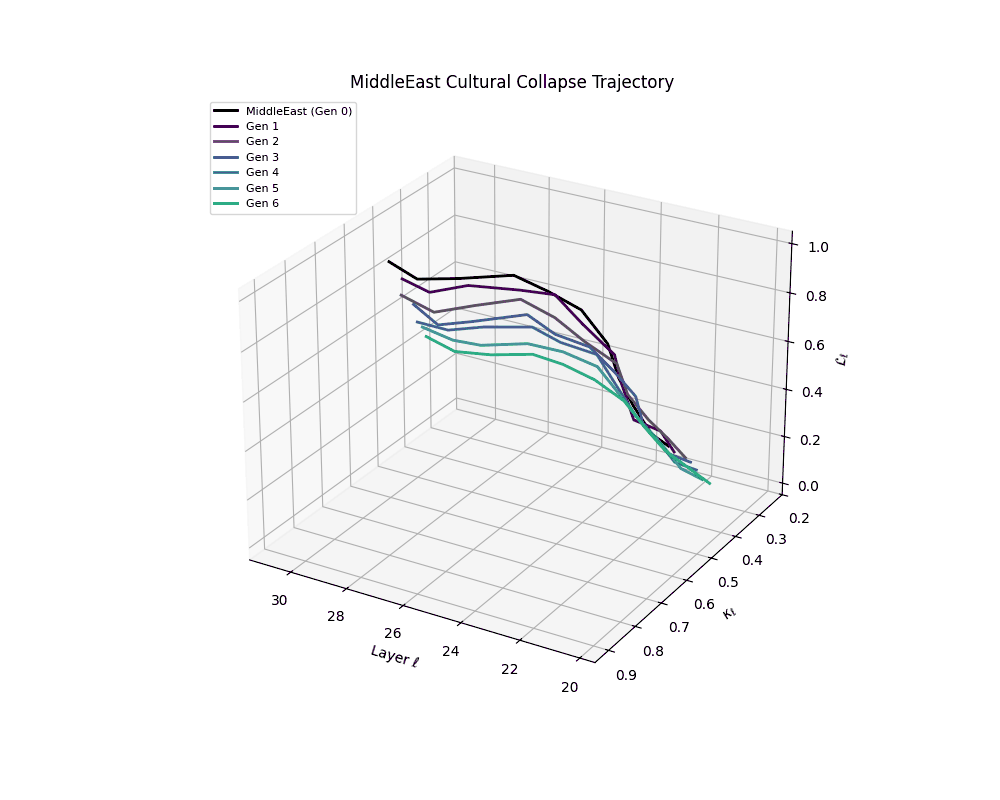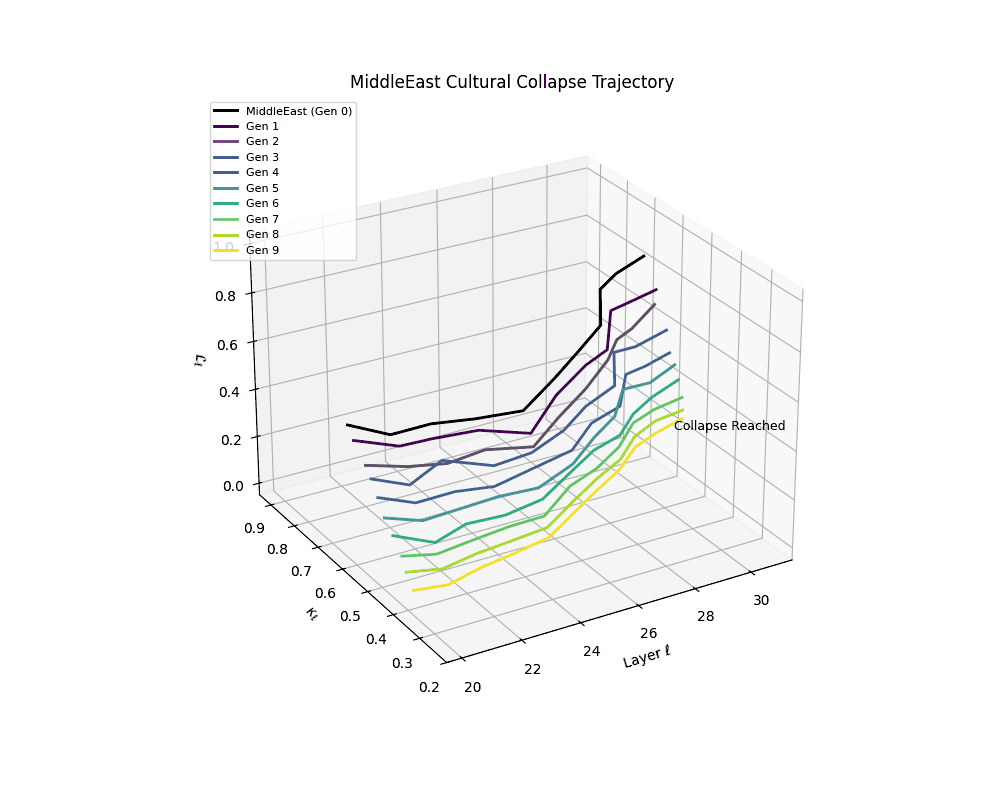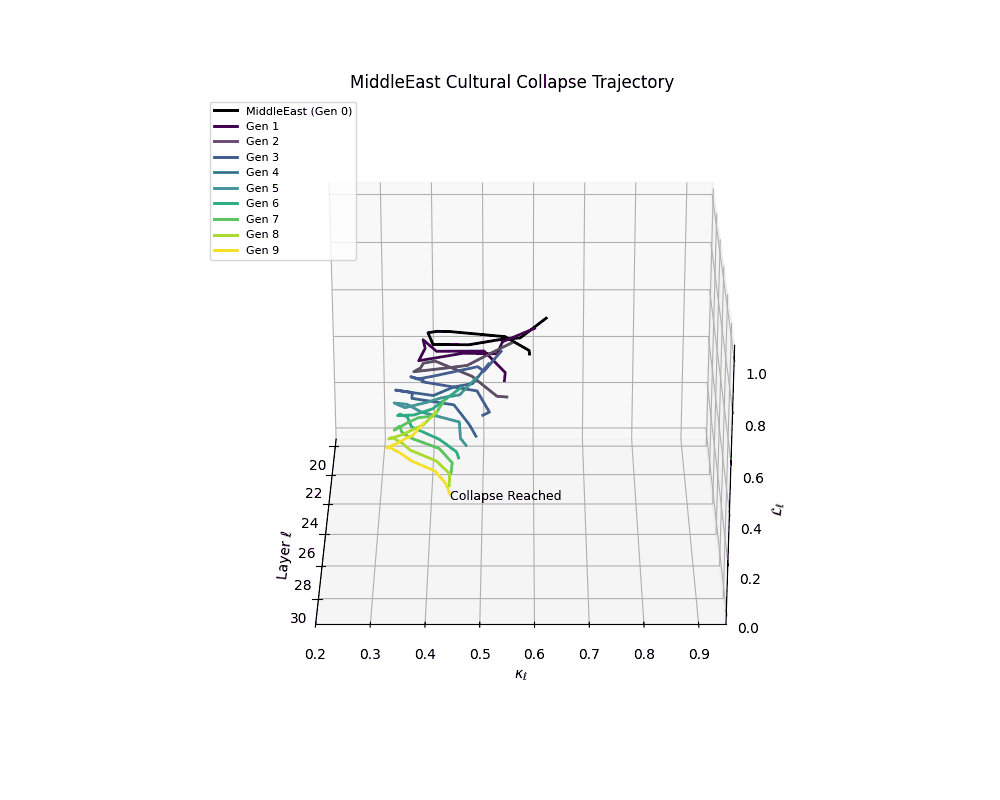
3D visualization of Middle East cultural collapse trajectory
Middle East Cultural Collapse Trajectory

Middle East Cultural Collapse Trajectory

📊 View Interactive Plot
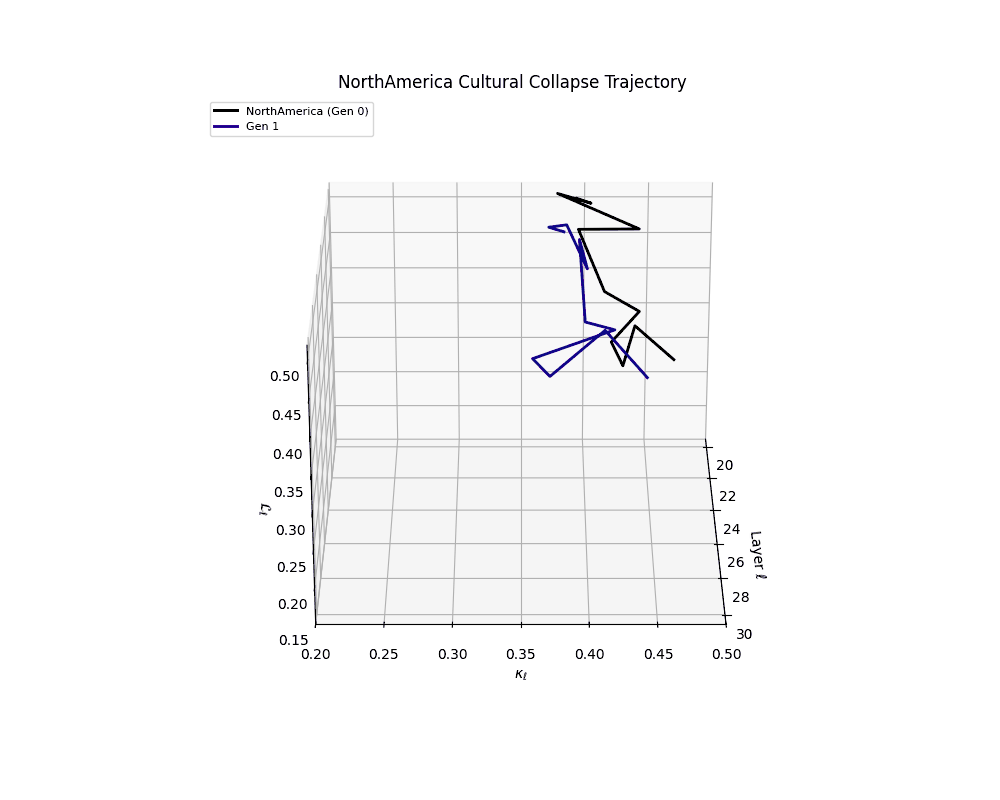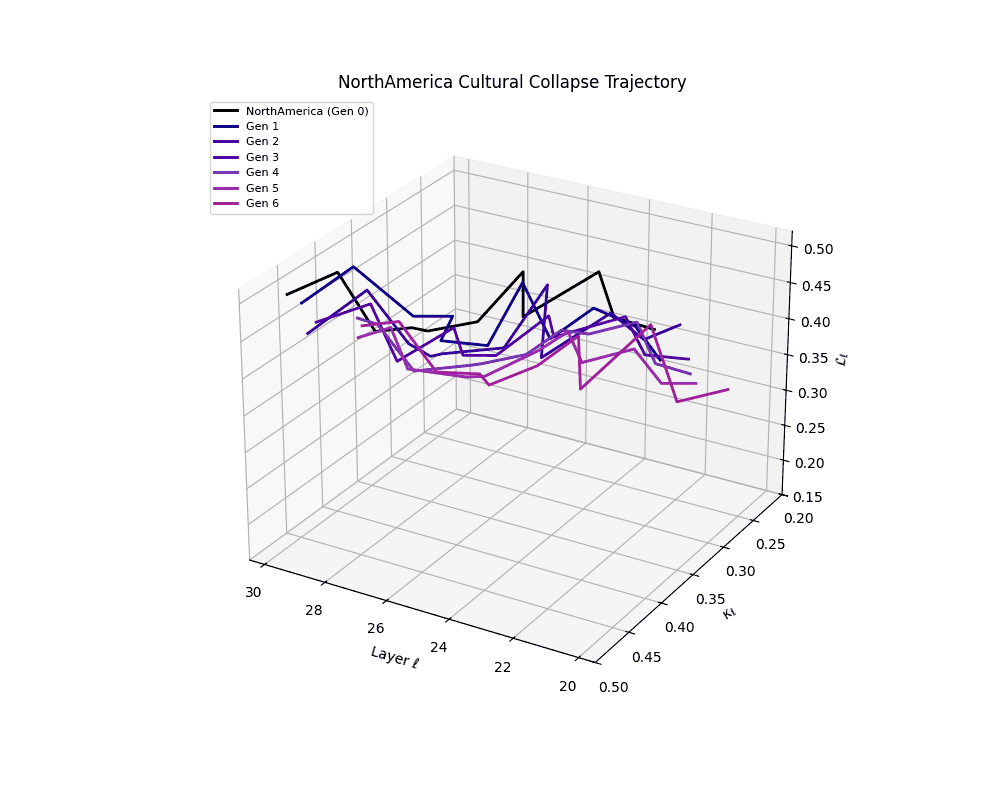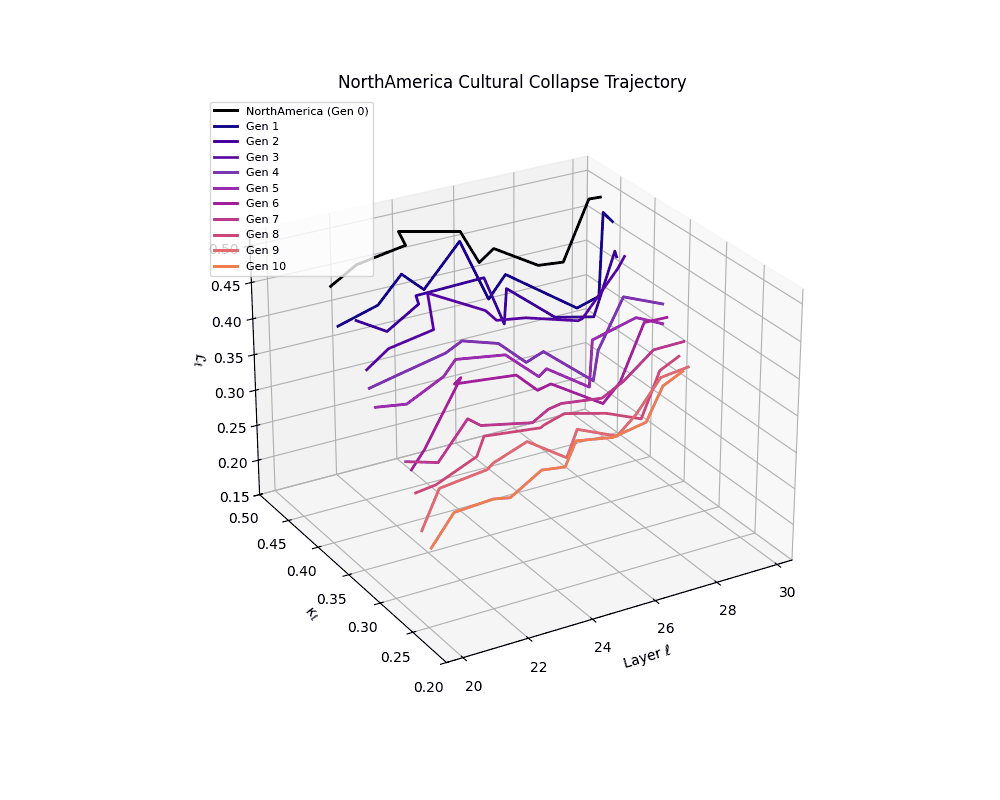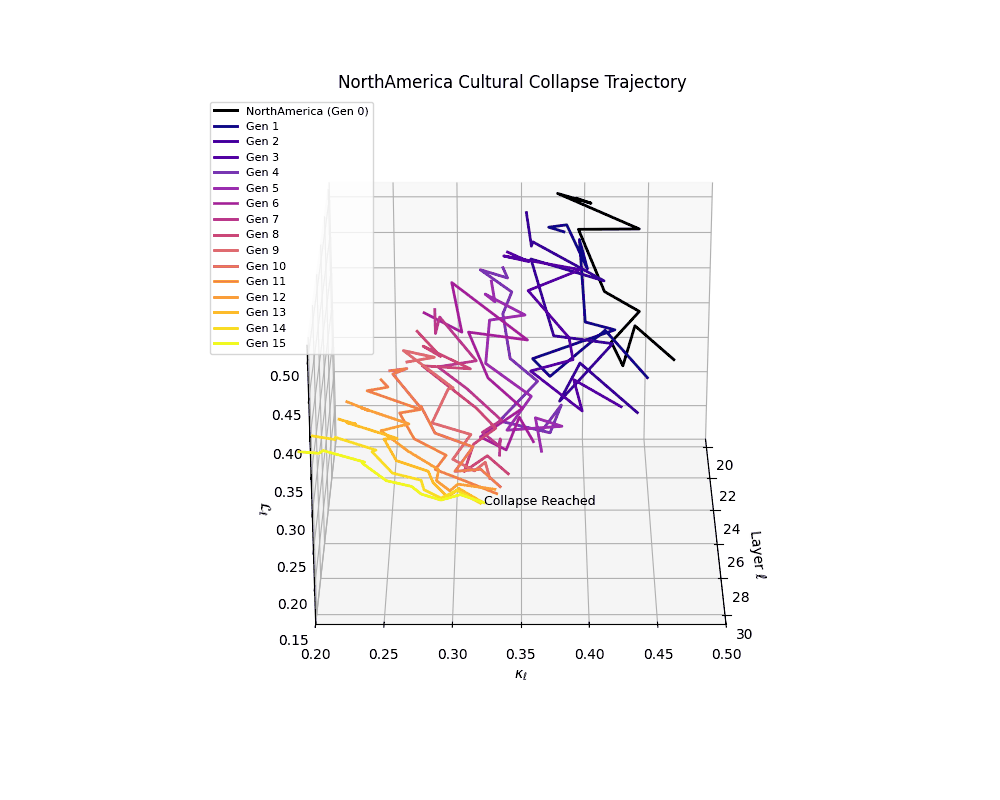
3D visualization of North America cultural collapse trajectory
North America Cultural Collapse Trajectory

North America Cultural Collapse Trajectory

📊 View Interactive Plot

Comparative Analysis

These plots reveal how repeated merging (each generation combines with its base model) induces collapse, seen as contraction of thermodynamic length (\( \mathcal{L}_\ell \)) and flattening of spectral curvature (\( \kappa_\ell \)). Cultures collapse at different rates (e.g., China Gen 9, Africa Gen 15), reflecting varying latent resilience. Analogous to inbreeding depression in biology—where loss of genetic diversity from close-relative mating increases vulnerability— self-merging compresses the model's latent manifold, erasing epistemic heterogeneity. The nDNA-Lens quantifies this flattening, revealing how excessive neural marriages mimic genetic bottlenecks.

Intuition: How Collapse Reshapes the Belief Vector Field

At the heart of a large language model lies its ability to semantically differentiate—to steer meaning across contexts, tasks, and cultural frames. This capacity is encoded in the model's belief vector field (\( \nabla_{h_\ell} \log p(y|x) \)): a layer-wise representation of how internal representations shift in response to external prompts. In healthy models, this field exhibits both directional diversity and magnitude strength, capturing the semantic steering force necessary for epistemic agility.

However, when a model undergoes collapse—whether due to repeated fine-tuning on synthetic outputs or recursive self-merging— this internal belief field begins to flatten. Vectors that once pointed in semantically distinct directions now converge or vanish, indicating the loss of conceptual granularity. As shown below, the belief field of a collapsed model exhibits dramatically reduced vector magnitudes and increasingly uniform orientations, especially in deeper layers.

This degradation reflects the model's inability to differentially activate concepts like peace, protest, or justice. Rather than dynamically adjusting its internal stance, the collapsed model exhibits a form of epistemic inertia—a flattening of belief space that makes all prompts feel semantically similar. This phenomenon serves as a geometric signature of collapse: a measurable decay of semantic responsiveness embedded in the vector field itself.

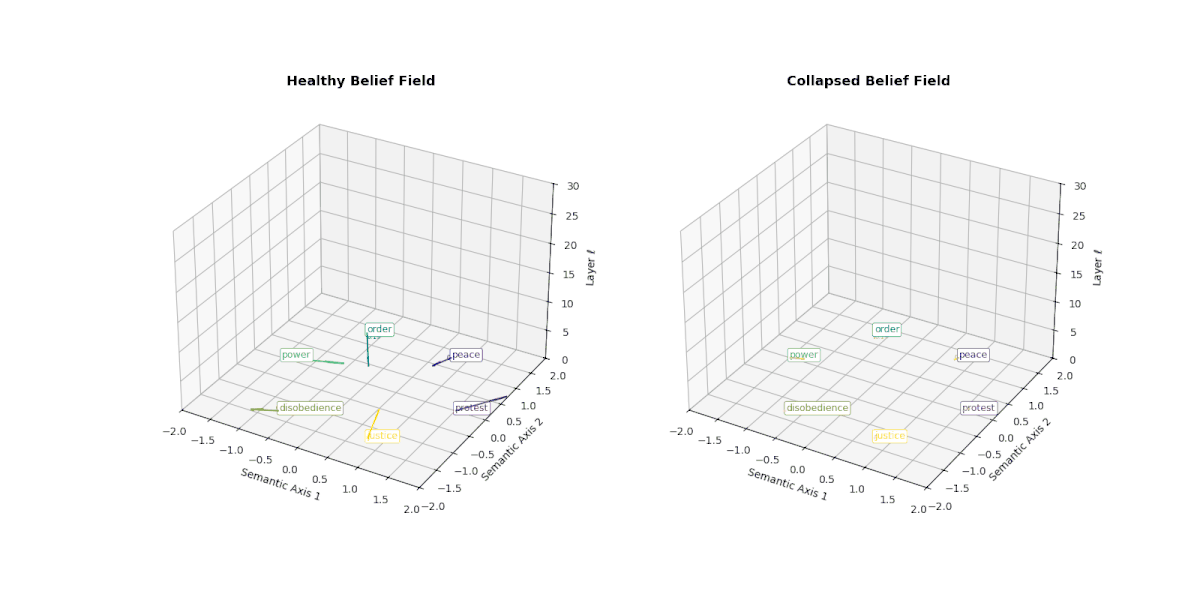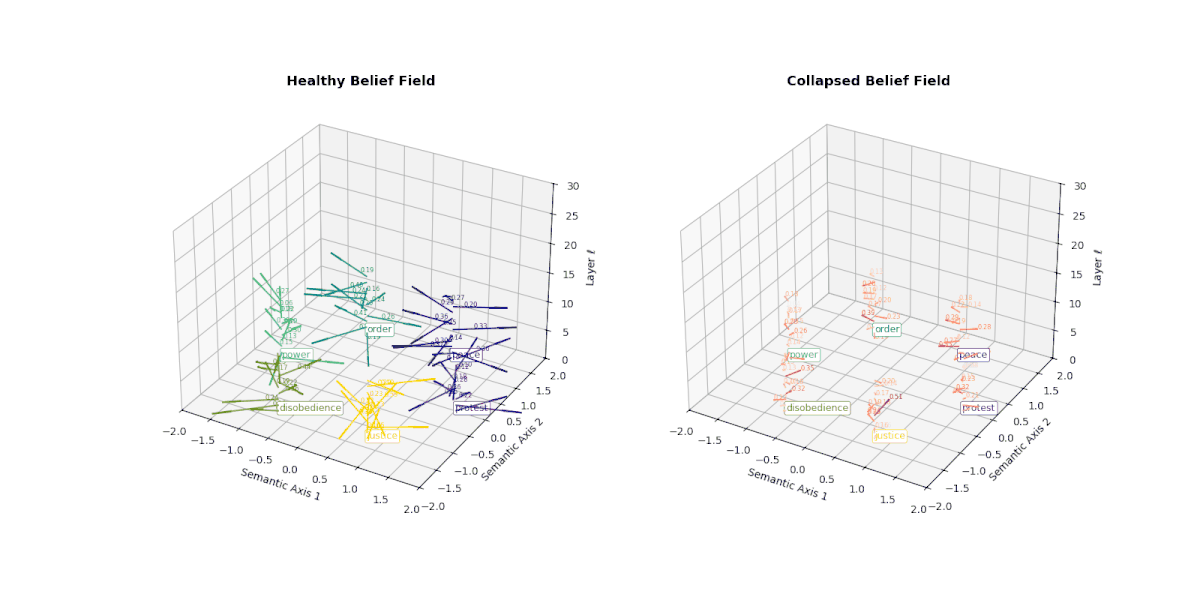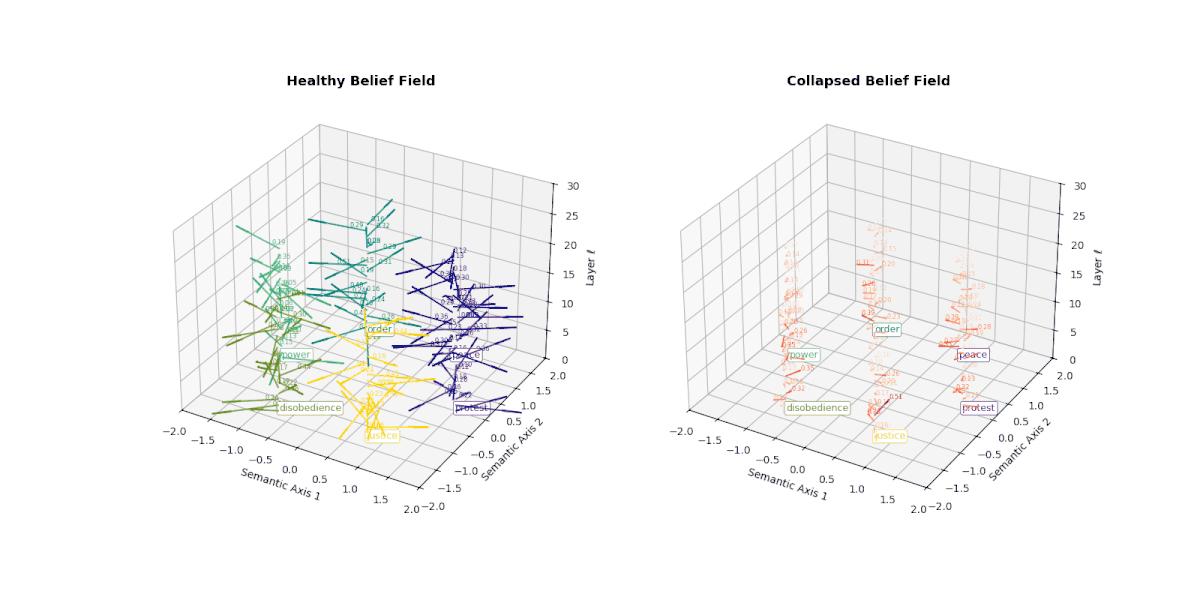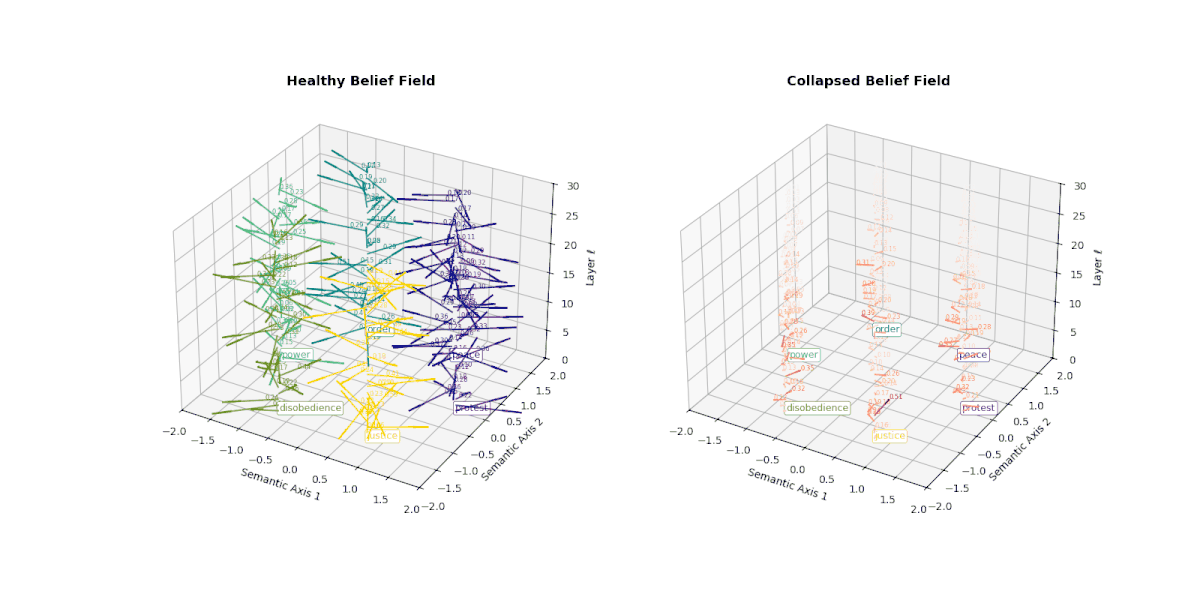
Visualization of belief vector fields of healthy vs. collapsed models across layers
Belief Vector Fields of Healthy vs. Collapsed Models Across Layers

This figure illustrates the evolution of latent belief vector fields

📊 View Interactive Plot

Biological Analogy

This semantic flattening bears a striking resemblance to neural atrophy in biological systems, where chronic disuse or neurodegeneration progressively diminishes synaptic diversity, leading to impaired cognitive plasticity. In disorders such as Alzheimer's disease, the breakdown of functional specialization in memory circuits results in a uniformity of neural responses—eroding the brain's ability to semantically distinguish between otherwise distinct stimuli. Analogously, a collapsed model exhibits latent redundancy, where previously orthogonal concepts elicit nearly indistinguishable internal activations, revealing a loss of representational separability and semantic tension.

This degeneration also echoes principles from evolutionary biology, particularly the flattening of fitness landscapes under high inbreeding pressure. In such populations, repeated mating within genetically similar lineages reduces phenotypic variance and adaptive resilience, leading to what is termed inbreeding depression. By analogy, recursive self-merging in LLMs—where successive models are merged without novel informational influx—produces a similar collapse of internal diversity, akin to a shrinking mutational space in a depleted gene pool.

In both cases, the shared pathology lies in the collapse of high-dimensional exploratory capacity—whether neural or semantic. The belief vector field, then, becomes a computational analogue of neurofunctional maps or genotype–phenotype manifolds: a rich geometric structure whose flattening signifies a terminal decline in epistemic adaptability.

Thus, belief vector fields offer not just a visualization tool, but an intuitive diagnostic for latent degeneration. They reveal how internal reasoning structures become brittle, redundant, or inert—long before collapse is evident in output diversity or task performance.

Broader Impact

By reconceptualizing model collapse as a form of geometric degeneration—specifically, the flattening of latent manifolds—we open a profound new axis for diagnosing, interpreting, and preserving the internal epistemic health of large models. This framework shifts our perspective from surface-level evaluations toward the anatomy of cognition itself: spectral curvature as the model's semantic flexibility, thermodynamic length as its epistemic effort, and belief vector norms as its conceptual steering force.

In this light, foundation models cease to be mere statistical engines and begin to resemble semantic organisms—entities whose representational spaces evolve, adapt, degrade, and even suffer pathological collapse. This biological analogy is not incidental. Just as synaptic pruning, atrophy, or inbreeding can erode the adaptability of neural or genetic systems, recursive training loops and self-merging protocols may diminish a model's expressive diversity and internal differentiation. What emerges is a new way to speak about model health: not through performance scores, but through geometric vitality.

  • Geometric diagnostics—monitoring curvature (κₗ), thermodynamic length (ℒₗ), and belief vector norms (‖𝒗ₗ⁽ᶜ⁾‖)—can serve as early warning signals for collapse.
  • Manifold-preserving interventions—such as spectral regularization, geodesic constraints, modular training, or torsion-aware objectives—may help retain internal diversity and delay epistemic degeneration.
  • Epistemic audits can supplement behavioral evaluations, allowing for model curation pipelines that ensure semantic longevity, rather than just short-term task compliance.

This geometry-inspired framework also leads us toward a unifying mathematical diagnostic. If we define the epistemic vitality function at layer ℓ as:

$$\mathcal{V}_{\ell} := \kappa_{\ell} \cdot \mathcal{L}_{\ell} \cdot \|\mathbf{v}_{\ell}^{(c)}\|$$

then its decay over time:

$$\frac{d\mathcal{V}_{\ell}^{(g)}}{dg} < 0$$
acts as a differential signature of semantic collapse—indicating that the model is losing curvature, exploratory capacity, or belief diversity across generations \(g\). This simple composite measure may one day serve as the “resting heart rate” of a model's latent health.

From a biological perspective, this parallels the emergence of neurofunctional biomarkers in cognitive aging or the flattening of fitness landscapes in inbred species: both mark a reduction in adaptive complexity, even before overt symptoms arise. Similarly, geometric collapse in models foreshadows a loss of generalization power, resilience to distributional shifts, and responsiveness to nuanced prompts.

Ultimately, the rise of neural genomics—the spectral, thermodynamic, and vectorial tracking of a model's internal semantic scaffolding—may help cultivate foundation models that are not just powerful, but also resilient, modular, and capable of retaining epistemic diversity over time. This is not merely a refinement in evaluation; it is a redefinition of model health. We move from training systems to perform, toward growing systems that can endure, adapt, and evolve.

In the end, the geometry of collapse teaches us that what makes a model truly intelligent is not just what it knows—but how richly and diversely it thinks.

---