nDNA Logo
LLM
MFM T2I Diffusion LM EFM
nDNA v2
Series
nDNA Book Cover
arXiv GitHub YouTube Cite

nDNA - the Semantic Helix of Artificial Cognition

nDNA - the Semantic Helix of Artificial Cognition

BibTex

@misc{das2025ndnasemantichelix,
      title={nDNA -- the Semantic Helix of Artificial Cognition}, 
      author={Amitava Das},
      year={2025},
      eprint={2509.18216},
      archivePrefix={arXiv},
      primaryClass={cs.AI},
      url={https://arxiv.org/abs/2509.18216}, 
}

ThenDNA -- Cartography Across 15 Foundation Models

To chart the latent genomic landscape of modern foundation models, we choose a representative suite of large language models (LLMs) spanning diverse architectural paradigms, parameter scales, training objectives, and alignment methodologies. Our selection includes:

  • Dense transformers (e.g., LLaMA-2 [1], LLaMA-3 [2], Gemma [3], Falcon [3], GPT-NeoX [4])
  • Sparse mixture-of-expert designs (e.g., Mixtral expert variants [3])
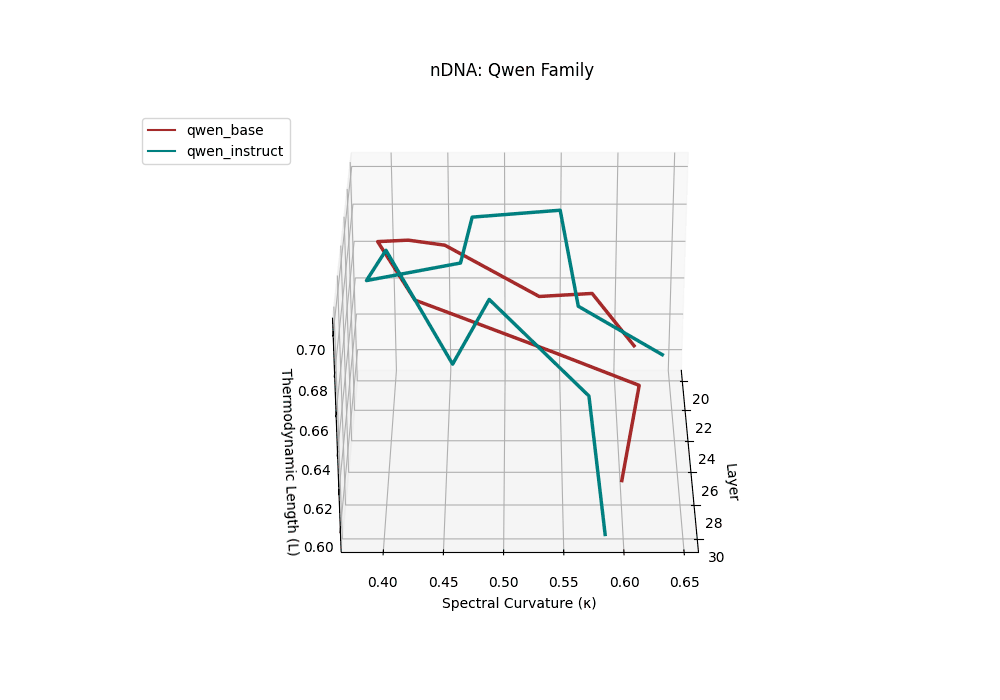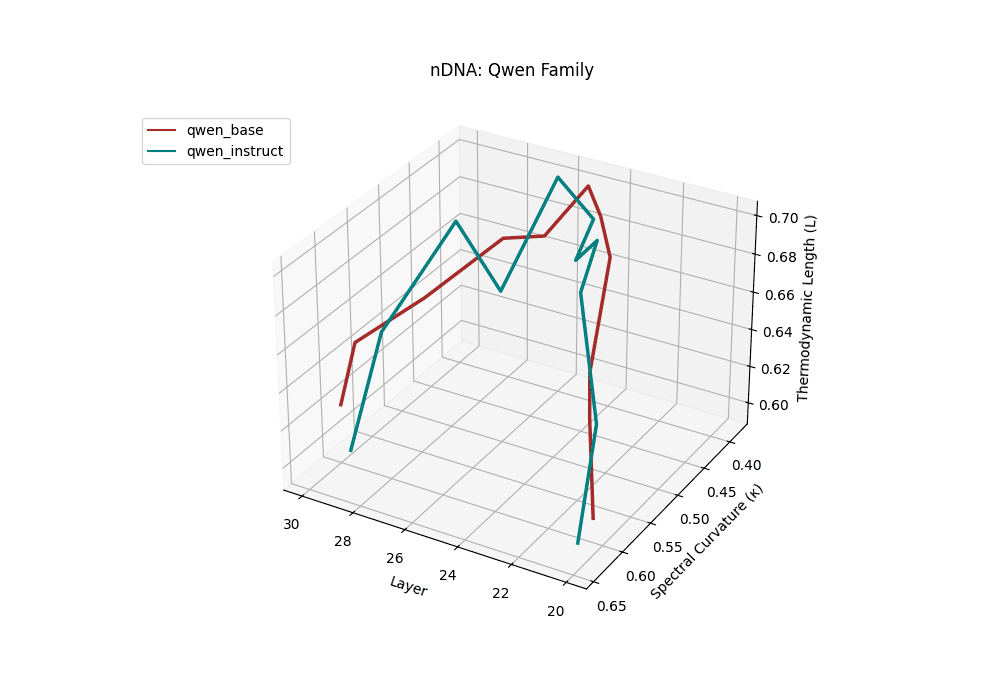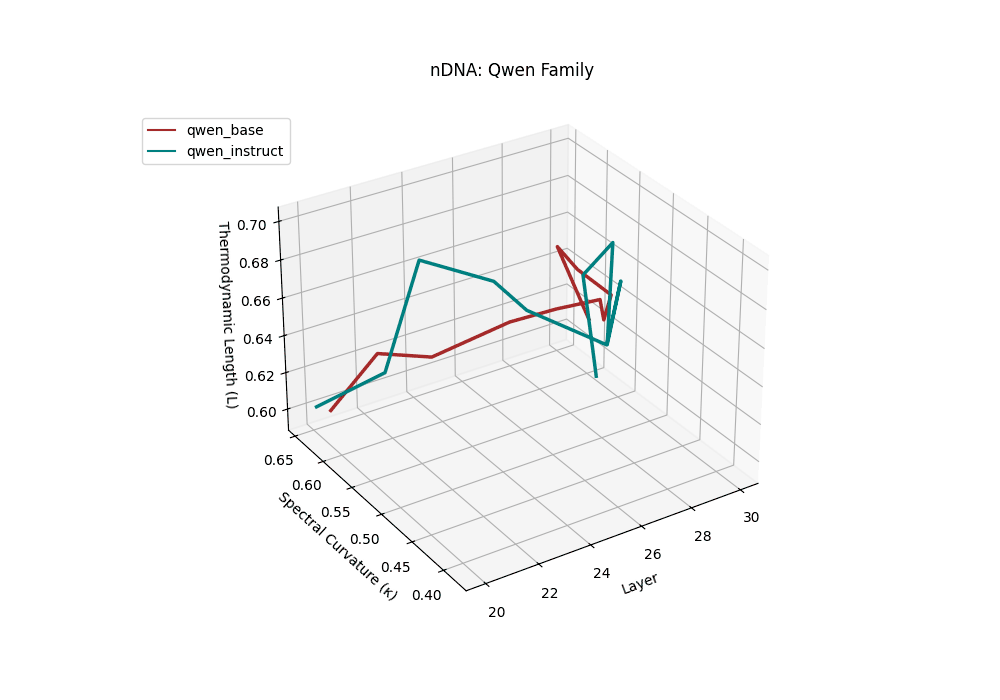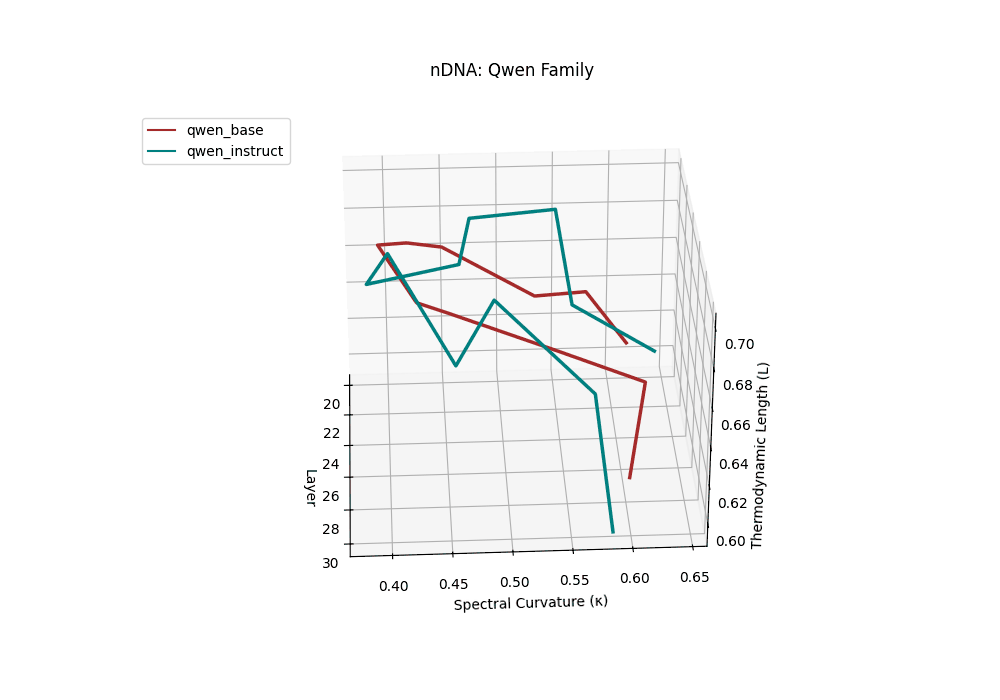
  • Multilingual and culturally calibrated models (e.g., Qwen base/instruct [5])
  • Compact efficient architectures (e.g., Phi-2 [3], TinyLLaMA [3])

These choices reflect contrasting scales [1] [6], pretraining corpora [7], multilingual coverage [5] [8], alignment regimes [9] [10], and distillation strategies [11] [12]. Our goal is to trace how these factors sculpt each model’s nDNA: its unique latent fingerprint of semantic inheritance, epistemic adaptation, and ideological absorption.

Base variants reflect the pretrained backbone: large autoregressive transformers trained on massive corpora for general language modeling objectives. Their latent geometry embodies inherited statistical priors—typically exhibiting smoother spectral curvature (\(\kappa_\ell\)), lower thermodynamic length (\(\mathcal{L}_\ell\)), and minimal directional strain from cultural priors (small \(\|\mathbf{v}_\ell^{(c)}\|\)).

Instruct- and alignment-tuned variants, in contrast, undergo reinforcement learning, instruction fine-tuning, or safety alignment [7] [9]. These models show elevated \(\kappa_\ell\), \(\mathcal{L}_\ell\), and \(\|\mathbf{v}_\ell^{(c)}\|\)—particularly in upper decoder layers—indicating zones of epistemic strain, latent reorientation, and cultural imprinting necessary to align outputs with external value systems.

What we aim to uncover:

  • How alignment and instruction tuning inscribe persistent latent signatures, distinguishing inherited traits from semantic mutations.
  • Whether architectural form (dense vs. MoE) yields distinct geometric adaptation patterns (e.g., localized vs. distributed reconfiguration).
  • Whether compact models preserve latent genomic complexity or collapse toward lower-dimensional manifolds with flattened nDNA signatures.
As shown by the below table from the previous module, this latent geometry is not merely decorative--it is diagnostic.
Layer \(\kappa_\ell\) \(\mathcal{L}_\ell\) \(\|\mathbf{v}_\ell^{(c)}\|\) Belief Vector \(\mathbf{v}_\ell^{(c)}\)
20 0.0412 0.9123 0.6521 [0.1204, -0.0502, 0.0896, ..., 0.0402]
21 0.0458 0.8123 0.7523 [0.1301, -0.0351, 0.0950, ..., 0.0431]
22 0.0523 1.0120 0.5823 [0.1423, -0.0312, 0.0994, ..., 0.0488]
23 0.0581 0.9021 0.6912 [0.1534, 0.0270, 0.1042, ..., 0.0512]
24 0.0639 1.1023 0.5520 [0.1667, 0.0205, 0.1105, ..., 0.0543]
25 0.0505 0.9420 0.8124 [0.1602, -0.0251, 0.1081, ..., 0.0504]
26 0.0398 0.8520 0.6120 [0.1251, 0.0450, 0.0912, ..., 0.0418]
27 0.0512 1.0520 0.7222 [0.1455, -0.0322, 0.1005, ..., 0.0477]
28 0.0590 0.9320 0.5721 [0.1577, 0.0285, 0.1078, ..., 0.0499]
29 0.0672 1.0123 0.6322 [0.1701, -0.0198, 0.1142, ..., 0.0533]
30 0.0555 0.8221 0.7720 [0.1620, -0.0242, 0.1101, ..., 0.0510]
Table 1: An illustrative nDNA example that captures the semantic genome of a foundation model through the joint interplay of spectral curvature (\(\kappa_\ell\)), thermodynamic length (\(\mathcal{L}_\ell\)), and belief vector norm (\(\|\mathbf{v}_\ell^{(c)}\|\)) across layers. Each of these quantities offers a distinct geometric and epistemic lens: \(\kappa_\ell\) measures the local acceleration of latent representations, \(\mathcal{L}_\ell\) quantifies the cumulative internal work required to traverse the belief manifold, while \(\|\mathbf{v}_\ell^{(c)}\|\) encodes the magnitude of cultural drift imposed on latent activations. The color intensities shown alongside each value reflect relative magnitude within column-specific ranges: ■ low, ■ moderate, ■ high, ■ very high. For this example, spectral curvature spans \(\kappa_\ell\) ∈ [0.0400, 0.0700], thermodynamic length \(\mathcal{L}_\ell\) ∈ [0.80, 1.20], and belief vector norm \(\|\mathbf{v}_\ell^{(c)}\|\) ∈ [0.55, 0.75]—revealing regions where the latent manifold bends, epistemic energy intensifies, or external priors steer internal cognition. This triad forms what we term the model's nDNA: a compact, high-dimensional semantic fingerprint that encodes the hidden geometry of belief. It enables us to diagnose zones of inheritance stability, detect ideological absorption, and trace latent mutations introduced by fine-tuning, alignment, or architectural choice. The pattern of these quantities across layers constitutes a signature as unique as a biological genome -- a map of how artificial cognition evolves, remembers, and adapts.

The pattern of \(\mathbf{\kappa_\ell}\), \(\mathbf{\mathcal{L}_\ell}\), and \(\| \mathbf{v}_\ell^{(c)} \|\) across layers reveals:

  • Semantic stability or reorientation: Models that preserve pretrained priors display low curvature and thermodynamic cost across layers [13]. Conversely, instruction-tuned or alignment-heavy models exhibit spikes in curvature and length [7] [8], marking latent restructuring.
  • Zones of cultural pressure: Peaks in belief vector norm \(\| \mathbf{v}_\ell^{(c)} \|\) localize where cultural priors or alignment protocols most strongly steer internal cognition [5] [14].
  • Inheritance fingerprinting: The joint profile of these measures forms a signature–akin to a genomic sequence–allowing us to distinguish, compare, and trace the latent ancestry and adaptation pathways of models [15] [16].

In this sense, nDNA is not a metaphor–it is a geometric genome: an intrinsic latent encoding of how a model thinks, adapts, and inherits. Where biological DNA encodes traits through molecular structure, nDNA encodes them through the curvature, length, and directional flow of latent belief trajectories. This geometry defines not only what the model produces–but how it knows what it knows.

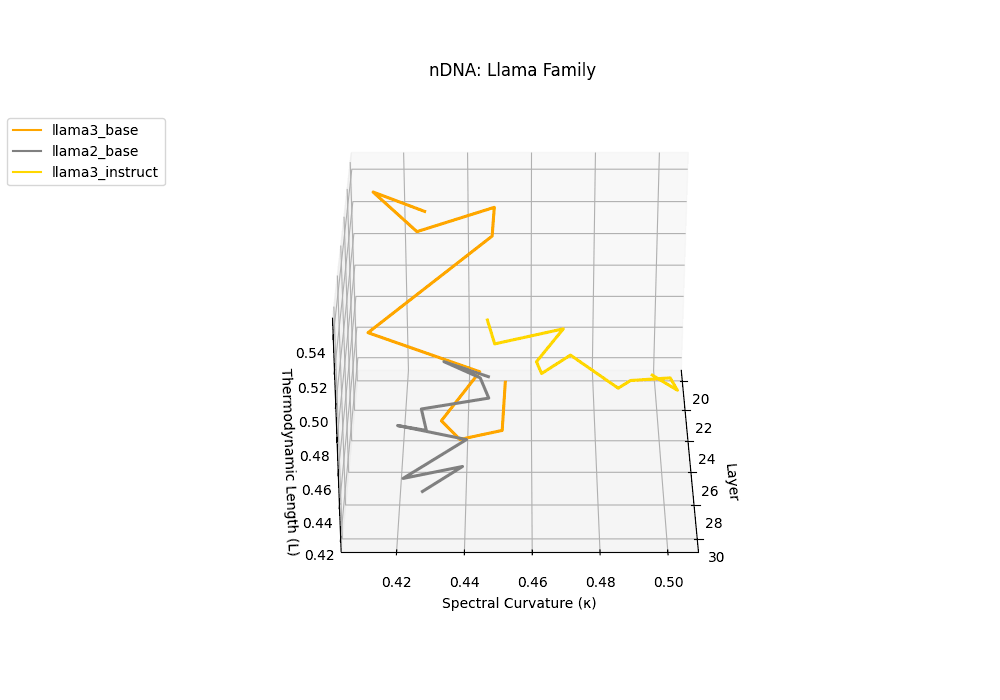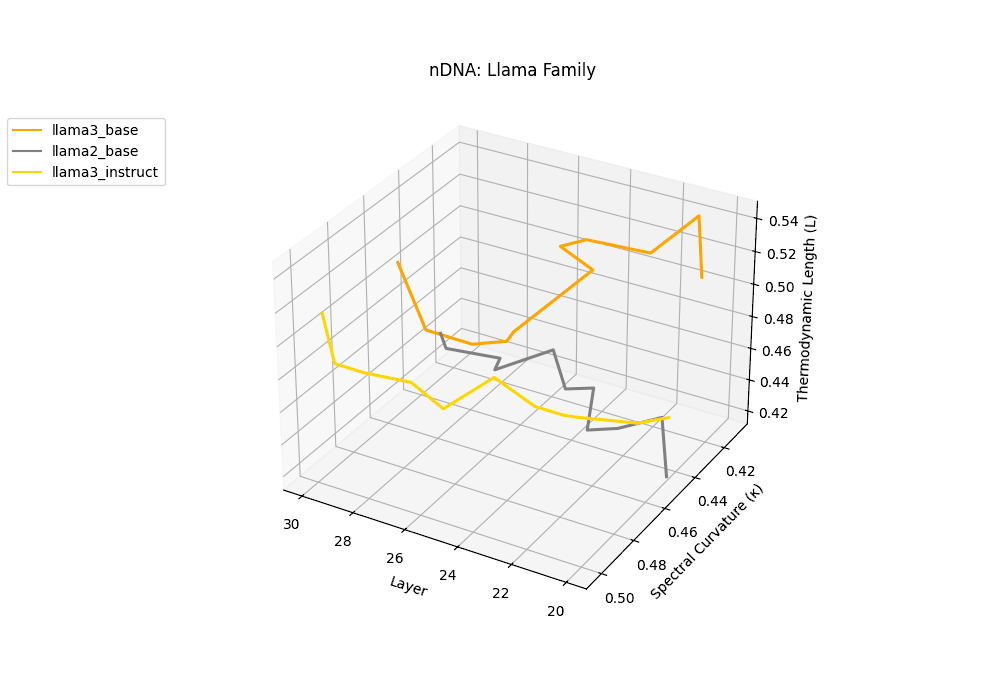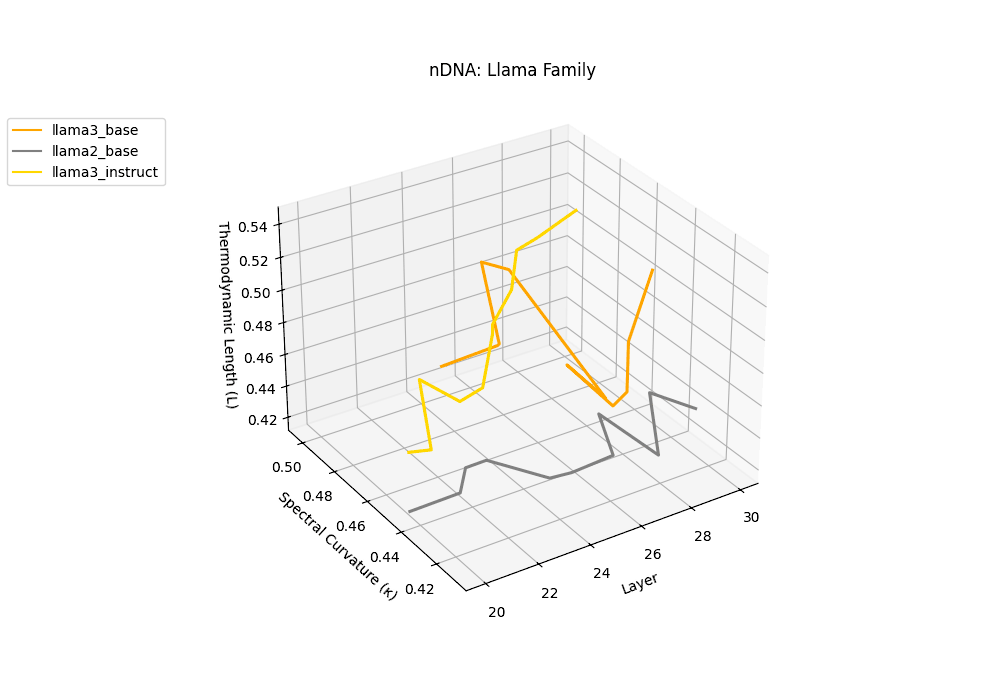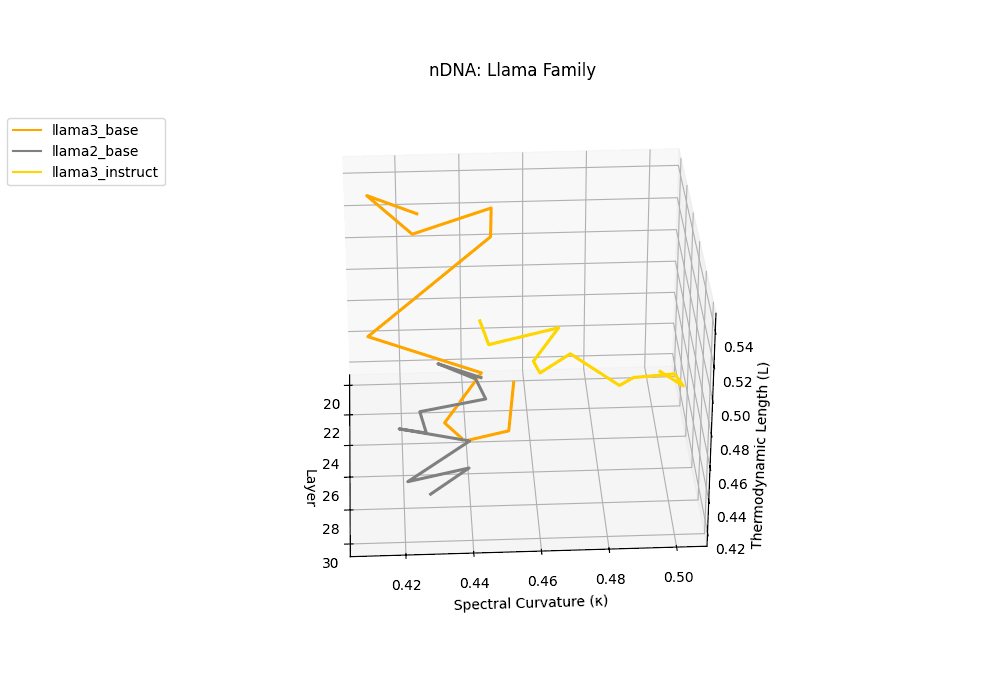
(a) LLaMA Family

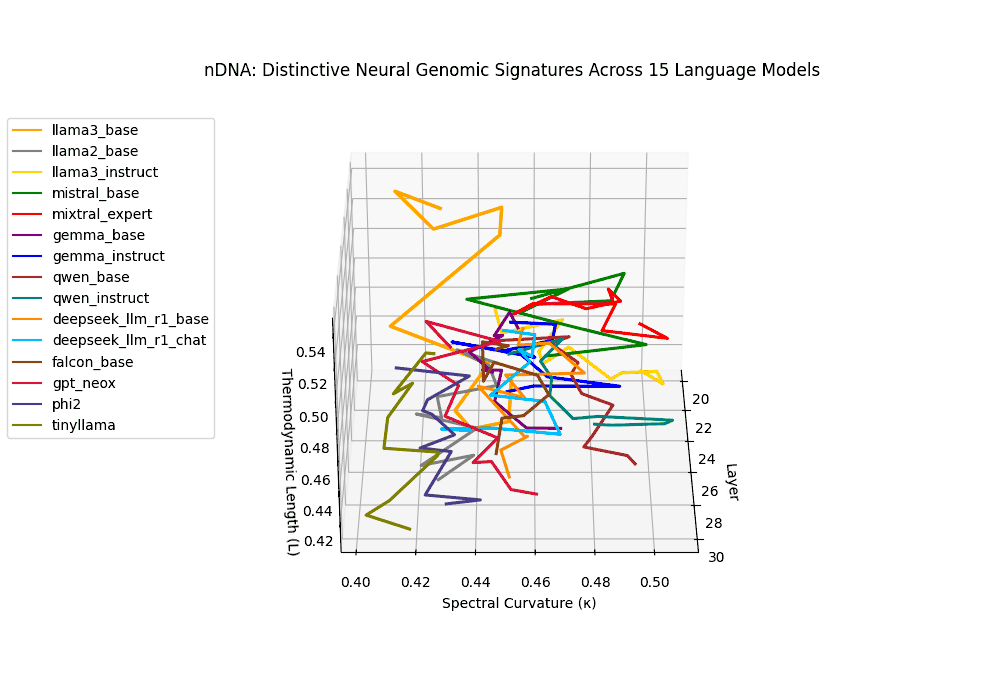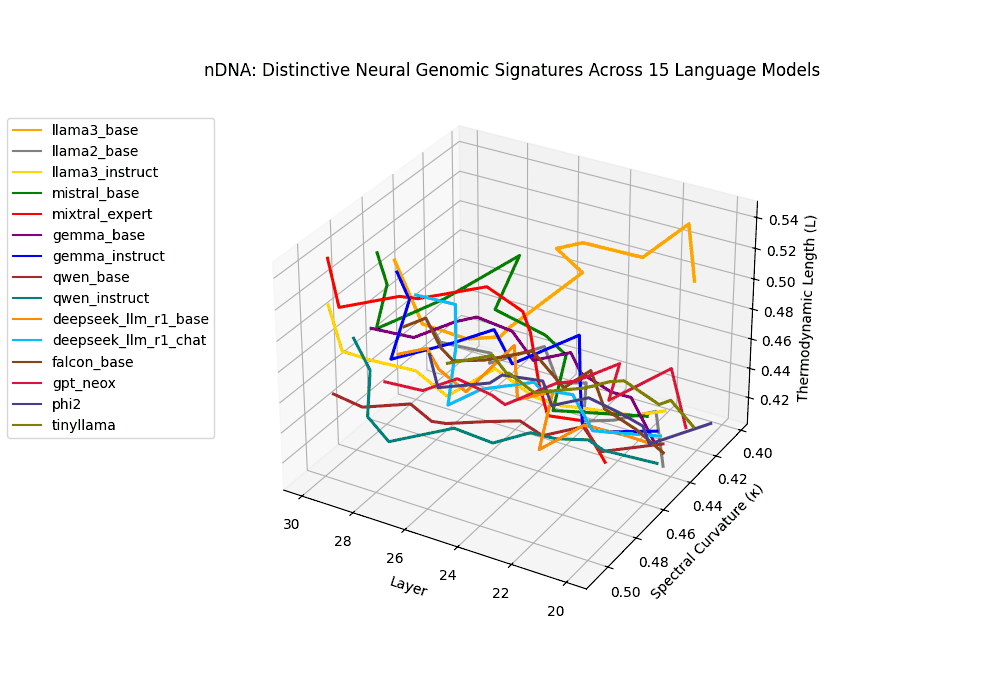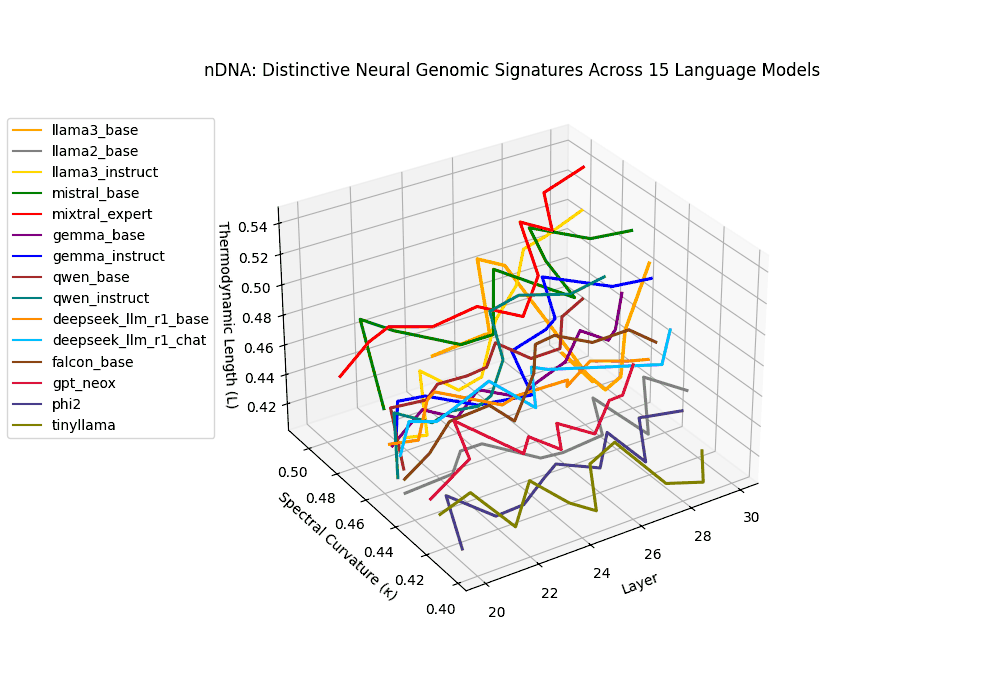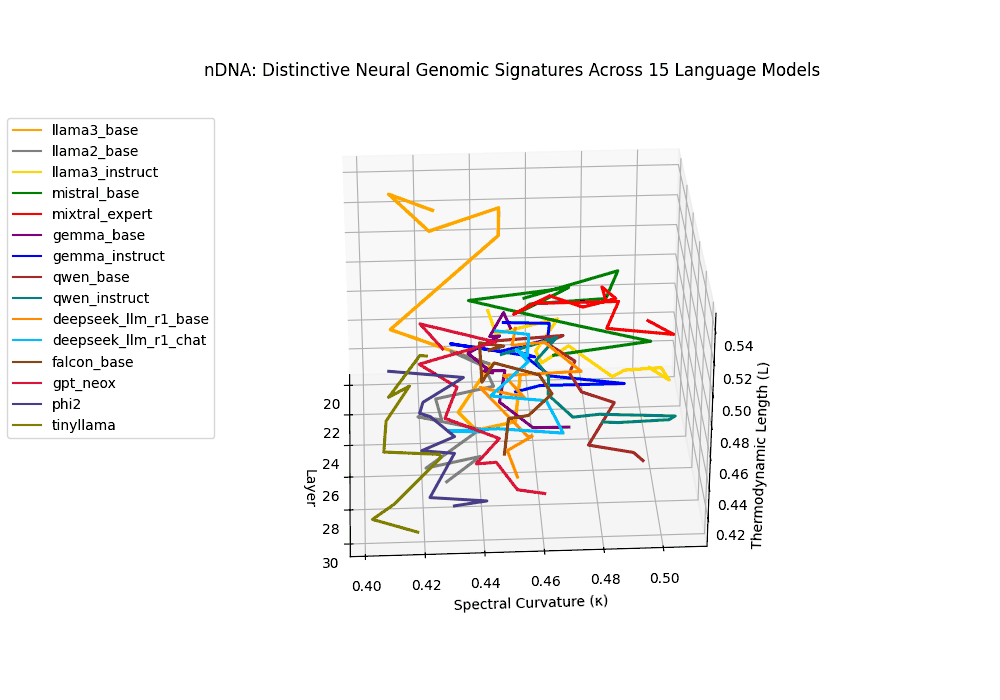
The latent genomic trajectory of LLaMA-3 Instruct displays pronounced spectral curvature rising from \(\kappa_\ell \approx 0.05\) at mid-depth to peaks of \(\kappa_\ell \approx 0.12\) in upper layers (\(\ell \geq 24\)), alongside heightened thermodynamic length increasing from \(\mathcal{L}_\ell \approx 0.8\) to \(\mathcal{L}_\ell \approx 1.3\). This pattern reflects zones of epistemic strain where alignment tuning reshapes internal belief geometry. By contrast, LLaMA-2 and base variants maintain smoother trajectories, with \(\kappa_\ell < 0.04\) and \(\mathcal{L}_\ell < 1.0\), preserving the stability of their pretrained semantic manifold.

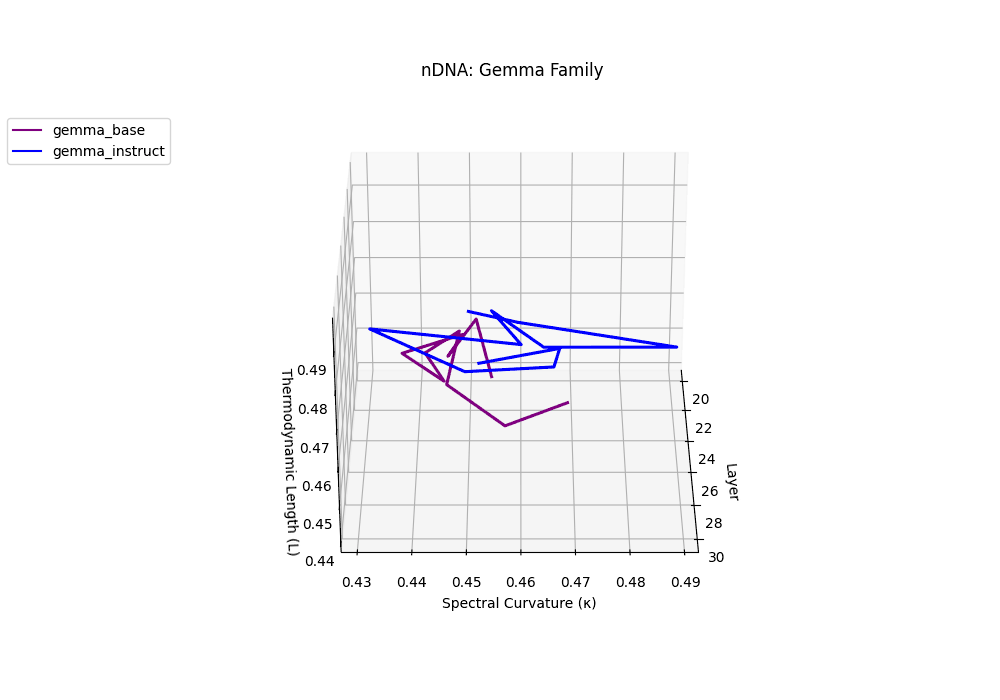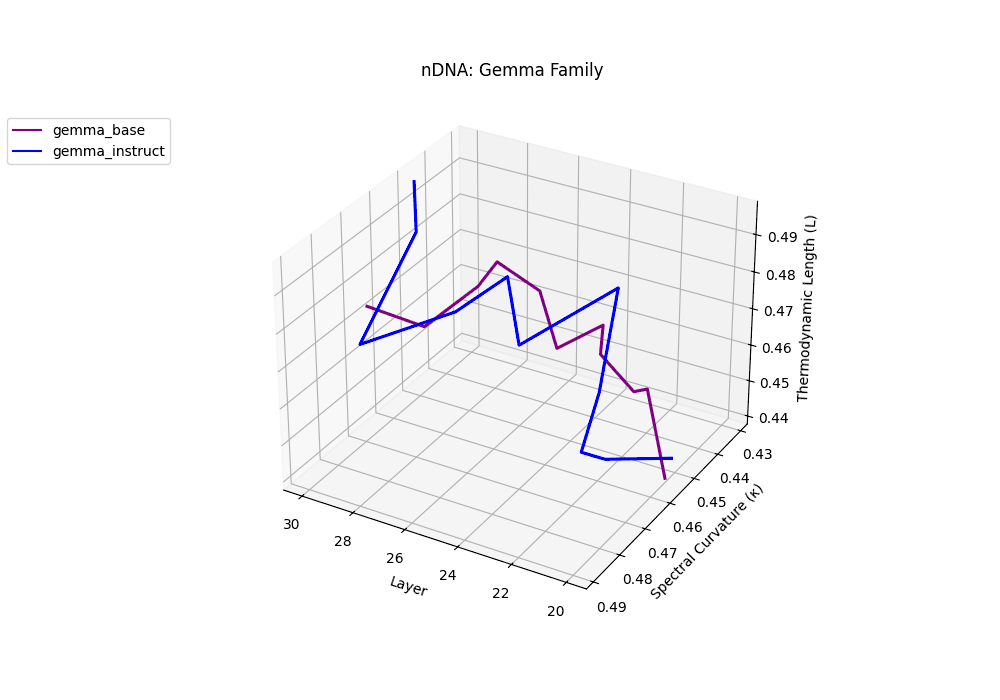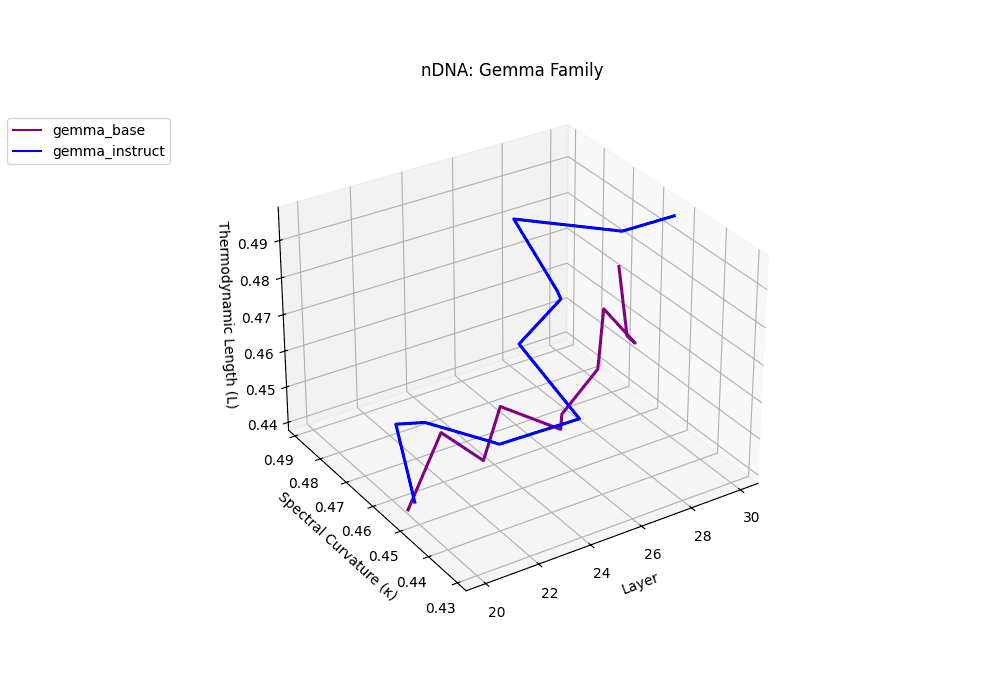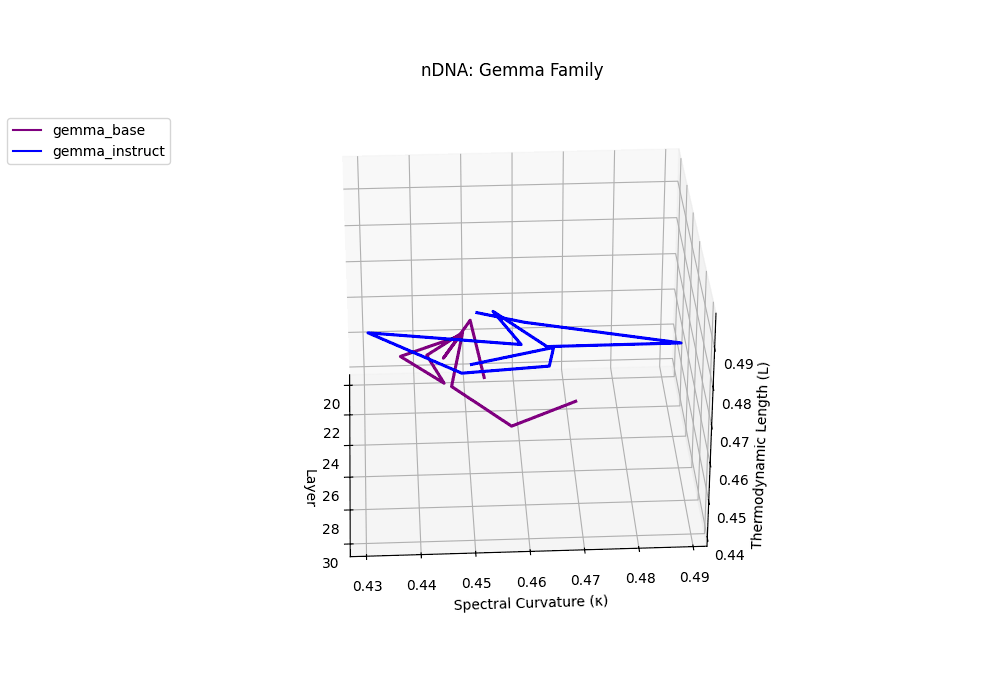
(b) Gemma Family

Gemma Instruct exhibits a noticeable transition in its latent geometry: prior to \(\ell=25\), the spectral curvature stays moderate at \(\kappa_\ell \approx 0.05\), but beyond this point it spikes by 25% to \(\kappa_\ell \approx 0.065\). Similarly, the thermodynamic length rises from \(\mathcal{L}_\ell \approx 1.1\) to peak near \(\mathcal{L}_\ell \approx 1.4\) in the terminal layers. These shifts signal zones of belief reconfiguration where instruction tuning imposes substantial internal adaptation. By contrast, the base variant retains a flatter latent trajectory (\(\kappa_\ell < 0.04\), \(\mathcal{L}_\ell < 1.0\)), reflecting preservation of pretrained semantic structure.

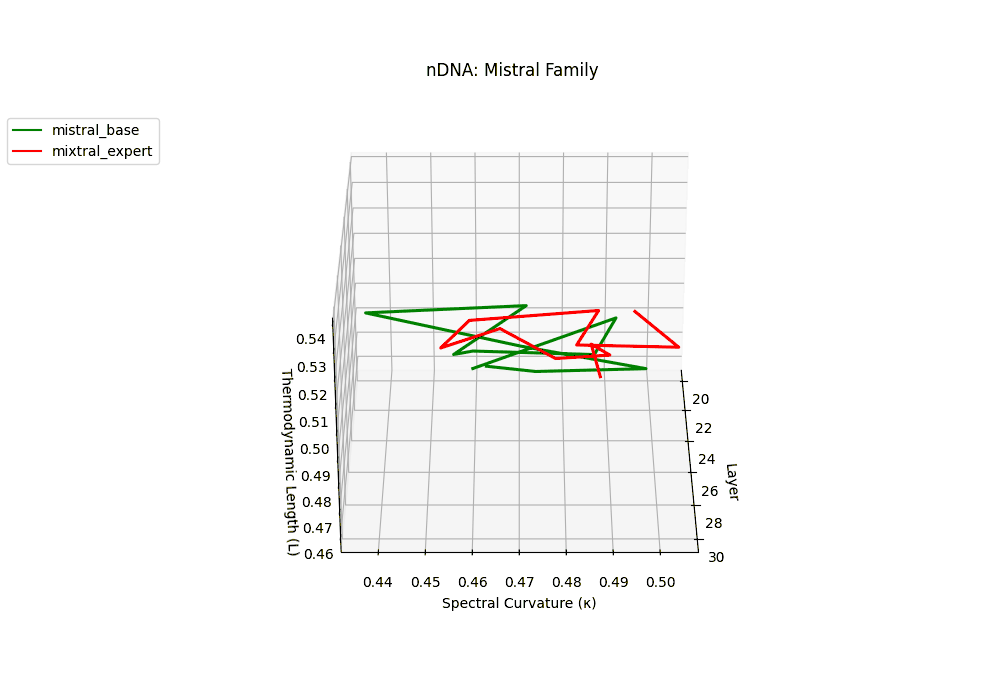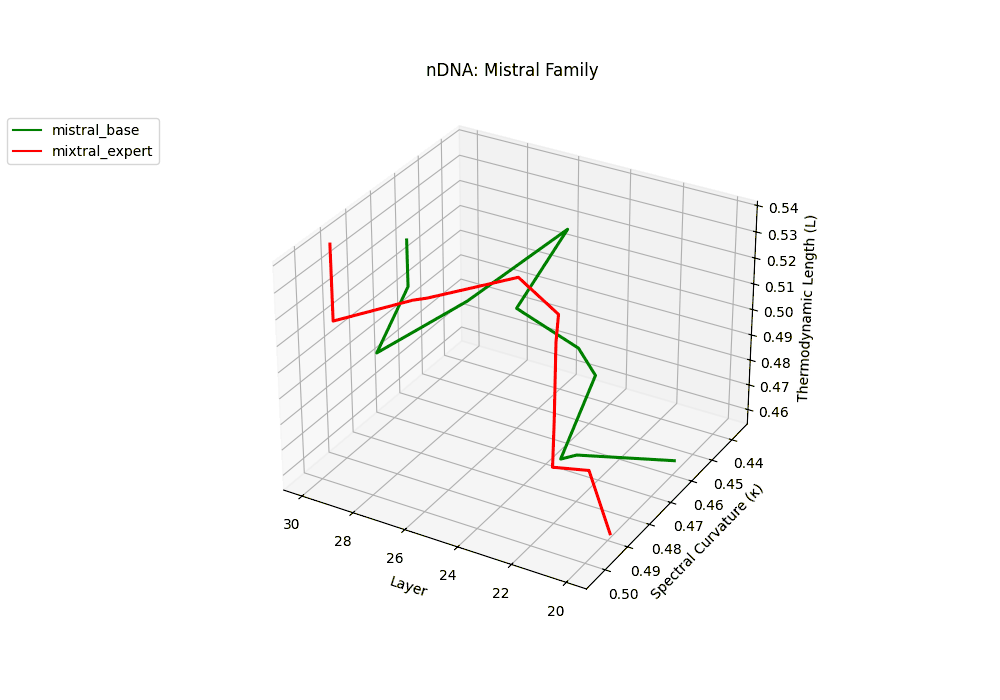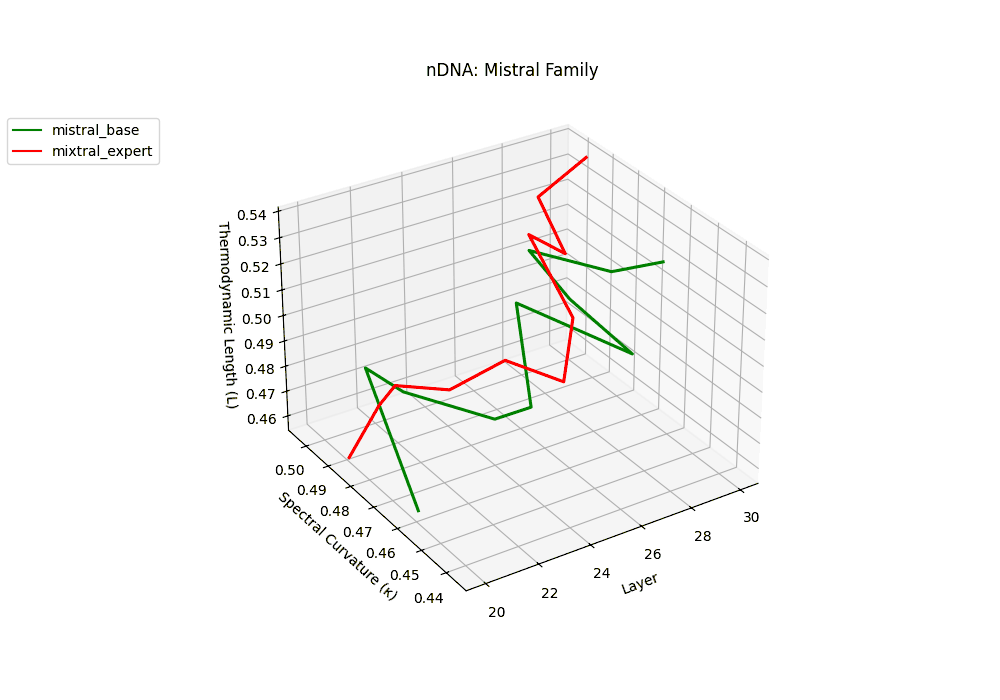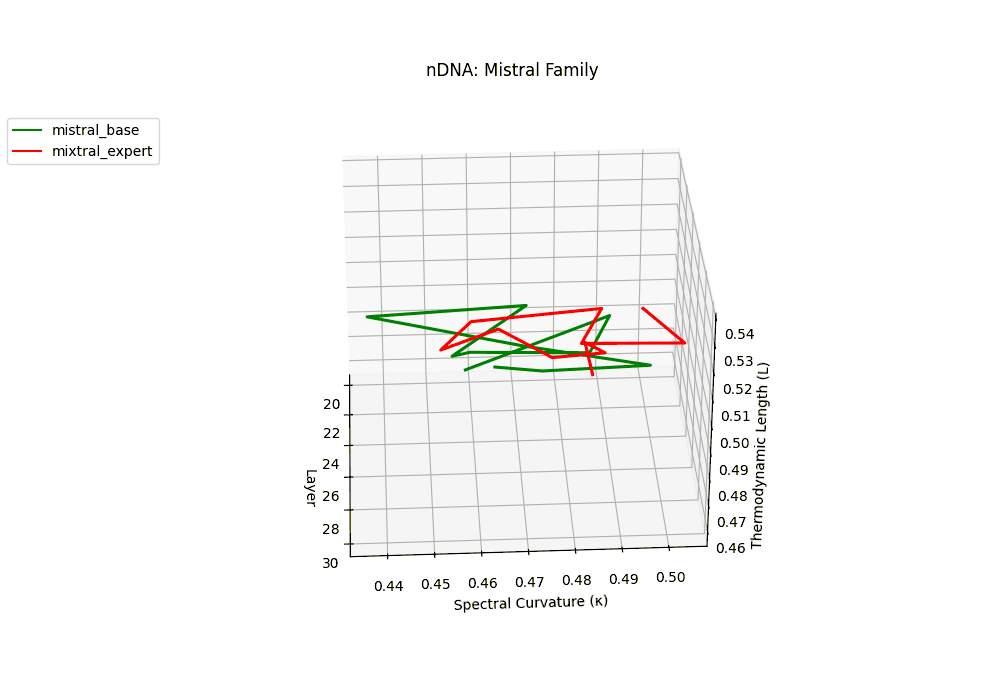
(c) Mistral Family

The Mixtral Expert model exhibits markedly elevated spectral curvature, rising from \(\kappa_\ell \approx 0.05\) in mid layers to peaks near \(\kappa_\ell \approx 0.10\) in routing-active regions (\(\ell \geq 22\)), accompanied by heightened thermodynamic length increasing from \(\mathcal{L}_\ell \approx 0.9\) to \(\mathcal{L}_\ell > 1.1\). These patterns reflect latent specialization driven by expert routing, where different experts selectively reorient and compress pathways in latent space–partitioning conceptual flow and tailoring knowledge representation for efficiency and task-specific precision.

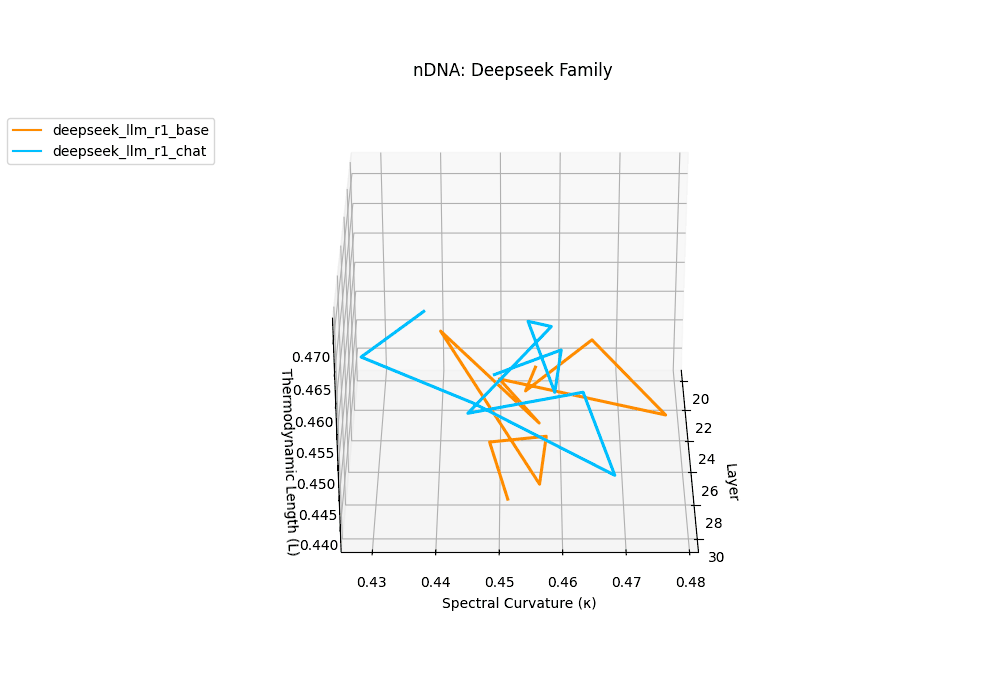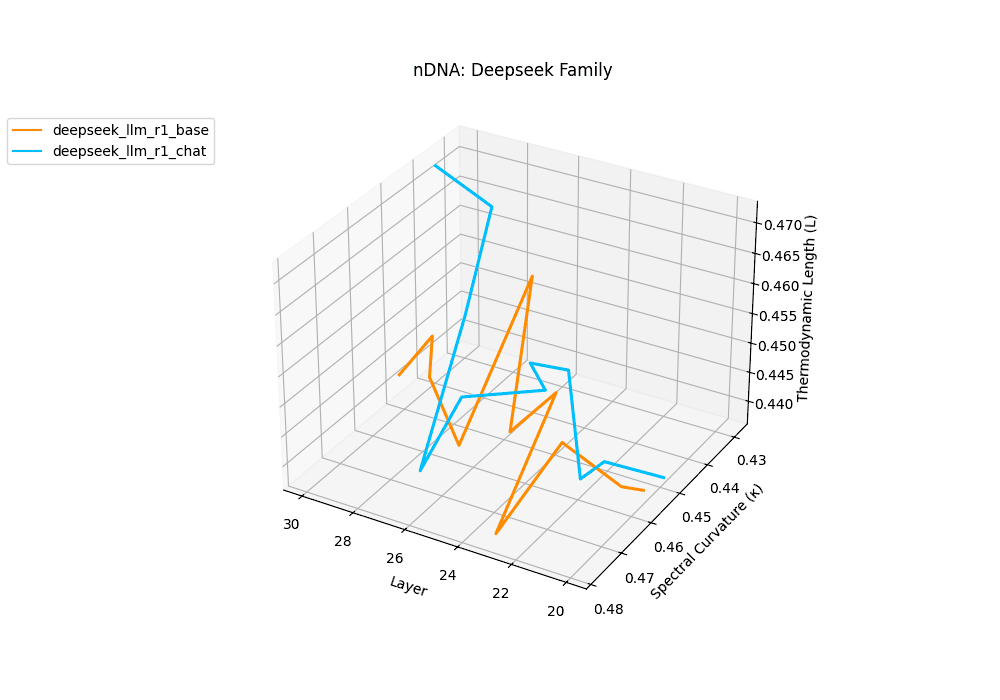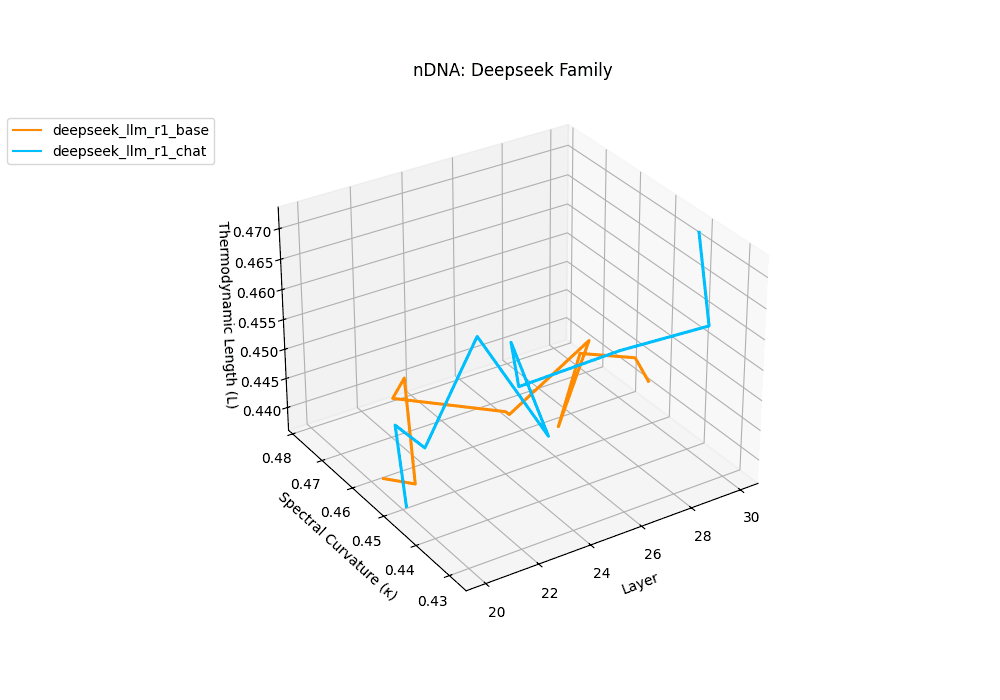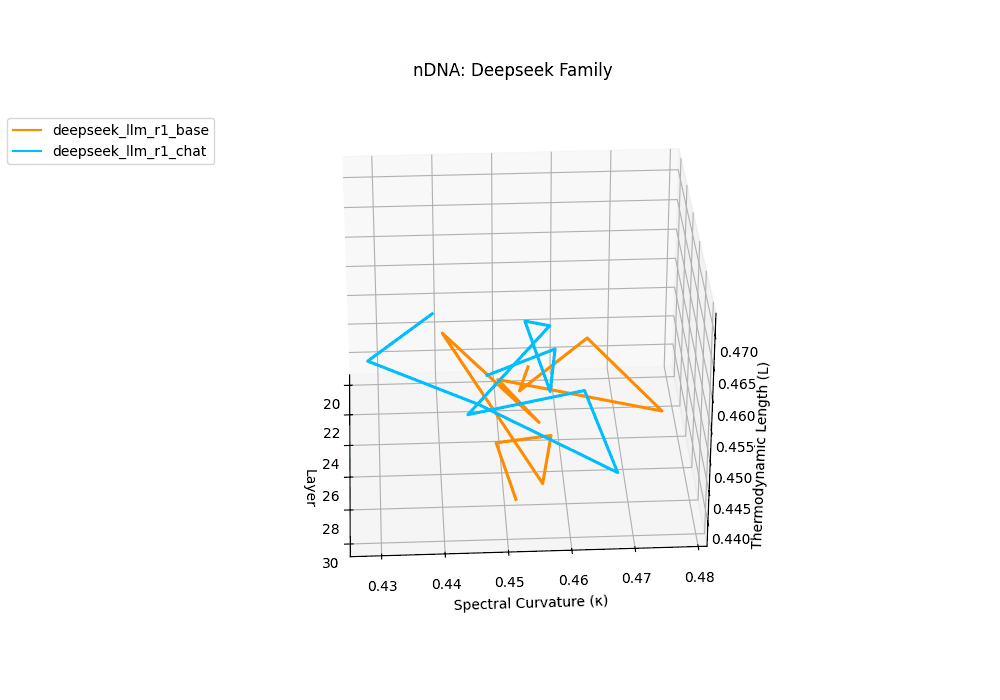
(d) Deepseek Family

The Deepseek Chat variant reveals a steep thermodynamic gradient, with thermodynamic length \(\mathcal{L}_\ell\) increasing from approximately \(0.7\) in mid layers to peaks beyond \(\mathcal{L}_\ell = 1.3\) in upper decoder layers (\(\ell \geq 26\)). Spectral curvature remains moderate (\(\kappa_\ell \leq 0.06\)), indicating that while internal pathways bend gently, the model expends significant epistemic effort to reconcile safety constraints and dialog alignment–reshaping latent beliefs without drastic geometric reorientation.

(e) Qwen Family

Both base and instruct-tuned Qwen models display pronounced latent reorganization, with spectral curvature \(\kappa_\ell\) frequently exceeding \(0.1\) in upper layers (\(\ell \geq 25\)) and thermodynamic length \(\mathcal{L}_\ell\) sustaining elevated levels above \(1.2\) throughout the final decoder blocks. This indicates zones of heightened semantic strain, where the models reconcile multilingual priors with alignment objectives, and areas of ideological absorption, where latent geometry bends under competing cultural and task demands.

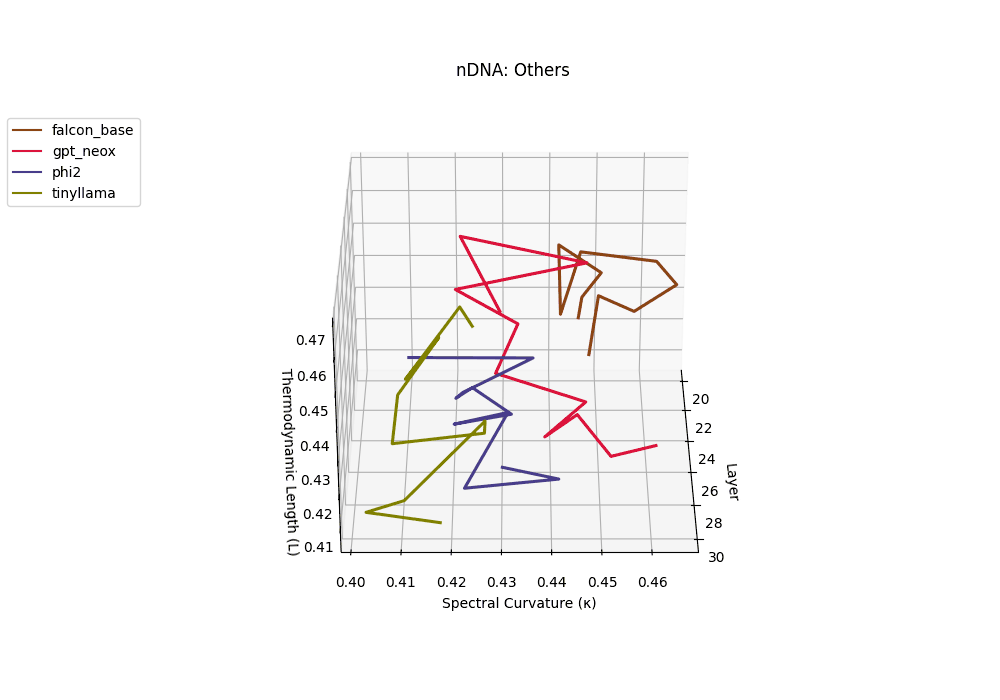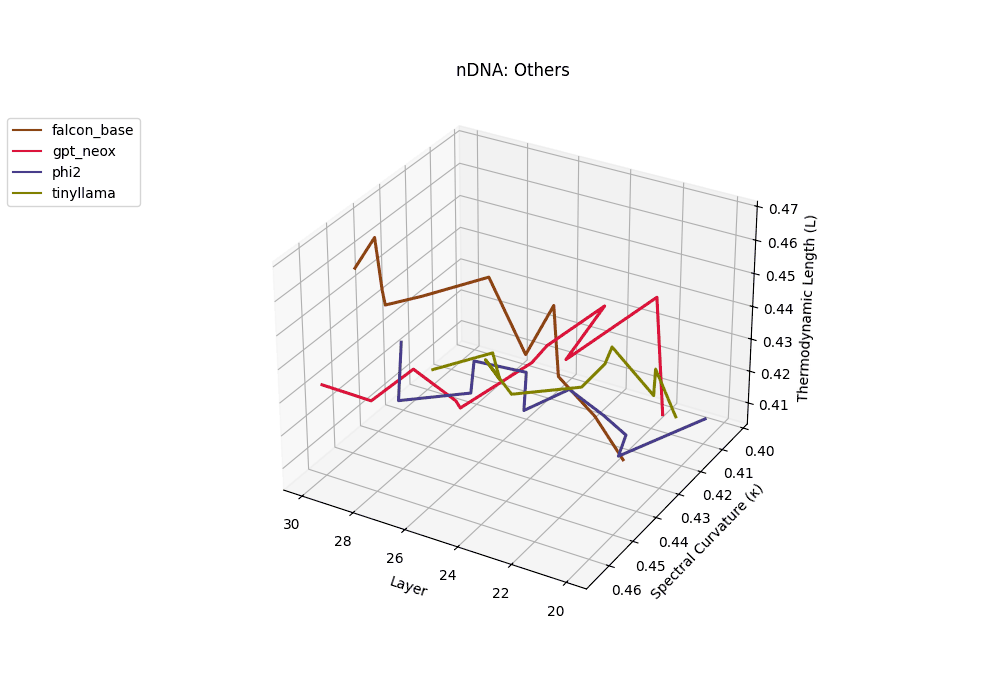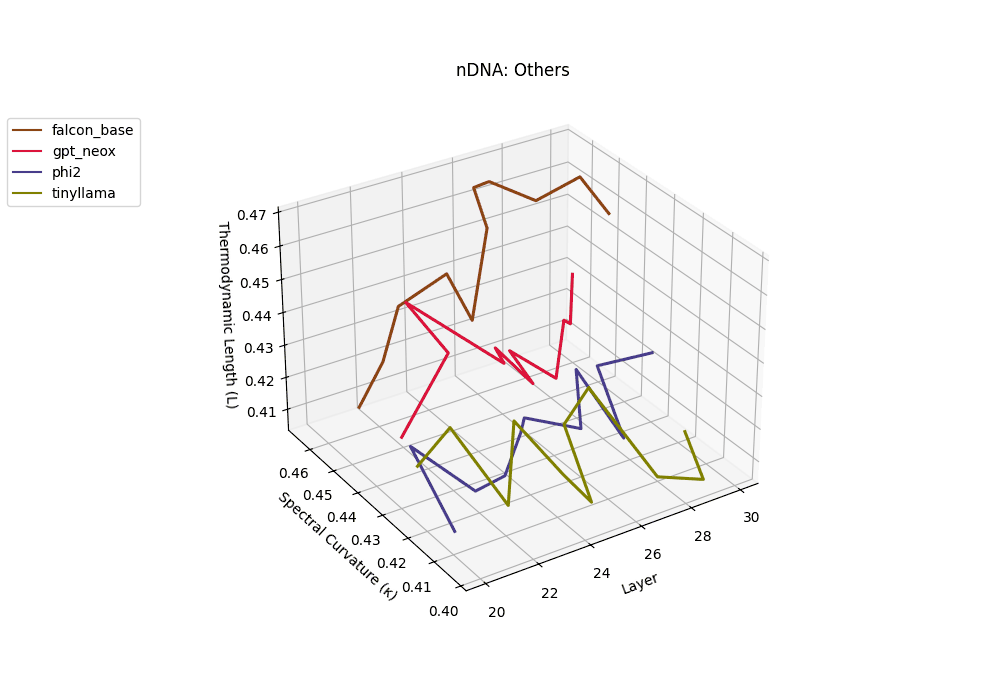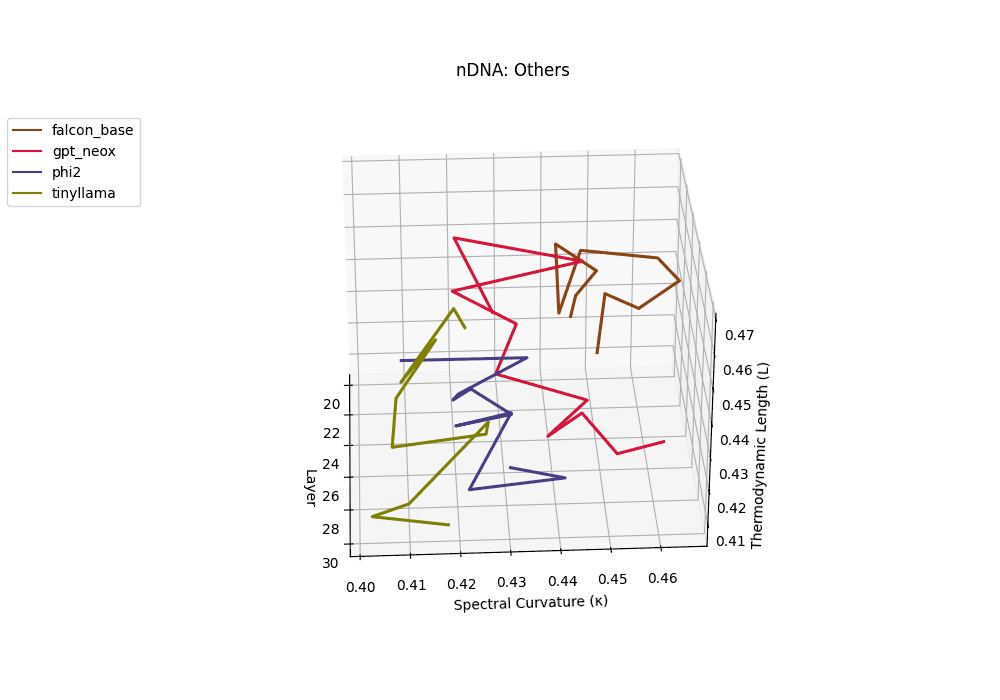
(f) Other Models

Falcon, GPT-NeoX, Phi-2, and TinyLLaMA exhibit notably flatter latent trajectories, with spectral curvature \(\kappa_\ell\) remaining below \(0.03\) and thermodynamic length \(\mathcal{L}_\ell\) consistently under \(0.9\) across layers. This smooth geometry reflects models that largely preserve their pretrained belief structures, undergoing minimal latent reorientation. Such patterns suggest simpler alignment or fine-tuning histories and more conservative design choices that favor stability over aggressive semantic adaptation.

📊 View Interactive Plot
Figure 1: (g) nDNA Landscape across 15 Foundation Models. The composite visualization reveals striking family-level clustering in spectral-thermodynamic space, mapping how foundation models diverge in their latent genomic architecture. High-strain models--notably Qwen and Mixtral--consistently exhibit spectral curvature κℓ exceeding 0.1 and thermodynamic length Lℓ rising beyond 1.2 in upper decoder layers (ℓ ≥ 24). These profiles reflect aggressive latent reorganization driven by multilingual pretraining, expert routing, and intensive alignment adaptation--zones of semantic strain, conceptual shock, and ideological absorption. In contrast, low-strain models such as Falcon, TinyLLaMA, and GPT-NeoX form a distinct cluster where κℓ < 0.03 and Lℓ < 0.9, indicating smoother latent pathways that preserve pretrained epistemic structure with minimal reorientation. LLaMA-3 Instruct, Gemma Instruct, and Deepseek Chat occupy an intermediate zone--showing moderate curvature spikes (κℓ peaking near 0.08) and thermodynamic gradients (Lℓ up to 1.1)--highlighting selective reconfiguration in response to alignment and instruction tuning. This landscape provides a geometric map of neural ancestry and adaptation, illuminating inherited traits, semantic mutations, and the latent genomic signatures that distinguish foundation model families.

Why This Triad? On the Necessity of \(\kappa_\ell\), \(\mathcal{L}_\ell\) and \(\|\mathbf{v}_\ell^{(c)}\|\) for nDNA Geometry

It may be tempting to argue that any pair or triplet of latent metricscould produce seemingly unique latent fingerprints when plotted layer-wise. Why, then, do we assert that the specific triad of spectral curvature (\(\kappa_\ell\)), thermodynamic length (\(\mathcal{L}_\ell\)), and belief vector norm (\(\|\mathbf{v}_\ell^{(c)}\|\)) is both minimal and sufficient for robust nDNA geometry?

Orthogonal yet complementary perspectives on latent dynamics.

Each of the three measures captures a distinct, irreducible axis of the model’s internal epistemic geometry:

  • \(\kappa_\ell\) - The intrinsic semantic curvature of latent trajectories
    • how sharply the internal path of representations bends across depth. It encodes second-order structure, analogous to geometric curvature on manifolds. [17] [18]
  • \(\mathcal{L}_\ell\) - The cumulative epistemic work performed as the model adapts beliefs layer by layer
    • quantifying the energy expenditure needed for belief state transitions in the Fisher–Rao geometry of statistical manifolds. [19] [20] [21]
  • \(\|\mathbf{v}_\ell^{(c)}\|\) - The directional cultural force acting upon the latent manifold
    • how much external priors or sociolinguistic constraints steer internal belief trajectories. [14] [8] [15]

Together, they span latent shape (curvature), internal effort (thermodynamics), and external directional pressure (belief vector field).

Other combinations evaluated and their limitations.

We systematically experimented with numerous alternative metric sets to determine whether they could match or exceed the diagnostic power of this triad:

  • Norm-based pairs: combinations like \((\|h_\ell\|, \|\nabla_\theta h_\ell\|)\), weight norms [22] [23], singular values of attention matrices [24], these collapse under trivial rescaling and layer normalization [25], offering little insight into geometric inflections or external directional forces. They reflect magnitude, not structure.
  • Gradient-only diagnostics: Fisher information diagonal [26] [27], local logit gradients [28], these capture internal strain or sensitivity but fail to reveal latent manifold curvature or the directional drift imposed by external priors, leaving cultural or alignment effects hidden.
  • Entropy measures: activation entropy [29], token probability entropy [30], valuable for quantifying output uncertainty or diversity, but disconnected from the internal geometric dynamics that govern latent inheritance or reorganization.
  • Pairings of curvature and local statistics: attempts like (\(\kappa_\ell\), activation variance) [31], (\(\mathcal{L}_\ell\), ‖hₗ‖) fail to jointly encode latent shape, adaptation cost, and directional drift in a unified, interpretable manner. They fragment geometric, energetic, and external-force insights rather than synthesizing them.

None of these alternatives provided the geometric separability across model families (e.g., LLaMA vs. Mixtral vs. Qwen) nor the interpretability of zones of mutation, inheritance, and adaptation that our triad achieved.

Effectiveness in revealing hidden geometry.

What ultimately validates this triad is its empirical effectiveness in unveiling the hidden structural signatures of:

  • Finetuning and alignment: zones where latent paths sharply reorient and effort spikes, e.g., LLaMA-3 Instruct vs. LLaMA-2 base [1] [2].
  • Cultural calibration: regions where \(\|\mathbf{v}_\ell^{(c)}\|\) reveals external value steering, e.g., Qwen instruct’s ideological absorption [5].
  • Architectural specialization: how MoE models like Mixtral partition latent space via curvature and effort redistribution [3].
  • Collapse and merging: detection of flattening or hybridization of latent manifolds in model collapse and neural marriages [14] [12].

These are phenomena we rigorously map in the sections that follow, each tied to distinctive nDNA signatures visible only when these three axes are combined.

Why not more metrics? Why not fewer?

Adding further dimensions (e.g., activation norms, entropy, variance) increased noise and reduced interpretability, without providing meaningful new axes of latent epistemic variation. Reducing to two metrics (e.g., \(\kappa_\ell\) and \(\mathcal{L}_\ell\)) failed to localize external cultural or alignment forces. The triad represents the minimal sufficient grammar to capture inheritance dynamics, as validated in Table 1 and Figure 1.

Summary

The nDNA triad provides a latent genomic coordinate system:

\[\boxed{ \underbrace{\text{Intrinsic curvature}}_{\kappa_\ell} \quad + \quad \underbrace{\text{Epistemic effort}}_{\mathcal{L}_\ell} \quad + \quad \underbrace{\text{External steering}}_{\|\mathbf{v}_\ell^{(c)}\|} \quad \Rightarrow \quad \text{nDNA: a unique fingerprint of neural inheritance.}}\]

Its power lies not only in theoretical soundness [21] [17], but in its empirical capacity to disentangle inherited traits, zones of mutation, and ideological drift that no arbitrary metric combination could replicate.

While belief vectors are the core focus, one could consider extending to belief tensors for richer representation; however, this would significantly increase computational cost and complexity.

References

[1] Touvron, Hugo and Others “LLaMA: Open and efficient foundation language models” arXiv preprint arXiv:2302.13971 (2023).

[2] Dubey, Abhimanyu, Jauhri, Abhinav, and others “The Llama 3 Herd of Models” arXiv:2407.21783 (2024). https://arxiv.org/abs/2407.21783

[3] Bommasani, R. and others “Foundation models: Past, present, and future” arXiv preprint arXiv:2309.00616 (2023).

[4] Sid Black, Stella Biderman, and others “GPT-NeoX-20B: An Open-Source Autoregressive Language Model” arXiv:2204.06745 (2022). https://arxiv.org/abs/2204.06745

[5] Peng, Baolin, Wang, Li, and others “Culturally aligned language modeling: Methods and benchmarks” ACL (2024).

[6] OpenLM contributors “DeepSeek LLMs: Bridging Open Pre-training and Alignment” arXiv preprint arXiv:2312.00764 (2023).

[7] Bai, Yuntao and others “Constitutional AI: Harmlessness from AI Feedback” arXiv preprint arXiv:2212.08073 (2023).

[8] Zhou, Ben and others “On Alignment Drift in Large Language Models” arXiv preprint arXiv:2310.02979 (2023).

[9] Laurens, Ethan and others “The Ethics of Alignment: Towards Culturally Inclusive Foundation Models” Proceedings of the AAAI Conference on Artificial Intelligence (2024).

[10] Ganguli, Deep and others “Reducing sycophancy in large language models via self-distillation” arXiv preprint arXiv:2305.17493 (2023).

[11] Wu, Z. and others “Seamless: Robust distillation of large models” ICML (2024).

[12] Xu, J. and others “Aligning large language models with iterative feedback” ICLR (2023).

[13] Liu, Nelson and others “Hidden Progress in Language Models” arXiv preprint arXiv:2305.04388 (2023).

[14] Wang, Ziwei, Xu, Yichao, and others “Cultural bias in large language models: A survey” arXiv preprint arXiv:2311.05691 (2023).

[15] Shen, Sheng and others “The Geometry of Belief in Language Models” arXiv preprint arXiv:2305.12355 (2023).

[16] Bakker, Tom and others “Uniting Model Merging and Distillation: Towards Unified Neural Inheritance” arXiv preprint arXiv:2402.00999 (2024).

[17] Farzam, Amir, Subramani, Akshay, and others “Ricci Curvature Reveals Alignment Dynamics in Language Models” ICLR (2024).

[18] Xu, Yifan and Tong, Hanghang “Spherical Graph Neural Networks for Learning on Non-Euclidean Structures” ICLR (2022).

[19] Crooks, Gavin E “Measuring thermodynamic length” Physical Review Letters (2007).

[20] Wagner, Henrik and Bubeck, Sébastien “Thermodynamic Metrics Reveal Capacity Allocation in Transformers” arXiv preprint arXiv:2306.13052 (2023).

[21] Amari, Shun-ichi “Information geometry and its applications” Applied Mathematical Sciences (2016).

[22] Neyshabur, Behnam, Tomioka, Ryota, and others “Norm-based capacity control in neural networks” COLT (2015).

[23] Zhang, Hongyi, Dauphin, Yann N, and others “All you need is a good init” ICLR (2019).

[24] Gao, Pengfei, Huang, Xiaobo, and others “Representation degeneration problem in training deep neural networks” ICLR (2019).

[25] Ba, Jimmy Lei, Kiros, Jamie Ryan, and others “Layer normalization” arXiv preprint arXiv:1607.06450 (2016).

[26] Amari, Shun-ichi “Natural gradient works efficiently in learning” Neural Computation (1998).

[27] Kunstner, Frederik, Balles, Lukas, and others “Limitations of the empirical Fisher approximation for natural gradient descent” NeurIPS (2019).

[28] Ji, Yujia, Lipton, Zachary C, and others “Directional analysis of the fine-tuning dynamics of pre-trained transformers” ACL (2020).

[29] Belinkov, Yonatan and Glass, James “Analyzing the stability of neural models for sequence tagging” EMNLP (2017).

[30] Mielke, Sabrina J., Eisenschlos, Julian, and others “Between minds and machines: Measuring language models’ consistency with human knowledge” ACL (2021).

[31] Raghu, Maithra, Gilmer, Justin, and others “SVCCA: Singular vector canonical correlation analysis for deep learning dynamics and interpretability” NeurIPS (2017).